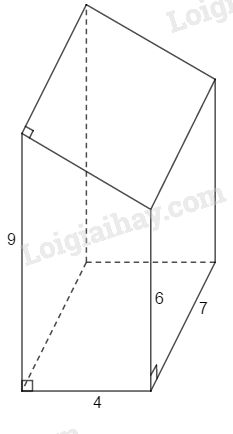
Bài 42 trang 144 SBT toán 8 tập 2Giải bài 42 trang 144 sách bài tập toán 8. Diện tích toàn phần của hình lăng trụ đứng, tính theo các kích thước đã cho trên hình 131 ... Đề bài Diện tích toàn phần của hình lăng trụ đứng, tính theo các kích thước đã cho trên hình \(131\) là:
A. \(228\) B. \(240\) C. \(196\) D. \(170\) E. \(210.\) Hãy chọn kết quả đúng. Phương pháp giải - Xem chi tiết Sử dụng: - Diện tích xung quanh của hình lăng trụ đứng bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao. \({S_{xq}} = 2p.h\) Trong đó: \(p\) là nửa chu vi đáy, \(h\) là chiều cao. - Diện tích toàn phần của hình lăng trụ bằng tổng diện tích xung quanh và diện tích hai đáy. Lời giải chi tiết
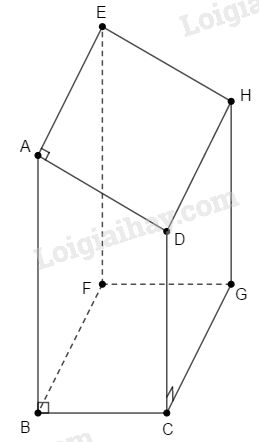
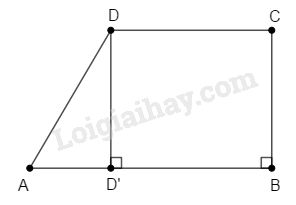
Xét hình thang \(ABCD\), dựng đường cao \(DD'\).
Tứ giác \(DCBD'\) có \(BD'//DC\) và \(DD'//BC\) (do cùng vuông góc với AB) nên \(DCBD'\) là hình bình hành Nên \(BD'=DC=6cm\) Do đó, \(AD'=AB-BD'=9-6=3\) (đơn vị độ dài). Áp dụng định lí Pytago vào tam giác vuông \(ADD'\), ta có: \(A{D^2} = AD{'^2} + DD{'^2}\) \(\Rightarrow AD = \sqrt {{3^2} + {4^2}} = 5\,\) (đơn vị độ dài) Diện tích xung quanh của hình lăng trụ là: \({S_{xq}} = \left( {AB + BC + CD + DA} \right).CG\) \(= \left( {9 + 4 + 6 + 5} \right).7 = 168\) (đơn vị diện tích) Diện tích một mặt đáy hình lăng trụ là: \({S_đ} = \dfrac{1}{2}\left( {AB + CD} \right).CB \)\(\,= \dfrac{1}{2}.\left( {9 + 6} \right).4 = 30\) (đơn vị diện tích). Diện tích toàn phần của hình lăng trụ là: \({S_{TP}} = {S_{xq}} + 2{S_d} = 168 + 2.30 = 228\) (đơn vị diện tích). Chọn A. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
