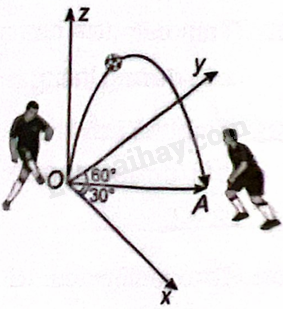
Giải bài 39 trang 54 sách bài tập toán 12 - Kết nối tri thứcMột quả bóng được chuyền theo một đường parabol nằm trong một mặt phẳng (left( alpha right)) vuông góc với mặt sân cỏ, từ vị trí O đến vị trí A cách O một khoảng 20 m về hướng (S{30^ circ }E) (hướng tạo với hướng nam góc ({30^ circ }) và tạo với hướng đông góc ({60^ circ })). Các vị trí O, A đều thuộc sân cỏ. Chọn hệ trục tọa độ Oxyz có gốc tại điểm O, các trục Ox, Oy thuộc mặt sân cỏ (phẳng), tia Ox chỉ hướng nam, tia Oy chỉ hướng đông, đơn vị đo theo mét. Viết phương trình mặt p Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Một quả bóng được chuyền theo một đường parabol nằm trong một mặt phẳng \(\left( \alpha \right)\) vuông góc với mặt sân cỏ, từ vị trí O đến vị trí A cách O một khoảng 20 m về hướng \(S{30^ \circ }E\) (hướng tạo với hướng nam góc \({30^ \circ }\) và tạo với hướng đông góc \({60^ \circ }\)). Các vị trí O, A đều thuộc sân cỏ. Chọn hệ trục tọa độ Oxyz có gốc tại điểm O, các trục Ox, Oy thuộc mặt sân cỏ (phẳng), tia Ox chỉ hướng nam, tia Oy chỉ hướng đông, đơn vị đo theo mét. Viết phương trình mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải - Xem chi tiết Xác định tọa độ điểm A. Mặt phẳng \(\left( \alpha \right)\) là mặt phẳng chứa \(OA\) và trục \(Oz\). Lời giải chi tiết Ta có \(OA = 20m\) nên \(\left\{ \begin{array}{l}{x_A} = OA \cdot \cos {30^ \circ } = 10\\{y_A} = OA \cdot \cos {60^ \circ } = 10\sqrt 3 \\{z_A} = 0\end{array} \right.\), tức là \(A\left( {10;10\sqrt 3 ;0} \right)\). Suy ra \(\overrightarrow {OA} = \left( {10;10\sqrt 3 ;0} \right)\). Mặt phẳng \(\left( \alpha \right)\) là mặt phẳng chứa \(OA\) và trục \(Oz\). Trục \(Oz\) có vectơ chỉ phương là \(\overrightarrow k = \left( {0;0;1} \right) \Rightarrow \overrightarrow n = \left[ {\overrightarrow {OA} ,\overrightarrow k } \right] = 10\left( {\sqrt 3 ; - 1;0} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\). Phương trình mặt phẳng \(\left( \alpha \right)\) là \(\left( \alpha \right):\sqrt 3 \left( {x - 0} \right) - 1\left( {y - 0} \right) + 0\left( {z - 0} \right) = 0 \Leftrightarrow \sqrt 3 x - y = 0\).
|