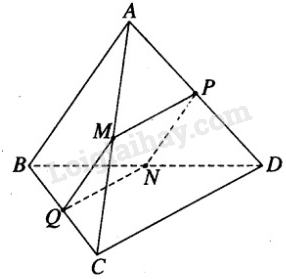
Bài 3.7 trang 103 SBT hình học 12

Đề bài

Cho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng:

a) $\overrightarrow {AB}  + \overrightarrow {CD}  = \overrightarrow {AD}  + \overrightarrow {CB}  = 2\overrightarrow {MN}$

b) $\overrightarrow {AB}  - \overrightarrow {CD}  = \overrightarrow {AC}  - \overrightarrow {BD}  = 2\overrightarrow {PQ}$

Lời giải chi tiết

a) Ta có  MPNQ là hình bình hành vì  $\overrightarrow {MP}  = \overrightarrow {QN}  = \dfrac{1}{2}\overrightarrow {CD}$ và $\overrightarrow {MQ}  = \overrightarrow {PN}  = \dfrac{1}{2}\overrightarrow {AB}$.

Do đó  $\overrightarrow {MN}  = \overrightarrow {MQ}  + \overrightarrow {MP}  = \dfrac{{\overrightarrow {AB} }}{2} + \dfrac{{\overrightarrow {CD} }}{2}$  hay  $2\overrightarrow {MN}  = \overrightarrow {AB}  + \overrightarrow {CD}$      (1)

Mặt khác  $\overrightarrow {AB}  = \overrightarrow {AD}  + \overrightarrow {DB}$

$\overrightarrow {CD}  = \overrightarrow {CB}  + \overrightarrow {BD}$

Nên  $\overrightarrow {AB}  + \overrightarrow {CD}  = \overrightarrow {AD}  + \overrightarrow {CB}$           (2)

Vì $\overrightarrow {DB}  =  - \overrightarrow {BD}$

Từ (1) và (2) ta có: $\overrightarrow {AB}  + \overrightarrow {CD}  = \overrightarrow {AD}  + \overrightarrow {CB}  = 2\overrightarrow {MN}$  là đẳng thức cần chứng minh.

b) Ta có: $\overrightarrow {PQ}  = \overrightarrow {MQ}  - \overrightarrow {MP}  = \dfrac{{\overrightarrow {AB} }}{2} - \dfrac{{\overrightarrow {CD} }}{2}$

Do đó:  $2\overrightarrow {PQ}  = \overrightarrow {AB}  - \overrightarrow {CD}$        (3)

Mặt khác:  $\overrightarrow {AB}  = \overrightarrow {AC}  + \overrightarrow {CB}$

$\overrightarrow {CD}  = \overrightarrow {BD}  - \overrightarrow {BC}$

Nên $\overrightarrow {AB}  - \overrightarrow {CD}  = \overrightarrow {AC}  - \overrightarrow {BD}$             (4)

Vì  $\overrightarrow {CB}  - ( - \overrightarrow {BC} ) = \overrightarrow 0$

Từ (3) và (4) ta suy ra  $\overrightarrow {AB}  - \overrightarrow {CD}  = \overrightarrow {AC}  - \overrightarrow {BD}  = 2\overrightarrow {PQ}$ là đẳng thức cần chứng minh.

HocTot.Nam.Name.Vn