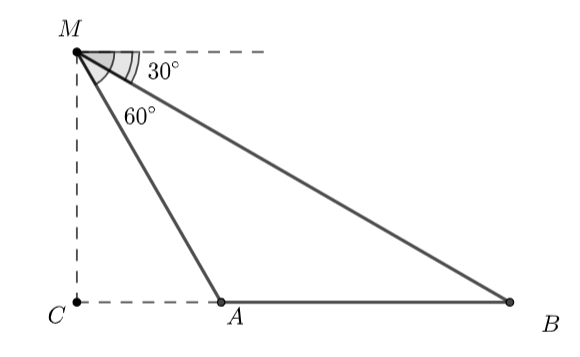
Giải bài 3.37 trang 43 sách bài tập toán 10 - Kết nối tri thức với cuộc sốngMột người đứng trên đài quan sát đặt ở cuối một đường đua thẳng. Ở độ cao 6m so với mặt đường đua, tại một thời điểm người đó nhìn hai vận động viên A và B dưới các góc tương ứng Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Một người đứng trên đài quan sát đặt ở cuối một đường đua thẳng. Ở độ cao 6m so với mặt đường đua, tại một thời điểm người đó nhìn hai vận động viên A và B dưới các góc tương ứng là \({60^ \circ }\) và \({30^ \circ },\) so với phương nằm ngang (H.3.6). Khoảng cách giữa hai vận động viên A và B (làm tròn đến hàng đơn vị, theo đơn vị mét) tại thời điểm đó là:
A. \(8m.\) B. \(7m.\) C. \(6m.\) D. \(9m.\) Phương pháp giải - Xem chi tiết - Tính \(\widehat {AMB}\), \(\widehat {CMA}\) và \(\widehat {MBA}\) - Tính \(MA\): \(MA = \frac{{MC}}{{\cos \widehat {CMA}}}.\) - Chứng minh \(\Delta MAB\) cân tại \(A\) thì \(MA = AB\) Lời giải chi tiết Ta có: \(\widehat {AMB} = {60^ \circ } - {30^ \circ } = {30^ \circ }.\) Ta có: \(\widehat {CMA} = {90^ \circ } - {60^ \circ } = {30^ \circ }.\) Ta có: \(\widehat {CMB} = {30^ \circ } + {30^ \circ } = {60^ \circ }.\) Xét \(\Delta CMB\) vuông tại \(C\) có: \(\widehat B = {90^ \circ } - \widehat {CMB} = {90^ \circ } - {60^ \circ } = {30^ \circ }\) Xét \(\Delta CMA\) vuông tại \(C\) có: \(MA = \frac{{MC}}{{\cos \widehat {CMA}}} = \frac{6}{{\cos {{30}^ \circ }}} = 4\sqrt 3 \,\,m.\) Xét \(\Delta ABM\) có \(\widehat {AMB} = \widehat B = {30^ \circ }\) \( \Rightarrow \,\,\Delta ABM\) cân tại \(A\) \( \Rightarrow \,\,AN = AB = 4\sqrt 3 \approx 7\,\,m\) Chọn B.
|