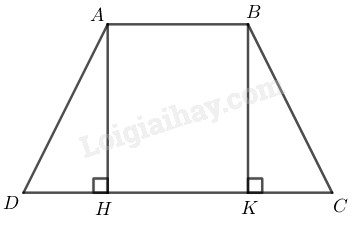
Bài 32 trang 83 SBT toán 8 tập 1

Đề bài

\(a)\) Hình thang cân \(ABCD\) có đáy nhỏ \(AB = b,\) đáy lớn \(CD = a,\) đường cao \(AH.\)Chứng minh rằng \(HD=\dfrac{a-b}{2},\) \(HC=\dfrac{a+b}{2},\) (\(a\) và \(b\) có cùng đơn vị đo)

\(b)\) Tính đường cao của hình thang cân có hai đáy \(10cm,\) \(26cm\) và cạnh bên \(17cm.\)

Lời giải chi tiết

\(a)\) Kẻ đường cao \(BK\)

Xét hai tam giác vuông \(AHD\) và \(BKC,\) ta có:

\(\widehat {AHB} = \widehat {BKC} = {90^0}\) 

\(AD = BC\) (tính chất hình thang cân)

\(\widehat D = \widehat C\)  (do ABCD là hình thang cân có đáy AB, CD)

Do đó: \(∆ AHD = ∆ BKC\) (cạnh huyền- góc nhọn)

\(⇒ HD = KC\)

Vì ABCD là hình thang có hai đáy AB, CD nên \(AB//CD\) hay \(AB//HK\). Suy ra \(ABHK\) là hình thang. 

Ta có: \(AH//BK\) (cùng vuông góc với \(CD\))

Hình thang \(ABKH\) có hai cạnh bên \(AH,\;BK\) song song nên \(AB = HK\)

\(a−b = DC – AB = DC – HK\)\( = HD + KC = 2HD\)

\( \Rightarrow HD =\displaystyle {{a - b} \over 2}\)

\(HC = DC-HD = a - \displaystyle{{a - b} \over 2}\)\( = \displaystyle{{a + b} \over 2}\)

\( b)\) \(HD = \displaystyle{{CD - AB} \over 2}\)\( = \displaystyle{{26 - 10} \over 2} = 8\left( {cm} \right)\)

Trong tam giác vuông \(AHD\) có \(\widehat {AHD} = {90^0}\)

\(A{D^2} = A{H^2} + H{D^2}\) (định lí Py-ta-go)

\(\eqalign{
& \Rightarrow A{H^2} = A{D^2} - H{D^2} \cr 
& \Rightarrow A{H^2} = {17^2} - {8^2} = 289 - 64 = 225 \cr 
& \Rightarrow AH = 15(cm) \cr} \)

HocTot.Nam.Name.Vn