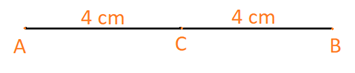
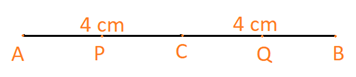
Giải bài 30 trang 95 sách bài tập Toán 6 – Cánh Diều Tập 2a) Vẽ đoạn thẳng AB có độ dài 8 cm và trung điểm C của đoạn thẳng đó. b) Vẽ các điểm P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB c) Tính độ dài các đoạn thẳng AP, QB và PQ. Tổng hợp đề thi học kì 2 lớp 6 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài a) Vẽ đoạn thẳng AB có độ dài 8 cm và trung điểm C của đoạn thẳng đó. b) Vẽ các điểm P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB c) Tính độ dài các đoạn thẳng AP, QB và PQ. Phương pháp giải - Xem chi tiết Trung điểm O của đoạn thẳng AB là điểm nằm giữa A và B sao cho OA=OB Nếu O là trung điểm của đoạn thẳng AB thì OA=OB=AB2 Lời giải chi tiết a) Đoạn thẳng AB có độ dài 8 cm và C là trung điểm của đoạn thẳng đó. Vì C là trung điểm AB nên CA=CB=AB2=82=4cm b) P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB c) Ta có: P là trung điểm AC nên PA=PC=AC2=42=2cm Q là trung điểm BC nên QB=QC=BC2=42=2cm Mà: PQ=PC+CQ(vì C nằm giữa P và Q) ⇒PQ=2+2=4(cm) Vậy AP=2cm;QB=2cm;PQ=4cm
|