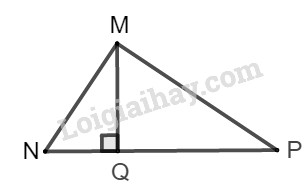
Bài 30 trang 107 SBT toán 9 tập 1Giải bài 30 trang 107 sách bài tập toán 9. Đường cao MQ của tam giác vuông MNP chia cạnh huyền NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotgN và cotgP. Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần? Đề bài Đường cao \(MQ\) của tam giác vuông MNP chia cạnh huyền \(NP\) thành hai đoạn \(NQ = 3, PQ = 6\). Hãy so sánh \(cotgN\) và \(cotgP\). Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần? Phương pháp giải - Xem chi tiết Các tỉ số lượng giác của góc nhọn (hình vẽ) được định nghĩa như sau:
\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\) Lời giải chi tiết
Tam giác \(MNQ\) vuông tại \(Q\) nên ta có: \(\cot g\widehat N = \dfrac{{NQ}}{{MQ}} = \dfrac{3}{{MQ}}\) Tam giác \(MPQ\) vuông tại \(Q\) nên ta có: \(\cot g\widehat P = \dfrac{{PQ}}{{MQ}} = \dfrac{6}{{MQ}}\) Ta có: \( \dfrac{6}{{MQ}} > \dfrac{3}{{MQ}}\) nên \(\cot g\widehat P > \cot g\widehat N\) \( \dfrac{{\cot g\widehat P}}{{\cot g\widehat N}} = \dfrac{{\dfrac{6}{{MQ}}}}{{\dfrac{3}{{MQ}}}}\) = \(\dfrac{6}{ {MQ}}.\dfrac{{MQ}}{3}\) = \(\dfrac{6}{3} = 2\) Vậy \(\cot g\widehat P = 2\cot g\widehat N.\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
