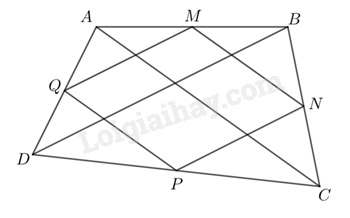
Giải bài 3 trang 65 SGK Toán 8 – Cánh diều

Đề bài

Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA.

a)      Chứng minh tứ giác MNPQ là hình bình hành.

b)     Cho \(AC = BD\). Chứng minh tứ giác MNPQ là hình thoi.

c)      Cho \(AC \bot BD\). Chứng minh tứ giác MNPQ là hình chữ nhật.

Lời giải chi tiết

a)      Vì M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác ABC.

\( \Rightarrow \left\{ \begin{array}{l}MN//AC\\MN = \frac{1}{2}AC\end{array} \right.\)

Vì P và Q lần lượt là trung điểm của CD và DA nên PQ là đường trung bình của tam giác ACD.

\( \Rightarrow \left\{ \begin{array}{l}PQ//AC\\PQ = \frac{1}{2}AC\end{array} \right.\)

Khi đó \(MN//PQ\) và \(MN = PQ\).

Vậy tứ giác MNPQ là hình bình hành (dhnb).

b)     Vì Q và M lần lượt là trung điểm của DA và AB nên QM là đường trung bình của tam giác ABD.

\( \Rightarrow QM = \frac{1}{2}BD\)

Mà \(AC = BD\) và \(MN = \frac{1}{2}AC\) nên \(QM = MN\).

Mà MNPQ là hình bình hành nên khi đó MNPQ là hình thoi (dhnb).

c)      Ta có:

\(\left. \begin{array}{l}AC \bot BD\\QM//BD\\MN//AC\end{array} \right\} \Rightarrow QM \bot MN\)

Mà MNPQ là hình bình hành nên khi đó MNPQ là hình chữ nhật (dhnb).