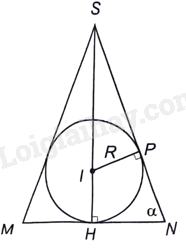
Giải bài 27 trang 52 sách bài tập toán 12 - Kết nối tri thứcMột hình chóp tứ giác đều ngoại tiếp hình cầu bán kính R. a) Chứng minh thể tích khối chóp tương ứng là (V = frac{{4{R^2}{x^2}}}{{3left( {x - 2R} right)}}), trong đó x là chiều cao hình chóp. b) Với giá trị nào của x để khối chóp tương ứng có thể tích nhỏ nhất? Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Một hình chóp tứ giác đều ngoại tiếp hình cầu bán kính R. a) Chứng minh thể tích khối chóp tương ứng là \(V = \frac{{4{R^2}{x^2}}}{{3\left( {x - 2R} \right)}}\), trong đó x là chiều cao hình chóp. b) Với giá trị nào của x để khối chóp tương ứng có thể tích nhỏ nhất? Phương pháp giải - Xem chi tiết Ý a: Mặt phẳng đi qua đường cao SH của hình chóp và trung điểm M của một cạnh đáy cắt hình chóp cắt hình chóp theo tam giác cân SMN và cắt hình cầu theo hình tròn tâm I bán kính R nội tiếp tam giác SMN. Có thể tính thể tích khối chóp theo x và \(\alpha = \widehat {SNH}\). Sauđó sử dụng đẳng thức \(x = R + IS\) để tìm hệ thức giữa R, x, \(\alpha \). Ý b: Tìm giá trị nhỏ nhất của \(V = \frac{{4{R^2}{x^2}}}{{3\left( {x - 2R} \right)}}\).
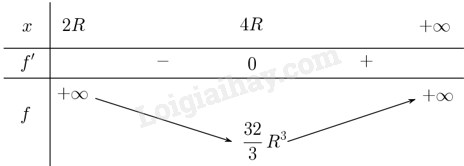
Lời giải chi tiết a) Ta có \(HN = x\cot \alpha ;MN = 2x\cot \alpha \). Thể tích khối chóp là \(V = \frac{1}{3}M{N^2} \cdot SH = \frac{4}{3}{x^3}{\cot ^2}\alpha \). Ta tính \({\cot ^2}\alpha \) theo R và x. Từ đẳng thức \(SH = IH + IS\) ta có \(x = R + \frac{R}{{\cos \alpha }}\). Do đó \(\cos \alpha = \frac{R}{{x - R}}\) suy ra \({\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - \frac{{{R^2}}}{{{{\left( {x - R} \right)}^2}}} = \frac{{{x^2} - 2Rx}}{{{{\left( {x - R} \right)}^2}}};{\cot ^2}\alpha = \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{R^2}}}{{x\left( {x - 2R} \right)}}\) Từ đó ta được \(V = \frac{{4{R^2}{x^2}}}{{3\left( {x - 2R} \right)}}\). b) Xét hàm số \(f\left( x \right) = \frac{{4{R^2}{x^2}}}{{3\left( {x - 2R} \right)}},x > 2R\). Ta có bảng biến thiên
Dựa vào bảng biến thiên ta có \(\min V = \frac{{32}}{3}{R^3}\) khi \(x = 4R\).
|