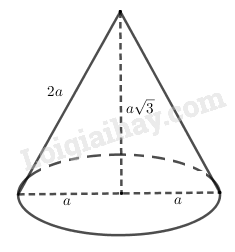
Bài 2.44 trang 66 SBT hình học 12Giải bài 2.44 trang 66 sách bài tập hình học 12. Cho một hình nón với thiết diện qua trục là một tam giác đều cạnh 2a... Đề bài Cho một hình nón với thiết diện qua trục là một tam giác đều cạnh \(2a\) có diện tích xung quanh là \({S_1}\) và một mặt cầu có đường kính bằng chiều cao hình nón có diện tích \({S_2}\). Khi đó hệ thức giữa \({S_1}\) và \({S_2}\) là: A. \({S_1} = {S_2}\) B. \({S_1} = 4{S_2}\) C. \({S_2} = 2{S_1}\) D. \(2{S_2} = 3{S_1}\) Phương pháp giải - Xem chi tiết Dựng hình, tính các diện tích xung quanh của hình nón và diện tích mặt cầu rồi so sánh. Chú ý: \({S_{xq}} = \pi rl\), \({S_{mc}} = 4\pi {r^2}\). Lời giải chi tiết
Bán kính đáy hình nón là \(a\), chiều cao là \(a\sqrt 3 \), đường sinh là \(2a\). Diện tích xung quanh \({S_1} = \pi rl = \pi .a.2a = 2\pi {a^2}\). Mặt cầu có bán kính \(\dfrac{{a\sqrt 3 }}{2}\) nên \({S_2} = 4\pi .{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)^2} = 3\pi {a^2}\). Do đó \(\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{2\pi {a^2}}}{{3\pi {a^2}}} \Rightarrow 3{S_1} = 2{S_2}\). Chọn D. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
|
