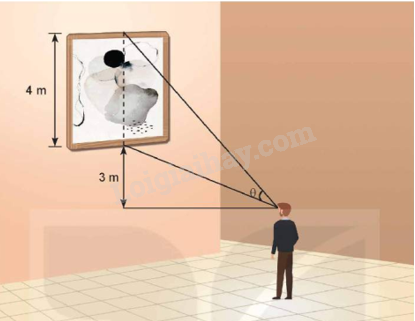
Giải bài 2.15 trang 45 Chuyên đề học tập Toán 12 - Kết nối tri thứcMột bức tranh cao 4 m được treo trên tường có mép dưới cao hơn tầm mắt người quan sát là 3 m (như hình vẽ). Người quan sát phải đứng cách tường bao nhiêu mét để có được tầm nhìn thuận lợi (tức là, có góc nhìn θ lớn nhất)? Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Hoá - Sinh - Sử - Địa Đề bài Một bức tranh cao 4 m được treo trên tường có mép dưới cao hơn tầm mắt người quan sát là 3 m (như hình vẽ). Người quan sát phải đứng cách tường bao nhiêu mét để có được tầm nhìn thuận lợi (tức là, có góc nhìn θ lớn nhất)?
Phương pháp giải - Xem chi tiết Sử dụng đạo hàm để giải quyết bài toán tối ưu. Lời giải chi tiết
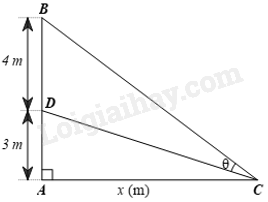
Đặt AC = x (m) ta có CD=√x2+9, BC=√x2+49 Ta có: sinB=x√x2+49 Xét tam giác BDC có: CDsinB=BDsinθ⇔√x2+9x√x2+49=4sinθ⇔sinθ=4x√x2+49.√x2+9 Để có được tầm nhìn thuận lợi thì góc nhìn θ lớn nhất. Xét hàm số y=4x√x2+49.√x2+9=4x√x4+58x2+441,x>0 Ta có: y′=−4x4+1764(x4+58x2+441)√x4+58x2+441=0⇔x=√21≈4,58 Vậy người đó phải đứng cách tường khoảng 4,58m thì tầm nhìn là thuận lợi nhất.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM; 70+ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|