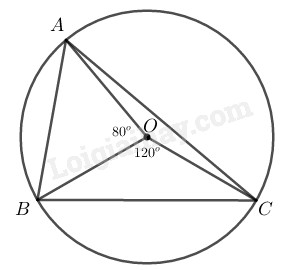
Bài 2.1 phần bài tập bổ sung trang 101 SBT toán 9 tập 2Giải bài 2.1 phần bài tập bổ sung trang 101 sách bài tập toán 9. Cho đường tròn tâm O bán kính R... Đề bài Cho đường tròn tâm \(O\) bán kính \(R.\) Vẽ góc ở tâm \(\widehat {AOB} = {80^0}\), vẽ góc ở tâm \(\widehat {BOC} = {120^0}\) kề với \(\widehat {AOB}\). So sánh và sắp xếp độ dài \(AB, BC, CA\) theo thứ tự tăng dần. Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. +) Với hai cung trong một đường tròn, cung lớn hơn căng dây lớn hơn. Lời giải chi tiết
Ta có: \(\widehat {AOB} = {80^o}\); \(\widehat {BOC} = {120^o}\) Suy ra: \(\widehat {AOC} = 360^o-80^o-120^o={160^o}\) \(sđ \overparen{AB} = \widehat {AOB}={80^o}\) \( sđ \overparen{BC}= \widehat {BOC}={120^o}\) \( sđ \overparen{AC}= \widehat {AOC}={160^o}\) \(\widehat {AOB} < \widehat {BOC} < \widehat {AOC}\) Suy ra \(\overparen{AB} < \overparen{BC} < \overparen{AC}\) Suy ra: \(AB < BC < AC\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
