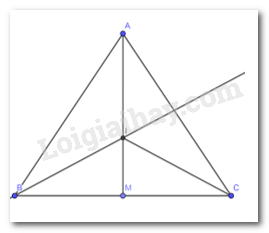
Giải bài 2 trang 82 SGK Toán 7 tập 2 - Chân trời sáng tạoCho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C. Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC cân tại A. Kẻ đường trung tuyến AM. Tia phân giác của góc B cắt AM tại I. Chứng minh rằng CI là tia phân giác của góc C. Phương pháp giải - Xem chi tiết - Ta chứng minh I là giao của 3 đường phân giác trong tam giác ABC - Từ đó ta chứng minh CI là phân giác góc C Lời giải chi tiết
Xét tam giác ABM và tam giác ACM có : AM chung BM = CM ( M là trung điểm BC ) AB = AC (tam giác ABC cân tại A theo giả thiết) \( \Rightarrow \Delta AMB = \Delta AMC (c-c-c)\) \( \Rightarrow \widehat{BAM}= \widehat{CAM}\) (2 góc tương ứng) \( \Rightarrow \) AM thuộc tia phân giác của góc A Mà AM cắt tia phân giác góc B tại I \( \Rightarrow \) I là giao của các đường phân giác trong tam giác ABC \( \Rightarrow \) CI là phân giác góc C (định lí 3 đường phân giác cắt nhau tại 1 điểm)  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
