Giải bài 2 trang 46, 47, 48 Chuyên đề học tập Toán 11 Chân trời sáng tạoĐồ thị ở Hình 6 biểu diễn năm ngôi làng A, B, C, D và E cùng các con đường giữa chúng (mỗi cạnh biểu diễn một con đường giữa hai ngôi làng) Tổng hợp đề thi học kì 2 lớp 11 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh
Lựa chọn câu để xem lời giải nhanh hơn
Khám phá 2 Đồ thị ở Hình 6 biểu diễn năm ngôi làng A, B, C, D và E cùng các con đường giữa chúng (mỗi cạnh biểu diễn một con đường giữa hai ngôi làng). Biết rằng mỗi con đường ra, vào làng đều phải đi qua một cổng chào; hai con đường khác nhau thì ra, vào làng qua hai cổng chào khác nhau. Ngoài ra, các ngôi làng không còn cổng chào nào khác.
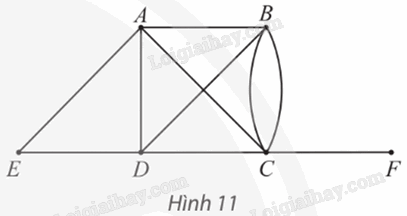
a) Ngôi làng nào có ít cổng chào nhất? Ngôi làng nào có nhiều cổng chào nhất? b) Năm ngôi làng có tất cả bao nhiêu cổng chào? Phương pháp giải: Quan sát hình 6 để trả lời Lời giải chi tiết: a) Do ta có 3 con đường để ra, vào ngôi làng A nên ngôi làng A có 3 cổng chào. Tương tự như vậy, ta có: ⦁ Ngôi làng B có 5 cổng chào; ⦁ Ngôi làng C có 2 cổng chào; ⦁ Ngôi làng D có 3 cổng chào; ⦁ Ngôi làng E có 3 cổng chào. Vậy ngôi làng có ít cổng chào nhất là ngôi làng C (với 2 cổng chào); ngôi làng có nhiều cổng chào nhất là ngôi làng B (với 5 cổng chào). b) Quan sát Hình 6, đồ thị có tất cả 8 cạnh (mỗi cạnh biểu diễn 1 con đường giữa hai ngôi làng) nên năm ngôi làng có tất cả 8 cổng chào. Thực hành 2 Cho đồ thị như Hình 11.
a) Hãy chỉ ra bậc của tất cả các đỉnh và tìm tổng của chúng. b) Tìm tất cả các đỉnh kề với đỉnh B. Số đỉnh này có bằng bậc của đỉnh B không? Phương pháp giải: Bậc của một đỉnh A trong đồ thị G là số cạnh của đồ thị nhận đỉnh A làm đầu mút, kí hiệu là d(A) Lời giải chi tiết: a) Số cạnh của đồ thị có A là đầu mút là: 4.Suy ra bậc của đỉnh A là: d(A) = 4. Tương tự như vậy, ta có: d(B) = 4; d(C) = 5; d(D) = 4; d(E) = 2; d(F) = 1. Tổng các bậc của các đỉnh của đồ thị là: 4 + 4 + 5 + 4 + 2 + 1 = 20. b) Tất cả các đỉnh kề với đỉnh B là: A, C, D.Suy ra có 3 đỉnh kề với đỉnh B. Mà bậc của đỉnh B là: d(B) = 4. Vì 3 ≠ 4 nên 3 ≠ d(B). Vậy số đỉnh kề với đỉnh B không bằng bậc của đỉnh B. Vận dụng 2 Có hay không một đồ thị có ba đỉnh, trong đó hai đỉnh có bậc bằng 2 và một đỉnh có bậc bằng 3? Phương pháp giải: Trong một đồ thị, tổng tất cả bậc của đỉnh là một số chẵn và bằng hai lần số cạnh của đồ thị Lời giải chi tiết: Không có, vì tổng tất cả các bậc của các đỉnh là 2 + 2 + 3 = 7 là một số lẻ.
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|