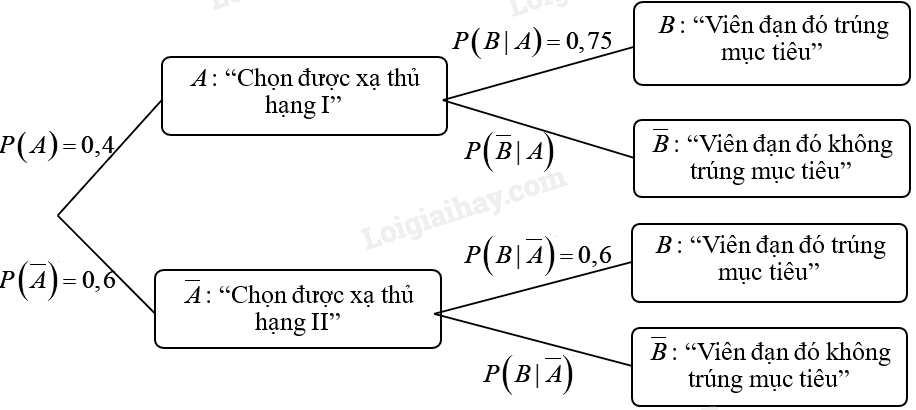
Giải bài 16 trang 95 sách bài tập toán 12 - Cánh diềuMột đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6. Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu. Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Một đội tuyển thi bắn súng có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xác suất bắn trúng mục tiêu của xạ thủ hạng I và hạng II lần lượt là 0,75 và 0,6. Chọn ngẫu nhiên một xạ thủ và xạ thủ đó chỉ bắn 1 viên đạn. Sử dụng sơ đồ hình cây, tính xác suất để viên đạn đó trúng mục tiêu. Phương pháp giải - Xem chi tiết ‒ Sử dụng sơ đồ hình cây. ‒ Sử dụng công thức tính xác suất toàn phần: \(P\left( A \right) = P\left( B \right).P\left( {A|B} \right) + P\left( {\overline B } \right).P\left( {A|\overline B } \right)\). Lời giải chi tiết Xét các biến cố: \(A\): “Chọn được xạ thủ hạng I”; \(B\): “Viên đạn đó trúng mục tiêu”; Có 10 xạ thủ, bao gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II nên ta có \(P\left( A \right) = \frac{4}{{10}} = 0,4;P\left( {\overline A } \right) = \frac{6}{{10}} = 0,6\) Xác suất bắn trúng mục tiêu của xạ thủ hạng I và 0,75 nên ta có \(P\left( {B|A} \right) = 0,75\). Xác suất bắn trúng mục tiêu của xạ thủ hạng II và 0,6 nên ta có \(P\left( {B|\overline A } \right) = 0,6\). Ta có sơ đồ hình cây như sau: Vậy xác suất của biến cố \(B\): “Viên đạn đó trúng mục tiêu” là: \(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right) = 0,4.0,75 + 0,6.0,6 = 0,66\).  Chia sẻ Bình luận
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
