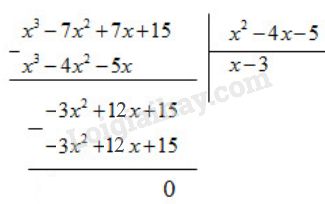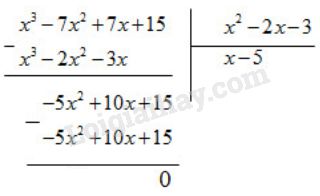Bài 16 trang 28 SBT toán 8 tập 1Giải bài 16 trang 28 sách bài tập toán 8. Hãy quy đồng mẫu thức. Cho hai phân thức ... Đề bài Cho hai phân thức \(\displaystyle {1 \over {{x^2} - 4x - 5}}\) và \(\displaystyle {2 \over {{x^2} - 2x - 3}}\) Chứng tỏ rằng có thể chọn đa thức \({x^3} - 7{x^2} + 7x + 15\) làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. Hãy quy đồng mẫu thức. Phương pháp giải - Xem chi tiết Thực hiện phép chia đa thức \({x^3} - 7{x^2} + 7x + 15\) cho hai đa thức \({{x^2} - 4x - 5}\) và \({{x^2} - 2x - 3}\). Nếu các phép chia đều là phép chia hết thì đa thức \({x^3} - 7{x^2} + 7x + 15\) là mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. Lời giải chi tiết Ta có:
Suy ra: \({x^3} - 7{x^2} + 7x + 15 \)\(\,= \left( {{x^2} - 4x - 5} \right)\left( {x - 3} \right)\)
Suy ra: \({x^3} - 7{x^2} + 7x + 15 \)\(\,= \left( {{x^2} - 2x - 3} \right)\left( {x - 5} \right)\) Vậy đa thức \({x^3} - 7{x^2} + 7x + 15\) là mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. * Quy đồng: \(\displaystyle {1 \over {{x^2} - 4x - 5}}\) \(\displaystyle= {{1.\left( {x - 3} \right)} \over {\left( {{x^2} - 4x - 5} \right).\left( {x - 3} \right)}}\) \(\displaystyle= {{x - 3} \over {{x^3} - 7{x^2} + 7x + 15}}\) \(\displaystyle{2 \over {{x^2} - 2x - 3}} \) \(\displaystyle= {{2.\left( {x - 5} \right)} \over {\left( {{x^2} - 2x - 3} \right)\left( {x - 5} \right)}} \) \(\displaystyle= {{2\left( {x - 5} \right)} \over {{x^3} - 7{x^2} + 7x + 15}} \) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
