Bài 1.5, 1.6, 1.7 trang 3, 4 SBT Vật Lí 12Giải bài 1.5, 1.6, 1.7 trang 3, 4 sách bài tập vật lí 12.Phương trình dao động điều hoà của một chất điểm
Lựa chọn câu để xem lời giải nhanh hơn
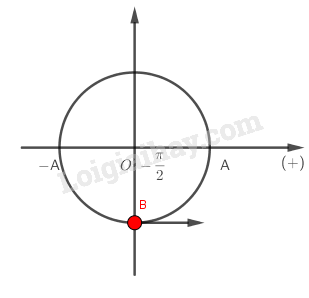
1.5 Phương trình dao động điều hoà của một chất điểm là \(x = A\cos \left( {\omega t - {\pi \over 2}} \right)\,cm\). Hỏi gốc thời gian được chọn vào lúc nào ? A. Lúc chất điểm qua vị trí cân bằng theo chiều dương. B. Lúc chất điểm qua vị trí cân bằng theo chiều âm. C. Lúc chất điểm ở vị trí biên x = \(+A\). D. Lúc chất điểm ở vị trí biên x= \(-A\). Phương pháp giải: Thay \(t = 0\) vào phương trình giao động điều hòa, dùng vòng tròn lượng giác xét chiều chuyển động của vật Lời giải chi tiết: Thay \(t = 0\) vào phương trình \(x = A\cos (\omega t - \dfrac{\pi }{2})\) ta được \({x_0} = A\cos (\omega .0 - \dfrac{\pi }{2}) = 0\) Pha dao động tại \(t = 0\) là \(\varphi = - \dfrac{\pi }{2}\) , ta có:
Vậy gốc thời gian là lúc vật qua vị trí cân bằng theo chiều dương. Chú ý: Ta có dấu của vận tốc \(v\) và \(\sin (\omega t + \varphi )\) trái nhau, do vậy dựa vào dấu pha dao động ta có thể xác định chiều chuyển động của vật. Ta có: \(\sin ( - \dfrac{\pi }{2}) = - 1 < 0 \Rightarrow v > 0\) Chọn A 1.6 Một vật nhỏ dao động điều hoà theo phương trình \(x = 10\cos \left( {\pi t + {\pi \over 6}} \right)\,(cm)\) Lấy \({\pi ^2} = 10\) Gia tốc của vật có độ lớn cực đại là A.\(10\pi cm/{s^2}\). B.\(10cm/{s^2}\). C.\(100cm/{s^2}\). D.\(100\pi cm/{s^2}\). Phương pháp giải: Vận dụng công thức tính độ lớn gia tốc cực đại: \({a_{\max }} = A.{\omega ^2}\) Lời giải chi tiết: Từ phương trình \(x = 10\cos \left( {\pi t + {\pi \over 6}} \right)\,(cm)\), ta có \(A = 10(cm)\), \(\omega = \pi (rad/s)\) Gia tốc có độ lớn cực đại là: \({a_{\max }} = A.{\omega ^2} = 10{\pi ^2} = 10.10 = 100(cm/{s^2})\) Chọn C 1.7 Một chất điểm dao động điều hoà theo phương trình :\(x = 2\cos \left( {2 \pi t + {\pi \over 2}} \right)\,cm\). Tại \(t = 0,25 s\) chất điểm có li độ bằng A. \( \sqrt{3} \) cm. B. \( -\sqrt{3} \) cm. C. \(2 cm\). D. \(-2 cm\). Phương pháp giải: Thay thời điểm t vào phương trình dao động điều hòa. Lời giải chi tiết: Thay \(t = \dfrac{1}{4}s\) vào phương trình \(x = 2\cos (2\pi t + \dfrac{\pi }{2})\) ta được: \(x = 2\cos (2\pi .\dfrac{1}{4} + \dfrac{\pi }{2}) = - 2(cm)\) Chọn D HocTot.Nam.Name.Vn
|