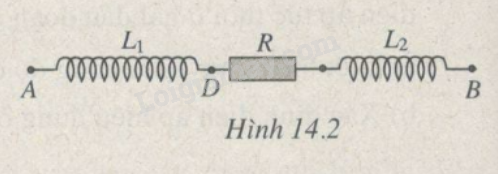
Bài 14.15 trang 41 SBT Vật Lí 12

Đề bài

Cho mạch điện gồm ba phần tử mắc nối tiếp $(H.14.2)$ ${L_1} = \dfrac{{0,1}}{\pi }(H);$ $R = 40\Omega ;$ ${L_2} = \dfrac{{0,3}}{\pi }(H).$ Điện áp tức thời ở hai đầu đoạn mạch $u = 160\sqrt 2 {\rm{cos100}}\pi {\rm{t(V)}}{\rm{.}}$

a) Viết biểu thức của $i.$

b) Xác định ${U_{DB}}.$

Lời giải chi tiết

Cảm kháng ${Z_{{L_1}}} = {L_1}\omega  = \dfrac{{0,1}}{\pi }.100\pi  = 10\Omega$

${Z_{{L_2}}} = {L_2}\omega  = \dfrac{{0,3}}{\pi }.100\pi  = 30\Omega$

+ Tổng trở $Z = \sqrt {{R^2} + {{({Z_{{L_1}}} + {Z_{{L_2}}})}^2}} \\ = \sqrt {{{40}^2} + {{(10 + 30)}^2}}  = 40\sqrt 2 \Omega$

+ Cường độ dòng điện hiệu dụng: $I = \dfrac{U}{Z} = \dfrac{{160}}{{40\sqrt 2 }} = 2\sqrt 2 A \Rightarrow {I_0} = 4A$

Độ lệch pha giữa điện áp và dòng điện:

$\tan \varphi  = \dfrac{{{Z_{{L_1}}} + {Z_{{L_2}}}}}{R} = \dfrac{{30 + 10}}{{40}} = 1 \\\Rightarrow \varphi  = \dfrac{\pi }{4}rad$

Ta có $\varphi  = {\varphi _u} - {\varphi _i} \Rightarrow {\varphi _i} = {\varphi _u} - \varphi  =  - \dfrac{\pi }{4}(rad)$

Vậy biểu thức dòng điện là: $i = 4{\rm{cos(100}}\pi {\rm{t - }}\dfrac{\pi }{4}{\rm{)(A)}}$

 b) Ta có ${U_{DB}} = I.{Z_{R{L_2}}} = I.\sqrt {{R^2} + Z_{{L_2}}^2} \\ = 2\sqrt 2 .\sqrt {{{40}^2} + {{30}^2}}  = 100\sqrt 2 V$

HocTot.Nam.Name.Vn