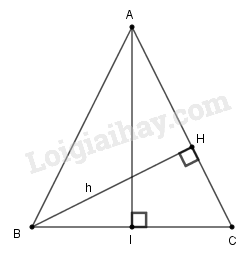
Bài 1.3 phần bài tập bổ sung trang 123 SBT toán 9 tập 1

Đề bài

Cho tam giác \(ABC\) cân tại \(A\), đường cao \(BH\). Hãy tính góc \(A\) và các cạnh \(AB, BC\), nếu biết \(BH = h\) và \(\widehat C = \alpha .\)

Lời giải chi tiết

Vì tam giác ABC cân tại A nên \(\widehat B = \widehat C = \alpha \)

Ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) (định lý tổng ba góc trong tam giác)

\( \Rightarrow \widehat A = {180^0} - \left( {\widehat B + \widehat C} \right)\) \( \Rightarrow \widehat A = 180^\circ  - 2\alpha .\)

Tam giác vuông \(HBC\) có \(BC = \dfrac{{BH}}{{\sin \widehat C}}= \displaystyle {h \over {\sin \alpha }}\).

Kẻ đường cao \(AI\) của tam giác cân \(ABC\) thì AI cũng là đường trung tuyến nên \(BI = IC = \dfrac{{BC}}{2}\)

Xét tam giác ACI vuông tại I, có: \(AC = \displaystyle {{IC} \over {\cos \alpha }} = { \displaystyle  {{{BC} \over 2}} \over {{\rm{cos}}\alpha }}\)\( = \displaystyle {h \over {2\sin \alpha \cos \alpha }}.\)

Vậy \(AB = AC =\) \(\displaystyle {h \over {2\sin \alpha \cos \alpha }}.\)

HocTot.Nam.Name.Vn