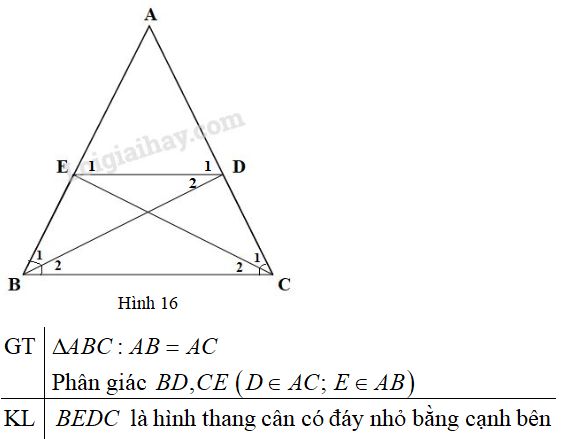
Bài 10 trang 99 Vở bài tập toán 8 tập 1Giải bài 10 trang 99 VBT toán 8 tập 1. Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên. GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn Đề bài Cho tam giác ABC cân tại A, các đường phân giác BD,CE (D∈AC,E∈AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên. Phương pháp giải - Xem chi tiết Sử dụng: - Hai tam giác bằng nhau có các cạnh tương ứng bằng nhau. - Tam giác cân có hai cạnh bên bằng nhau hai góc đáy bằng nhau. - Hai đường thẳng song song khi có cặp góc đồng vị bằng nhau. - Hình thang là tứ giác có hai cạnh đối song song. - Hình thang cân là hình thang có hai góc kề với một đáy bằng nhau. Lời giải chi tiết
∆ABD và ∆ACE có: AB = AC (vì tam giác ABC cân tại A) \widehat{A} chung \widehat {{B_1}} = \widehat {{C_1}} (vì \widehat {{B_1}} = \dfrac{1}{2}\widehat B,\,\widehat {{C_1}} = \dfrac{1}{2}\widehat C\,\,\text{và}\,\,\widehat B = \widehat C) Do đó \Delta ABD = \Delta ACE{\rm{ }}\left( {g.c.g} \right) suy ra A{\rm{D}} = A{\rm{E}} Tam giác ABC cân nên \widehat B = \widehat C = \left( {{{180}^o} - \widehat A} \right):2 (1) Tam giác ADE cân nên \widehat {{E_1}} = \widehat {{D_1}} = \left( {{{180}^o} - \widehat A} \right):2 (2) Từ (1) và (2) suy ra \widehat B = \widehat {{E_1}}, hai góc này ở vị trí đồng vị nên ED//BC. Vậy BEDC là hình thang, lại có \widehat B = \widehat C nên là hình thang cân. Do ED//BC nên \widehat {{D_2}} = \widehat {{B_2}} (SLT), lại có \widehat {{B_1}} = \widehat {{B_2}} nên \widehat {{D_2}} = \widehat {{B_1}}, suy ra \Delta BDE cân, do đó EB = ED. HocTot.Nam.Name.Vn
|