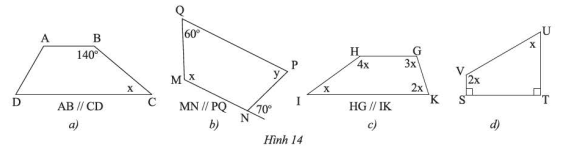
Giải bài 1 trang 71 SGK Toán 8 – Chân trời sáng tạo

Đề bài

Tìm $x$ và $y$ ở các hình sau.

Lời giải chi tiết

a) Vì $AB$ // $CD$ (gt) suy ra:

$\widehat B + \widehat C = 180^\circ$ (cặp góc trong cùng phía)

$\begin{array}{l}140^\circ  + x = 180^\circ \\x = 40^\circ \end{array}$

b) Vì $MN$ // $PQ$ (gt)

$\Rightarrow \widehat M + \widehat Q = 180^\circ$ (trong cùng phía)

$\begin{array}{l}x + 60^\circ  = 180^\circ \\x = 120^\circ \end{array}$

Vì $MN$ // $PQ$ (gt)

$\Rightarrow y = \widehat P = \widehat N = 70^\circ$ (so le trong)

c) Xét tứ giác $IHGK$ ta có:

$\begin{array}{l}\widehat H + \widehat G + \widehat I + \widehat K = 360^\circ \\4x + 3x + 2x + x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10 = 36^\circ \end{array}$

d) Xét tứ giác $UVST$ ta có:

$\widehat U + \widehat V + \widehat S + \widehat T = 360^\circ$

$\begin{array}{l}x + 2x + 90^\circ  + 90^\circ  = 360^\circ \\3x + 180^\circ  = 360^\circ \\3x = 180^\circ \\x = 60^\circ \end{array}$