Bài 1. Các đặc trưng của dòng điện xoay chiều - Chuyên đề học tập Lí 12 Chân trời sáng tạo

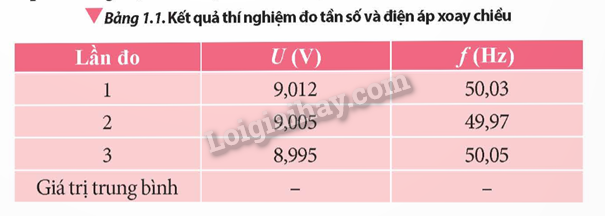
Câu hỏi tr 5 CHMĐ

Các thiết bị điện, điện tử mà chúng ta sử dụng trong sinh hoạt và sản xuất hiện nay như: bóng đèn, ti vi, máy giặt, tủ lạnh, điều hoà, quạt điện, động cơ điện,.. chủ yếu dùng dòng điện xoay chiều. Vậy, dòng điện xoay chiều là gì? Nó có những đại lượng đặc trưng gì và các đo các đại lượng đó như thế nào?

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

Dòng điện xoay chiều là dòng điện có cường độ biến thiên điều hoà theo thời gian.

Dòng điện xoay chiều có các đại lượng đặc trưng là:

- Giá trị hiệu dụng (U): dùng đồng hồ đo vạn năng ở thang đo dòng điện xoay chiều.

- Giá trị cực đại (I_max): Sử dụng máy hiện sóng để quan sát dạng sóng của dòng điện xoay chiều và xác định giá trị cực đại.

- Tần số (f): Sử dụng đồng hồ đo tần số hoặc máy hiện sóng.

- Chu kỳ (T): tính toán bằng công thức \(T = \frac{1}{f}\)

Câu hỏi tr 5 CH

Hãy viết biểu thức cường độ dòng điện và điện áp xoay chiều. Giải thích các đại lượng. So sánh giá trị hiệu dụng và giá trị cực đại của cường độ dòng điện, điện áp.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

- Biểu thức của cường độ dòng điện xoay chiều: 

\(i = {I_0}\cos (\omega t + {\varphi _i})\)

Với i là cường độ dòng điện tức thời (A).

I₀ là cường độ dòng điện cực đại (A).

ω là tần số góc của dòng điện (rad/s).

φ_i là pha ban đầu của cường độ dòng điện.

- Biểu thức của điện áp xoay chiều:

\(u = {U_0}\cos (\omega t + {\varphi _u})\) 

Với u là điện áp tức thời (V).

U₀ là điện áp cực đại (V).

φ_u là pha ban đầu của điện áp.

- Giá trị hiệu dụng nhỏ hơn giá trị cực đại của cường độ dòng điện vì \(I = \frac{{{I_0}}}{{\sqrt 2 }}\), trong đó I là cường độ dòng điện hiệu dụng và I₀ là cường độ cực đại của dòng điện.

- Giá trị hiệu dụng nhỏ hơn giá trị cực đại của điện áp vì \(U = \frac{{{U_0}}}{{\sqrt 2 }}\), trong đó U là điện áp hiệu dụng và U₀ là điện áp cực đại.

Câu hỏi tr 6 LT

Từ đồ thị cường độ của dòng điện xoay chiều theo thời gian ở Hình 1.2, hãy xác định:

a) Biên độ, tần số, chu kì, tần số góc, pha ban đầu, cường độ dòng điện hiệu dụng.

b) Biểu thức cường độ dòng điện tức thời.

c) Khoảng thời gian cường độ dòng điện tăng trong chu kì đầu tiên.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

a) Biên độ I₀ = 2 A, chu kì T = 0,02 s, tần số góc \(\omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,02}} = 100\pi (rad/s)\) rad/s

Pha ban đầu là 0, cường độ dòng điện hiệu dụng là: \(I = \frac{{{I_0}}}{{\sqrt 2 }} = \frac{2}{{\sqrt 2 }}\)

b) Biểu thức cường độ dòng điện tức thời là:

\(i = 2\cos (100\pi t)\)

c) Khoảng thời gian cường độ dòng điện tăng trong chu kì đầu tiên là:

\(t = \frac{T}{2} = \frac{{0,02}}{2} = 0,01s\)

Câu hỏi tr 7 CH

Từ các dụng cụ thí nghiệm như Hình 1,4, đề xuất phương án thí nghiệm đo tần số và điện áp của dòng điện xoay chiều từ đầu ra của biến áp nguồn.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

- Dụng cụ: biến áp nguồn có điện áp đầu ra xoay chiều và có thể thay đổi được; đồng hồ đo điện đa năng hiện số có chức năng đo tần số; que đo đồng hồ đa năng, dây dẫn điện, đồng hồ đo điện áp.

- Tiến hành:

+ Bước 1: Chuẩn bị dụng cụ thí nghiệm: kiểm tra kĩ các dụng cụ thí nghiệm xem có hoạt động bình thường không. Đọc kĩ hướng dẫn sử dụng của các dụng cụ thí nghiệm.

+ Bước 2: Kết nối mạch điện: Cắm hai dây nối của que đo vào đồng hồ điện đa năng, sau đó cắm hai đầu kim nhọn của hai dây nối vào hai lỗ cắm đầu ra của biến áp nguồn.

+ Bước 3: Bật nguồn điện xoay chiều sau đó đọc giá trị và ghi lại kết quả.

+ Bước 4: Lặp lại bước 3 hai lần.

+ Bước 5: Tắt biến áp nguồn và rút phích cắm khỏi ổ điện. Tắt đồng hồ đo.

Câu hỏi tr 8 TN

Báo cáo kết quả thí nghiệm (số liệu minh hoạ)

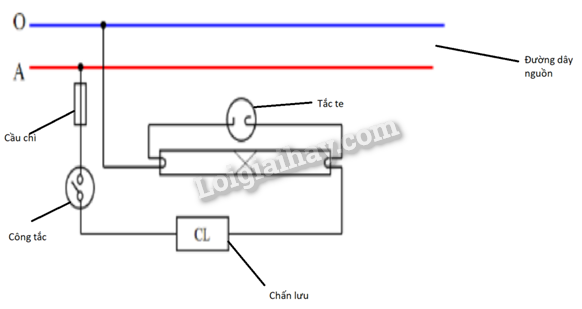
- Xác định độ chia nhỏ nhất của phép đo tần số, điện áp trên đồng hồ.

- Tính giá trị trung bình, sai số và viết kết quả. Nhận xét giá trị tần số đo được với tần số đã biết của mạng lưới điện.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

- Độ chia nhỏ nhất của phép đo tần số là 0,01 và độ chia nhỏ nhất của phép đo điện áp là 0,001.

- Giá trị trung bình của tần số là: \(\overline f  = \frac{{50,03 + 49,97 + 50,05}}{3} = 50,02\)

- Giá trị trung bình của điện áp là: \(\overline U  = \frac{{9,012 + 9,005 + 8,995}}{3} = 9,004\)

- Sai số của phép đo điện áp khoảng 0,1%.

- Sai số của phép đo tần số khoảng 1%.

- Nhận xét: Tần số đã biết của mạng lưới điện thường là 50 Hz.

+ Độ chênh lệch giữa giá trị đo được và tần số đã biết của mạng lưới điện là 0,02 Hz.

+ Độ chênh lệch này khác nhỏ, có thể do sai số của đồng hồ đo tần số, có thể do dụng cụ chưa chuẩn.

+ Do độ chênh lệch khá là nhỏ nên không ảnh hưởng đến hoạt động của thiết bị điện.

Câu hỏi tr 8 LT 1

Thay biến áp nguồn bằng máy phát âm tần, thực hiện lại phép đo biên độ và tần số của tín hiệu xoay chiều do máy phát âm tần tạo ra.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

- Dụng cụ: chuẩn bị máy phát âm tần, máy đo dao động, dây dẫn điện, que đo đồng hồ đa năng.

- Tiến hành:

+ Bước 1: Thay biến áp nguồn bằng máy phát âm tần, thực hiện lại phép đo biên độ và tần số của tín hiệu xoay chiều do máy phát âm tần tạo ra.

+ Bước 2: : Kết nối mạch điện: Cắm hai dây nối của que đo vào đồng hồ điện đa năng, sau đó cắm hai đầu kim nhọn của hai dây nối vào hai lỗ cắm đầu ra của máy phát âm tần.

+ Bước 3: Cài đặt máy phát âm tần. Cài đặt tần số mong muốn trên máy phát âm tần. Sau đó điều chỉnh biên độ tín hiệu bằng núm vặn trên máy phát âm tần.

+ Bước 4: Đo biên độ và đo tần số. 

+ Bước 5: Đọc giá trị biên độ (điện áp hiệu dụng) và giá trị tần số hiển thị trên màn hình máy đo.

+ Bước 6: Ghi lại kết quả 

+ Bước 7: Đo lại khoảng 2-3 lần để được kết quả chính xác.

Câu hỏi tr 8 LT 2

Đặt vào hai đầu điện trở R một điện áp u biến thiên điều hoà theo thời gian. Từ thời điểm t₁ đến thời điểm t₂ điện áp u giảm từ giá trị 12V đến 3V thì cường độ dòng điện qua mạch tương ứng giảm từ giá trị i₁ = 1,6 A đến i₂. Tìm i₂

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

Ta có : \(i = \frac{u}{R} \to i \sim u\) (tỉ lệ thuận)

\(\frac{{{i_1}}}{{{i_2}}} = \frac{{{u_1}}}{{{u_2}}} \to \frac{{1,6}}{{{i_2}}} = \frac{{12}}{3} \to {i_2} = 0,4A\)

Câu hỏi tr 9 CH

Dựa vào biểu thức dung kháng \({Z_C} = \frac{1}{{\omega C}}\) , giải thích tại sao tụ điện lại không cho dòng điện một chiều đi qua.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

Tụ điện lại không cho dòng điện một chiều đi qua vì dòng điện một chiều có tần số (f) bằng 0 mà theo như biểu thức dung khác thì Z_c phụ thuộc vào tần số, nên không tụ điện không cho dòng điện một chiều đi qua.

Câu hỏi tr 10 CH

Dựa vào biểu thức cảm kháng \({Z_L} = \omega L\), tìm mối quan hệ giữa u và i khi đặt điện áp không đổi vào hai đầu cuộn cảm thuần.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

Ta có: u sớm pha hơn i một góc \(\frac{\pi }{2}\) nên u và i vuông pha nhau.

Ta viết được biểu thức: \(u = {U_0}\cos (\omega t + {\varphi _u})\); \(i = {I_0}\cos (\omega t + {\varphi _u} - \frac{\pi }{2})\).

Từ đó mối liên hệ giữa u và I khi đặt điện áp không đổi vào hai đầu cuộn cảm thuần là:

\(\frac{{{i^2}}}{{I_0^2}} + \frac{{{u^2}}}{{U_0^2}} = 1\)

Câu hỏi tr 11 LT

Điện áp \(u = 5\sqrt 2 \cos 100\pi t(V)\) vào hai đầu đoạn mạch RLC nối tiếp gồm điện trở thuần \(30\Omega \), cuộn cảm thuần có độ tự cảm \(\frac{{0,8}}{\pi }H\), tụ điện có điện dung \(\frac{{250}}{\pi }\mu F\).

a) Tính tổng trở toàn mạch.

b) Tính cường độ dòng điện cực đại, cường độ dòng điện hiệu dụng qua đoạn mạch.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

a) Cảm kháng là: \({Z_L} = \omega L = 100\pi .\frac{{0,8}}{\pi } = 80\Omega \).

Dung kháng là: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{250}}{\pi }{{.10}^{ - 6}}}} = 40\Omega \).

Tổng trở toàn mạch là: \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}}  = \sqrt {{{30}^2} + {{(80 - 40)}^2}}  = 50\Omega \).

b) Cường độ dòng điện cực đại là: \({I_0} = \frac{{{U_0}}}{Z} = \frac{{5\sqrt 2 }}{{50}} = \frac{{\sqrt 2 }}{{10}}A\).

Biểu thức cường độ dòng điện là: \(i = \frac{{\sqrt 2 }}{{10}}\cos \left( {100\pi t - \frac{\pi }{2}} \right)A\)

Cường độ dòng điện hiệu dụng là: \(i = \frac{{{I_0}}}{{\sqrt 2 }} = \frac{{\frac{{\sqrt 2 }}{{10}}}}{{\sqrt 2 }} = 0,1A\)

Câu hỏi tr 11 VD

Hình 1.13 mô tả một đèn huỳnh quang chiếu sáng trong phòng sử dụng dòng điện xoay chiều. Từ quan sát thực tiễn và tìm hiểu trên sách, báo, internet,.. em hãy vẽ lại sơ đồ mạch điện đơn giản của đèn huỳnh quang và cho biết tác dụng của cuộn chấn lưu và tắc te.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

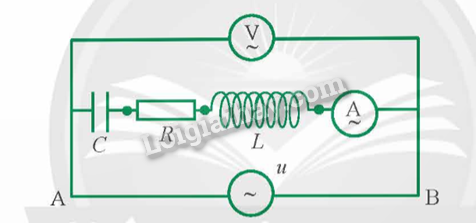
- Tác dụng của cuộn chấn lưu: 

+ Giúp ổn định dòng điện và điện áp cung cấp cho ống huỳnh quang.

+ Hạn chế tình trạng hỏng đèn do hồ quang xuất hiện gây tổng trở giảm.

+ Hạn chế dòng điện quá mức khi khởi động đèn.

- Tác dụng của tắc te: 

+ Giúp khởi động đèn bằng cách tạo ra một xung điện áp cao.

+ Sau khi đèn đã sáng, tắc te tự ngắt.

Câu hỏi tr 12 CH

Từ các dụng cụ thí nghiệm như Hình 1.14, đề xuất phương án thí nghiệm khảo sát mối liên hệ giữa điện áp hiệu dụng và cường độ dòng điện hiệu dụng trong mạch RLC nối tiếp theo các gợi ý sau:

- Cách bố trí thí nghiệm và các bước tiến hành thí nghiệm.

- Dự kiến kết quả cần thu thập và xử lí số liệu.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

- Tiến hành thí nghiệm:

+ Bước 1: Lắp mạch điện như sơ đồ Hình 1.15

+ Bước 2: Nối hai đầu đoạn mạch với đầu ra của biến áp nguồn để cấp dòng điện xoay chiều cho mạch.

+ Bước 3: Vặn núm xoay trên biến áp nguồn sao cho điện áp trên vôn kế lần lượt là 3 V, 6 V, 9 V, 12 V, 15 V, 18 V, 21 V.

- Kết quả: 

Câu hỏi tr 12 TN

Báo cáo kết quả thí nghiệm (số liệu minh hoạ)

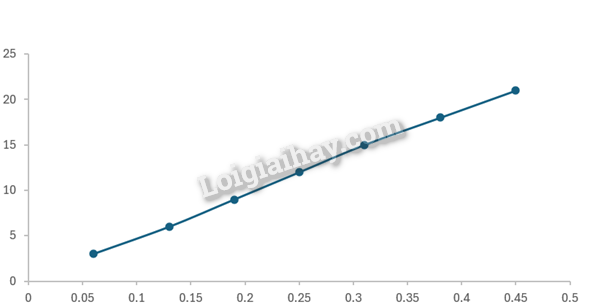
- Từ bảng số liệu, vẽ đồ thị mô tả sự phụ thuộc của I theo U trong mạch điện xoay chiều RLC mắc nối tiếp.

- Nhận xét về mối liên hệ của I và U từ đồ thị, so sánh với kết quả lí thuyết đã biết.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

- Đồ thị mô tả sự phụ thuộc của I theo U trong mạch điện xoay chiều RLC mắc nối tiếp.

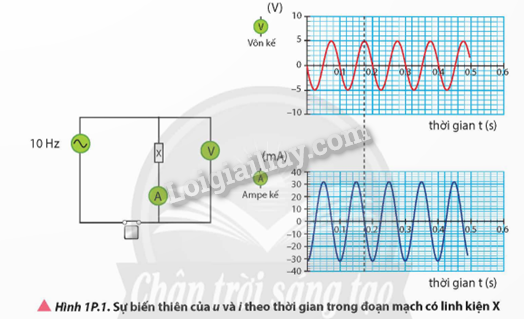
- Nhận xét: điện áp hiệu dụng càng lớn thì cường độ hiệu dụng càng tăng. Cường độ dòng điện tỉ lệ thuận với điện áp.

- Theo như lí thuyết thì: \(I = \frac{U}{Z}\), từ công thức này ta cũng thấy được rằng I tỉ lệ thuận với U. Vậy nên đồ thị mô tả sự phụ thuộc của I theo U trong mạch điện RLC nối tiếp cho thấy mối liên hệ tỉ lệ thuận giữa I và U phù hợp với kết quả lí thuyết đã biết.

Bài tập Bài 1

Mạch điện xoay chiều gồm điện trở thuần \(40\Omega \) ghép nối tiếp với một cuộn cảm thuẩn có độ tự cảm \(L = \frac{{0,4}}{\pi }H\). Biết biểu thức giữa điện áp hai đầu mạch là \(u = 80\cos 100\pi t(V)\). Cường độ dòng điện hiệu dụng chạy qua đoạn mạch là:

A. 1 A.             B. \(\sqrt 2 \)A.         C. \(\frac{1}{{\sqrt 2 }}\)A         D. 2 A

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

Ta có: \({Z_L} = \omega L = 100\pi .\frac{{0,4}}{\pi } = 40\Omega \)

\(Z = \sqrt {{R^2} + Z_L^2}  = \sqrt {{{40}^2} + {{40}^2}}  = 40\sqrt 2 \Omega \)

Cường độ dòng điện hiệu dụng chạy qua đoạn mạch là: 

\({I_0} = \frac{{{U_0}}}{Z} = \frac{{80}}{{40\sqrt 2 }} = \sqrt 2 A\)
\(I = \frac{{{I_0}}}{{\sqrt 2 }} = \frac{{\sqrt 2 }}{{\sqrt 2 }} = 1A\)

Đáp án A

Bài tập Bài 2

Hình 1P.1 biểu diễn sự biến thiên theo thời gian của điện áp và cường độ dòng điện xoay chiều qua một linh kiện X (X là một trong ba linh kiện R, L, C) thông qua phần mềm thí nghiệm mô phỏng.

a) Dựa vào đồ thị Hình 1P.1, viết biểu thức u, i theo thời gian.

b) Xác định độ lệch pha giữa điện áp và cường độ dòng điện, từ đó xác định tên linh kiện X.

c) Các thông số đặc trưng của linh kiện X.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

a) Biểu thức u là: \(u = 5\cos \left( {20\pi t + \frac{\pi }{2}} \right)V\)

Biểu thức I là: \(i = 32\cos \left( {20\pi t - \pi } \right)A\)

b) Độ lệch pha giữa điện áp và cường độ dòng điện là \(\frac{\pi }{2}\) mà điện áp trễ pha \(\frac{\pi }{2}\) so với cường độ dòng điện nên linh kiện X là tụ điện.

c) Các thông số đặc trưng của linh kiện X là:

Dung kháng: \({Z_C} = \frac{1}{{\omega C}}\)

Bài tập Bài 3

Điện áp xoay chiều có tần số 50 Hz vào hai đầu đoạn mạch gồm RLC nối tiếp gồm điện trở thuần \(150\Omega \), tụ điện có điện dung \(\frac{{200}}{\pi }\mu F\) và cuộn cảm thuần có độ tự cảm \(\frac{2}{\pi }H\). Cường độ dòng điện hiệu dung trong mạch là 1 A. Tính:

a) Tổng trở của toàn mạch.

b) Điện áp hiệu dụng đặt vào đoạn mạch.

Phương pháp giải:

Vận dụng lí thuyết về đặc trưng của dòng điện xoay chiều

Lời giải chi tiết:

a) Ta có: \({Z_L} = \omega L = 2\pi fL = 2\pi .50.\frac{2}{\pi } = 200\Omega \)

\({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}} = \frac{1}{{2\pi .50.\frac{{{{200.10}^{ - 6}}}}{\pi }}} = 50\Omega \)

Tổng trở toàn mạch là: \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}}  = \sqrt {{{150}^2} + {{(200 - 50)}^2}}  = 150\sqrt 2 \Omega \)

b) Điện áp hiệu dụng đặt vào đoạn mạch là:

\(I = \frac{{{I_0}}}{{\sqrt 2 }} \to {I_0} = I\sqrt 2  = \sqrt 2 A\)
\({I_0} = \frac{{{U_0}}}{Z} \to {U_0} = \sqrt 2 .150\sqrt 2  = 300V\)
\(u = \frac{{{U_0}}}{{\sqrt 2 }} = \frac{{300}}{{\sqrt 2 }} = 150\sqrt 2 V\)