Đề thi vào 10 môn Toán Quảng Ngãi năm 2020

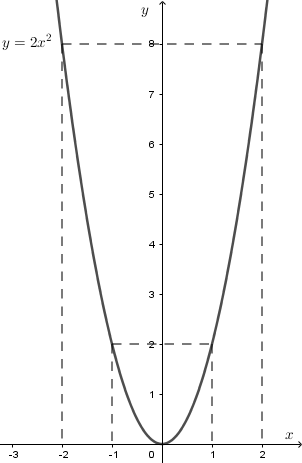
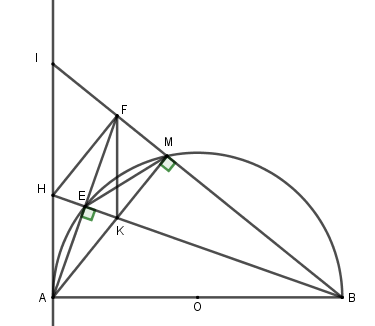
Đề bài

Câu 1:

1. Thực hiện phép tính \(16\sqrt 9  - 9\sqrt {16} \)

2. Cho hàm số \(y = a{x^2}\) , với \(a\) là tham số

a) Tìm \(a\) để đồ thị hàm số qua điểm \(M\left( {2;8} \right)\)

b) Vẽ đồ thị của hàm số ứng với giá trị \(a\) tìm được.

Câu 2:

1. Giải phương trình và hệ phương trình sau:

a) \({x^2} - 5x + 4 = 0\)

b)  \(\left\{ \begin{array}{l}3x + 2y = 8\\2x - y = 3\end{array} \right..\)

2. Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + m - 4 = 0\), với \(m\) là tham số

a) Chứng minh phương trình có hai nghiệm phân biệt với mọi \(m.\)

b) Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình. Chứng minh giá trị biểu thức \(A = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right)\) không phụ thuộc \(m\).

Câu 3:

Để chuẩn bị vào năm học mới, bạn An muốn mua một cái cặp và một đôi giày. Bạn đã tìm hiểu, theo giá niêm yết thì tổng số tiền để mua hai vật dụng trên là 850.000 đồng. Khi bạn An đến mua thì của hàng có chương trình giảm giá: cái cặp được giảm 15.000 đồng, đôi giày được giảm 10% so với giá niêm yết. Do đó bạn An mua hai vật dụng trên chỉ với số tiền 785.000 đồng. Hỏi giá niêm yết của mỗi vật dụng trên là bao nhiêu?

Câu 4:

Cho nửa đường tròn tâm O, đường kính AB và điểm M bất kì trên nửa đường tròn đó (với \(M \ne A\) và \(M \ne B\)). Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ tiếp tuyến Ax. Tía BM cắt Ax tại I, tia phân giác của góc \(\angle IAM\) cắt nửa đường tròn tại E và cắt tia BM tại F, tia BE cắt AM tại K và cắt Ax tại H.

a) Chứng minh tứ giác EFMK nội tiếp đường tròn.

b) Chứng minh ABF là tam giác cân.

c) Chứng minh tứ giác AKFH là hình thoi.

d) Xác định vị trí của điểm M để tứ giác AKFI nội tiếp được đường tròn.

Câu 5:

Cho hai số thực \(x;y\) thỏa mãn \(x + y = 5\) và \(xy =  - 2\) . Tính giá trị của biểu thức: \(P = \dfrac{{{x^3}}}{{{y^2}}} + \dfrac{{{y^3}}}{{{x^2}}} + 2020\)

Lời giải chi tiết

Câu 1 (2 điểm)

Cách giải:

1. Thực hiện phép tính \(16\sqrt 9  - 9\sqrt {16} \)

Ta có: \(16\sqrt 9  - 9\sqrt {16} \)\( = 16.3 - 9.4 = 48 - 36 = 12\)

2. Cho hàm số \(y = a{x^2}\) , với \(a\) là tham số

a) Tìm \(a\) để đồ thị hàm số qua điểm \(M\left( {2;8} \right)\)

Thay \(x = 2;y = 8\) vào hàm số \(y = a{x^2}\) ta được: \(8 = a{.2^2} \Leftrightarrow 4a = 8 \Leftrightarrow a = 2\)

Vậy \(a = 2\)

b) Vẽ đồ thị của hàm số ứng với giá trị \(a\) tìm được.

Với \(a = 2\) (câu a) ta có hàm số \(y = 2{x^2}.\)

Bảng giá trị:

Vậy đồ thị hàm số \(y = 2{x^2}\) là parabol đi qua 5 điểm \(\left( { - 2;8} \right);\left( { - 1;2} \right);\left( {0;0} \right);\left( {1;2} \right);\left( {2;8} \right)\)

Câu 2 (2 điểm)

Cách giải:

1. Giải phương trình và hệ phương trình sau:

a) \({x^2} - 5x + 4 = 0\)

\(\begin{array}{l} \Leftrightarrow {x^2} - x - 4x + 4 = 0\\ \Leftrightarrow x\left( {x - 1} \right) - 4\left( {x - 1} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right.\end{array}\)

Vậy phương trình có nghiệm \(x = 1;x = 4\)

b)  \(\left\{ \begin{array}{l}3x + 2y = 8\\2x - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 2y = 8\\4x - 2y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 14\\2x - y = 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 2\\2.2 - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)

Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2;1} \right)\)

2. Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + m - 4 = 0\), với \(m\) là tham số

a) Chứng minh phương trình có hai nghiệm phân biệt với mọi \(m.\)

Xét phương trình \({x^2} - 2\left( {m + 1} \right)x + m - 4 = 0\)

Ta có:

\(\begin{array}{l}\Delta ' = {\left[ { - \left( {m + 1} \right)} \right]^2} - 1.\left( {m - 4} \right)\\ = {m^2} + 2m + 1 - m + 4\\ = {m^2} + m + 5\end{array}\)

\(\begin{array}{l} = {m^2} + 2.m.\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{{19}}{4}\\ = {\left( {m + \dfrac{1}{2}} \right)^2} + \dfrac{{19}}{4}\end{array}\)

Vì \({\left( {m + \dfrac{1}{2}} \right)^2} \ge 0\) với mọi \(m\) nên \({\left( {m + \dfrac{1}{2}} \right)^2} + \dfrac{{19}}{4} \ge \dfrac{{19}}{4} > 0\) với mọi \(m\)

Hay \(\Delta ' > 0\) với mọi \(m\) nên phương trình đã cho có hai nghiệm phân biệt với mọi \(m.\)

b) Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình. Chứng minh giá trị biểu thức \(A = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right)\) không phụ thuộc \(m\).

Theo câu a) phương trình đã cho có hai nghiệm phân biệt với mọi \(m.\)

Gọi \({x_1};{x_2}\) là hai nghiệm của phương trình.

Theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2\\{x_1}{x_2} = m - 4\end{array} \right.\)

Ta có: \(A = {x_1}\left( {1 - {x_2}} \right) + {x_2}\left( {1 - {x_1}} \right)\)

\(\begin{array}{l} = {x_1} - {x_1}{x_2} + {x_2} - {x_1}{x_2}\\ = \left( {{x_1} + {x_2}} \right) - 2{x_1}{x_2}\\ = 2m + 2 - 2\left( {m - 4} \right)\\ = 2m + 2 - 2m + 8\\ = 10\end{array}\)

Vậy \(A = 10\) không phụ thuộc vào \(m.\)

Câu 3 (1,5 điểm)

Cách giải:

Để chuẩn bị vào năm học mới, bạn An muốn mua một cái cặp và một đôi giày. Bạn đã tìm hiểu, theo giá niêm yết thì tổng số tiền để mua hai vật dụng trên là 850.000 đồng. Khi bạn An đến mua thì của hàng có chương trình giảm giá: cái cặp được giảm 15.000 đồng, đôi giày được giảm 10% so với giá niêm yết. Do đó bạn An mua hai vật dụng trên chỉ với số tiền 785.000 đồng. Hỏi giá niêm yết của mỗi vật dụng trên là bao nhiêu?

Gọi giá niêm yết của một cái cặp bạn An muốn mua là: \(x\) (đồng), \(\left( {15\,\,000 < x < 850\,\,000} \right).\)

      Giá niêm yết của một đôi giày bạn An muốn mua là: \(y\) (đồng), \(\left( {0 < y < 850\,\,000} \right).\)

Giá niêm yết của một chiếc cặp và một đôi giày là \(850\,\,000\) đồng nên ta có phương trình:

\(x + y = 850\,\,000\,\,\,\left( 1 \right)\)

Giá của chiếc cặp sau khi giảm giá \(15\,\,000\) đồng là:\(x - 15\,\,000\) (đồng).

Giá của đôi giày sau khi giảm giá \(10\% \) là: \(y - 10\% y = \dfrac{9}{{10}}y\) (đồng).

Sau khi giảm giá bạn An trả tiền cho chiếc cặp và đôi giày là \(785\,\,000\) đồng nên ta có phương trình:

\(x - 15\,\,000 + \dfrac{9}{{10}}y = 785\,\,000\) \( \Leftrightarrow 10x + 9y = 8\,\,000\,\,000\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}x + y = 850\,\,\,000\\10x + 9y = 8\,\,000\,\,000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}10x + 10y = 8\,\,500\,\,000\\10x + 9y = 8\,\,000\,\,000\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 500\,\,000\\x = 850\,\,000 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 350\,\,000\,\,\,\,\left( {tm} \right)\\y = 500\,\,000\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy giá niêm yết bạn An mua một cặp sách là 350 000 đồng và một đôi giày là 500 000 đồng.

Câu 4 (3,5 điểm)

Cách giải:

Cho nửa đường tròn tâm O, đường kính AB và điểm M bất kì trên nửa đường tròn đó (với \(M \ne A\) và \(M \ne B\)). Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ tiếp tuyến Ax. Tía BM cắt Ax tại I, tia phân giác của góc \(\angle IAM\) cắt nửa đường tròn tại E và cắt tia BM tại F, tia BE cắt AM tại K và cắt Ax tại H.

a) Chứng minh tứ giác EFMK nội tiếp đường tròn.

Xét đường tròn \(\left( O \right)\) ta có:

\(\angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow \angle FEK = {90^0}\)

\(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow \angle FMK = {90^0}\)

Tứ giác EFMK có \(\angle FEK + \angle FMK = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\))

Vậy tứ giác EFMK nội tiếp đường tròn (đpcm).

b) Chứng minh ABF là tam giác cân.

Tứ giác AEMB nội tiếp nên \(\angle EAM = \angle EBM\) (cùng chắn cung EM)

Mà AF là tia phân giác của \(\angle IAM\) nên \(\angle IAF = \angle FAM = \angle EAM\)

\( \Rightarrow \angle EBM = \angle EBM = \angle FAI\)

Mà \(\angle FAI + \angle FAB = \angle IAB = {90^0}\)

\(\angle EBM + \angle EFB = {90^0}\)

Nên \(\angle FAB = \angle EFB = \angle AFB\).

Tam giác ABF có \(\angle FAB = \angle AFB\) nên là tam giác cân tại B (đpcm).

c) Chứng minh tứ giác AKFH là hình thoi.

Tam giác ABF cân tại B (câu b) nên \(BE\) vừa là đường cao vừa là đường trung tuyến.

\( \Rightarrow E\) là trung điểm AF.

Tam giác AHK có \(AE\) vừa là đường cao vừa là đường phân giác nên là tam giác cân tại \(A\)

\( \Rightarrow AE\) cũng là đường trung tuyến của tam giác

\( \Rightarrow E\) là trung điểm của HK.

Tứ giác AKFH có hai đường chéo AF, HK cắt nhau tại trung điểm của mỗi đường nên là hình bình hành.

Mà \(HK \bot AF\) nên tứ giác AKFH là hình thoi (dhnb) (đpcm).

d) Xác định vị trí của điểm M để tứ giác AKFI nội tiếp được đường tròn.

AKFH là hình thoi nên \(FK//AH \Rightarrow FK//AI\) nên tứ giác AKFI là hình thang.

Để tứ giác AKFI là tứ giác nội tiếp thì \(\angle AKF + \angle AIF = {180^0}\)

Mà \(\angle AKF + \angle KAI = {180^0}\) (kề bù)

Nên \(\angle AIF = \angle KAI\) hay \(\angle AIM = \angle MAI\)

Do đó tam giác \(AMI\) vuông cân \( \Rightarrow MAI = {45^0} \Rightarrow \angle MAB = {45^0}\)

\( \Rightarrow sd\,cung\,MB = 2\angle MAB = {2.45^0} = {90^0}\)

\( \Rightarrow M\) là điểm chính giữa cung AB.

Câu 5 (1 điểm)

Cách giải:

Cho hai số thực \(x;y\) thỏa mãn \(x + y = 5\) và \(xy =  - 2\) . Tính giá trị của biểu thức: \(P = \dfrac{{{x^3}}}{{{y^2}}} + \dfrac{{{y^3}}}{{{x^2}}} + 2020\)

Ta có:

\({x^2} + {y^2} = {\left( {x + y} \right)^2} - 2xy\) \( = {5^2} - 2.\left( { - 2} \right) = 29\)

\({x^3} + {y^3} = {\left( {x + y} \right)^3} - 3xy\left( {x + y} \right)\) \( = {5^3} - 3.\left( { - 2} \right).5 = 155\)

\(\begin{array}{l} \Rightarrow P = \dfrac{{{x^3}}}{{{y^2}}} + \dfrac{{{y^3}}}{{{x^2}}} + 2020 = \dfrac{{{x^5} + {y^5}}}{{{x^2}{y^2}}} + 2020\\ = \dfrac{{\left( {{x^2} + {y^2}} \right)\left( {{x^3} + {y^3}} \right) - \left( {{x^2}{y^3} + {x^3}{y^2}} \right)}}{{{{\left( {xy} \right)}^2}}} + 2020\\ = \dfrac{{\left( {{x^2} + {y^2}} \right)\left( {{x^3} + {y^3}} \right) - {x^2}{y^2}\left( {x + y} \right)}}{{{{\left( {xy} \right)}^2}}} + 2020\\ = \dfrac{{29.155 - {{\left( { - 2} \right)}^2}.5}}{{{{\left( { - 2} \right)}^2}}} + 2020\\ = \dfrac{{12555}}{4}.\end{array}\)

 Vậy \(P = \dfrac{{12555}}{4}\) .