Đề thi vào 10 môn Toán Phú Yên năm 2023

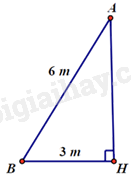
Đề bài

Phần I: Trắc nghiệm

Câu 1: Biểu thức \(\sqrt {{{(2 - \sqrt 3 )}^2}} \) có giá trị là

A. \(\sqrt 3 {\rm{ \;}} - 2\)

B. \(2 - \sqrt 3 \)

C. \(7 - 4\sqrt 3 \)

D. 1

Câu 2: Tìm \(x\) thỏa mãn biểu thức \(\sqrt {2 + \sqrt x } {\rm{ \;}} = 2\).

A. \(x = 0\)

B. \(x = \sqrt 2 \)

C. \(x = 2\)

D. \(x = 4\)

Câu 3: Hàm số nào sau đây không phải là hàm số bậc nhất?

A. \(y = 1 - x\).

B. \(y = \frac{x}{2}\).

C. \(y = \frac{2}{x}\).

D. \(y = \sqrt 2 (x - \sqrt 2 )\).

Câu 4: Đường thẳng \(y = {\rm{ \;}} - x + 3\) đi qua điểm \(M(m;1)\). Khi đó

A. \(m = 1\)

B. \(m = 2\)

C. \(m = 3\)

D. \(m = 4\)

Câu 5: Tìm các giá trị của \(a\) và \(b\) để hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ax - by = 2}\\{2ax + by = 1}\end{array}} \right.\) có nghiệm (1;-1).

A. \(a = 1,b = {\rm{ \;}} - 1\)

B. \(a = {\rm{ \;}} - 1,b = 1\)

C. \(a = 1,b = 1\)

D. \(a = 2,b = {\rm{ \;}} - 1\)

Câu 6: Cho m, n là nghiệm của phương trình \({x^2} + mx + n = 0\), với \(m \ne 0,n \ne 0\). Thế thì tổng các nghiệm của phương trình bằng

A. \( - 1\)

B.  1

C. \( - \frac{1}{2}\)

D. \(\frac{1}{2}\)

Câu 7: Một cái thang AB dài 6m tựa vào tường, chân thang cách tường 3m. Tính góc tạo bởi thang AB và tường AH.

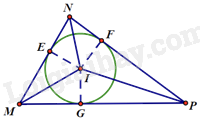
A. \(30^\circ \)

B. \(45^\circ \)

C. \(60^\circ \)

D. \(90^\circ \)

Câu 8: Tam giác nhọn MNP có đường tròn (I) nội tiếp, với E,F,G là các tiếp điểm. Khẳng định nào sau đây không đúng?

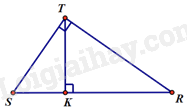
A. \(\angle IGP = 90^\circ \)

B. \(ME = MG\)

C. \(MNI = INP\)

D. N,I,G thẳng hàng

Câu 9: Cho tam giác STR vuông tại T, đường cao TK. Khẳng định nào sau đây sai?

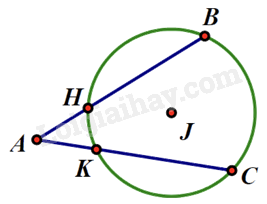
A. \(\frac{1}{{TK}} = \frac{1}{{TS}} + \frac{1}{{TR}}\)

B. \(S{R^2} = S{T^2} + T{R^2}\)

C. \(S{T^2} = SK.SR\)

D. \(TS \cdot TR = TK \cdot SR\)

Câu 10: Từ một điểm \(A\) ở ngoài đường tròn \((J)\), kẻ 2 cát tuyến AHB và AKC. Biết \(\angle BAC = 40^\circ \), các cung HB, BC, CK có cùng độ dài. Tìm số đo \(\angle HCK\).

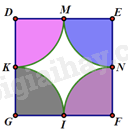
A. \(30^\circ \)

B. \(20^\circ \)

C. \(15^\circ \)

D. \(10^\circ \)

Câu 11: Hình vuông DEFG có cạnh bằng \(2\;cm;M,N,I,K\) là trung điểm các cạnh. Tính diện tích phần màu trắng giới hạn bởi 4 cung tròn KM, MN, NI, IK (tâm là các đỉnh hình vuông).

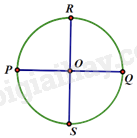
A. \(4 - \pi {\mkern 1mu} {\mkern 1mu} (c{m^2})\)

B. \(\pi {\rm{ \;}} - 4{\mkern 1mu} {\mkern 1mu} (c{m^2})\)

C. \(\pi {\mkern 1mu} {\mkern 1mu} (c{m^2})\)

D. \(4{\mkern 1mu} {\mkern 1mu} (c{m^2})\)

Câu 12: Đường tròn \((O)\) có bán kính bằng \(1\;cm\). Hai đường kính PQ và RS vuông góc nhau. Tính độ dài cung lớn PR.

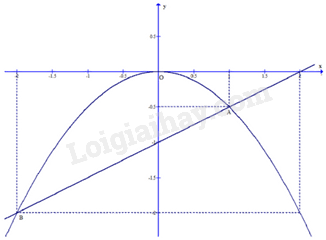
A. \(\frac{\pi }{4}(\;cm)\)

B. \(\frac{\pi }{2}(\;cm)\)

C. \(\frac{{3\pi }}{4}(\;cm)\)

D. \(\frac{{3\pi }}{2}(\;cm)\)

Phần II. Tự luận

Câu 13: Giải các phương trình, hệ phương trình sau:

а) \(2{x^2} + 5x + 2 = 0\);

b) \(\left\{ {\begin{array}{*{20}{l}}{xy = {\rm{ \;}} - 3}\\{3x + 3y + 2xy = 0}\end{array}} \right.\)

Câu 14: Cho hai hàm số \(y = {\rm{ \;}} - \frac{1}{2}{x^2}\) và \(y = ax + b\).

a) Tìm các hệ số a, b biết đường thẳng \(y = ax + b\) đi qua điểm \(M( - 2; - 2),N(4;1)\).

b) Với các giá trị a, b vừa tìm được, hãy:

- Tìm giao điểm của đường thẳng \(y = ax + b\) và đồ thị hàm số \(y = {\rm{ \;}} - \frac{1}{2}{x^2}\) bằng phương pháp đại số.

- Vẽ đồ thị hai hàm số \(y = {\rm{ \;}} - \frac{1}{2}{x^2}\) và \(y = ax + b\) trên cùng một mặt phẳng tọa độ.

Câu 15: Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.

Một khu đất hình chữ nhật có tỷ số hai kích thước là \(\frac{2}{3}\). Người ta làm một sân bóng đá mini 5 người ở giữa, chừa lối đi xung quanh (lối đi thuộc khu đất). Lối đi rộng 2m và có diện tích \(224\;{m^2}\). Tính các kích thước của khu đất.

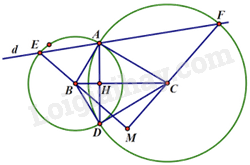
Câu 16: Cho tam giác ABC vuông tại \(A\), có \(AB = 3\;{\rm{cm}},AC = 4\;{\rm{cm}}\). Đường tròn tâm \(B\) bán kính BA và đường tròn tâm \(C\) bán kính CA cắt nhau tại điểm thứ hai \(D\).

a) Chứng minh tứ giác ABDC nội tiếp được.

b) Tính độ dài đoạn AD.

c) Một đường thẳng \(d\) quay quanh \(A\) cắt \((B)\) tại \(E(E \ne A)\) và cắt \((C)\) tại \(F(F \ne A)\). Gọi \(M\) là giao điểm của EB và FC. Khi \(d\) thay đổi thì điểm \(M\) chạy trên đường nào?

----- HẾT -----

Lời giải chi tiết

Phần I: Trắc nghiệm

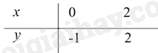
Câu 1 (NB):

Phương pháp:

\(\sqrt {{A^2}} {\rm{ \;}} = \left| A \right|\)

Cách giải:

\(\sqrt {{{(2 - \sqrt 3 )}^2}} \)\( = 2 - \sqrt 3 \)

Chọn B.

Câu 2 (NB):

Phương pháp:

Giải phương trình chứa căn. Bình phương hai vế.

Cách giải:

ĐKXĐ: \(\sqrt x {\rm{ \;}} \ge 0 \Leftrightarrow x \ge 0\)

\(\begin{array}{*{20}{l}}{\sqrt {2 + \sqrt x } {\rm{ \;}} = 2}\\{ \Leftrightarrow 2 + \sqrt x {\rm{ \;}} = 4}\\{ \Leftrightarrow \sqrt x {\rm{ \;}} = 2}\end{array}\)

\( \Leftrightarrow x = 4\) (tmđk)

Chọn D.

Câu 3 (NB):

Phương pháp:

Hàm số bậc nhất là hàm số được cho bởi công thức \(y = ax + b\) trong đó \(a,{\mkern 1mu} {\mkern 1mu} b\) là các số thực cho trước và \(a \ne 0\)

Cách giải:

Hàm số \(y = \frac{2}{x}\) không phải là hàm số bậc nhất.

Chọn C.

Câu 4 (NB):

Phương pháp:

Thay \(M(m;1)\) vào đường thẳng \(y = {\rm{ \;}} - x + 3\)

Cách giải:

Thay \(M(m;1)\) vào đường thẳng \(y = {\rm{ \;}} - x + 3\), ta được:

\(\begin{array}{*{20}{l}}{1 = {\rm{ \;}} - m + 3}\\{m = 3 - 1 = 2}\end{array}\)

Chọn B.

Câu 5 (NB):

Phương pháp:

Thay nghiệm (1;-1) vào hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ax - by = 2}\\{2ax + by = 1}\end{array}} \right.\).

Cách giải:

Thay nghiệm (1;-1) vào hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{ax - by = 2}\\{2ax + by = 1}\end{array}} \right.\) ta được:

\(\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{a \cdot 1 - b \cdot ( - 1) = 2}\\{2a \cdot 1 + b \cdot ( - 1) = 1}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a + b = 2}\\{2a - b = 1}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3a = 3}\\{a + b = 2}\end{array}} \right.}\\{ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 1}\end{array}} \right.}\end{array}\)

Chọn C.

Câu 6 (NB):

Phương pháp:

Áp dụng định lí viet

Cách giải:

Theo hệ thức Viet, ta có:

\(\left\{ {\begin{array}{*{20}{l}}{m + n = {\rm{ \;}} - m}\\{m \cdot n = n}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{n = {\rm{ \;}} - 2m}\\{m \cdot ( - 2m) = {\rm{ \;}} - 2m}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{n = {\rm{ \;}} - 2m}\\{\left[ {\begin{array}{*{20}{l}}{m = 1}\\{m = 0}\end{array}} \right.}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\left\{ {\begin{array}{*{20}{l}}{m = 1}\\{n = {\rm{ \;}} - 2}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{l}}{m = 0}\\{n = 0}\end{array}} \right.}\end{array}} \right.\)

Vậy tổng nghiệm của phương trình là \( - 1\)

Chọn A.

Câu 7 (NB):

Phương pháp:

Áp dụng công thức lượng giác.

Cách giải:

\(A{B^2} = A{H^2} + B{H^2}\) (Pytago)

\(\begin{array}{*{20}{l}}{ \Rightarrow A{H^2} = A{B^2} - B{H^2}}\\{ \Rightarrow AH = \sqrt {A{B^2} - B{H^2}} {\rm{ \;}} = \sqrt {{6^2} - {3^2}} {\rm{ \;}} = 3\sqrt 3 }\end{array}\)

\(\sin \angle BAH = \frac{3}{{3\sqrt 3 }} = \frac{{\sqrt 3 }}{3} \Rightarrow \angle BAH = 30^\circ \)

Chọn A.

Câu 8 (TH):

Phương pháp:

Áp dụng tính chất đường tròn nội tiếp tam giác.

Tâm của đường tròn nội tiếp tam giác là giao điểm giữa 3 đường phân giác của tam giác đó do đó bán kính của đường tròn nội tiếp tam giác chính bằng khoảng cách từ tâm hạ vuông góc xuống ba cạnh của tam giác.

Cách giải:

Áp dụng tính chất đường tròn nội tiếp tam giác.

Tâm của đường tròn nội tiếp tam giác là giao điểm giữa 3 đường phân giác của tam giác đó do đó bán kính của đường tròn nội tiếp tam giác chính bằng khoảng cách từ tâm hạ vuông góc xuống ba cạnh của tam giác.

Suy ra A,C đúng.

Xét \(\Delta MEI\) và \(\Delta MGI\) có:

MI chung

\(\angle MEI = \angle IGM = 90^\circ \)

\(\angle EMI = \angle IMG\) (MI là đường phân giác)

Vậy \(\Delta MEI = \Delta MGI\) (g.c.g)

Suy ra ME = MG . Suy ra B đúng

Vậy D sai.

Chọn D.

Câu 9 (NB):

Phương pháp:

Áp dụng công thức tính đường cao trong tam giác vuông.

Cách giải:

Tam giác STRvuông tại \(T\), đường cao TK ta có:

\(\frac{1}{{T{K^2}}} = \frac{1}{{T{S^2}}} + \frac{1}{{T{R^2}}}\). Vậy A sai.

Chọn A.

Câu 10 (TH):

Phương pháp:

Áp dụng tổng các góc trong một tam giác bằng \(180^\circ .\)

Cách giải:

Ta có HB = BC = CK

Vì AB, AC là cát tuyến của đường tròn \((J)\) mà HB = HC nên AB = AC.

\(\begin{array}{*{20}{l}}{ \Rightarrow \angle ABC = \angle ACB = \frac{{180^\circ {\rm{ \;}} - 40^\circ }}{2} = 70^\circ }\\{{\rm{Ta}}{\mkern 1mu} {\mkern 1mu} {\rm{c\'o }}:HB = BC \Rightarrow \angle BHC = \angle BCH = \frac{{180^\circ {\rm{ \;}} - \angle HBC}}{2}}\\{ \Rightarrow \angle BHC = \frac{{180^\circ {\rm{ \;}} - \angle ACB}}{2} = 55^\circ {\rm{ \;}} = \angle BCH}\end{array}\)

Mà \(\angle ACB = \frac{{180^\circ {\rm{ \;}} - 40^\circ }}{2} = 70^\circ {\rm{ \;}} \Rightarrow \angle HCK = 70^\circ {\rm{ \;}} - 55^\circ {\rm{ \;}} = 15^\circ \).

Chọn C.

Câu 11 (VD):

Phương pháp:

Diện tích phần màu trắng bằng diện tích hình vuông trừ diện tích của 4 cung tròn.

Diện tích cung tròn được tính bằng \(S = \frac{{\pi {R^2}n}}{{360}}\).

Cách giải:

Ta có D là tâm của đường tròn chứa cung KM, đường kính DM = 1 cm

Ta có số đo cung KM  là \(90^\circ \)

\( \Rightarrow \) Diện tích cung tròn là \(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.1}^2}.90}}{{360}} = \frac{1}{4}\pi (c{m^2})\)

Vì DEFG là hình vuông, M, N, I, K là trung điểm các cạnh nên diện tích số đo của 4 cung tròn KM, MN, NI, IK là bằng nhau.

Diện tích hình vuông là: \(S = 2.2 = 4(c{m^2})\)

Vậy diện tích phần màu trắng là: \(S = 4 - \frac{1}{4}\pi .4 = 4 - \pi {\mkern 1mu} {\mkern 1mu} (c{m^2})\).

Chọn A.

Câu 12 (TH):

Phương pháp:

Diện tích cung tròn được tính bằng \(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{lR}}{2}\).

Cách giải:

Ta có số đo cung lớn PR  là \(270^\circ \)

\( \Rightarrow \) Diện tích cung tròn là \(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.1}^2}.270}}{{360}} = \frac{3}{4}\pi (c{m^2})\)

\( \Leftrightarrow \)\(\frac{3}{4}\pi {\rm{ \;}} = \frac{{lR}}{2} \Leftrightarrow \frac{3}{4}\pi {\rm{ \;}} = \frac{{l.1}}{2} \Rightarrow l = \frac{3}{2}\pi {\mkern 1mu} {\mkern 1mu} (cm)\)

Chọn D.

Phần II. Tự luận

Câu 13 (TH):

Phương pháp:

a) Tính \(\Delta \).

b) Giải hệ phương trình bằng phương pháp thế.

Cách giải:

a) Ta có: \(\Delta {\rm{ \;}} = {5^2} - 4 \cdot 2 \cdot 2 = 9 = {3^2} > 0\) nên phương trình có 2 nghiệm:\({x_1} = \frac{{ - 5 + 3}}{{2.2}} = {\rm{ \;}} - \frac{1}{2},{x_2} = \frac{{ - 5 - 3}}{{2.2}} = {\rm{ \;}} - 2.\)

Vậy tập nghiệm của phương trình là \(S = \left\{ { - \frac{1}{2}; - 2} \right\}\).

b) \(\left\{ {\begin{array}{*{20}{l}}{xy = {\rm{ \;}} - 3{\rm{ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}}({\rm{1}})}\\{3x + 3y + 2xy = 0{\rm{ \;\;}}({\rm{2}})}\end{array}} \right.\)

Thế (1) vào (2) ta được: \(x + y = 2\). Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{xy = {\rm{ \;}} - 3}\\{x + y = 2}\end{array}} \right.\)

Do đó x, y là nghiệm của phương trình \({X^2} - 2X - 3 = 0\).

Giải phương trình này ta được nghiệm: \({X_1} = {\rm{ \;}} - 1;{X_2} = 3\).

Vậy hệ phương trình trên có hai cặp nghiệm: \(\left\{ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 1}\\{y = 3}\end{array}} \right.\) và \(\left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = {\rm{ \;}} - 1}\end{array}} \right.\)

Câu 14 (VD):

Phương pháp:

a) Thay tọa độ điểm \(M( - 2; - 2),N(4;1)\) vào đường thẳng.

b) Xét phương trình hoành độ giao điểm.

Cách giải:

a) Vì đường thẳng \(y = ax + b\) đi qua điểm \(M( - 2; - 2),N(4;1)\) nên khi thế tọa độ các điểm M,Nvào hàm số \(y = ax + b\) ta có hệ phương trình:

\(\left\{ {\begin{array}{*{20}{l}}{1 = 4a + b}\\{ - 2 = {\rm{ \;}} - 2a + b}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3 = 6a}\\{1 = 4a + b}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{1}{2}}\\{b = 1 - 4.\frac{1}{2} = {\rm{ \;}} - 1}\end{array}} \right.\)

Vậy hệ phương trình có nghiệm \(\left\{ {\begin{array}{*{20}{l}}{a = \frac{1}{2}}\\{b = {\rm{ \;}} - 1}\end{array}} \right.\).

b) Với \(a = \frac{1}{2},b = {\rm{ \;}} - 1\), đường thẳng \(y = ax + b\) là \(y = \frac{x}{2} - 1\).

Phương trình hoành độ giao điểm của đường thẳng \(y = \frac{x}{2} - 1\) và đồ thị hàm số \(y = {\rm{ \;}} - \frac{1}{2}{x^2}\) là: \( - \frac{1}{2}{x^2} = \frac{x}{2} - 1\)

\( \Leftrightarrow {x^2} + x - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = {\rm{ \;}} - 2}\end{array}} \right.\)

Với \(x = 1 \Rightarrow y = {\rm{ \;}} - \frac{1}{2}\), ta có giao điểm \(A\left( {1; - \frac{1}{2}} \right)\); với \(x = {\rm{ \;}} - 2 \Rightarrow y = {\rm{ \;}} - 2\), ta có giao điểm \(B( - 2; - 2)\).

c) Hàm số \(y = {\rm{ \;}} - \frac{1}{2}{x^2}\) có bảng giá trị:

Hàm số \(y = \frac{x}{2} - 1\) có bảng giá trị:

Đồ thị:

Câu 15 (VD):

Phương pháp:

Gọi \(x,y(m)\) lần lượt là 2 kích thước của khu đất \((x > y > 0)\).

Dựa vào đề bài lập các phương trình có liên quan.

Cách giải:

Gọi \(x,y(m)\) lần lượt là 2 kích thước của khu đất \((x > y > 0)\).

Theo đề bài, tỷ số hai kích thước là \(\frac{2}{3}\) nên ta có phương trình thứ nhất:

\(\frac{y}{x} = \frac{2}{3} \Leftrightarrow 2x - 3y = 0.\)

Vì lối đi rộng \(2\;m\) có diện tích \(224\;{m^2}\) nên ta có phương trình thứ hai:

\(2x.2 + 2(y - 4).2 = 224 \Leftrightarrow x + y = 60.\)

Ta có hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{2x - 3y = 0}\\{x + y = 60}\end{array}} \right.\)

Giải hệ phương trình ta được \(\left\{ {\begin{array}{*{20}{l}}{x = 36}\\{y = 24}\end{array}} \right.\).

Vậy, khu đất có chiều rộng \(24\;m\), chiều dài \(36\;m\).

Câu 16 (VDC):

Phương pháp:

Áp dụng các tính chất hình học để chứng minh.

Cách giải:

a) Xét hai tam giác ABC và DBC có:

\(AB = DB = 3(\;cm);AC = DC = 4(\;cm);BC\) chung;

Suy ra \(\Delta ABC = \Delta DBC\) (c-c-c)

Suy ra \(\angle BAC = \angle BDC = 90^\circ {\rm{\;}} \Rightarrow \angle BAC + \angle BDC = 180^\circ \).

Vậy ABDC là tứ giác nội tiếp.

b) Gọi \(H\) là giao điểm của BC với AD; khi đó \(BC \bot AD\) hay AH là đường cao \(\Delta ABC\).

Áp dụng hệ thức lượng tam giác vuông vào \(\Delta ABC\) ta có:

\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} \Leftrightarrow AH = \frac{{AB \cdot AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \frac{{3.4}}{{\sqrt {{3^3} + {4^2}} }} = \frac{{12}}{5}.\)

Do đó, \(AD = 2AH = 2 \cdot \frac{{12}}{5} = \frac{{24}}{5}(\;cm)\).

c) Trong \(\Delta MEF\) có: \(\angle EMF + \angle MEF + \angle MFE = 180^\circ (1)\).

\(\Delta BAE\) cân tại \(B(BA = BE)\) suy ra \(\angle BEA = \angle BAE\) (2). Tương tự, \(\angle CFA = \angle CAF\) (3).

Ta có: \(\angle BAE + \angle BAC + \angle CAF = 180^\circ \) (4). Kết hợp (1), (2), (3) và (4) suy ra \(\angle BMC = 90^\circ \).

Khi \(d\) thay đổi quanh \(A\), điểm \(M\) luôn nhìn đoạn thẳng BC cố định dưới 1 góc vuông nên \(M\) chạy trên đường tròn đường kính BC.

-----HẾT-----