Đề thi vào 10 môn Toán Lào Cai năm 2020Tải vềCâu 1: Tính
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
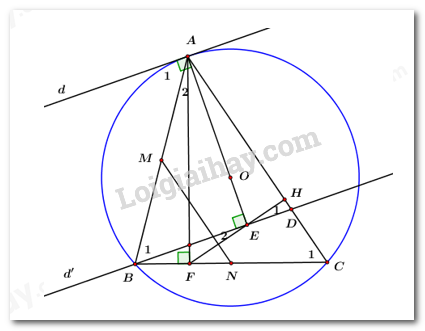
Đề bài Câu 1: Tính a) \(\sqrt {16} + 1\) b) \(\sqrt 3 .\sqrt {12} \) Câu 2: Cho biểu thức \(P = \left( {\dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{\sqrt x - 1}}} \right).\dfrac{{x - 1}}{{2\sqrt x + 1}}\) (với \(x \ge 0,\,\,x \ne 1\)). a) Rút gọn biểu thức \(P\). b) Tìm tất cả các giá trị của \(x\) để \(P \le - 1\). Câu 3: a) Xác định hàm số \(y = a{x^2}\) biết rằng đồ thị của hàm số đi qua điểm \(A\left( { - 2;5} \right)\). b) Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d:y = \dfrac{{m - 1}}{m}x - m + 1,\) với \(m \ge \dfrac{3}{2}\). Tìm \(m\) để \(d\) cắt trục tung, trục hoành lần lượt tại hai điểm phân biệt \(A,B\) sao cho độ dài đoạn \(AB\) ngắn nhất. Câu 4: 4.1) Giải hệ phương trình \(\left\{ \begin{array}{l}2x - 3y = - 4\\ - x + 3y = 5\end{array} \right..\) 4.2) Lúc 8 giờ người thứ nhất đi xe máy từ \(A\) với vận tốc \(40\,km/h.\) Sau đó 2 giờ, người thứ hai đi ô tô cũng từ \(A\) với vận tốc \(60\,km/h\) đuổi theo người thứ nhất. Hỏi hai người gặp nhau vào lúc mấy giờ? 4.3. a) Giải phương trình \(2{x^2} - 5x + 3 = 0\). b) Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 6 = 0\) có hai nghiệm \({x_1},\,\,{x_2}\) sao cho \(x_1^2 + 4{x_1} + 2{x_2} - 2m{x_1} = - 3\). Câu 5: Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O.\) Kẻ đường thẳng \(d\) là tiếp tuyến tại \(A\) của đường tròn \(\left( O \right)\). Gọi \(d'\) là đường thẳng qua \(B\) và song song với \(d\); \(d'\) cắt các đường thẳng \(AO,AC\) lần lượt tại \(E,D\). Kẻ \(AF\) là đường cao của tam giác \(ABC\) (\(F\) thuộc \(BC\)). a) Chứng minh rằng tứ giác ABFE nội tiếp. b) Chứng minh rằng \(A{B^2} = AD.AC\). c) Gọi M, N lần lượt là trung điểm của AB, BC. Chứng minh rằng \(MN\) vuông góc với \(EF\). Lời giải Câu 1 (1 điểm) Cách giải: Tính a) \(\sqrt {16} + 1\) Ta có: \(\sqrt {16} + 1\)\( = 4 + 1 = 5\). b) \(\sqrt 3 .\sqrt {12} \) Ta có \(\sqrt 3 .\sqrt {12} = \sqrt {3.12} = \sqrt {36} = 6\). Câu 2 (1,5 điểm) Cách giải: Cho biểu thức \(P = \left( {\dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{\sqrt x - 1}}} \right).\dfrac{{x - 1}}{{2\sqrt x + 1}}\) (với \(x \ge 0,\,\,x \ne 1\)). a) Rút gọn biểu thức \(P\). Với \(x \ge 0,\,\,x \ne 1\) ta có: \(\begin{array}{l}\,\,\,\,\,\,P = \left( {\dfrac{1}{{\sqrt x + 1}} - \dfrac{1}{{\sqrt x - 1}}} \right).\dfrac{{x - 1}}{{2\sqrt x + 1}}\\ \Leftrightarrow P = \dfrac{{\sqrt x - 1 - \sqrt x - 1}}{{\left( {\sqrt x + 1} \right).\left( {\sqrt x - 1} \right)}}.\dfrac{{x - 1}}{{2\sqrt x + 1}}\\ \Leftrightarrow P = \dfrac{{ - 2}}{{x - 1}}.\dfrac{{x - 1}}{{2\sqrt x + 1}}\\ \Leftrightarrow P = \dfrac{{ - 2}}{{2\sqrt x + 1}}\end{array}\) Vậy với \(x \ge 0,\,\,x \ne 1\) thì \(P = - \dfrac{2}{{2\sqrt x + 1}}\). b) Tìm tất cả các giá trị của \(x\) để \(P \le - 1\). Với \(x \ge 0,\,\,x \ne 1\) ta có: \(\begin{array}{l}\,\,\,\,\,P \le - 1\\ \Leftrightarrow \dfrac{{ - 2}}{{2\sqrt x + 1}} \le - 1\\ \Leftrightarrow \dfrac{{ - 2}}{{2\sqrt x + 1}} + 1 \le 0\\ \Leftrightarrow \dfrac{{ - 2 + 2\sqrt x + 1}}{{2\sqrt x + 1}} \le 0\\ \Leftrightarrow \dfrac{{2\sqrt x - 1}}{{2\sqrt x + 1}} \le 0\end{array}\) Do \(2\sqrt x + 1 \ge 1 > 0\,\,\forall x \ge 0,\,\,x \ne 1\) nên \(\dfrac{{2\sqrt x - 1}}{{2\sqrt x + 1}} \le 0 \Leftrightarrow 2\sqrt x - 1 \le 0\)\( \Leftrightarrow \sqrt x \le \dfrac{1}{2} \Leftrightarrow x \le \dfrac{1}{4}\) Kết hợp điều kiện \(x \ge 0,\,\,x \ne 1\) ta có: \(0 \le x \le \dfrac{1}{4}\). Vậy với \(0 \le x \le \dfrac{1}{4}\) thì \(P \le - 1\). Câu 3 (1 điểm) Cách giải: a) Xác định hàm số \(y = a{x^2}\) biết rằng đồ thị của hàm số đi qua điểm \(A\left( { - 2;5} \right)\). Vì đồ thị của hàm số \(y = a{x^2}\) đi qua điểm \(A\left( { - 2;5} \right)\) nên ta có: \(5 = a.{\left( { - 2} \right)^2} \Leftrightarrow a = \dfrac{5}{4}\). Vậy \(y = \dfrac{5}{4}{x^2}\). b) Trong mặt phẳng tọa độ \(Oxy\), cho đường thẳng \(d:y = \dfrac{{m - 1}}{m}x - m + 1,\) với \(m \ge \dfrac{3}{2}\). Tìm \(m\) để \(d\) cắt trục tung, trục hoành lần lượt tại hai điểm phân biệt \(A,B\) sao cho độ dài đoạn \(AB\) ngắn nhất. Với \(m \ge \dfrac{3}{2}\) ta có: Giao điểm của đường thẳng \(d\) và trục tung là \(A\left( {0;y} \right)\). Vì \(A\left( {0;y} \right) \in d\) nên \(y = \dfrac{{m - 1}}{m}.0 - m + 1 = 1 - m\). Suy ra \(A\left( {0;1 - m} \right)\). Giao điểm của đường thẳng \(d\) và trục hoành là \(B\left( {x;0} \right)\). Vì \(B\left( {x;0} \right) \in d\) nên \(0 = \dfrac{{m - 1}}{m}.x - m + 1\)\( \Leftrightarrow \dfrac{{m - 1}}{m}x = m - 1 \Leftrightarrow x = m\) (vì \(m \ge \dfrac{3}{2}\)). Suy ra \(B\left( {m;0} \right)\). Với \(m \ge \dfrac{3}{2}\) ta có: \(A\left( {0;1 - m} \right) \Leftrightarrow OA = \left| {1 - m} \right| = m - 1\). \(B\left( {m;0} \right) \Leftrightarrow OB = \left| m \right| = m\) Xét tam giác \(OAB\) vuông tại \(O\), theo định lý Pytago ta có: \(A{B^2} = O{A^2} + O{B^2}\) \( = {\left( {m - 1} \right)^2} + {m^2} = 2{m^2} - 2m + 1\)\( = 2\left( {{m^2} - m + \dfrac{1}{4}} \right) + \dfrac{1}{2} = 2{\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{1}{2}\). Vì \(m \ge \dfrac{3}{2}\) nên \({\left( {m - \dfrac{1}{2}} \right)^2} \ge {\left( {\dfrac{3}{2} - \dfrac{1}{2}} \right)^2} \Leftrightarrow {\left( {m - \dfrac{1}{2}} \right)^2} \ge 1\). \( \Rightarrow 2{\left( {m - \dfrac{1}{2}} \right)^2} + \dfrac{1}{2} \ge 2.1 + \dfrac{1}{2} = \dfrac{5}{2}\). Ta có: \(A{B^2}\) nhỏ nhất bằng \(\dfrac{5}{2} \Leftrightarrow m = \dfrac{3}{2}\). Vậy độ dài \(AB\) nhỏ nhất là \(\dfrac{{\sqrt {10} }}{2}\) \( \Leftrightarrow m = \dfrac{3}{2}\). Câu 4 (3,5 điểm) Cách giải: 4.1) Giải hệ phương trình \(\left\{ \begin{array}{l}2x - 3y = - 4\\ - x + 3y = 5\end{array} \right..\) \(\left\{ \begin{array}{l}2x - 3y = - 4\\ - x + 3y = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\3y = x + 5\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\3y = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\) Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\,\,y} \right) = \left( {1;\,\,2} \right).\) 4.2) Lúc 8 giờ người thứ nhất đi xe máy từ \(A\) với vận tốc \(40\,km/h.\) Sau đó 2 giờ, người thứ hai đi ô tô cũng từ \(A\) với vận tốc \(60\,km/h\) đuổi theo người thứ nhất. Hỏi hai người gặp nhau vào lúc mấy giờ? Gọi quãng đường cả hai người đi đến lúc gặp nhau là \(x\,\,\left( {km} \right),\,\,\left( {x > 0} \right).\) Khi đó thời gian người thứ nhất đi đến lúc gặp người thứ hai là: \(\dfrac{x}{{40}}\,\,\left( h \right).\) Thời gian người thứ hai đi đến lúc gặp người thứ nhất là: \(\dfrac{x}{{60}}\,\,\left( h \right).\) Người thứ hai đi sau người thứ nhất 2 giờ nên ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{x}{{40}} - \dfrac{x}{{60}} = 2\\ \Leftrightarrow 3x - 2x = 240\\ \Leftrightarrow x = 240\,\,\,\left( {tm} \right)\end{array}\) \( \Rightarrow \) Thời gian người thứ nhất đi đến khi gặp người thứ hai là: \(\dfrac{{240}}{{40}} = 6\,\,\left( h \right).\) Vậy hai người gặp nhau lúc \(8 + 6 = 14\) giờ. 4.3. a) Giải phương trình \(2{x^2} - 5x + 3 = 0\). Ta có: \(\Delta = {\left( { - 5} \right)^2} - 4.2.3 = 1 > 0\), do đó phương trình \(2{x^2} - 5x + 3 = 0\) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{5 + 1}}{{2.2}} = \dfrac{3}{2}\\{x_2} = \dfrac{{5 - 1}}{{2.2}} = 1\end{array} \right.\). Vậy tập nghiệm của phương trình là \(S = \left\{ {\dfrac{3}{2};1} \right\}\). b) Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} - 2\left( {m - 1} \right)x + {m^2} - 6 = 0\) có hai nghiệm \({x_1},\,\,{x_2}\) sao cho \(x_1^2 + 4{x_1} + 2{x_2} - 2m{x_1} = - 3\). Để phương trình đã cho có 2 nghiệm \({x_1},\,\,{x_2}\) thì: \(\begin{array}{l}\Delta ' = {\left( {m - 1} \right)^2} - \left( {{m^2} - 6} \right) \ge 0\\ \Leftrightarrow {m^2} - 2m + 1 - {m^2} + 6 \ge 0\\ \Leftrightarrow - 2m + 7 \ge 0\\ \Leftrightarrow 2m \le 7\\ \Leftrightarrow m \le \dfrac{7}{2}\end{array}\) Khi đó áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m - 1} \right) = 2m - 2\\{x_1}{x_2} = {m^2} - 6\end{array} \right.\). Theo bài ra ta có: \(\begin{array}{l}\,\,\,\,\,\,x_1^2 + 4{x_1} + 2{x_2} - 2m{x_1} = - 3\\ \Leftrightarrow x_1^2 - 2\left( {m - 1} \right){x_1} + {m^2} - 6 + 2{x_1} + 2{x_2} = {m^2} - 6 - 3\\ \Leftrightarrow x_1^2 - 2\left( {m - 1} \right){x_1} + {m^2} - 6 + 2\left( {{x_1} + {x_2}} \right) = {m^2} - 9\,\,\left( * \right)\end{array}\) Vì \({x_1}\) là nghiệm của phương trình đã cho nên \(x_1^2 - 2\left( {m - 1} \right){x_1} + {m^2} - 6 = 0\), do đó \(\begin{array}{l}\left( * \right) \Leftrightarrow 2\left( {{x_1} + {x_2}} \right) = {m^2} - 9\\\,\,\,\,\,\,\, \Leftrightarrow 2.\left( {2m - 2} \right) = {m^2} - 9\\\,\,\,\,\,\, \Leftrightarrow 4m - 4 = {m^2} - 9\\\,\,\,\,\,\, \Leftrightarrow {m^2} - 4m - 5 = 0\\\,\,\,\,\,\, \Leftrightarrow {m^2} + m - 5m - 5 = 0\\\,\,\,\,\,\, \Leftrightarrow m\left( {m + 1} \right) - 5\left( {m + 1} \right) = 0\\\,\,\,\,\,\, \Leftrightarrow \left( {m + 1} \right)\left( {m - 5} \right) = 0\\\,\,\,\,\,\, \Leftrightarrow \left[ \begin{array}{l}m + 1 = 0\\m - 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 1\,\,\left( {tm} \right)\\m = 5\,\,\,\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy \(m = - 1\). Câu 5 (3 điểm) Cách giải: Cho tam giác \(ABC\) có ba góc nhọn \(\left( {AB < AC} \right)\) nội tiếp đường tròn tâm \(O.\) Kẻ đường thẳng \(d\) là tiếp tuyến tại \(A\) của đường tròn \(\left( O \right)\). Gọi \(d'\) là đường thẳng qua \(B\) và song song với \(d\); \(d'\) cắt các đường thẳng \(AO,AC\) lần lượt tại \(E,D\). Kẻ \(AF\) là đường cao của tam giác \(ABC\) (\(F\) thuộc \(BC\)).
a) Chứng minh rằng tứ giác ABFE nội tiếp. Ta có: \(AF \bot BC \Rightarrow \angle AFB = {90^0}\) \(\left\{ \begin{array}{l}OA \bot d\\d'//d\end{array} \right. \Rightarrow OA \bot d' \Rightarrow \angle AEB = {90^0}\) Tứ giác \(ABFE\) có \(\angle AFB = \angle AEB = {90^0}\) nên là tứ giác nội tiếp (tứ giác có hai đỉnh kề nhau cùng nhìn cạnh đối diện dưới các góc bằng nhau) (đpcm). b) Chứng minh rằng \(A{B^2} = AD.AC\). Ta có:\(d//d'\) \( \Rightarrow \angle {B_1} = \angle {A_1}\) (so le trong) Mà \(\angle {A_1} = \angle {C_1}\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AB\)) \( \Rightarrow \angle {B_1} = \angle {C_1}\,\,\,\left( { = \angle {A_1}} \right)\). Xét \(\Delta ABD\) và \(\Delta ACB\) có: \(\angle A\,\,\,chung\) \(\angle {B_1} = \angle {C_1}\,\,\,\left( {cmt} \right)\) \( \Rightarrow \Delta ABD \sim \Delta ACB\,\,\,\left( {g - g} \right)\) \( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AD}}{{AB}}\) (các cặp cạnh tương ứng tỉ lệ) \( \Rightarrow A{B^2} = AD.AC\) (đpcm). c) Gọi M, N lần lượt là trung điểm của AB, BC. Chứng minh rằng \(MN\) vuông góc với \(EF\). Gọi \(H\) là giao điểm của \(EF\) với \(AC\). Ta có: \(\angle {E_1} = \angle {E_2}\) (đối đỉnh) Tứ giác \(ABFE\) nội tiếp nên \(\angle {E_2} = \angle {A_2}\) (góc nội tiếp cùng chắn cung \(BF\)) \( \Rightarrow \angle {E_1} = \angle {A_2}\) \(\left( { = \angle {E_2}} \right)\) Lại có \(\Delta ABD \sim \Delta ACB\left( {cmt} \right)\) nên \(\angle ADB = \angle ABC\) (góc tương ứng) \( \Rightarrow \angle ADB + \angle {E_1} = \angle ABC + \angle {A_2} = {90^0}\) \( \Rightarrow \angle EHD = {180^0} - \left( {\angle ADB + \angle {E_1}} \right) = {180^0} - {90^0} = {90^0}\) \( \Rightarrow FE \bot AC\) (1) Mà \(MN\) là đường trung bình của \(\Delta ABC\) nên \(MN//AC\) (2) Từ (1) và (2) suy ra \(EF \bot MN\) (đpcm).
|