Đề thi vào 10 môn Toán Hưng Yên năm 2018Tải vềI. PHẦN TRẮC NGHIỆM: Câu 1: Tam giác MNP đều, nội tiếp đường tròn (O; R)
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài I. PHẦN TRẮC NGHIỆM: Câu 1: Tam giác MNP đều, nội tiếp đường tròn (O; R), khi đó số đo \(\widehat {NOP}\) là: A. \({150^0}\) B. \({60^0}\) C. \({30^0}\) D. \({120^0}\) Câu 2: Phương trình nào sau đây có hai nghiệm trái dấu? A. \({x^2} - 2017x - 2018 = 0\) B. \({x^2} - 2018x + 2017 = 0\) C. \( - {x^2} + 2017x - 2018 = 0\) D. \({x^2} - 2019x + 2018 = 0\) Câu 3: Tìm m để hàm số \(y = \dfrac{3}{{m + 2}}x + 1\) đồng biến trên tập số thực \(R.\) A. \(m > - 2\) B. \(m < - 2\) C. \(m > 2\) D. \(m \le - 2\) Câu 4: Biết \(\left( {a;\;b} \right)\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}4x - 3y = 2\\x + y = 4\end{array} \right..\) Khi đó giá trị của biểu thức \(2{a^2} - {b^2}\) là: A. 4 B. -12 C. -4 D. 8 Câu 5: Giá trị của biểu thức \(\sin {62^0} - \cos {28^0}\) bằng: A. 0 B. 1 C. \(2\sin {62^0}\) D. \(2\cos {28^0}\) Câu 6: Hệ số góc của đường thẳng \(y = - 5x + 7\) là: A. \( - 5x\) B. \(5\) C. \( - 5\) D. \(7\) Câu 7: Cho tam giác \(ABC\) vuông tại \(C.\) Biết \(\sin B = \dfrac{1}{3},\) khi đó \(\tan A\) bằng: A. \(\dfrac{{2\sqrt 2 }}{3}\) B. \(3\) C. \(2\sqrt 2 \) D. \(\dfrac{1}{{2\sqrt 2 }}\) Câu 8: Cho hai đường tròn \(\left( {O;\;4cm} \right)\) và đường tròn \(\left( {I;\;2cm} \right),\) biết \(OI = 6cm.\) Số tiếp tuyến chung của hai đường tròn đó là: A. 4 B. 3 C. 2 D. 1 Câu 9: Kết quả của phép tính \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt 5 \) là: A. \(2\sqrt 5 - 2\) B. \( - 2\) C. \(2\) D. \(2 - 2\sqrt 5 \) Câu 10: Tìm m để hai đường thẳng \(\left( d \right):\;\;y = 3x + 1\) và \(\left( {d'} \right):\;\;y = \left( {m - 1} \right)x - 2m\) song song với nhau. A. \(m = - \dfrac{1}{2}\) B. \(m = 4\) C. \(m = - \dfrac{3}{2}\) D. \(m \ne 4\)
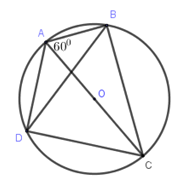
Câu 12: Cho tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AC\), có \(\widehat {BAC} = {60^0}\) (hình vẽ).
Khi đó số đo của \(\widehat {ADB}\) là: A. \({45^0}\) B. \({60^0}\) C. \({40^0}\) D. \({30^0}\). Câu 13: Một hình cầu có đường kính 6cm. Diện tích mặt cầu đó là: A. \(36\pi c{m^2}\) B. \(12\pi c{m^2}\) C. \(216\pi c{m^2}\) D. \(72\pi c{m^2}\) Câu 14: Cặp số nào sau đây là một nghiệm của phương trình \(x - 3y = - 1?\) A. \(\left( {2;\;0} \right)\) B. \(\left( {2;\;1} \right)\) C. \(\left( {1;\;2} \right)\) D. \(\left( {2;\; - 1} \right)\) Câu 15: Trên cùng mặt phẳng tọa độ Oxy cho ba đường thẳng \(y = x + 2;\;y = 2x + 1\) và \(y = \left( {{m^2} - 1} \right)x - 2m + 1.\) Tìm giá trị của m để ba đường thẳng cùng đi qua một điểm. A. \(m = - 3\) B. \(m \in \left\{ { - 3;\;1} \right\}\) C. \(m \in \left\{ { - 1;\;3} \right\}\) D. \(m = 1\) Câu 16: Trong mặt phẳng tọa độ Oxy, tập nghiệm của phương trình \(4x + y = 1\) được biểu diễn bởi đồ thị hàm số nào dưới đây? A. \(y = 4x + 1\) B. \(y = - 4x - 1\) C. \(y = - 4x + 1\) D. \(y = 4x - 1\) Câu 17: Cho \(\Delta ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(BH = 3,2cm;\;\;BC = 5cm\) thì độ dài \(AB\) bằng: A. \(8cm\) B. -\(16cm\) C. \(1,8cm\) D. \(4cm\) Câu 1: Biết phương trình \(3{x^2} + 6x - 9 = 0\) có hai nghiệm \({x_1};{x_2}\). Giả sử \({x_1} < {x_2}\) khi đó biểu thức \(\dfrac{{{x_2}}}{{{x_1}}}\) có giá trị là: A. \(\dfrac{1}{3}\) B. \( - \dfrac{1}{3}\) C. \( - 3\) D. 3 Câu 19: Cho các đường tròn \(\left( {A;3cm} \right);\,\,\left( {B;\;5cm} \right);\,\,\left( {C;2cm} \right)\) đôi một tiếp xúc ngoài với nhau. Chu vi của \(\Delta ABC\) là: A. 20cm B. \(10\sqrt 2 cm\) C. 10cm D. \(10\sqrt 3 cm\) Câu 20: Điều kiện xác định của biểu thức \(\sqrt {x - 15} \) là: A. \(x \le - 15\) B. \(x \ge 15\) C. \(x \ge - 15\) D. \(x \le 15\) Câu 21: Kết quả rút gọn biểu thức \(\dfrac{1}{{\sqrt {13} + \sqrt {15} }} + \dfrac{1}{{\sqrt {15} + \sqrt {17} }}\) là: A. \(\dfrac{{\sqrt {13} - \sqrt {17} }}{2}\) B. \(\dfrac{{\sqrt {17} + \sqrt {13} }}{2}\) C. \(\sqrt {17} - \sqrt {13} \) D. \(\dfrac{{\sqrt {17} - \sqrt {13} }}{2}\) Câu 22: Đổ nước vào một chiếc thùng hình trụ có bán kính 20cm. Nghiêng thùng sao cho mặt nước chạm miệng thùng và đáy thùng (như hình vẽ) thì mặt nước tạo với đáy thùng một góc 450. Thể tích của thùng là: A. \(400\pi \,\,\left( {c{m^3}} \right)\) B. \(32000\pi \,\left( {c{m^3}} \right)\) C. \(16000\pi \,\left( {c{m^3}} \right)\) D. \(8000\pi \,\left( {c{m^3}} \right)\) Câu 23: Cho hai đường thẳng \(\left( {{d_1}} \right):\,\,y = - 2x + 3\) và \(\left( {{d_2}} \right):\,\,y = - \dfrac{1}{2}x + 3\). Khẳng định nào sau đây là đúng? A. (d1) và (d2) trùng nhau B. (d1) và (d2) cắt nhau tại một điểm trên trục trung C. (d1) và (d2) song song với nhau D. (d1) và (d2) cắt nhau tại một điểm trên trục hoành. Câu 24: Số nhà của bạn Nam là một số tự nhiên có hai chữ số. Nếu thêm chữ số 7 vào bên trái số đó thì được một số kí hiệu là A. Nếu thêm chữ số 7 vào bên phải chữ số đó thì được một số kí hiệu là B. Tìm số nhà của bạn Nam biết \(A - B = 252\). A. 45 B. 54 C. 90 D. 49 Câu 25: Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right):\,\,y = x - m + 2\) và parabol: \(\left( P \right):\,\,y = {x^2}\). Tìm m để (d) và (P) cắt nhau tại hai điểm phân biệt nằm trên cùng một nửa mặt phẳng có bờ là trục tung: A. \(m > \dfrac{9}{4}\) B. \(\dfrac{4}{9} < m < 2\) C. \(2 < m < \dfrac{9}{4}\) D. \(m < \dfrac{4}{9}\) II. PHẦN TỰ LUẬN: 45 PHÚT Câu 1 (1,5 điểm). a) Rút gọn biểu thức \(P = \sqrt 3 \left( {\sqrt {12} - 3} \right) + \sqrt {27} \) b) Tìm giá trị của m để đồ thị hàm số \(y = m{x^2}\) đi qua điểm \(A\left( {2;4} \right)\). c) Giải phương trình \({x^2} - 6x + 5 = 0\) Câu 2 (1,5 điểm). Cho hệ phương trình \(\left\{ \begin{array}{l}3x - y = 2m + 3\\x + 2y = 3m + 1\end{array} \right.\) (m là tham số) a) Giải hệ phương trình khi \(m = 2\). b) Tìm m để hệ phương trình có nghiệm \(\left( {x;y} \right)\) thỏa mãn điều kiện \({x^2} + {y^2} = 5\). Câu 3 (1,5 điểm) Cho đường tròn (O) đường kính AB và một dây CD vuông góc với AB tại H (H không trừng với các điểm A, B, O). Gọi M là trung điểm của AD. Chứng minh: a) Bốn điểm O, M, D, H cùng thuộc một đường tròn. b) MH vuông góc với BC. Câu 4 (0,5 điểm) Cho x, y, z là 3 số thực dương thỏa mãn \({x^2} + {y^2} + {z^2} = 2\). Tìm giá trị lớn nhất của biểu thức \(A = \dfrac{2}{{{x^2} + {y^2}}} + \dfrac{2}{{{y^2} + {z^2}}} + \dfrac{2}{{{z^2} + {x^2}}} - \dfrac{{{x^3} + {y^3} + {z^3}}}{{2xyz}}\) Lời giải I. PHẦN TRẮC NGHIỆM:
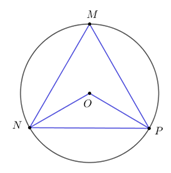
Câu 1: Phương pháp: Số đo góc nội tiếp bằng nửa số đo góc ở tâm cùng chắn một cung. Cách giải: Tam giác \(MNP\) là tam giác đều \( \Rightarrow \widehat M = \widehat N = \widehat P = {60^0}.\) Xét đường tròn \(\left( {O;\;R} \right)\) ta có: \(\widehat {NMP}\) là góc nội tiếp chắn cung \(NP.\) \(\widehat {NOP}\) là góc ở tâm chắn cung \(NP.\) \( \Rightarrow \widehat {NOP} = 2.\widehat {NMP} = {2.60^0} = {120^0}.\) Chọn D. Câu 2: Phương pháp: Phương trình bậc hai một ẩn có hai nghiệm trái dấu \( \Leftrightarrow ac < 0.\) Cách giải: +) Phương trình \({x^2} - 2017x - 2018 = 0\) có \(ac = 1.\left( { - 2018} \right) = - 2018 < 0 \Rightarrow \) phương trình có hai nghiệm trái dấu. Chọn A. Câu 3: Phương pháp: Hàm số \(y = ax + b\) đồng biến \( \Leftrightarrow a > 0.\) Cách giải: Hàm số đồng biến trên \(R \Leftrightarrow \dfrac{3}{{m + 2}} > 0 \Leftrightarrow m + 2 > 0\;\;\left( {do\;\;3 > 0} \right) \Leftrightarrow m > - 2.\) Chọn A. Câu 4: Phương pháp: Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số. Cách giải: Ta có: \(\left\{ \begin{array}{l}4x - 3y = 2\\x + y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - 3y = 2\\3x + 3y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7x = 14\\y = 4 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right..\) \( \Rightarrow \) Hệ phương trình có nghiệm \(\left( {x;\;y} \right) = \left( {a;\;b} \right) = \left( {2;\;2} \right)\) hay \(a = 2,\;\;b = 2.\) \( \Rightarrow 2{a^2} - {b^2} = {2.2^2} - {2^2} = 4.\) Chọn A. Câu 5: Phương pháp: Sử dụng công thức: \(\cos \alpha = sin\left( {{{90}^0} - \alpha } \right).\) Cách giải: Ta có: \({28^0} = {90^0} - {62^0} \Rightarrow \cos {28^0} = \sin {62^0}.\) \( \Rightarrow \sin {62^0} - \cos {28^0} = \sin {62^0} - \sin {62^0} = 0.\) Chọn A. Câu 6: Phương pháp: Đường thẳng \(y = ax + b\;\;\left( {a \ne 0} \right)\) có hệ số góc là \(a.\) Cách giải: Hệ số góc của đường thẳng \(y = - 5x + 7\) là: \(a = - 5.\) Chọn C. Câu 7: Phương pháp: Sử dụng hệ thức lượng của góc nhọn trong tam giác vuông và định lý Pi-ta-go. Cách giải :
Xét tam giác \(ABC\) vuông tại \(C\) ta có: \(\sin B = \dfrac{{AC}}{{AB}} = \dfrac{1}{3} \Rightarrow AB = 3AC.\) Mà áp dụng định lý Pi-ta-go ta có: \(A{B^2} = A{C^2} + B{C^2} \Leftrightarrow {\left( {3AC} \right)^2} = A{C^2} + B{C^2}\) \( \Leftrightarrow 8A{C^2} = B{C^2} \Leftrightarrow \dfrac{{B{C^2}}}{{A{C^2}}} = 8 \Leftrightarrow \dfrac{{BC}}{{AC}} = 2\sqrt 2 = \tan A.\) Chọn C. Câu 8: Phương pháp: Áp dụng kiến thức về vị trí tương đối của hai đường tròn. Cách giải:
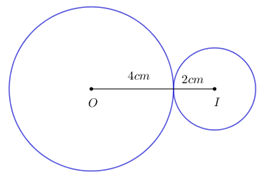
Ta có: \(OI = 6cm = 4 + 2 = R + r.\) \( \Rightarrow \left( {O;\;4cm} \right)\) tiếp xúc ngoài với \(\left( {I;\;2cm} \right).\) \( \Rightarrow \) Hai đường tròn này có 3 đường tiếp tuyến chung. Chọn B. Câu 9: Phương pháp: Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \;\;khi\;\;\;A \ge 0\\ - A\sqrt B \;\;khi\;\;A < 0\end{array} \right..\) Cách giải: \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt 5 = \left| {2 - \sqrt 5 } \right| - \sqrt 5 = \sqrt 5 - 2 - \sqrt 5 = - 2.\;\;\;\left( {do\;\;2 - \sqrt 5 < 0} \right).\) Chọn B. Câu 10: Phương pháp: Hai đường thẳng \({d_1}:\;y = {a_1}x + {b_1},\;\;{d_2}:\;\;y = {a_2}x + {b_2}.\) Hai đường thẳng \({d_1}//{d_2} \Leftrightarrow \left\{ \begin{array}{l}{a_1} = {a_2}\\{b_1} \ne {b_2}\end{array} \right..\) Cách giải: Ta có:\(d//d' \Leftrightarrow \left\{ \begin{array}{l}m - 1 = 3\\1 \ne - 2m\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 4\\m \ne - \dfrac{1}{2}\end{array} \right. \Leftrightarrow m = 4.\) Chọn B. Câu 11: Phương pháp: Áp dụng định lý Pi-ta-go và bất đẳng thức Cô-si để làm bài toán. Cách giải:
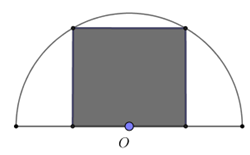
Gọi kích thước của miếng tôn như hình vẽ. Áp dụng định lý Pi-ta-go ta có: \({a^2} + {\left( {\dfrac{b}{2}} \right)^2} = 1 \Leftrightarrow {a^2} = \dfrac{{4 - {b^2}}}{4} \Leftrightarrow a = \dfrac{{\sqrt {4 - {b^2}} }}{2}.\) Khi đó diện tích miếng tôn hình chữ nhật là: \(S = ab = \dfrac{{b\sqrt {4 - {b^2}} }}{2}.\)
Áp dụng bất đẳng thức Cô-si cho hai số ta có: \({b^2} + \sqrt {{{\left( {4 - {b^2}} \right)}^2}} \ge 2b\sqrt {4 - {b^2}} \Leftrightarrow b\sqrt {4 - {b^2}} \le \dfrac{{{b^2} + 4 - {b^2}}}{2} = 2.\) \( \Rightarrow S = \dfrac{{b\sqrt {4 - {b^2}} }}{2} \le \dfrac{2}{2} = 1.\) Dấu “=” xảy ra \( \Leftrightarrow b = \sqrt {4 - {b^2}} \Leftrightarrow {b^2} = 4 - {b^2} \Leftrightarrow {b^2} = 2 \Leftrightarrow b = \sqrt 2 .\) Vậy diện tích lớn nhất có thể là \(1{m^2}.\) Chọn C. Câu 12: Phương pháp: Tính \(\widehat {ADC},\widehat {BDC}\) Cách giải: Ta có: \(\widehat {ADC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn). \(\widehat {BDC} = \widehat {BAC} = {60^0}\) (góc nội tiếp cùng chắn cung \(BC\)). Do đó \(\widehat {ADB} = \widehat {ADC} - \widehat {BDC} = {90^0} - {60^0} = {30^0}\). Chọn D. Câu 13: Phương pháp: Công thức tính diện tích mặt cầu bán kính \(r:\;\;S = 4\pi {r^2}.\) Cách giải: Ta có diện tích mặt cầu đó là: \(S = 4\pi .{\left( {\dfrac{6}{2}} \right)^2} = 36\pi c{m^2}.\) Chọn A. Câu 14: Phương pháp: Thay các cặp số của từng đáp án vào phương trình. Cặp số nào không thỏa mãn phương trình là đáp án cần chọn. Cách giải: Thay \(\left( {2;\;0} \right)\) vào phương trình ta được: \(2 - 3.0 = 2 \ne - 1 \Rightarrow \left( {2;\;0} \right)\) không là nghiệm của phương trình. Thay \(\left( {2;1} \right)\) vào phương trình ta được \(2 - 3.1 = 2 - 3 = - 1 \Rightarrow \left( {2;1} \right)\) là nghiệm của phương trình. Chọn B. Câu 15: Phương pháp: Tìm giao điểm của hai đường thẳng đã biết phương trình bằng cách giải hệ phương trình. Sau đó thế tọa độ giao điểm đã tìm được vào phương trình đường thẳng chứa tham số m để tìm m. Cách giải: Tọa độ giao điểm của hai đường thẳng \(y = x + 2;\;y = 2x + 1\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}y = x + 2\\y = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = x + 2\\x + 2 = 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 3\end{array} \right. \Rightarrow A\left( {1;\;3} \right).\) Để bai đường thẳng đã cho cùng đi qua một điểm thì đường thẳng \(y = \left( {{m^2} - 1} \right)x - 2m + 1\) phải đi qua điểm \(A\left( {1;\;\;3} \rig
|