Đề thi vào 10 môn Toán Huế năm 2023

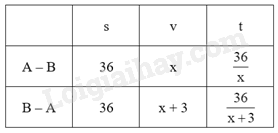
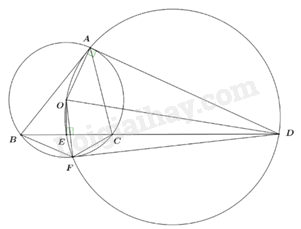
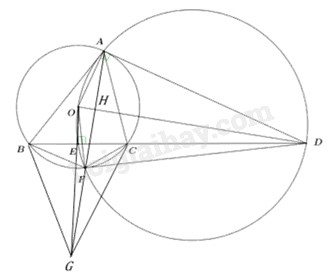
Đề bài

Câu 1: (1,5 điểm)

a) Tìm điều kiện của x để biểu thức \(A = \sqrt {x - 1} \) có nghĩa.

b) Không sử dụng máy tính cầm tay, tính giá trị của biểu thức \(B = \sqrt 9 {\rm{ \;}} - \sqrt 4 {\rm{ \;}} + \sqrt {16} \).

Câu 2: (1,5 điểm)

a) Không sử dụng máy tính cầm tay, giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - y = 1}\end{array}} \right.\)

b) Trên mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right):y = x - m\).Tìm tất cả các giá trị của m để đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ bằng 2.

Câu 3: (1 điểm) Một người đi xe đạp với vận tốc không đổi từ A đến B cách nhau 36km. Trên cùng tuyến đường đó, khi đi từ B trở về A, người này đi với vận tốc lớn hơn 3km/h so với vận tốc khi đi từ A đến B vì vậy thời gian về ít hơn thời gian đi là 36 phút. Tính vận tốc của người đi xe đạp khi đi từ A đến B.

Câu 4: (2 điểm) Cho phương trình \({x^2} - 2\left( {m + 3} \right)x + 2m + 1 = 0\) \((1)\)(với x là ẩn số)

a) Giải phương trình (1) khi m = -2.

b) Chứng minh phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị của m.

c) Tìm tất cả các giá trị của m để phương trình (1) có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn:

\({x_1}^2 + {x_2}^2 - 2{x_1} - 2{x_2} = 10\)

Câu 5: (3 điểm) Cho tam giác ABC có ba góc nhọn, AB > AC và nội tiếp đường tròn (O). Tiếp tuyến của đường tròn (O) tại A cắt đường thẳng BC tại D. Gọi E là hình chiếu vuông góc của O trên đường thẳng BC.

a) Chứng minh AOED là tứ giác nội tiếp.

b) Đường tròn ngoại tiếp tứ giác AEOD cắt đường tròn (O) tại điểm thứ hai là F (F không trùng với A). Chứng minh DF là tiếp tuyến của đường tròn (O) và \(\frac{{AB}}{{AC}} = \frac{{FB}}{{FC}}\).

c) Các tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại G. Chứng minh ba điểm A, F, G thẳng hàng.

Câu 6: (1 điểm) Cho tam giác OBC vuông tại O. Nếu quay tam giác OBC một vòng quanh cạnh OB thì được một hình nón có thể tích bằng \(800\pi {\mkern 1mu} c{m^3}\). Nếu quay tam giác OBC một vòng quanh cạnh OC cố định thì được một hình nón có thể tích bằng \(1920\pi {\mkern 1mu} c{m^3}\). Tính OB và OC.

-----HẾT-----

Lời giải chi tiết

Câu 1 (NB):

Phương pháp:

a) Điều kiện xác định của \(\sqrt {f(x)} \) là \(f(x) \ge 0\)

b) Thực hiện tính toán với tính chất \(\sqrt {{x^2}} {\rm{ \;}} = \left| x \right|\)

Cách giải:

a) Biểu thức \(A = \sqrt {x - 1} \) có nghĩa khi \(x - 1 \ge 0 \Leftrightarrow x \ge 1\).

Vậy biểu thức A có nghĩa khi \(x \ge 1\).

b) Ta có:

\(\begin{array}{*{20}{l}}{B = \sqrt 9 {\rm{ \;}} - \sqrt 4 {\rm{ \;}} + \sqrt {16} }\\{B = \sqrt {{3^2}} {\rm{ \;}} - \sqrt {{2^2}} {\rm{ \;}} + \sqrt {{4^2}} }\\{B = 3 - 2 + 4}\\{B = 5}\end{array}\).

Vậy B = 5.

Câu 2 (TH):

Phương pháp:

a) Giải hệ phương trình bằng phương pháp cộng đại số.

b) Đường thẳng \(y = ax + b(a \ne 0)\) cắt trục tung tại điểm có tọa độ \((0;b)\)

Cách giải:

a) \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 5}\\{x - y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x = 6}\\{y = x - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = x - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 1}\end{array}} \right.\).

Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {2;1} \right)\).

b) Vì đường thẳng \(\left( d \right)\) cắt trục tung tại điểm có tung độ bằng 2 nên đường thẳng (d) đi qua điểm (0;2)

Thay x = 0, y = 2 vào phương trình đường thẳng (d) ta được: \(2 = 0 - m \Leftrightarrow m = {\rm{ \;}} - 2\).

Vậy \(m = {\rm{ \;}} - 2.\)

Câu 3 (TH):

Phương pháp:

Giải bài toán bằng cách lập phương trình.

Thời gian lúc đi nhiều hơn thời gian lúc về 36 phút = \(\frac{3}{5}\) giờ

Cách giải:

Đổi 36 phút = \(\frac{3}{5}\) giờ.

Gọi vận tốc của người đi xe đạp khi đi từ A đến B là x (km/h) (x > 0)

Vận tốc của người đi xe đạp khi đi từ B trở về A là x + 3 (km/h)

Thời gian người đi xe đạp đi từ A đến B là: \(\frac{{36}}{x}\)(h)

Thời gian người đi xe đạp đi từ B trở về A là: \(\frac{{36}}{{x + 3}}\)(h)

Vì thời gian về ít hơn thời gian đi là 36 phút = \(\frac{3}{5}\) giờ nên ta có phương trình:

\(\begin{array}{l}\frac{{36}}{x} - \frac{{36}}{{x + 3}} = \frac{3}{5}\\ \Leftrightarrow \frac{{180\left( {x + 3} \right)}}{{5x\left( {x + 3} \right)}} - \frac{{180x}}{{5x\left( {x + 3} \right)}} = \frac{{3x\left( {x + 3} \right)}}{{5x\left( {x + 3} \right)}}\\ \Rightarrow 180\left( {x + 3} \right) - 180x = 3x\left( {x + 3} \right)\\ \Leftrightarrow 180x + 540 - 180x = 3{x^2} + 9x\\ \Leftrightarrow 3{x^2} + 9x - 540 = 0\\ \Leftrightarrow {x^3} + 3x - 180 = 0\\ \Leftrightarrow {x^2} - 12x + 15x - 180 = 0\\ \Leftrightarrow x\left( {x - 12} \right) + 15\left( {x - 12} \right) = 0\\ \Leftrightarrow \left( {x - 12} \right)\left( {x + 15} \right) = 0\\ \Leftrightarrow \left\{ \begin{array}{l}x = 12\,\,\,\left( {tm} \right)\\x =  - 15\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)

Vậy vận tốc của người đi xe đạp khi đi từ A đến B là 12 km/h.

Câu 4 (TH):

Phương pháp:

a) Thay m = -2 vào phương trình.

Giải phương trình bậc hai một ẩn bằng phương pháp nhẩm nghiệm: a – b + c = 0 thì PT có một nghiệm là -1, nghiệm còn lại là \(\frac{{ - c}}{a}\)

b) Công thức \(\Delta ' = {\left( {\frac{b}{a}} \right)^2} - a.c\). Chứng minh \(\Delta {\rm{ \;}} > 0\) với mọi m.

c) Hệ thức vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)

Biến đổi theo yêu cầu đề bài cho.

Cách giải:

a) Thay m = -2 vào phương trình (1) ta có: \({x^2} - 2\left( { - 2 + 3} \right)x + 2.( - 2) + 1 = 0\) \( \Leftrightarrow {x^2} - 2x - 3 = 0\).

Ta có \(a - b + c = 1 - \left( { - 2} \right) + \left( { - 3} \right) = 0\) nên phương trình có 2 nghiệm phân biệt \(\left[ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 1}\\{x = \frac{{ - c}}{a} = 3}\end{array}} \right.\).

Vậy khi m = -2 thì tập nghiệm của phương trình là \(S = \left\{ { - 1;3} \right\}\).

b) Ta có:

\(\begin{array}{*{20}{l}}{\Delta ' = {{\left[ { - \left( {m + 3} \right)} \right]}^2} - 2m - 1}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}  = {m^2} + 6m + 9 - 2m - 1}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}  = {m^2} + 4m + 8}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu}  = {{\left( {m + 2} \right)}^2} + 4 \ge 4,\forall m}\end{array}\)

\( \Rightarrow \Delta ' > 0,\forall m\).

Vậy phương trình (1) luôn có 2 nghiệm phân biệt với mọi giá trị của m.

c) Theo định lí Vi-ét ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2(m + 3)}\\{{x_1}.{x_2} = 2m + 1}\end{array}} \right.\)

Theo bài ra ta có: \({x_1}^2 + {x_2}^2 - 2{x_1} - 2{x_2} = 10\)

\(\begin{array}{l} \Leftrightarrow \left( {{x_1}^2 + {x_2}^2} \right) - 2({x_1} + {x_2}) = 10\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 2({x_1} + {x_2}) = 10\\ \Leftrightarrow {\left[ {2(m + 3)} \right]^2} - 2.(2m + 1) - 2.2(m + 3) = 10\\ \Leftrightarrow 4\left( {{m^2} + 6m + 9} \right) - 4m - 2 - 4m - 12 = 10\\ \Leftrightarrow 4{m^2} + 16m + 12 = 0\\ \Leftrightarrow {m^2} + 4m + 3 = 0\\ \Leftrightarrow {m^2} + m + 3m + 3 = 0\\ \Leftrightarrow m\left( {m + 1} \right) + 3\left( {m + 1} \right) = 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {m + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m =  - 1\\m =  - 3\end{array} \right.\,\,\,\left( {tm} \right)\end{array}\)

Vậy \(m = {\rm{ \;}} - 3\) hoặc \(m = {\rm{ \;}} - 1\) là giá trị cần tìm.

Câu 5 (VD):

Phương pháp:

a) Chứng minh tứ giác có hai góc có tổng bằng \({180^0}\)

b) Chứng minh OD là đường kính của đường tròn ngoại tiếp tứ giác AEOD

Mà F thuộc đường tròn ngoại tiếp tứ giác AEOD \( \Rightarrow DF \bot OF\)tại F

Mà OF là bán kính của (O) nên DF là tiếp tuyến của (O)

c) Chứng minh $\Delta DCF\backsim \Delta DFB\left( g.g \right)\Rightarrow \frac{FB}{FC}=\frac{DB}{DF}$

Chứng minh $\Delta DAC\backsim \Delta DBA\left( g.g \right)$$\Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{DB}}{{DA}}$

Mà \(DA = DF\)  (tính chất 2 tiếp tuyến cắt nhau)

Suy ra dpcm.

c) Gọi H là giao điểm của AF và OD. Chứng minh \(A{O^2} = OH.OD\)

Chứng minh O, E, G thẳng hàng. Chứng mimh \(O{C^2} = OE.OG\)

Từ đó chứng minh $\Delta OHG\backsim ~\Delta OED\left( c.g.c \right)$\( \Rightarrow GH \bot OD\)

Mà \(AH \bot OD\) (chứng minh trên)

\( \Rightarrow H,F,G,A\) thẳng hàng

Cách giải:

a) Vì AD là tiếp tuyến của đường tròn (O) tại A nên:

 \(OA \bot AD \Rightarrow \angle OAD = {90^0}\).

Vì E là hình chiếu vuông góc của O trên BC

\( \Rightarrow \angle OED = {90^0}\).

Xét tứ giác AODE có: \(\angle OAD + \angle OED = {90^0} + {90^0} = {180^0}\).

\( \Rightarrow AODE\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).

b)  Xét đường tròn ngoại tiếp tứ giác AEOD có \(\angle OAD = {90^0}\)

\( \Rightarrow \angle OAD\) nội tiếp chắn nửa đường tròn.

=> OD là đường kính của đường tròn ngoại tiếp tứ giác AEOD.

\( \Rightarrow \angle OFD = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow DF \bot OF\) tại F, với OF là một bán kính của (O).

Vậy DF là tiếp tuyến của (O) tại F.

Xét \(\Delta DCF\) và \(\Delta DFB\) có:

\(\angle FDB\) chung

\(\angle DFC = \angle DBF\) (tính chất góc tạo bởi tiếp tuyến và dây cung của (O))

$\Rightarrow \Delta DCF\backsim \Delta DFB\left( g.g \right)\Rightarrow \frac{FB}{FC}=\frac{DB}{DF}$   (1)

Tương tự ta chứng minh $\Delta DAC\backsim \Delta DBA\left( g.g \right)$ (do \(\angle ADB\) chung và \(\angle DAC = \angle DBA\))

\( \Rightarrow \frac{{AB}}{{AC}} = \frac{{DB}}{{DA}}\)        (2)

Mà \(DA = DF\)  (tính chất 2 tiếp tuyến cắt nhau) (3)

Từ (1), (2), (3) suy ra \(\frac{{AB}}{{AC}} = \frac{{FB}}{{FC}}\) (đpcm)

c) Do G là giao điểm của 2 tiếp tuyến tại B, C của (O) nên GB = GC (tính chất)

Mà OB = OC (bán kính) nên OG là trung trực của BC (tính chất)

Mà \(OE \bot BC\) (cmt) nên O, E, G thẳng hàng.

\( \Rightarrow \Delta OCG\) vuông tại C, đường cao CE nên \(O{C^2} = OE.OG\)

Gọi H là giao điểm của AF và OD

Do DA = DF (cmt) và OA = OF (bán kính) nên OD là trung trực của AF (tính chất)

\( \Rightarrow OD \bot AF\) tại H

\( \Rightarrow \Delta AOD\) vuông tại A, đường cao AH nên \(A{O^2} = OH.OD\)

Mà OA = OC (bằng bán kính) nên từ \(OE.OG = OH.OD\)\( \Rightarrow \frac{{OE}}{{OD}} = \frac{{OH}}{{OG}}\)

Mà \(\angle GOD\) chung nên suy ra \(\Delta OHG\backsim ~\Delta OED\left( c.g.c \right)\Rightarrow \angle OHG=\angle DHG={{90}^{0}}\)

\( \Rightarrow GH \bot OD\)

Mà \(AH \bot OD\) (chứng minh trên)

\( \Rightarrow H,F,G,A\) thẳng hàng

Vậy A, F, G thẳng hàng (đpcm)

Câu 6 (VD):

Phương pháp:

Khi quay tam giác OBC một vòng quanh cạnh OB ta được khối nón có bán kính đáy bằng OC, chiều cao bằng OB.

Khi quay tam giác OBC một vòng quanh cạnh OC ta được khối nón có bán kính đáy bằng OB, chiều cao bằng OC.

Cách giải:

Khi quay tam giác OBC một vòng quanh cạnh OB ta được khối nón có bán kính đáy bằng OC, chiều cao bằng OB.

Thể tích hình nón tạo thành khi quay tam giác OBC quanh cạnh OB là: \(\frac{1}{3}\pi .O{C^2}.OB = 800\pi \)

\( \Rightarrow OB.O{C^2} = 2400 \Rightarrow OB = \frac{{2400}}{{O{C^2}}}\)

Khi quay tam giác OBC một vòng quanh cạnh OC ta được khối nón có bán kính đáy bằng OB, chiều cao bằng OC.

Thể tích hình nón tạo thành khi quay tam giác OBC quanh cạnh OC là: \(\frac{1}{3}\pi .O{B^2}.OC = 1920\pi \)

\(\begin{array}{*{20}{l}}{ \Rightarrow O{B^2}.OC = 5760}\\{ \Rightarrow {{\left( {\frac{{2400}}{{O{C^2}}}} \right)}^2}.OC = 5760}\\{ \Rightarrow \frac{{{{2400}^2}}}{{O{C^3}}} = 5760}\\{ \Rightarrow O{C^3} = 1000}\\{ \Rightarrow OC = 10}\\{ \Rightarrow OB = \frac{{2400}}{{O{C^2}}} = \frac{{2400}}{{{{10}^2}}} = 24}\end{array}\)

Vậy \(OB = 24cm;{\mkern 1mu} {\mkern 1mu} OC = 10cm.\)