Đề thi vào 10 môn Toán Hòa Bình năm 2023Tải vềCâu 1: 1. Tìm điều kiện của \(x\) để biểu thức \(\sqrt {x - 2} \) có nghĩa. 2. Tính giá trị của biểu thức: \(A = \sqrt {36} {\rm{ \;}} + \sqrt 9 \)
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
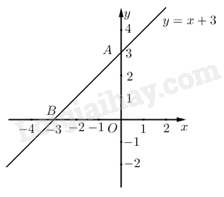
Đề bài Câu 1: 1. Tìm điều kiện của \(x\) để biểu thức \(\sqrt {x - 2} \) có nghĩa. 2. Tính giá trị của biểu thức: \(A = \sqrt {36} {\rm{ \;}} + \sqrt 9 \) 3. Giải các phương trình: \({\rm{a}}) 2x + 1 = 5\) \({\rm{b}}) {x^2} + 2x - 3 = 0\) 4. Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right):y = x + 3.\) a) Vẽ đường thẳng (d). b) Tìm giá trị của m để đường thẳng \(\left( {d'} \right):y = 2x + m - 1\) cắt đường thẳng \(\left( d \right)\) tại một điểm trên trục tung. Câu 2: 1. Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 3}\\{x - 2y = {\rm{ \;}} - 1}\end{array}} \right.\) 2. Cho tam giác ABC vuông tại A, đường cao \(AH\left( {H \in BC} \right)\), biết \(BH = 4cm\), \(HC = 9\;{\rm{cm}}\). Tính độ dài đoạn thẳng AH. Câu 3: 1. Cho phương trình: \({x^2} - 8x + m - 1 = 0\) (m là tham số). Tìm giá trị của m để phương trình có hai nghiệm \({x_1},{x_2}\) sao cho biểu thức \(P = \left( {x_1^2 - 1} \right)\left( {x_2^2 - 1} \right) + 2087\) đạt giá trị nhỏ nhất. 2. Một đội xe dự định chở 120 tấn xi măng vào công trường. Khi chuẩn bị khởi hành thì đội xe được bổ sung thêm 5 chiếc xe nữa, nên cả đội đã chở thêm được 5 tấn và mỗi xe chở ít hơn so với dự định là 1 tấn xi măng. Hỏi theo dự định đội xe có bao nhiêu chiếc xe? Biết khối lượng xi măng mỗi xe chở là như nhau và mỗi xe chỉ chở đúng một chuyến. Câu 4: Cho đường tròn (O;R) có đường kính AB . Lấy điểm I bất kỳ thuộc đoạn thẳng AB (I khác A và B). Qua I kẻ một đường thẳng d bất kỳ cắt đường tròn (O) tại M và N sao cho AM < AN (M khác A và B; N khác A và B). Từ A kẻ AP vuông góc với MN tại P, từ I kẻ IQ vuông góc với AN tại Q. Chứng minh rằng: a) Tứ giác APIQ là tứ giác nội tiếp. b) PM.AI = MA.QI. c) \(AM.BN + AN.BM \le 4{R^2}\) Câu 5: 1. Tìm nghiệm nguyên của phương trình: \(2{x^2} + 3xy + {y^2} + 5x + 3y = 11\) 2. Cho a, b là các số thực thỏa mãn \(4{a^2} - 2ab + {b^2} = 4a + 2b\). Tìm giá trị lớn nhất của biểu thức \(P = 253(2a + b)\). -----HẾT----- Lời giải chi tiết Câu 1 (VD): Phương pháp: 1. \(\sqrt {\rm{A}} \) có nghĩa khi \(A \ge 0\). 2. Căn bậc hai của một số \(a\) là một số \(x\) sao cho \({x^2} = a\) Cách giải: 1. Tìm điều kiện của \(x\) để biểu thức \(\sqrt {x - 2} \) có nghĩa. Biểu thức \(\sqrt {x - 2} \) có nghĩa khi và chỉ khi \(x - 2 \ge 0 \Leftrightarrow x \ge 2\) Vậy với \(x \ge 2\) thì biểu thức đã cho có nghĩa. 2. Tính giá trị của biểu thức: \(A = \sqrt {36} + \sqrt 9 \) Ta có: \(A = \sqrt {36} + \sqrt 9 = \sqrt {{6^2}} + \sqrt {{3^2}} = 6 + 3 = 9\) Vậy \(A = 9.\) 3. Giải các phương trình: \(\begin{array}{l}{\rm{a}})\,\,2x + 1 = 5\\ \Leftrightarrow 2x\,\,\,\,\,\,\,\, = 5 - 1\\ \Leftrightarrow 2x\,\,\,\,\,\,\,\, = 4\\ \Leftrightarrow \,\,\,\,x\,\,\,\,\,\,\,\, = 2\end{array}\) Vậy phương trình đã cho có nghiệm duy nhất là: \(x = 2.\) \({\rm{b}})\,\,{x^2} + 2x - 3 = 0\) Do \(a + b + c = 1 + 2 - 3 = 0\) nên phương trình có 2 nghiệm phân biệt \(\,\left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\) Vậy phương trình đã cho có 2 nghiệm là: \(x = 1\) hoặc \(x = - 3.\) 4. Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right):y = x + 3.\) a) Vẽ đường thẳng (d). Cho \(x = 0 \Rightarrow y = 3\) \(y = 0 \Rightarrow 0 = x + 3 \Leftrightarrow x = - 3\) Vẽ đường thẳng đi qua 2 điểm \(A\left( {0;3} \right)\) và \(B\left( { - 3;0} \right)\) ta được đồ thị hàm số \(y = x + 3\) như sau:
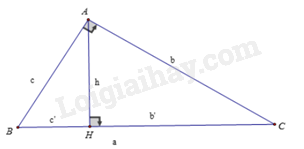
b) Tìm giá trị của m để đường thẳng \(\left( {d'} \right):y = 2x + m - 1\) cắt đường thẳng \(\left( d \right)\) tại một điểm trên trục tung. Đường thẳng \(\left( {d'} \right):y = 2x + m - 1\) cắt đường thẳng \(\left( d \right)\) tại một điểm trên trục tung nên thay x = 0 vào (d) ta được \(y = 0 + 3 \Leftrightarrow y = 3\) Vậy (d) cắt (d’) tại điểm (0,3). Thay \(x = 0,y = 3\) vào (d’) ta được \(\begin{array}{l}3 = 2.0 + m - 1\\ \Leftrightarrow m = 4\end{array}\) Vậy \(m = 4.\) Câu 2 (VD): Phương pháp: 1. Sử dụng phương pháp thế hoặc trừ vế. 2. Tam giác ABC vuông tại A, AH là đường cao, ta có: \({\rm{A}}{{\rm{H}}^2} = {\rm{CH}} \cdot {\rm{BH}}\) hay \({{\rm{h}}^2} = {\rm{b}}' \cdot {\rm{c}}'\)
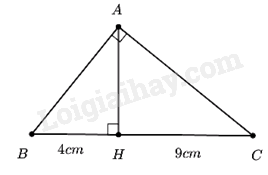
Cách giải: 1. Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 3}\\{x - 2y = - 1}\end{array}} \right.\) \(\left\{ {\begin{array}{*{20}{l}}{2x + y = 3}\\{x - 2y = - 1}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + y = 3\\2x - 4y = - 2\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{5y = 5}\\{x = - 1 + 2y}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 1}\\{x = - 1 + 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 1}\\{x = 1}\end{array}} \right.\). Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {1;1} \right)\). 2. Cho tam giác ABC vuông tại A, đường cao \(AH\left( {H \in BC} \right)\), biết \(BH = 4cm\), \(HC = 9\;{\rm{cm}}\). Tính độ dài đoạn thẳng AH.
Áp dụng hệ thức lượng trong tam giác vuông ABC có: \(\begin{array}{l}A{H^2} = HB.HC = 9.4 = 36\\ \Rightarrow AH = \sqrt {36} = 6cm\end{array}\) Vậy đoạn AH = 6cm. Câu 3 (VD): Phương pháp: 1. Sử dụng vi et: Nếu phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) có 2 nghiệm \({x_1},{x_2}\) thì \(\left\{ {\begin{array}{*{20}{l}}{S = {X_1} + {X_2} = \frac{{ - b}}{a}}\\{P = {x_1} \cdot {X_2} = \frac{c}{a}}\end{array}} \right.\) 2. Giải bài toán bằng cách lập phương trình. Cách giải: 1. Cho phương trình: \({x^2} - 8x + m - 1 = 0\) (m là tham số). Tìm giá trị của m để phương trình có hai nghiệm \({x_1},{x_2}\) sao cho biểu thức \(P = \left( {x_1^2 - 1} \right)\left( {x_2^2 - 1} \right) + 2087\) đạt giá trị nhỏ nhất. Xét \(\Delta ' = {\left( { - 4} \right)^2} - 1\left( {m - 1} \right) = 16 - m + 1 = 17 - m\) Để phương trình có hai nghiệm \({x_1},{x_2}\) thì \(\Delta ' \ge 0 \Leftrightarrow 17 - m \ge 0 \Leftrightarrow m \le 17\) Khi đó áp dụng Viet ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 8\\{x_1}{x_2} = m - 1\end{array} \right.\) Ta có \(P = \left( {x_1^2 - 1} \right)\left( {x_2^2 - 1} \right) + 2087\) \(\begin{array}{l} = x_1^2x_2^2 - \left( {x_1^2 + x_2^2} \right) + 1 + 2087\\ = {\left( {{x_1}{x_2}} \right)^2} - \left[ {{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2}} \right] + 2088\end{array}\) \( = {\left( {m - 1} \right)^2} - {8^2} + 2\left( {m - 1} \right) + 2088\) \( = {\left( {m - 1} \right)^2} + 2\left( {m - 1} \right) + 1 + 2023\) \(\begin{array}{l} = {\left( {m - 1 + 1} \right)^2} + 2023\\ = {m^2} + 2023\end{array}\) Do \({m^2} \ge 0\forall m\) \( \Rightarrow P \ge 2023\) \( \Rightarrow {P_{\min }} = 2023\) khi m = 0 (thỏa mãn) Vậy P đạt giá trị nhỏ nhất bằng 2023 khi m = 0 2. Một đội xe dự định chở 120 tấn xi măng vào công trường. Khi chuẩn bị khởi hành thì đội xe được bổ sung thêm 5 chiếc xe nữa, nên cả đội đã chở thêm được 5 tấn và mỗi xe chở ít hơn so với dự định là 1 tấn xi măng. Hỏi theo dự định đội xe có bao nhiêu chiếc xe? Biết khối lượng xi măng mỗi xe chở là như nhau và mỗi xe chỉ chở đúng một chuyến. Giả sử theo dự định đội xe có x chiếc xe (\(x \in {N^*}\)). Khối lượng xi măng mỗi xe phải trở theo dự định là \(\frac{{120}}{x}\) tấn. Sau khi bổ sung 5 xe, số xe thực tế là \(x + 5\). Thực tế tổng khối lượng xi măng cả đội phải chở là 120 + 5 = 125 tấn. Khối lượng xi măng mỗi xe phải trở theo thực tế là \(\frac{{125}}{{x + 5}}\) tấn. Do mỗi xe chở ít hơn so với dự định là 1 tấn xi măng nên ta có phương trình: \(\begin{array}{l}\frac{{120}}{x} - \frac{{125}}{{x + 5}} = 1\\ \Leftrightarrow \frac{{120\left( {x + 5} \right)}}{{x\left( {x + 5} \right)}} - \frac{{125x}}{{x\left( {x + 5} \right)}} = 1\\ \Leftrightarrow \frac{{120\left( {x + 5} \right) - 125x}}{{x\left( {x + 5} \right)}} = 1\\ \Leftrightarrow \frac{{120x + 600 - 125x}}{{x\left( {x + 5} \right)}} = 1\\ \Leftrightarrow \frac{{600 - 5x}}{{{x^2} + 5x}} = 1\\ \Leftrightarrow 600 - 5x = {x^2} + 5x\\ \Leftrightarrow {x^2} + 10x - 600 = 0\\ \Leftrightarrow \left( {x - 20} \right)\left( {x + 30} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 20\left( {TM} \right)\\x = - 30\left( {KTM} \right)\end{array} \right.\end{array}\) Vậy theo dự định có tất cả 20 xe. Câu 4 (VD): Cách giải:
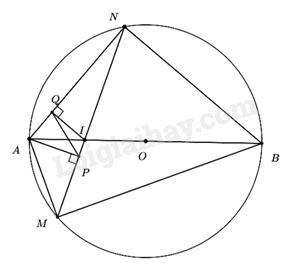
a) Tứ giác APIQ là tứ giác nội tiếp. Do \(IQ \bot AN\left( {gt} \right),AP \bot MN\left( {gt} \right) \Rightarrow \angle APN = \angle AQI = {90^0}\) Xét tứ giác AQIP có \(\angle API + \angle AQI = {90^0} + {90^0} = {180^0}\) Mà 2 góc này ở vị trí đối diện nên tứ giác AQIP nội tiếp (đhnb) (đpcm) b) PM.AI = MA.QI. Do tam giác APM vuông tại P nên \(\angle PAM + \angle AMP = {90^0}\) Ta có \(\angle ANB = \angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle NAB + \angle ABN = {90^0}\) Mà \(\angle ANM = \angle ABN\) (cùng chắn cung AN) \( \Rightarrow \angle NAB = \angle MAP\) hay \(\angle QAI = \angle PAM\) Xét \(\Delta AMP\) và \(\Delta AIQ\) có: \(\angle QAI = \angle PAM\) (chứng minh trên) \(\angle AQM = \angle AQI\left( { = {{90}^0}} \right)\) $\Rightarrow \Delta AMP\backsim \Delta AIQ\left( g.g \right)\Rightarrow \frac{AM}{AI}=\frac{PM}{IQ}\Leftrightarrow AM.IQ=AI.PM$ (đpcm) c) \(AM.BN + AN.BM \le 4{R^2}\) Xét \(\Delta AMP\) và \(\Delta ABN\) có: \(\angle APN = \angle ANB\left( { = {{90}^0}} \right)\) \(\angle MAP = \angle BAN\) (chứng minh trên) $\Rightarrow \Delta AMP\backsim \Delta ABN\left( g.g \right)\Rightarrow \frac{AM}{AB}=\frac{MP}{BN}\Rightarrow AM.BN=AB.MP$ (1) Xét \(\Delta APN\) và \(\Delta AMB\) có: \(\angle APN = \angle AMB\left( { = {{90}^0}} \right)\) \(\angle ANP = \angle ABM\) (cùng chắn cung AM) $\Rightarrow \Delta APN\backsim \Delta AMB\left( g.g \right)\Rightarrow \frac{AN}{AB}=\frac{PN}{MB}\Rightarrow AN.MB=AB.PN$ (2) Từ (1) và (2) suy ra \(AM.BN + AN.BM = AB.MP + AB.PN\) \( = AB\left( {MP + PN} \right) = AB.MN\) Mà \(MN \le AB\) (quan hệ đường kính va dây cung) \( \Rightarrow AB.MN \le AB.AB = 4{R^2}\) Vậy \(AM.BN + AN.BM \le 4{R^2}\) (đpcm) Câu 5 (VD): Phương pháp: 1. Đưa về phương trình nghiệm nguyên để giải. 2. Đưa về phương trình bậc hai tìm GTLN. Cách giải: 1. Tìm nghiệm nguyên của phương trình: \(2{x^2} + 3xy + {y^2} + 5x + 3y = 11\) \(\begin{array}{l}2{x^2} + 3xy + {y^2} + 5x + 3y = 11\\ \Leftrightarrow 2{x^2} + xy + x + 2xy + {y^2} + y + 4x + 2y + 2 = 13\\ \Leftrightarrow x\left( {2x + y + 1} \right) + y\left( {2x + y + 1} \right) + 2\left( {2x + y + 1} \right) = 13\\ \Leftrightarrow \left( {x + y + 2} \right)\left( {2x + y + 1} \right) = 13\end{array}\) Vì\(x,y\) là số nguyên nên\(x + y + 2\) và \(2x + y + 1\) là các ước của 13. TH1: \(\left\{ \begin{array}{l}x + y + 2 = 1\\2x + y + 1 = 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = - 1\\2x + y = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 13\\y = - 1 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 13\\y = - 14\end{array} \right.\) TH2: \(\left\{ \begin{array}{l}x + y + 2 = 13\\2x + y + 1 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = 11\\2x + y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 11\\y = - 2x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 11\\y = 22\end{array} \right.\) TH3: \(\left\{ \begin{array}{l}x + y + 2 = - 1\\2x + y + 1 = - 13\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = - 3\\2x + y = - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 11\\y = - 3 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 11\\y = 8\end{array} \right.\) TH4: \(\left\{ \begin{array}{l}x + y + 2 = - 13\\2x + y + 1 = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + y = - 15\\2x + y = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 13\\y = - 15 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 13\\y = - 28\end{array} \right.\) Vậy hệ phương trình có 4 nghiệm nguyên là: \(\left( {13; - 14} \right);\,\,\left( { - 11;22} \right);\,\left( { - 11;8} \right);\,\left( {13; - 28} \right)\) 2. Cho a, b là các số thực thỏa mãn \(4{a^2} - 2ab + {b^2} = 4a + 2b\). Tìm giá trị lớn nhất của biểu thức \(P = 253(2a + b)\). Gọi \(m = 2a + b \Rightarrow b = m - 2a\) Từ giả thiết: \(4{a^2} - 2ab + {b^2} = 4a + 2b\)(1) \(\begin{array}{l} \Rightarrow 4{a^2} - 2a\left( {m - 2a} \right) + {\left( {m - 2a} \right)^2} = 4a + 2\left( {m - 2a} \right)\\ \Leftrightarrow 4{a^2} - 2ma + 4{a^2} + {m^2} - 2ma + 4{a^2} = 4a + 2m - 4a\\ \Leftrightarrow 12{a^2} - 4ma + {m^2} - 2m = 0\end{array}\) Ta có: \(\Delta ' = {\left( {2m} \right)^2} - 12\left( {{m^2} - 2m} \right) = 4{m^2} - 12{m^2} + 24m = 24 - 8{m^2} = 8\left( {3 - {m^2}} \right)\) Để tồn tại số a thỏa mãn thì \(\Delta ' \ge 0 \Leftrightarrow 8\left( {3 - {m^2}} \right) \ge 0 \Leftrightarrow 3 - {m^2} \ge 0 \Leftrightarrow {m^2} \le 3 \Leftrightarrow - \sqrt 3 \le m \le \sqrt 3 \) \( \Rightarrow - 253\sqrt 3 \le P \le 253\sqrt 3 \) Vậy giá trị lớn nhất của P là \(253\sqrt 3 \), đạt được khi \(m = \sqrt 3 \Leftrightarrow 2a + b = \sqrt 3 \).
|