Đề thi vào 10 môn Toán Hậu Giang năm 2023

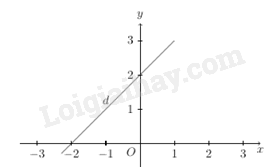
Đề bài

Phần I: Trắc nghiệm (3 điểm)

Câu 1: Giá trị của \(\sqrt 4 \) là

A. \( \pm 4\).

B. 16.

C. \(2\).

D. \( - 2\).

Câu 2: Giá trị của biểu thức \(A = \sqrt {27} {\rm{ \;}} - \sqrt 3 \) là

A. \(2\sqrt 6 \).

B. \(2\sqrt 3 \).

C. \(\sqrt {24} \).

D. \(3\sqrt 3 \).

Câu 3: Nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{4x - 5y = 23}\\{x + 2y = {\rm{ \;}} - 4}\end{array}} \right.\) là

A. \(\left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = {\rm{ \;}} - 2}\end{array}} \right.\).

B. \(\left\{ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 2}\\{y = 3}\end{array}} \right.\).

C. \(\left\{ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 3}\\{y = 2}\end{array}} \right.\).

D. \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = {\rm{ \;}} - 3}\end{array}} \right.\).

Câu 4: Giả sử \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) là nghiệm của phương trình \(2{x^2} - 3x - 7 = 0\). Giá trị của biểu thức \({x_1}.{x_2}\) bằng

A. \(\frac{3}{2}\) .

B. \( - \frac{3}{2}\).

C. \( - \frac{7}{2}\).

D. \(\frac{7}{2}\).

Câu 5: Số nào sau đây là nghiệm của phương trình \(3{x^4} - 10{x^2} - 8 = 0\)?

A. \(x = {\rm{ \;}} - 2\).

B. \(x = {\rm{ \;}} - \frac{2}{3}\).

C. \(x = 4\).

D. \(x = 16\)

Câu 6: Chu vi của đường tròn bán kính \(R = 4cm\) là

A. \(8\pi cm\).

B. \(4\pi cm\).

C. \(2\pi cm\).

D. \(16\pi cm\).

Câu 7: Cho hàm số \(y = ax + b\) có đồ thị là đường thẳng \(d\) như hình vẽ bên dưới

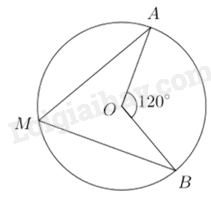
Điểm nào sau đây thuộc đường thẳng d?

A. \(A\left( {2;0} \right)\).

B. \(B\left( {0;2} \right)\).

C. \(C\left( {0; - 2} \right)\).

D. \(D\left( { - 2;2} \right)\).

Câu 8: Tứ giác nào sau đây nội tiếp được trong một đường tròn?

A. Hình thang vuông.

B. Hình bình hành.

C. Hình vuông.

D. Hình thoi.

Câu 9: Cho điểm \(M\) nằm trên đường tròn \(\left( O \right)\) và \(\angle AOB = 120^\circ \) như hình vẽ. Số đo của \(\angle AMB\) bằng

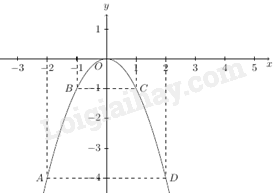
A. \(60^\circ \).

B. \(120^\circ \).

C. \(90^\circ \)

D. \(30^\circ \).

Câu 10: Một hình chữ nhật có chiều dài gấp đôi chiều rộng và có chu vi bằng 30cm. Diện tích của hình chữ nhật bằng

A. \(100c{m^2}\).

B. \(200c{m^2}\).

C. \(50c{m^2}\).

D. \(25c{m^2}\).

Câu 11: Một hình nón có bán kính đáy \(r = 3cm\) và độ dài đường sinh \(l = 5cm\). Diện tích xung quanh \({S_{xq}}\) của hình nón đã cho là

A. \({S_{xq}} = 12\pi c{m^2}\).

B. \({S_{xq}} = 8\pi c{m^2}\).

C. \({S_{xq}} = 30\pi c{m^2}\).

D. \({S_{xq}} = 15\pi c{m^2}\).

Câu 12: Hàm số nào sau đây có đồ thị như hình vẽ bên dưới?

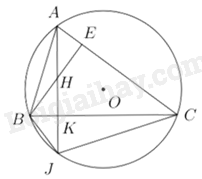
A. \(y = {\rm{ \;}} - {x^2}\).

B. \(y = {x^2}\).

C. \(y = {\rm{ \;}} - \frac{1}{2}{x^2}\)

D. \(y = {\rm{ \;}} - 2{x^2}\)

Phần II. Tự luận (7 điểm)

Câu 13: 

a) Tính giá trị của biểu thức \(A = \sqrt {625} {\rm{ \;}} - \sqrt {225} \)

b) Tìm điều kiện để biểu thức \(B = \sqrt {x - 1} \) có nghĩa. Tính giá trị của biểu thức \(B\) khi \(x = 10\)

c) Cho biểu thức \(C = \frac{2}{{\sqrt x {\rm{ \;}} - 3}} + \frac{1}{{\sqrt x {\rm{ \;}} + 3}} + \frac{{2\sqrt x {\rm{ \;}} - 3}}{{9 - x}}\), với \(x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 9\). Tìm \(x\) để \(C = {\rm{ \;}} - \frac{8}{5}\)

Câu 14: 

a) Giải phương trình \(2{x^2} - 5x - 3 = 0\)

b) Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = {\rm{ \;}} - 3}\\{3x - y = 5}\end{array}} \right.\)

Câu 15: Trong mặt phẳng với hệ tọa độ Oxy, cho hàm số \(y = 2{x^2}\) có đồ thị \(\left( P \right)\) và hàm số \(y = 3x - 1\) có đồ thị là đường thẳng \(\left( {\Delta {\rm{ \;}}} \right)\).

a) Vẽ đồ thị \(\left( P \right)\)

b) Tìm tọa độ giao điểm của đồ thị \(\left( P \right)\) và đường thẳng \(\left( {\Delta {\rm{ \;}}} \right)\) bằng phép tính

c) Tìm \(m\) để đường thẳng \(\left( d \right):y = {\rm{ \;}} - 2\left( {{m^2} - 2} \right)x - 2m + 6\) cắt đồ thị \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) thỏa mãn \(2{x_1}{x_2} - {\left( {{x_1} - {x_2}} \right)^2} = {\rm{ \;}} - 1\)

Câu 16: Cho tam giác ABC có ba góc nhọn, \(AB < AC\), nội tiếp đường tròn \(\left( O \right)\), các đường cao AK và BE cắt nhau tại \(H\).

a) Tính diện tích \(S\) của hình tròn \(\left( O \right)\), biết \(\left( O \right)\) có bán kính \(R = 5cm\)

b) Chứng minh tứ giác ABKE nội tiếp.

c) Gọi J là giao điểm của đường thẳng AK và đường tròn \(\left( O \right)\) (với \(J\) khác \(A\)). Chứng minh \(KH = KJ\)

Câu 17: Giải phương trình \(2{x^3} + x = \left( {2x + \frac{1}{2}} \right)\sqrt {x - \frac{1}{4}} \)

-----HẾT-----

Lời giải chi tiết

Phần I: Trắc nghiệm

Câu 1 (NB):

Phương pháp:

Sử dụng \(\sqrt {{a^2}} {\rm{ \;}} = \left| a \right|\)

Cách giải:

Ta có: \(\sqrt 4 {\rm{ \;}} = \sqrt {{2^2}} {\rm{ \;}} = 2\)

Chọn C.

Câu 2 (NB):

Phương pháp:

Sử dụng \(\sqrt {{a^2}} {\rm{ \;}} = \left| a \right|\)

Cách giải:

Ta có: \(A = \sqrt {27} {\rm{ \;}} - \sqrt 3 {\rm{ \;}} = 3\sqrt 3 {\rm{ \;}} - \sqrt 3 {\rm{ \;}} = 2\sqrt 3 \)

Chọn B.

Câu 3 (NB):

Phương pháp:

Giải hệ phương trình bằng phương pháp cộng đại số.

Cách giải:

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{4x - 5y = 23}\\{x + 2y = {\rm{ \;}} - 4}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4x - 5y = 23}\\{4x + 8y = {\rm{ \;}} - 16}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{13y = {\rm{ \;}} - 39}\\{4x - 5y = 23}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = {\rm{ \;}} - 3}\\{4x + 15 = 23}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = {\rm{ \;}} - 3}\end{array}} \right.\)

Chọn D.

Câu 4 (NB):

Phương pháp:

Sử dụng định lý Vi-ét \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - b}}{a}}\\{{x_1}{x_2} = \frac{c}{a}}\end{array}} \right.\)

Cách giải:

Sử dụng định lý Vi-ét ta có \({x_1}{x_2} = {\rm{ \;}} - \frac{7}{2}\)

Chọn C.

Câu 5 (TH):

Phương pháp:

Giải phương trình bằng phương pháp đưa về dạng tích A.B = 0

Cách giải:

Ta có: \(3{x^4} - 10{x^2} - 8 = 0 \Leftrightarrow \left( {{x^2} - 4} \right)\left( {{x^2} + \frac{2}{3}} \right) = 0 \Leftrightarrow {x^2} - 4 = 0{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} {x^2} + \frac{2}{3} > 0} \right) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 2}\\{x = {\rm{ \;}} - 2}\end{array}} \right.\)

Chọn A.

Câu 6 (NB):

Phương pháp:

Chu vi của đường tròn bán kính \(R\) là \(C = 2\pi R\)

Cách giải:

Chu vi của đường tròn bán kính \(R = 4cm\) là \(C = 2\pi .4 = 8\pi \left( {cm} \right)\)

Chọn A.

Câu 7 (NB):

Phương pháp:

Dựa vào đồ thị hàm số

Cách giải:

Dựa vào đồ thị hàm số ta thấy đồ thị hàm số đi qua điểm \(\left( {0;2} \right)\)

Chọn B.

Câu 8 (NB):

Phương pháp:

Hình vuông nội tiếp trong một đường tròn

Cách giải:

Hình vuông nội tiếp trong một đường tròn

Chọn C.

Câu 9 (TH):

Phương pháp:

Góc ở tâm bằng 2 lần góc nội tiếp cùng chắn một cung.

Cách giải:

Ta có: \(\angle AMB = \frac{1}{2}\angle AOB = \frac{1}{2}.120^\circ  = 60^\circ \)

Chọn A.

Câu 10 (TH):

Phương pháp:

Giải bài toán bằng cách lập hệ phương trình.

Cách giải:

Gọi chiều dài, chiều rộng hình chữ nhật lần lượt là \(a,{\mkern 1mu} {\mkern 1mu} b(a,b > 0)\)

Theo giả thiết \(\left\{ {\begin{array}{*{20}{l}}{a = 2b}\\{2\left( {a + b} \right) = 30}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2b}\\{a + b = 15}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 2b}\\{3b = 15}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 10}\\{b = 5}\end{array}} \right.\) (tm)

Diện tích hình chữ nhật là \(S = 10.5 = 50\left( {c{m^2}} \right)\)

Chọn C.

Câu 11 (TH):

Phương pháp:

Diện tích xung quanh của hình nón có bán kính đáy \(r\) và đường sinh \(l\) là \({S_{xq}} = \pi rl\)

Cách giải:

Diện tích xung quanh \({S_{xq}}\) của hình nón đã cho là \({S_{xq}} = \pi rl = \pi .3.5 = 15\pi {\mkern 1mu} {\mkern 1mu} \left( {c{m^2}} \right)\)

Chọn D.

Câu 12 (TH):

Phương pháp:

Đồ thị hàm số là đường cong parabol với \(y = a{x^2}{\mkern 1mu} {\mkern 1mu} \left( {a \ne 0} \right)\).

Dựa vào các điểm đi qua để tìm hàm số.

Cách giải:

Gọi hàm số cần tìm là \(y = a{x^2}{\mkern 1mu} {\mkern 1mu} \left( {a \ne 0} \right)\)

Ta thấy đồ thị hàm số đi qua điểm \(B\left( { - 1; - 1} \right),{\mkern 1mu} {\mkern 1mu} \) nên ta có:

\( - 1 = a.{( - 1)^2} \Rightarrow a = {\rm{ \;}} - 1\)

Vậy hàm số cần tìm là \(y = {\rm{ \;}} - {x^2}\)

Chọn A.

Phần II: Tự luận

Câu 13 (TH):

Phương pháp:

a) Tính toán với căn bậc hai.

b) ĐKXĐ của \(\sqrt A \) là \(A \ge 0\). Tìm x khi biết giá trị của biểu thức

c) Rút gọn biểu thức chứa căn bậc hai, tìm x khi biết giá trị của biểu thức

Cách giải:

a) Ta có: \(A = \sqrt {625} {\rm{ \;}} - \sqrt {225} {\rm{ \;}} = \sqrt {{{25}^2}} {\rm{ \;}} - \sqrt {{{15}^2}} {\rm{ \;}} = 25 - 15 = 10\)

Vậy \(A = 10\)

b) Để \(B = \sqrt {x - 1} \) có nghĩa thì \(x - 1 \ge 0 \Leftrightarrow x \ge 1\)

Khi \(x = 10\) thì \(B = \sqrt {10 - 1} {\rm{ \;}} = \sqrt 9 {\rm{ \;}} = 3\)

Vậy \(B = 3\) khi \(x = 10\)

c) Ta có:

\(\begin{array}{l}C = \frac{2}{{\sqrt x  - 3}} + \frac{1}{{\sqrt x  + 3}} + \frac{{2\sqrt x  - 3}}{{9 - x}},\,\,x \ge 0,\,\,x \ne 9\\C = \frac{{2\left( {\sqrt x  + 3} \right)}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}} + \frac{{\sqrt x  - 3}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}} + \frac{{3 - 2\sqrt x }}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\C = \frac{{2\sqrt x  + 6 + \sqrt x  - 3 + 3 - 2\sqrt x }}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\C = \frac{{\sqrt x  + 6}}{{\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 3} \right)}}\\C = \frac{{\sqrt x  + 6}}{{x - 9}}\end{array}\)

Để \(C = {\rm{ \;}} - \frac{8}{5}\)

\(\begin{array}{*{20}{l}}{ \Leftrightarrow \frac{{\sqrt x {\rm{ \;}} + 6}}{{x - 9}} = {\rm{ \;}} - \frac{8}{5}}\\{ \Leftrightarrow 5\sqrt x {\rm{ \;}} + 30 = {\rm{ \;}} - 8x + 72}\\{ \Leftrightarrow 8x + 5\sqrt x {\rm{ \;}} - 42 = 0}\\{ \Leftrightarrow \left( {\sqrt x {\rm{ \;}} - 2} \right)\left( {8\sqrt x {\rm{ \;}} + 21} \right) = 0}\\{ \Leftrightarrow \sqrt x {\rm{ \;}} = 2{\mkern 1mu} {\mkern 1mu} \left( {do{\mkern 1mu} {\mkern 1mu} 8\sqrt x {\rm{ \;}} + 21 > 0,{\mkern 1mu} {\mkern 1mu} \forall x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 9} \right)}\\{ \Leftrightarrow x = 4{\mkern 1mu} {\mkern 1mu} \left( {TM} \right)}\end{array}\)

Vậy để \(C = {\rm{ \;}} - \frac{8}{5}\) thì \(x = 4\)

Câu 14 (TH):

Phương pháp:

a) Giải phương trình bằng phương pháp đưa về dạng tích A.B = 0

b) Giải hệ phương trình bằng phương pháp cộng đại số.

Cách giải:

a) Ta có: \(2{x^2} - 5x - 3 = 0 \Leftrightarrow \left( {x - 3} \right)\left( {2x + 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 3 = 0}\\{2x + 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 3}\\{x = {\rm{ \;}} - \frac{1}{2}}\end{array}} \right.\)

Vậy tập nghiệm của phương trình là \(S = \left\{ {3; - \frac{1}{2}} \right\}\)

b) Ta có: \(\left\{ {\begin{array}{*{20}{l}}{x + 2y = {\rm{ \;}} - 3}\\{3x - y = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + 2y = {\rm{ \;}} - 3}\\{6x - 2y = 10}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x + 2y = {\rm{ \;}} - 3}\\{7x = 7}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 + 2y = {\rm{ \;}} - 3}\\{x = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = {\rm{ \;}} - 2}\end{array}} \right.\)

Vậy nghiệm của hệ phương trình là \(\left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = {\rm{ \;}} - 2}\end{array}} \right.\)

Câu 15 (VD):

Phương pháp:

a) Vẽ đồ thị dạng \(y = a{x^2}(a \ne 0)\)

b) Xét phương trình hoành độ giao điểm \(\left( P \right)\) và \(\left( {\Delta {\rm{ \;}}} \right)\).

c) Xét phương trình hoành độ giao điểm của (P) và (d).

Để (d) cắt (P) tại hai điểm phân biệt thì phương trình hoành độ giao điểm có 2 nghiệm phân biệt.

Thực hiện hệ thức.

Cách giải:

a) Ta có bảng giá trị sau:

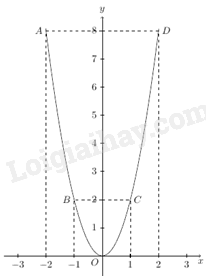
Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\left( {0;0} \right),{\mkern 1mu} {\mkern 1mu} A\left( { - 2;8} \right),{\mkern 1mu} {\mkern 1mu} B\left( { - 1;2} \right),\)

\(C\left( {1;2} \right),{\mkern 1mu} {\mkern 1mu} D\left( {2;8} \right)\)

Hệ số \(a = 2 > 0\) nên parabol có bề cong hướng lên trên

Đồ thị hàm số nhận Oy làm trục đối xứng

Ta vẽ được đồ thị hàm số \(y = 2{x^2}\) như sau:

b) Xét phương trình hoành độ giao điểm \(\left( P \right)\) và \(\left( {\Delta {\rm{ \;}}} \right)\) ta được

\(2{x^2} = 3x - 1 \Leftrightarrow 2{x^2} - 3x + 1 = 0 \Leftrightarrow \left( {2x - 1} \right)\left( {x - 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 1 = 0}\\{2x - 1 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = \frac{1}{2}}\end{array}} \right.\)

Với \(x = 1 \Rightarrow y = {2.1^2} = 2\)

Với \(x = \frac{1}{2} \Rightarrow y = 2.{\left( {\frac{1}{2}} \right)^2} = \frac{1}{2}\)

Vậy tọa độ 2 giao điểm của \(\left( P \right)\) và \(\left( {\Delta {\rm{ \;}}} \right)\) là \(\left( {1;2} \right),{\mkern 1mu} {\mkern 1mu} \left( {\frac{1}{2};\frac{1}{2}} \right)\)

c) Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) ta được:

\(\begin{array}{*{20}{l}}{2{x^2} = {\rm{ \;}} - 2\left( {m - 2} \right)x - 2m + 6}\\{ \Leftrightarrow 2{x^2} + 2\left( {m - 2} \right)x + 2m - 6 = 0}\\{ \Leftrightarrow {x^2} + \left( {m - 2} \right)x + m - 3 = 0{\mkern 1mu} {\mkern 1mu} \left( 1 \right)}\end{array}\)

Xét (1): \(\Delta {\rm{ \;}} = {\left( {m - 2} \right)^2} - 4\left( {m - 3} \right) = {m^2} - 5m + 7 = {\left( {m - \frac{5}{2}} \right)^2} + \frac{3}{4} > 0,{\mkern 1mu} {\mkern 1mu} \forall m \in \mathbb{R}\)

Do đó phương trình (1) luôn có 2 nghiệm phân biệt \({x_1},{\mkern 1mu} {\mkern 1mu} {x_2}\) với mọi \(m \in \mathbb{R}\)

Áp dụng định lý Vi-et ta được \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2 - m}\\{{x_1}{x_2} = m - 3}\end{array}} \right.\)

Ta có: \(2{x_1}{x_2} - {\left( {{x_1} - {x_2}} \right)^2} = {\rm{ \;}} - 1\)

\(\begin{array}{l} \Rightarrow 2{x_1}{x_2} - x_1^2 - x_2^2 + 2{x_1}{x_2} =  - 1\\ \Rightarrow  - x_1^2 - x_2^2 - 2{x_1}{x_2} + 6{x_1}{x_2} =  - 1\\ \Rightarrow  - {\left( {{x_1} + {x_2}} \right)^2} + 6{x_1}{x_2} =  - 1\\ \Rightarrow  - {\left( {2 - m} \right)^2} + 6\left( {m - 3} \right) =  - 1\\ \Rightarrow {\left( {2 - m} \right)^2} - 6\left( {m - 3} \right) - 1 = 0\\ \Rightarrow {m^2} - 10m + 21 = 0\\ \Rightarrow \left( {m - 7} \right)\left( {m - 3} \right) = 0\\ \Rightarrow \left[ \begin{array}{l}m - 7 = 0\\m - 3 = 0\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}m = 7\\m = 3\end{array} \right.\end{array}\)

Vậy \(m \in \left\{ {3;7} \right\}\)

Câu 16 (VD):

Phương pháp:

a) Diện tích \(S\) của hình tròn là \(S = 4\pi {R^2}\)

b) Chứng minh tứ giác ABKE nội tiếp theo dấu hiệu nhận biết: hai góc có đỉnh liên tiếp cùng nhìn một cạnh dưới một góc \(90^\circ \)

c) Chứng minh \(\Delta HBJ\) là tam giác cân tại B có \(BK\) vừa là đường cao vừa là đường trung tuyến.

Cách giải:

a) Diện tích \(S\) của hình tròn là \(S = 4\pi {R^2} = 4\pi {.5^2} = 100\pi \,\,\left( {c{m^2}} \right)\)

b) Ta có: \(\angle AEB = 90^\circ \,\,\left( {do\,\,BE \bot AC} \right)\)

\(\angle AKB = 90^\circ \,\,\left( {do\,\,AK \bot BC} \right)\)

Do đó \(\angle AEB = \angle AKB\)

Mà \(\angle AEB,\,\,\angle AKB\) cùng chắn cung \(AB\)

Suy ra \(AEKB\) là tứ giác nội tiếp

c) Ta có: \(AEKB\) là tứ giác nội tiếp

\( \Rightarrow \angle KAC = \angle HBK\)

Mà \(\angle KAC = \angle JBK\,\,\)(do ABJC nội tiếp đường tròn (O))

Nên \(\angle HBK = \angle JBK\)

Khi đó \(BK\) là phân giác của \(\angle HBJ\)

Xét \(\Delta HBJ\) có \(BK\) vừa là đường cao vừa là đường phân giác

\( \Rightarrow \Delta HBJ\) cân tại \(B\)

Mà \(BK\) là đường cao nên cũng là đường trung tuyến

Hay \(KH = KJ\) (đpcm)

Vậy \(KH = KJ\)

Câu 17 (VDC):

Phương pháp:

Tìm điều kiện xác định của biểu thức chứa căn.

Biến đổi đưa về dạng tích A.B = 0

Cách giải:

ĐKXĐ: \(x \ge \frac{1}{4}\)

Ta có:

\(\begin{array}{l}2{x^3} + x = \left( {2x + \frac{1}{2}} \right)\sqrt {x - \frac{1}{4}} \\ \Leftrightarrow 2{x^3} + x = \frac{1}{2}\left( {4x + 1} \right).\frac{1}{2}\sqrt {4x - 1} \\ \Leftrightarrow 8{x^3} + 4x = \left( {4x + 1} \right)\sqrt {4x - 1} \\ \Leftrightarrow {\left( {2x} \right)^3} + 2.2x = \left( {4x - 1} \right)\sqrt {4x - 1}  + 2\sqrt {4x - 1} \\ \Leftrightarrow \left[ {{{\left( {2x} \right)}^3} - {{\sqrt {4x - 1} }^3}} \right] + 2\left( {2x - \sqrt {4x - 1} } \right) = 0\\ \Leftrightarrow \left( {2x - \sqrt {4x - 1} } \right)\left( {4{x^2} + 2x\sqrt {4x - 1}  + 4x - 1} \right) + 2\left( {2x - \sqrt {4x - 1} } \right) = 0\\ \Leftrightarrow \left( {2x - \sqrt {4x - 1} } \right)\left( {4{x^2} + 2x\sqrt {4x - 1}  + 4x - 1 + 2} \right) = 0\\ \Leftrightarrow \left( {2x - \sqrt {4x - 1} } \right)\left( {4{x^2} + 2x\sqrt {4x - 1}  + 4x + 1} \right) = 0\\ \Leftrightarrow 2x - \sqrt {4x - 1}  = 0\,\,\left( {do\,\,x \ge \frac{1}{4} \Rightarrow 4{x^2} + 2x\sqrt {4x - 1}  + 4x + 1 > 0} \right)\end{array}\)

\(\begin{array}{l} \Leftrightarrow 2x = \sqrt {4x - 1} \\ \Leftrightarrow 4{x^2} = 4x - 1\\ \Leftrightarrow 4{x^2} - 4x + 1 = 0\\ \Leftrightarrow {\left( {2x - 1} \right)^2} = 0\\ \Leftrightarrow 2x - 1 = 0\\ \Leftrightarrow x = \frac{1}{2}\,\,\left( {TM} \right)\end{array}\)

Vậy \(x = \frac{1}{2}\)