Đề thi vào 10 môn Toán Hà Nam năm 2019

Đề bài

Câu I (2 điểm):

1) Giải phương trình: \({x^2} - 5x + 4 = 0\)

2) Giải hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 3\\2x + y = 7\end{array} \right..\)

Câu II (2 điểm):

1) Rút gọn biểu thức: \(A = \dfrac{4}{{\sqrt 5  - 1}} - 3\sqrt {45}  + \sqrt {{{\left( {\sqrt 5  - 1} \right)}^2}} .\)

2) Cho biểu thức: \(B = \left( {\dfrac{1}{{3 - \sqrt x }} - \dfrac{1}{{3 + \sqrt x }}} \right).\dfrac{{\sqrt x  + 3}}{{\sqrt x }}\,\,\,\,\left( {x > 0,\,\,\,x \ne 9} \right).\)

Rút gọn biểu thức \(B\) và tìm tất cả các giá trị nguyên của \(x\) để \(B > \dfrac{1}{2}.\)

Câu III (1,5 điểm):

Trong mặt phẳng tọa độ \(Oxy\) cho parabol \(\left( P \right):\,\,y = \dfrac{{{x^2}}}{2}\) và đường thẳng \(\left( d \right):\,\,y =  - mx + 3 - m\) (với \(m\) là tham số).

1) Tìm tọa độ điểm \(M\) thuộc parabol \(\left( P \right),\) biết điểm \(M\) có hoành độ bằng \(4.\)

2) Chứng minh đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt \(A,\,\,B.\) Gọi \({x_1},\,\,{x_2}\) lần lượt là hoành hoành độ của hai điểm \(A,\,\,B.\) Tìm \(m\) để \(x_1^2 + x_2^2 = 2{x_1}{x_2} + 20.\)

Câu IV (4,0 điểm)

1) Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(AB\). Trên cùng nửa mặt phẳng bờ \(AB\) chứa nửa đường tròn \(\left( {O;R} \right)\)  vẽ các tiếp tuyến \(Ax,\,\,By\) với nửa đường tròn đó. Gọi \(M\) là một điểm bất kì trên nửa đường tròn \(\left( {O;R} \right)\) (với \(M\) khác \(A\), \(M\) khác \(B\)), tiếp tuyến của nửa đường tròn tại \(M\)cắt \(Ax,\,\,By\) lần lượt tại \(C\) và \(D\).

a) Chứng minh tứ giác \(ACMO\) nội tiếp.

b) Chứng minh tam giác \(COD\) vuông tại \(O\).

c) Chứng minh \(AC.BD = {R^2}\).

d) Kẻ \(MN \bot AB\,\,\left( {N \in AB} \right)\); \(BC\) cắt \(MN\) tại \(I\). Chứng minh \(I\) là trung điểm của \(MN\).

2) Tính thể tích của một hình nón có bán kính đáy \(r = 4cm\), độ dài đường sinh \(l = 5cm\).

Câu V (0,5 điểm):

Cho \(a,\,\,b,\,\,c\) là các số thực dương và thỏa mãn điều kiện \(abc = 1.\)

Chứng minh \(\dfrac{1}{{2 + a}} + \dfrac{1}{{2 + b}} + \dfrac{1}{{2 + c}} \le 1.\)

Lời giải

Câu I (VD)

Phương pháp:

1) Giải phương trình bằng cách nhẩm nghiệm hoặc đưa về phương trình tích.

2) Giải hệ phương trình bằng phương pháp cộng đại số.

Cách giải:

1) Giải phương trình: \({x^2} - 5x + 4 = 0\)

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,{x^2} - 5x + 4 = 0\\ \Leftrightarrow {x^2} - 4x - x + 4 = 0\\ \Leftrightarrow x\left( {x - 4} \right) - \left( {x - 4} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right..\end{array}\)

Vậy phương trình có tập nghiệm \(S = \left\{ {1;\,\,4} \right\}.\)

2) Giải hệ phương trình: \(\left\{ \begin{array}{l}3x - y = 3\\2x + y = 7\end{array} \right..\)

\(\left\{ \begin{array}{l}3x - y = 3\\2x + y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x = 10\\y = 3x - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3.2 - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right..\)

Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\,\,y} \right) = \left( {2;\,\,3} \right).\)  

Câu II (VD)

Phương pháp:

1) Sử dụng các công thức  \(\dfrac{A}{{\sqrt B  - C}} = \dfrac{{A\left( {\sqrt B  + C} \right)}}{{B - {C^2}}};\,\,\,\sqrt {{A^2}B}  = \left| A \right|\sqrt B  = \left\{ \begin{array}{l}A\,\sqrt B \,\,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,\,khi\,\,\,A < 0\end{array} \right.\)  để làm bài.

2) Quy đồng mẫu các phân thức rồi rút gọn biểu thức.

+) Giải bất phương trình \(B > \dfrac{1}{2}\) để tìm \(x.\) Đối chiếu với điều kiện của \(x\) và điều kiện \(x\) nguyên rồi kết luận.

Cách giải:

1) Rút gọn biểu thức: \(A = \dfrac{4}{{\sqrt 5  - 1}} - 3\sqrt {45}  + \sqrt {{{\left( {\sqrt 5  - 1} \right)}^2}} .\)

\(\begin{array}{l}A = \dfrac{4}{{\sqrt 5  - 1}} - 3\sqrt {45}  + \sqrt {{{\left( {\sqrt 5  - 1} \right)}^2}} \\\,\,\,\,\,\, = \dfrac{{4\left( {\sqrt 5  + 1} \right)}}{{5 - 1}} - 3\sqrt {{3^2}.5}  + \left| {\sqrt 5  - 1} \right|\\\,\,\,\,\,\, = \sqrt 5  + 1 - 9\sqrt 5  + \sqrt 5  - 1\,\,\,\,\,\left( {do\,\,\,\,\sqrt 5  - 1 > 0} \right)\\\,\,\,\,\,\, =  - 7\sqrt 5 .\end{array}\)

Vậy \(A =  - 7\sqrt 5 .\)

2) Cho biểu thức: \(B = \left( {\dfrac{1}{{3 - \sqrt x }} - \dfrac{1}{{3 + \sqrt x }}} \right).\dfrac{{\sqrt x  + 3}}{{\sqrt x }}\,\,\,\,\left( {x > 0,\,\,\,x \ne 9} \right).\)

Rút gọn biểu thức \(B\) và tìm tất cả các giá trị nguyên của \(x\) để \(B > \dfrac{1}{2}.\)

Điều kiện: \(x > 0,\,\,\,x \ne 9.\)

\(\begin{array}{l}B = \left( {\dfrac{1}{{3 - \sqrt x }} - \dfrac{1}{{3 + \sqrt x }}} \right).\dfrac{{\sqrt x  + 3}}{{\sqrt x }}\,\,\,\\\,\,\,\, = \dfrac{{3 + \sqrt x  - 3 + \sqrt x }}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}}.\dfrac{{\sqrt x  + 3}}{{\sqrt x }}\\\,\,\,\, = \dfrac{{2\sqrt x }}{{3 - \sqrt x }}.\dfrac{1}{{\sqrt x }} = \dfrac{2}{{3 - \sqrt x }}.\end{array}\)

Ta có: \(B > \dfrac{1}{2} \Leftrightarrow \dfrac{2}{{3 - \sqrt x }} > \dfrac{1}{2}\)

\(\begin{array}{l} \Leftrightarrow \dfrac{2}{{3 - \sqrt x }} - \dfrac{1}{2} > 0 \Leftrightarrow \dfrac{{4 - 3 + \sqrt x }}{{2\left( {3 - \sqrt x } \right)}} > 0\\ \Leftrightarrow \dfrac{{\sqrt x  + 1}}{{2\left( {3 - \sqrt x } \right)}} > 0 \Leftrightarrow 3 - \sqrt x  > 0\,\,\,\,\,\left( {do\,\,\,\sqrt x  + 1 > 0\,\,\,\forall x \ge 0} \right)\\ \Leftrightarrow \sqrt x  < 3 \Leftrightarrow x < 9.\end{array}\)

Kết hợp với điều kiện \(x > 0,\,\,\,x \ne 9,\,\,\,x \in \mathbb{Z} \Rightarrow x \in \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7;\,\,8} \right\}.\)

Vậy \(x \in \left\{ {\,1;\,\,2;\,\,3;\,\,4;\,\,5;\,\,6;\,\,7;\,\,8} \right\}\) thì \(B > \dfrac{1}{2}.\)

Câu III (VD)

Phương pháp:

1) Thay hoành độ điểm \(M\) vào công thức \(y = \dfrac{1}{2}{x^2}\) để tìm tung độ của điểm \(M.\)

2) Xét phương trình hoành độ giao điểm \(\left( * \right)\)  của hai đồ thị hàm số.

+) Đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta  > 0\,\,\,\left( {\Delta ' > 0} \right).\)

+) Sử dụng định lý Vi-et và hệ thức bài cho để tìm \(m.\) Đối chiếu với điều kiện rồi kết luận.

Cách giải:

Trong mặt phẳng tọa độ \(Oxy\) cho parabol \(\left( P \right):\,\,y = \dfrac{{{x^2}}}{2}\) và đường thẳng \(\left( d \right):\,\,y =  - mx + 3 - m\) (với \(m\) là tham số).

1) Tìm tọa độ điểm \(M\) thuộc parabol \(\left( P \right),\) biết điểm \(M\) có hoành độ bằng \(4.\)

Ta có \(M\left( {4;\,\,{y_M}} \right)\) thuộc \(\left( P \right):\,\,\,y = \dfrac{{{x^2}}}{2}\) nên thay \(x = 4\) vào công thức hàm số \(y = \dfrac{1}{2}{x^2}\) ta được:

\({y_M} = \dfrac{1}{2}{.4^2} = 8 \Rightarrow M\left( {4;\,\,8} \right).\)

Vậy \(M\left( {4;\,\,8} \right).\)

2) Chứng minh đường thẳng \(\left( d \right)\) luôn cắt parabol \(\left( P \right)\) tại hai điểm phân biệt \(A,\,\,B.\) Gọi \({x_1},\,\,{x_2}\) lần lượt là hoành hoành độ của hai điểm \(A,\,\,B.\) Tìm \(m\) để \(x_1^2 + x_2^2 = 2{x_1}{x_2} + 20.\)

Phương trình hoành độ giao điểm của hai đồ thị hàm số là:

\(\dfrac{{{x^2}}}{2} =  - mx + 3 - m \Leftrightarrow {x^2} + 2mx + 2m - 6 = 0\,\,\,\,\left( * \right)\)

Đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt

\( \Leftrightarrow \Delta ' > 0 \Leftrightarrow {m^2} - 2m + 6 > 0\, \Leftrightarrow {m^2} - 2m + 1 + 5 > 0 \Leftrightarrow {\left( {m - 1} \right)^2} + 5 > 0\,\,\,\forall m\)

\( \Rightarrow \) Đường thẳng \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_1};\,\,{y_1}} \right),\,\,\,B\left( {{x_2};\,\,{y_2}} \right).\)

Áp dụng định lý Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 2m\\{x_1}{x_2} = 2m - 6\end{array} \right..\)

Theo đề bài ta có: \(x_1^2 + x_2^2 = 2{x_1}{x_2} + 20\)

\(\begin{array}{l} \Leftrightarrow x_1^2 + x_2^2 + 2{x_1}{x_2} - 4{x_1}{x_2} - 20 = 0\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} - 20 = 0\\ \Leftrightarrow {\left( { - 2m} \right)^2} - 4\left( {2m - 6} \right) - 20 = 0\\ \Leftrightarrow 4{m^2} - 8m + 24 - 20 = 0\\ \Leftrightarrow 4{m^2} - 8m + 4 = 0\\ \Leftrightarrow {m^2} - 2m + 1 = 0\\ \Leftrightarrow {\left( {m - 1} \right)^2} = 0\\ \Leftrightarrow m - 1 = 0\\ \Leftrightarrow m = 1.\end{array}\)

Vậy \(m = 1\) thỏa mãn bài toán.

Câu IV (4,0 điểm) (VD)

Phương pháp:

1) a) Chứng minh tứ giác \(ACMO\) là tứ giác có tổng hai góc đối bằng \({180^0}\).

b) Áp dụng tính chất : hai tia phân giác của 2 góc kề bù vuông góc với nhau.

c) Áp dụng hệ thức lượng trong tam giác vuông và tính chất 2 tiếp tuyến cắt nhau.

d) Áp dụng tính chất đường phân giác.

2) Tính chiều cao của hình nón bằng định lý Pitago: \(h = \sqrt {{l^2} - {r^2}} .\)

+) Thể tích hình nón có bán kính đáy \(r\) và chiều cao \(h\) là: \(V = \dfrac{1}{3}\pi {r^2}h.\)

Cách giải:

 

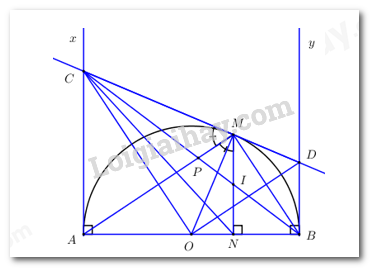
1) a) Chứng minh tứ giác \(ACMO\) nội tiếp.

Do \(AC\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A \Rightarrow \angle OAC = {90^0}\).

      \(MC\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(M \Rightarrow \angle OMC = {90^0}\).

Xét tứ giác \(ACMO\) có: \(\angle OAC + \angle OMC = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(ACMO\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).

b) Chứng minh tam giác \(COD\) vuông tại \(O\).    

Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có:

\(OC\) là tia phân giác của \(\angle AOM\);

\(OD\) là tia phân giác của \(\angle BOM\);

Mà \(\angle AOM;\,\,\angle BOM\) là hai góc kề bù \( \Rightarrow OC \bot OD\) (hai tia phân giác của 2 góc kề bù vuông góc với nhau).

\( \Rightarrow \angle COD = {90^0}\) hay tam giác \(COD\) vuông tại \(O\). (đpcm)

c) Chứng minh \(AC.BD = {R^2}\).

Áp dụng hệ thức lượng trong tam giác vuông \(OCD\) vuông tại \(O\) có đường cao \(OM\) ta có: \(O{M^2} = MC.MD\).

Mà \(OM = R \Rightarrow MC.MD = {R^2}\) (1).

Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có: \(AC = MC;\,\,BD = MD\) (2).

Từ (1) và (2) suy ra \(AC.BD = {R^2}\). (đpcm)

d) Kẻ \(MN \bot AB\,\,\left( {N \in AB} \right)\); \(BC\) cắt \(MN\) tại \(I\). Chứng minh \(I\) là trung điểm của \(MN\).

Ta có: \(\left\{ \begin{array}{l}AC \bot AB\\BD \bot AB\\MN \bot AB\end{array} \right.\,\,\left( {gt} \right) \Rightarrow AC//BD//MN\) (Từ vuông góc đến song song).

Gọi \(P = AM \cap CN\). Áp dụng định lí Ta-lét ta có : \(\dfrac{{MI}}{{AC}} = \dfrac{{PI}}{{PC}};\,\,\dfrac{{NI}}{{AC}} = \dfrac{{BI}}{{BC}}\) (3).

Ta có : \(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle AMN + \angle NMB = {90^0}\).

Mà trong tam giác vuông \(MNB\) lại có: \(\angle NBM + \angle NMB = {90^0}\)

\( \Rightarrow \angle AMN = \angle NBM = \angle ABM\).

Ta có : \(\angle ABM = \angle AMC\) (góc nội tiếp và tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AM\)) ;

           \(\angle ABM = \angle AMN\) (cmt) ;

\( \Rightarrow \angle AMC = \angle AMN \Rightarrow MA\) là tia phân giác trong của góc \(CMN\).

Mà \(MB \bot MA\,\,\left( {\angle AMB = {{90}^0}} \right) \Rightarrow MB\) là tia phân giác ngoài của góc \(CMN\).

Áp dụng tính chất đường phân giác trong tam giác \(CMI\) ta có: \(\dfrac{{MI}}{{MC}} = \dfrac{{PI}}{{PC}} = \dfrac{{BI}}{{BC}}\)  (4)

Từ (3) và (4) \( \Rightarrow \dfrac{{MI}}{{AC}} = \dfrac{{NI}}{{AC}} \Leftrightarrow MI = NI\).

Vậy \(I\) là trung điểm của \(MN\) (đpcm).

2) Chiều cao của hình nón là: \(h = \sqrt {{l^2} - {r^2}}  = \sqrt {{5^2} - {4^2}}  = \sqrt 9  = 3\,\,\left( {cm} \right).\)

Thể tích của hình nón đã cho là: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.4^2}.3 = 16\pi \,\,\left( {c{m^3}} \right).\)

Câu V (VDC)

Cách giải:

Ta có: \(\dfrac{1}{{2 + a}} = \dfrac{{abc}}{{2abc + a}} = \dfrac{{bc}}{{2bc + 1}}\,\,\left( {Do\,\,a > 0} \right)\).

Áp dụng BĐT Cô-si ta có: \(2bc + 1 = bc + bc + 1 \ge 3\sqrt[3]{{{{\left( {bc} \right)}^2}}} \Rightarrow \dfrac{{bc}}{{2bc + 1}} \le \dfrac{{bc}}{{3\sqrt[3]{{{{\left( {bc} \right)}^2}}}}} = \dfrac{{\sqrt[3]{{bc}}}}{3}\)\( \Rightarrow \dfrac{1}{{2 + a}} \le \dfrac{{\sqrt[3]{{bc}}}}{3}\)

CMTT ta có : \(\dfrac{1}{{2 + b}} \le \dfrac{{\sqrt[3]{{ca}}}}{3};\,\,\dfrac{1}{{2 + c}} \le \dfrac{{\sqrt[3]{{ab}}}}{3}\,\)

Cộng vế với vế ta được \(\dfrac{1}{{2 + a}} + \dfrac{1}{{2 + b}} + \dfrac{1}{{2 + c}} \le \dfrac{1}{3}\left( {\sqrt[3]{{ab}} + \sqrt[3]{{bc}} + \sqrt[3]{{ca}}} \right) = \dfrac{1}{3}\left( {\dfrac{1}{{\sqrt[3]{a}}} + \dfrac{1}{{\sqrt[3]{b}}} + \dfrac{1}{{\sqrt[3]{c}}}} \right)\).

Ta có : \(\dfrac{1}{{\sqrt[3]{a}}} + \dfrac{1}{{\sqrt[3]{b}}} + \dfrac{1}{{\sqrt[3]{c}}} \le \dfrac{9}{{\sqrt[3]{a} + \sqrt[3]{b} + \sqrt[3]{c}}} \le \dfrac{9}{{3\sqrt[3]{{\sqrt[3]{{abc}}}}}} = \dfrac{9}{3} = 3\).

\( \Rightarrow \dfrac{1}{{\sqrt[3]{a}}} + \dfrac{1}{{\sqrt[3]{b}}} + \dfrac{1}{{\sqrt[3]{c}}} \le 3 \Rightarrow 3\left( {\dfrac{1}{{\sqrt[3]{a}}} + \dfrac{1}{{\sqrt[3]{b}}} + \dfrac{1}{{\sqrt[3]{c}}}} \right) \le 1\).

Vậy \(\dfrac{1}{{2 + a}} + \dfrac{1}{{2 + b}} + \dfrac{1}{{2 + c}} \le 1.\) Dấu "=" xảy ra \( \Leftrightarrow a = b = c = 1\).