Đề thi vào 10 môn Toán Đồng Nai năm 2020Tải vềCâu 1: 1) Giải hệ phương trình:
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
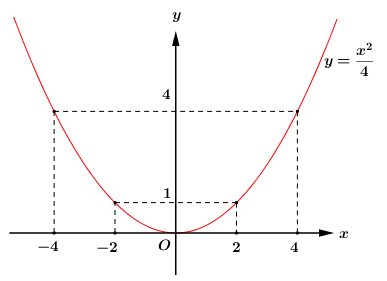
Đề bài Câu 1: 1) Giải hệ phương trình: \(\left\{ \begin{array}{l}3x - 5y = 7\\2x + 4y = 1\end{array} \right..\) 2) Giải phương trình \({x^4} - 12{x^2} + 16 = 0.\) 3) Giải phương trình \(\dfrac{1}{{x - 1}} + \dfrac{1}{{\left( {x - 1} \right)\left( {x - 2} \right)}} = \dfrac{3}{{2x}}.\) Câu 2: 1) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = \dfrac{{{x^2}}}{4}\). 2) Tìm các tham số thực m để hai đường thẳng \(y = 2x\) và \(y = \left( {{m^2} + m} \right)x + 1\) cắt nhau. 3) Tìm các số thực a để biểu thức \(\dfrac{1}{{\sqrt {a - 2} }} + \sqrt {6 - 2a} \) xác định. Câu 3: 1) Cho một hình cầu có thể tích bằng \(288\pi \,\,\left( {c{m^3}} \right)\). Tính diện tích của mặt cầu. 2) Một nhóm học sinh được giao sắp xếp 270 quyển sách vào tủ ở thư viện trong một thời gian nhất định. Khi bắt đầu làm việc nhóm được bổ sung thêm học sinh nên mỗi giờ nhóm sắp xếp được nhiều hơn dự định 20 quyển sách, vì vậy không những hoàn thành trước dự định 1 giờ mà còn vượt mức được 10 quyển sách. Hỏi số quyển sách mỗi giờ nhóm dự định sắp xếp là bao nhiêu? 3) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 2x - 1 = 0\). Hãy lập một phương trình bậc hai một ẩn có hai nghiệm là \(\left| {{{\left( {{x_1}} \right)}^3}} \right|\), \(\left| {{{\left( {{x_2}} \right)}^3}} \right|\). Câu 4: 1) Rút gọn biểu thức \(P = \left( {\dfrac{{a\sqrt a - 8}}{{a + 2\sqrt a + 4}}} \right)\left( {\dfrac{{a + 5\sqrt a + 6}}{{a - 4}}} \right)\) (với \(a \ge 0\) và \(a \ne 4\)) 2) Tìm các số thực \(x\) và \(y\) thỏa mãn \(\left\{ \begin{array}{l}{x^3} = {y^2} + 18\\{y^3} = {x^2} + 18\end{array} \right.\). Câu 5: Cho \(\Delta ABC\) nhọn nội tiếp đường tròn \(\left( O \right)\) có hai đường cao \(BE\) và \(CF\) cắt nhau tại trực tâm \(H,\,\,AB < AC.\) Vẽ đường kính \(AD\) của \(\left( O \right).\) Gọi \(K\) là giao điểm của đường thẳng \(AH\) với đường tròn \(\left( O \right),\,\,\,K \ne A.\) Gọi \(L,\,\,P\) lần lượt là giao điểm của hai đường thẳng \(BC\) và \(EF,\,\,AC\) và \(KD.\) 1) Chứng minh tứ giác \(EHKP\) nội tiếp đường tròn và tâm \(I\) của đường tròn này thuộc đường thẳng \(BC.\) 2) Gọi \(M\) là trung điểm của đoạn thẳng \(BC.\) Chứng minh \(AH = 2OM.\) 3) Gọi \(T\) là giao điểm của đường tròn \(\left( O \right)\) với đường tròn ngoại tiếp \(\Delta EFK,\,\,\,T \ne K.\)Chứng minh rằng ba điểm \(L,\,\,K,\,\,T\) thẳng hàng. Câu 6: Cho ba số thực dương \(a,\,\,b,\,\,c\) thỏa mãn \(abc = 1\). Chứng minh rằng \({\left( {{a^2} + {b^2} + {c^2}} \right)^3} \ge 9\left( {a + b + c} \right)\). Lời giải chi tiết Câu 1 (1,75 điểm) Cách giải: 1) Giải hệ phương trình: \(\left\{ \begin{array}{l}3x - 5y = 7\\2x + 4y = 1\end{array} \right..\) \(\left\{ \begin{array}{l}3x - 5y = 7\\2x + 4y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}6x - 10y = 14\\6x + 12y = 3\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}22y = - 11\\2x + 4y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = - \dfrac{1}{2}\\2x + 4.\left( { - \dfrac{1}{2}} \right) = 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}2x - 2 = 1\\y = - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{3}{2}\\y = - \dfrac{1}{2}\end{array} \right.\) Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\,\,y} \right) = \left( {\dfrac{3}{2}; - \dfrac{1}{2}} \right).\) 2) Giải phương trình \({x^4} - 12{x^2} + 16 = 0.\) Đặt \({x^2} = t\,\,\left( {t \ge 0} \right).\) Khi đó ta có phương trình \( \Leftrightarrow {t^2} - 12t + 16 = 0\) Phương trình có: \(\Delta ' = {6^2} - 16 = 20 > 0\) \( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{t_1} = 6 - \sqrt {20} = 6 - 2\sqrt 5 \,\,\left( {tm} \right)\\{t_2} = 6 + \sqrt {20} = 6 + 2\sqrt 5 \,\,\,\left( {tm} \right)\end{array} \right..\) +) Với \(t = 6 - 2\sqrt 5 \) \( \Leftrightarrow {x^2} = 6 - 2\sqrt 5 \) \(\begin{array}{l} \Leftrightarrow {x^2} = {\left( {\sqrt 5 } \right)^2} - 2\sqrt 5 + 1\\ \Leftrightarrow {x^2} = {\left( {\sqrt 5 - 1} \right)^2} \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 5 - 1\\x = 1 - \sqrt 5 \end{array} \right..\,\,\,\end{array}\) +) Với \(t = 6 + 2\sqrt 5 \) \( \Leftrightarrow {x^2} = 6 + 2\sqrt 5 \) \(\begin{array}{l} \Leftrightarrow {x^2} = {\left( {\sqrt 5 } \right)^2} + 2\sqrt 5 + 1\\ \Leftrightarrow {x^2} = {\left( {\sqrt 5 + 1} \right)^2} \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 5 + 1\\x = - \sqrt 5 - 1\end{array} \right..\,\,\,\end{array}\) Vậy tập nghiệm của phương trình đã cho là: \(S = \left\{ { - \sqrt 5 - 1;\,\,1 - \sqrt 5 ;\,\,\,\sqrt 5 - 1;\,\,\sqrt 5 + 1} \right\}.\) 3) Giải phương trình \(\dfrac{1}{{x - 1}} + \dfrac{1}{{\left( {x - 1} \right)\left( {x - 2} \right)}} = \dfrac{3}{{2x}}.\) Điều kiện: \(\left\{ \begin{array}{l}x \ne 0\\x \ne 1\\x \ne 2\end{array} \right..\) \(\begin{array}{l}\,\,\,\,\dfrac{1}{{x - 1}} + \dfrac{1}{{\left( {x - 1} \right)\left( {x - 2} \right)}} = \dfrac{3}{{2x}}\\ \Rightarrow 2x\left( {x - 2} \right) + 2x = 3\left( {x - 1} \right)\left( {x - 2} \right)\\ \Leftrightarrow 2{x^2} - 4x + 2x = 3{x^2} - 9x + 6\\ \Leftrightarrow {x^2} - 7x + 6 = 0\\ \Leftrightarrow {x^2} - 6x - x + 6 = 0\\ \Leftrightarrow x\left( {x - 6} \right) - \left( {x - 6} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 6 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\left( {ktm} \right)\\x = 6\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy tập nghiệm của phương trình đã cho là:\(S = \left\{ 6 \right\}.\) Câu 2 (2 điểm) Cách giải: 1) Vẽ đồ thị \(\left( P \right)\) của hàm số \(y = \dfrac{{{x^2}}}{4}\). Ta có bảng giá trị:
Do đó, parabol \(\left( P \right):\,\,\,y = \dfrac{{{x^2}}}{4}\) là đường cong đi qua các điểm \(\left( { - 4;4} \right)\), \(\left( { - 2;1} \right)\), \(\left( {0;0} \right)\), \(\left( {2;1} \right)\), \(\left( {4;4} \right)\) và nhận \(Oy\) làm trục đối xứng. Đồ thị hàm số:
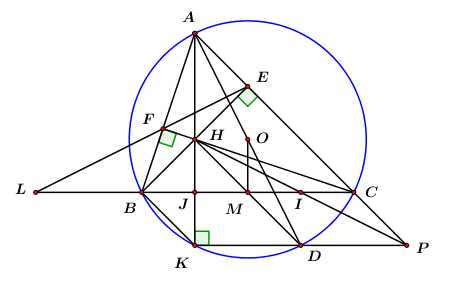
2) Tìm các tham số thực m để hai đường thẳng \(y = 2x\) và \(y = \left( {{m^2} + m} \right)x + 1\) cắt nhau. Hai đường thẳng \(y = 2x\) và \(y = \left( {{m^2} + m} \right)x + 1\) cắt nhau khi và chi khi: \(\begin{array}{l}\,\,\,\,\,\,\,{m^2} + m \ne 2\\ \Leftrightarrow {m^2} + m - 2 \ne 0\\ \Leftrightarrow {m^2} - m + 2m - 2 \ne 0\\ \Leftrightarrow m\left( {m - 1} \right) + 2\left( {m - 1} \right) \ne 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 2} \right) \ne 0\\ \Leftrightarrow \left\{ \begin{array}{l}m - 1 \ne 0\\m + 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 1\\m \ne - 2\end{array} \right.\end{array}\) Vậy với \(m \ne 1\) và \(m \ne - 2\) thì hai đường thẳng \(y = 2x\) và \(y = \left( {{m^2} + m} \right)x + 1\) cắt nhau. 3) Tìm các số thực a để biểu thức \(\dfrac{1}{{\sqrt {a - 2} }} + \sqrt {6 - 2a} \) xác định. Biểu thức \(\dfrac{1}{{\sqrt {a - 2} }} + \sqrt {6 - 2a} \) xác định \( \Leftrightarrow \left\{ \begin{array}{l}a - 2 > 0\\6 - 2a \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a > 2\\a \le 3\end{array} \right. \Leftrightarrow 2 < a \le 3\). Vậy với \(2 < a \le 3\) thì biểu thức \(\dfrac{1}{{\sqrt {a - 2} }} + \sqrt {6 - 2a} \) xác định. Câu 3 (1,75 điểm) Cách giải: 1) Cho một hình cầu có thể tích bằng \(288\pi \,\,\left( {c{m^3}} \right)\). Tính diện tích của mặt cầu. Gọi \(R\) là bán kính của hình cầu. Vì khối cầu có thể tích bằng \(288\pi \,\,\left( {c{m^3}} \right)\) nên \(\dfrac{4}{3}\pi {R^3} = 288\pi \Leftrightarrow {R^3} = 216\) \( \Leftrightarrow R = \sqrt[3]{{216}} = 6\,\,\left( {cm} \right)\). Vậy diện tích mặt cầu là \(S = 4\pi {R^2} = 4\pi {.6^2} = 144\pi \,\,\left( {c{m^2}} \right)\). 2) Một nhóm học sinh được giao sắp xếp 270 quyển sách vào tủ ở thư viện trong một thời gian nhất định. Khi bắt đầu làm việc nhóm được bổ sung thêm học sinh nên mỗi giờ nhóm sắp xếp được nhiều hơn dự định 20 quyển sách, vì vậy không những hoàn thành trước dự định 1 giờ mà còn vượt mức được 10 quyển sách. Hỏi số quyển sách mỗi giờ nhóm dự định sắp xếp là bao nhiêu? Gọi số quyển sách mỗi giờ nhóm dự định sắp xếp là \(x\) (quyển) (ĐK: \(x \in {\mathbb{N}^*}\)). \( \Rightarrow \) Thời gian dự định sắp xếp xong 270 quyển sách là \(\dfrac{{270}}{x}\,\,\left( h \right)\). Vì mỗi giờ nhóm sắp xếp được nhiều hơn dự định 20 quyển sách nên thực tế số quyển sách mỗi giờ nhóm đã sắp xếp được là \(x + 20\) (quyển). Vì nhóm sắp xếp vượt mức được giao 10 quyển sách nên nhóm đó đã sắp xếp được \(270 + 10 = 280\) (quyển) \( \Rightarrow \) Thời gian thực tế sắp xếp xong 280 quyển sách là: \(\dfrac{{280}}{{x + 20}}\,\,\left( h \right)\). Vì thực tế hoàn thành trước dự định 1 giờ nên ta có phương trình: \(\begin{array}{l}\,\,\,\,\,\dfrac{{270}}{x} - \dfrac{{280}}{{x + 20}} = 1\\ \Leftrightarrow 270\left( {x + 20} \right) - 280x = x\left( {x + 20} \right)\\ \Leftrightarrow 270x + 5400 - 280x = {x^2} + 20x\\ \Leftrightarrow {x^2} + 30x - 5400 = 0\\ \Leftrightarrow {x^2} - 60x + 90x - 5400 = 0\\ \Leftrightarrow x\left( {x - 60} \right) + 90\left( {x - 60} \right) = 0\\ \Leftrightarrow \left( {x - 60} \right)\left( {x + 90} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 60 = 0\\x + 90 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 60\,\,\,\,\,\,\left( {tm} \right)\\x = - 90\,\,\left( {ktm} \right)\end{array} \right.\end{array}\) Vậy số quyển sách mỗi giờ nhóm dự định sắp xếp là 60 quyển. 3) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \({x^2} - 2x - 1 = 0\). Hãy lập một phương trình bậc hai một ẩn có hai nghiệm là \(\left| {{{\left( {{x_1}} \right)}^3}} \right|\), \(\left| {{{\left( {{x_2}} \right)}^3}} \right|\). Xét phương trình \({x^2} - 2x - 1 = 0\) có \(ac = - 1 < 0\) nên phương trình luôn có hai nghiệm phân biệt trái dấu. Gọi \({x_1},\,\,{x_2}\) là 2 nghiệm phân biệt của phương trình \({x^2} - 2x - 1 = 0\), áp dụng định lí Vi-ét t có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = - 1\end{array} \right.\). Vì hai nghiệm \({x_1},\,\,{x_2}\) trái dấu nên không mất tính tổng quát, ta giả sử \({x_1} < 0 < {x_2}\). Khi đó ta có: \(\begin{array}{l}S = \left| {{{\left( {{x_1}} \right)}^3}} \right| + \left| {{{\left( {{x_2}} \right)}^3}} \right| = - x_1^3 + x_2^3\\\,\,\,\,\, = {\left( {{x_2} - {x_1}} \right)^3} + 3{x_1}{x_2}\left( {{x_2} - {x_1}} \right)\\\,\,\,\,\, = {\left( {{x_2} - {x_1}} \right)^3} - 3\left( {{x_2} - {x_1}} \right)\\P = \left| {{{\left( {{x_1}} \right)}^3}} \right|.\left| {{{\left( {{x_2}} \right)}^3}} \right| = - x_1^3.x_2^3\\\,\,\,\, = - {\left( {{x_1}{x_2}} \right)^3} = - {\left( { - 1} \right)^3} = 1\end{array}\) Ta có: \(\begin{array}{l}{\left( {{x_2} - {x_1}} \right)^2} = {\left( {{x_2} + {x_1}} \right)^2} - 4{x_2}{x_1} = {2^2} - 4.\left( { - 1} \right) = 8\\ \Rightarrow \left| {{x_2} - {x_1}} \right| = \sqrt 8 \\ \Leftrightarrow {x_2} - {x_1} = \sqrt 8 \,\,\left( {Do\,\,{x_2} > {x_1}} \right)\end{array}\) Khi đó ta có: \(S = \left| {{{\left( {{x_1}} \right)}^3}} \right| + \left| {{{\left( {{x_2}} \right)}^3}} \right| = {\left( {\sqrt 8 } \right)^3} - 3\left( {\sqrt 8 } \right) = 8\sqrt 8 - 3\sqrt 8 = 5\sqrt 8 = 10\sqrt 2 \). Vì \({S^2} - 4P = {\left( {10\sqrt 2 } \right)^2} - 4.4 = 184 > 0\) nên \(\left| {{{\left( {{x_1}} \right)}^3}} \right|,\,\,\left| {{{\left( {{x_2}} \right)}^3}} \right|\) là nghiệm của phương trình \({X^2} - 10\sqrt 2 X + 1 = 0\). Vậy \(\left| {{{\left( {{x_1}} \right)}^3}} \right|,\,\,\left| {{{\left( {{x_2}} \right)}^3}} \right|\) là nghiệm của phương trình \({X^2} - 10\sqrt 2 X + 1 = 0\). Câu 4 (1,25 điểm) Cách giải: 1) Rút gọn biểu thức \(P = \left( {\dfrac{{a\sqrt a - 8}}{{a + 2\sqrt a + 4}}} \right)\left( {\dfrac{{a + 5\sqrt a + 6}}{{a - 4}}} \right)\) (với \(a \ge 0\) và \(a \ne 4\)) Với \(a \ge 0,\,\,a \ne 4\) ta có: \(\begin{array}{l}P = \left( {\dfrac{{a\sqrt a - 8}}{{a + 2\sqrt a + 4}}} \right)\left( {\dfrac{{a + 5\sqrt a + 6}}{{a - 4}}} \right)\\P = \left( {\dfrac{{{{\left( {\sqrt a } \right)}^3} - {2^3}}}{{a + 2\sqrt a + 4}}} \right)\left( {\dfrac{{a + 2\sqrt a + 3\sqrt a + 6}}{{\left( {\sqrt a - 2} \right)\left( {\sqrt a + 2} \right)}}} \right)\\P = \dfrac{{\left( {\sqrt a - 2} \right)\left( {a + 2\sqrt a + 4} \right)}}{{a + 2\sqrt a + 4}}.\dfrac{{\sqrt a \left( {\sqrt a + 2} \right) + 3\left( {\sqrt a + 2} \right)}}{{\left( {\sqrt a - 2} \right)\left( {\sqrt a + 2} \right)}}\\P = \left( {\sqrt a - 2} \right).\dfrac{{\left( {\sqrt a + 2} \right)\left( {\sqrt a + 3} \right)}}{{\left( {\sqrt a - 2} \right)\left( {\sqrt a + 2} \right)}}\\P = \sqrt a + 3\end{array}\) Vậy với \(a \ge 0,\,\,a \ne 4\) thì \(P = \sqrt a + 3\). 2) Tìm các số thực \(x\) và \(y\) thỏa mãn \(\left\{ \begin{array}{l}{x^3} = {y^2} + 18\\{y^3} = {x^2} + 18\end{array} \right.\). Xét hệ phương trình \(\left\{ \begin{array}{l}{x^3} = {y^2} + 18\,\,\,\left( 1 \right)\\{y^3} = {x^2} + 18\,\,\,\left( 2 \right)\end{array} \right.\). Trừ vế theo vế của phương trình (1) và (2) ta có: \(\begin{array}{l}\,\,\,\,\,\,\,{x^3} - {y^3} = {y^2} - {x^2}\\ \Leftrightarrow \left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right) = - \left( {x - y} \right)\left( {x + y} \right)\\ \Leftrightarrow \left( {x - y} \right)\left( {{x^2} + xy + {y^2} + x + y} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - y = 0\\{x^2} + xy + {y^2} + x + y = 0\end{array} \right.\end{array}\) TH1: \(x - y = 0 \Leftrightarrow x = y\). Thay vào phương trình (1) ta có: \(\begin{array}{l}\,\,\,\,\,\,{x^3} = {x^2} + 18 \Leftrightarrow {x^3} - {x^2} - 18 = 0\\ \Leftrightarrow {x^3} - 27 - {x^2} + 9 = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - \left( {x - 3} \right)\left( {x + 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {{x^2} + 3x + 9 - x - 3} \right) = 0\\ \Leftrightarrow \left( {x - 3} \right)\left( {{x^2} + 2x + 6} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0 \Leftrightarrow x = 3\\{x^2} + 2x + 6 = 0\end{array} \right.\end{array}\) Xét phương trình \({x^2} + 2x + 6 = 0 \Leftrightarrow {\left( {x + 1} \right)^2} + 5 = 0\) (vô nghiệm do \({\left( {x + 1} \right)^2} + 5 \ge 5 > 0\,\,\,\forall x\)) Với \(x = 3 \Rightarrow y = 3\) \( \Rightarrow \) Hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {3;3} \right)\). TH2: \({x^2} + xy + {y^2} + x + y = 0\). Vì \(\left\{ \begin{array}{l}{x^3} = {y^2} + 18 \ge 18 \Rightarrow x \ge \sqrt[3]{{18}} > 0\\{y^3} = {x^2} + 18 \ge 18 \Rightarrow y \ge \sqrt[3]{{18}} > 0\end{array} \right. \Rightarrow x + y > 0\) Lại có \({x^2} + xy + {y^2} = {x^2} + 2x.\dfrac{1}{2}y + \dfrac{1}{4}{y^2} + \dfrac{3}{4}{y^2} = {\left( {x + \dfrac{1}{2}y} \right)^2} + \dfrac{3}{4}{y^2} \ge 0\,\,\forall x,\,\,y\). Do đó \({x^2} + xy + {y^2} + x + y > 0\,\,\forall x,y\), do đó phương trình \({x^2} + xy + {y^2} + x + y = 0\) vô nghiệm. Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {3;3} \right)\). Câu 5 (2,75 điểm) Cho \(\Delta ABC\) nhọn nội tiếp đường tròn \(\left( O \right)\) có hai đường cao \(BE\) và \(CF\) cắt nhau tại trực tâm \(H,\,\,AB < AC.\) Vẽ đường kính \(AD\) của \(\left( O \right).\) Gọi \(K\) là giao điểm của đường thẳng \(AH\) với đường tròn \(\left( O \right),\,\,\,K \ne A.\) Gọi \(L,\,\,P\) lần lượt là giao điểm của hai đường thẳng \(BC\) và \(EF,\,\,AC\) và \(KD.\)
1) Chứng minh tứ giác \(EHKP\) nội tiếp đường tròn và tâm \(I\) của đường tròn này thuộc đường thẳng \(BC.\) Ta có: \(BE\) là đường cao của \(\Delta ABC\) \( \Rightarrow BE \bot AC\) hay \(\angle BEC = \angle HEC = {90^0}\) \(\angle AKD\) là góc nội tiếp chắn nửa đường tròn \( \Rightarrow AKD = {90^0}\) Xét tứ giác \(EHKP\) ta có: \(\angle HEP + \angle HKP = {90^0} + {90^0} = {180^0}\) Mà hai góc này là hai góc đối diện \( \Rightarrow EHKP\) là tứ giác nội tiếp (đpcm). Có: \(\angle HKP = {90^0}\) là góc nội tiếp chắn cung \(HP\) \( \Rightarrow HP\) là đường kính của đường tròn ngoại tiếp tứ giác \(EHKP.\) \( \Rightarrow \) Tâm \(I\) của đường tròn này là trung điểm của \(HP.\) Gọi \(J\) là giao điểm của \(AK\) và \(BC.\) Ta có: \(\angle HBJ = \angle HAC\) (cùng phụ với \(\angle ACB\)) \(\angle KBC = \angle KAC\) (hai góc nội tiếp cùng chắn cung \(KC\)) Hay \(\angle JBK = \angle HAC\) \( \Rightarrow \angle HBJ = \angle JBK\,\,\left( { = \angle HAC} \right)\) \( \Rightarrow BJ\) là phân giác của \(\angle HBK\) Ta có: \(AH\) là đường cao của \(\Delta ABC\) \( \Rightarrow AH \bot BC = \left\{ J \right\}.\) \( \Rightarrow BJ\) là đường cao của \(\Delta BHK.\) Xét \(\Delta BHK\) ta có: \(BJ\) vừa là đường cao, vừa là đường phân giác từ đỉnh \(B\) của tam giác \( \Rightarrow \Delta BHK\) cân tại \(B\) và \(BJ\) là đường trung tuyến của \(\Delta BHK\) \( \Rightarrow J\) là trung điểm của \(HK.\) Gọi \(I'\) là giao điểm của \(BC\) và \(HP\) Ta có: \(AJ \bot BC = \left\{ J \right\}\) Mà \(KP \bot AH = \left\{ K \right\}\) \( \Rightarrow BC//KP\) hay \(JI'//KP\) Xét \(\Delta HKP\) ta có: \(J\) là trung điểm của \(HK\) (cmt) \(IJ//KP\) (cmt) \( \Rightarrow I'J\) là đường trung bình của \(\Delta HKP.\) \( \Rightarrow I'\) là trung điểm của \(HP\) \( \Rightarrow I \equiv I'\) hay \(I \in BC.\,\,\,\) (đpcm). 2) Gọi \(M\) là trung điểm của đoạn thẳng \(BC.\) Chứng minh \(AH = 2OM.\) Ta có: \(\angle ABD = \angle ACD = {90^0}\) (hai góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \left\{ \begin{array}{l}AB \bot BD\\AC \bot CD\end{array} \right.\) Mà \(\left\{ \begin{array}{l}AB \bot EF\,\,\left( {gt} \right)\\BE \bot AC\,\,\left( {gt} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}CF//BD\\BE//CD\end{array} \right.\) (từ vuông góc đến song song) Hay \(\left\{ \begin{array}{l}BH//CD\\CH//BD\end{array} \right.\)\( \Rightarrow BDCH\) là hình bình hành (dhnb) \( \Rightarrow BC\) cắt \(HD\) tại trung điểm của mỗi đường Lại có \(M\) là trung điểm của \(BC\) (gt) \( \Rightarrow M\) cũng là trung điểm của \(HD.\) Xét \(\Delta AHD\) ta có: \(O,\,\,M\) lần lượt là trung điểm của \(AD,\,\,HD\) \( \Rightarrow OM\) là đường trung bình của \(\Delta AHD\) (định nghĩa) \( \Rightarrow \left\{ \begin{array}{l}OM//AH\\OM = \dfrac{1}{2}AH\end{array} \right. \Rightarrow AH = 2OM\,\,\,\left( {dpcm} \right).\) 3) Gọi \(T\) là giao điểm của đường tròn \(\left( O \right)\) với đường tròn ngoại tiếp \(\Delta EFK,\,\,\,T \ne K.\)Chứng minh rằng ba điểm \(L,\,\,K,\,\,T\) thẳng hàng.
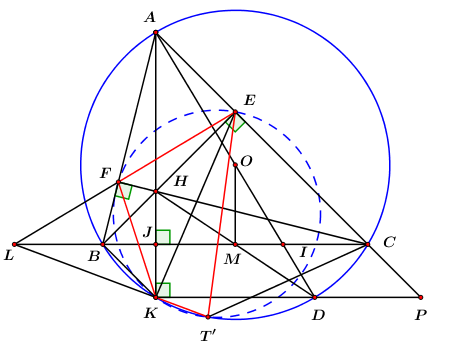
Gọi \(T'\) là giao điểm của tia \(LK\) với đường tròn \(\left( O \right)\) Xét tứ giác \(BFEC\) ta có: \(\angle BFC = \angle BEC = {90^0}\) Mà đỉnh \(F,\,\,E\) là các đỉnh kề nhau \( \Rightarrow BFEC\) là tứ giác nội tiếp. (dhnb) \( \Rightarrow \angle LFB = \angle LCE\) (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện) Xét \(\Delta LFB\) và \(LCE\) ta có: \(\begin{array}{l}\angle L\,\,\,chung\\\angle LFB = \angle LCE\,\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta LFB \sim \Delta LCE\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{LF}}{{LC}} = \dfrac{{LB}}{{LE}} \Rightarrow LE.LF = LB.LC\end{array}\) Ta có tứ giác \(BCT'K\) nội tiếp đường tròn \(\left( O \right)\) \( \Rightarrow \angle LKB = \angle LCT'\) (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện) Xét \(\Delta LBK\) và \(\Delta LCT'\) ta có: \(\begin{array}{l}\angle L\,\,\,chung\\\angle LKB = \angle LCT'\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta LBK \sim \Delta LT'C\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{LB}}{{LT'}} = \dfrac{{LK}}{{LC}} \Leftrightarrow LB.LC = LK.LT'\\ \Rightarrow LE.LF = LK.LT'\,\,\,\left( { = LB.LC} \right)\\ \Rightarrow \dfrac{{LF}}{{LT'}} = \dfrac{{LK}}{{LE}}\end{array}\) Xét \(\Delta LFK\) và \(\Delta LT'E\) ta có: \(\begin{array}{l}\angle ELT'\,\,\,chung\\\dfrac{{LF}}{{LT'}} = \dfrac{{LK}}{{LE}}\\ \Rightarrow \Delta LFK \sim \Delta LT'E\,\,\,\left( {c - g - c} \right)\end{array}\) \( \Rightarrow \angle LKF = \angle LET'\) (hai góc tương ứng) \( \Rightarrow EFKT'\) là tứ giác nội tiếp (Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối diện). \( \Rightarrow T'\) thuộc đường tròn ngoại tiếp tam giác \(EFK.\) \( \Rightarrow T \equiv T' \Rightarrow L,\,\,K,\,\,T\) thẳng hàng. (đpcm) Câu 6 (0,5 điểm) Cách giải: Cho ba số thực dương \(a,\,\,b,\,\,c\) thỏa mãn \(abc = 1\). Chứng minh rằng \({\left( {{a^2} + {b^2} + {c^2}} \right)^3} \ge 9\left( {a + b + c} \right)\). Ta có: \({a^2} + {b^2} + {c^2} = {\left( {a + b + c} \right)^2} - 2\left( {ab + bc + ca} \right)\). Mà \(\left\{ \begin{array}{l}2ab \le {a^2} + {b^2}\\2bc \le {b^2} + {c^2}\\2ca \le {c^2} + {a^2}\end{array} \right. \Rightarrow 2\left( {ab + bc + ca} \right) \le 2\left( {{a^2} + {b^2} + {c^2}} \right)\) \(\begin{array}{l} \Rightarrow {a^2} + {b^2} + {c^2} \ge {\left( {a + b + c} \right)^2} - 2\left( {{a^2} + {b^2} + {c^2}} \right)\\ \Leftrightarrow 3\left( {{a^2} + {b^2} + {c^2}} \right) \ge {\left( {a + b + c} \right)^2}\\ \Leftrightarrow \left( {{a^2} + {b^2} + {c^2}} \right) \ge \dfrac{1}{3}{\left( {a + b + c} \right)^2}\\ \Leftrightarrow {\left( {{a^2} + {b^2} + {c^2}} \right)^3} \ge \dfrac{1}{{27}}{\left( {a + b + c} \right)^6}\end{array}\) Ta cần chứng minh \(\begin{array}{l}\dfrac{1}{{27}}{\left( {a + b + c} \right)^6} \ge 9\left( {a + b + c} \right)\\ \Leftrightarrow {\left( {a + b + c} \right)^6} \ge 243\left( {a + b + c} \right)\\ \Leftrightarrow \left( {a + b + c} \right)\left[ {{{\left( {a + b + c} \right)}^5} - 243} \right] \ge 0\end{array}\) Vì \(a,\,\,b,\,\,c > 0 \Rightarrow a + b + c > 0\). Do đó ta cần chứng minh \({\left( {a + b + c} \right)^5} - 243 \ge 0 \Leftrightarrow {\left( {a + b + c} \right)^5} \ge 243 \Leftrightarrow a + b + c \ge 3\). Áp dụng BĐT Cô-si ta có: \(a + b + c \ge 3\sqrt[3]{{abc}} = 3\). Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a = b = c\\abc = 1\end{array} \right. \Leftrightarrow a = b = c = 1\). Vậy ta có điều phải chứng minh.
|