Đề thi vào 10 môn Toán Bình Dương năm 2019

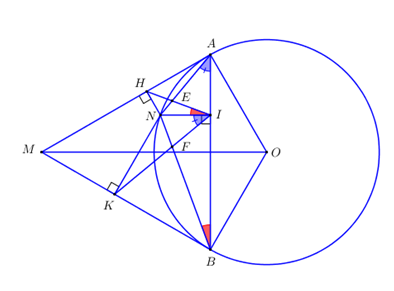
Đề bài

Câu 1 (2 điểm) Giải các phương trình, hệ phương trình sau:

\(1)\,\,{x^2} - 7x + 10 = 0 &  &  & 2)\,\,\,{\left( {{x^2} + 2x} \right)^2} - 6{x^2} - 12x + 9 = 0 &  & 3)\,\,\left\{ \begin{array}{l}4x - y = 7\\5x + y = 2\end{array} \right.\)

Câu 2 (1,5 điểm) Cho parabol \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\)  và đường thẳng \(\left( d \right):\,\,y = x + m - 1\) (m là tham số)

1) Vẽ đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\)

2) Gọi \(A\left( {{x_A};\,\,{y_A}} \right),\,\,B\left( {{x_B};\,\,{y_B}} \right)\) là hai giao điểm phân biệt của \(\left( d \right)\) và \(\left( P \right).\) Tìm tất cả các giá trị của tham số \(m\) để \({x_A} > 0,\,\,\,{x_B} > 0.\)

Câu 3 (1,5 điểm) Cho phương trình:\({x^2} + ax + b + 2 = 0\) (a,   b là tham số)

Tìm các giá trị của tham số \(a,\,\,b\) để phương trình trên có hai nghiệm phân biệt \({x_1},\,\,{x_2}\) thỏa mãn điều kiện:\(\left\{ \begin{array}{l}{x_1} - {x_2} = 4\\x_1^3 - x_2^3 = 28\end{array} \right..\)

Câu 4 (1,5 điểm)  Một tổ công nhân theo kế hoạch phải làm 140 sản phẩm trong một thời gian nhất định. Nhưng khi thực hiện năng suất của tổ đã vượt năng suất dự định là 4 sản phẩm mỗi ngày. Do đố tổ đã hoàn thành công việc sớm hơn dự định 4 ngày. Hỏi thực tế mỗi ngày tổ đã làm được bao nhiêu sản phẩm.

Câu 5 (3,5 điểm)  Cho đường tròn \(\left( {O;\,\,R} \right).\) Từ một điểm \(M\) ở ngoài đường tròn \(\left( {O;\,\,R} \right)\) sao cho \(OM = 2R,\) vẽ hai tiếp tuyến \(MA,\,\,MB\) với \(\left( O \right),\) (\(A,\,\,B\) là hai tiếp điểm). Lấy một điểm \(N\) tùy ý trên cung nhỏ \(AB.\) Gọi \(I,\,\,H,\,\,K\) lần lượt là hình chiếu vuông góc của \(N\) trên \(AB,\,\,AM,\,\,BM.\)  

1) Tính diện tích tứ giác \(MAOB\) theo \(R\).

2) Chứng minh \(\angle NIH = \angle NBA\).

3) Gọi \(E\) là giao điểm của \(AN\) và \(IH\), \(F\) là giao điểm của \(BN\) và \(IK\). Chứng minh tứ giác \(IENF\) nội tiếp được trong đường tròn.

4) Giả sử \(O,\,\,N,\,\,M\)thẳng hàng. Chứng minh \(N{A^2} + N{B^2} = 2{R^2}.\)

Lời giải chi tiết

Phương pháp:

1) Sử dụng biệt thức \(\Delta \) để giải phương trình bậc hai hoặc đưa phương trình về dạng tích.

2) Đặt ẩn phụ \(t = {x^2} + 2x\), đưa phương trình về dạng phương trình bậc hai.

3) Giải hệ phương trình bằng phương pháp thế hoặc cộng đại số.

Cách giải:

\(1)\,\,{x^2} - 7x + 10 = 0\)

Ta có: \(\Delta  = {b^2} - 4ac = {7^2} - 4.10 = 9 > 0\)

\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - b + \sqrt \Delta  }}{{2a}} = \dfrac{{7 + \sqrt 9 }}{{2.1}} = 5\\{x_2} = \dfrac{{ - b - \sqrt \Delta  }}{{2a}} = \dfrac{{7 - \sqrt 9 }}{{2.1}} = 2\end{array} \right..\)

Vậy phương trình có hai nghiệm phân biệt \({x_1} = 5;\,\,{x_2} = 2.\)

\(\begin{array}{l}2)\,\,{\left( {{x^2} + 2x} \right)^2} - 6{x^2} - 12x + 9 = 0\\ \Leftrightarrow {\left( {{x^2} + 2x} \right)^2} - 6\left( {{x^2} + 2x} \right) + 9 = 0\,\,\,\,\left( * \right)\end{array}\)

Đặt \({x^2} + 2x = t.\)  Khi đó ta có phương trình:

\(\begin{array}{l}\left( * \right) \Leftrightarrow {t^2} - 6t + 9 = 0 \Leftrightarrow {\left( {t - 3} \right)^2} = 0 \Leftrightarrow t - 3 = 0 \Leftrightarrow t = 3\\ \Leftrightarrow {x^2} + 2x = 3 \Leftrightarrow {x^2} + 2x - 3 = 0 \Leftrightarrow {x^2} + 3x - x - 3 = 0\\ \Leftrightarrow x\left( {x + 3} \right) - \left( {x + 3} \right) = 0 \Leftrightarrow \left( {x + 3} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 3 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 3\\x = 1\end{array} \right..\end{array}\)

Vậy phương trình đã cho có tập nghiệm: \(S = \left\{ { - 3;\,\,1} \right\}.\)

\(3)\,\,\left\{ \begin{array}{l}4x - y = 7\\5x + y = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9x = 9\\y = 4x - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 4.1 - 7 =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 3\end{array} \right.\)

Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\,\,y} \right) = \left( {1; - 3} \right).\)

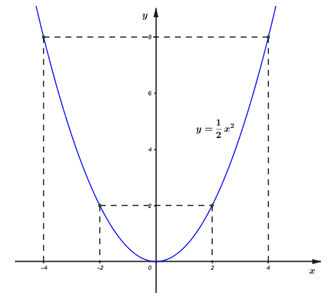
Phương pháp:

1) Lập bảng giá trị, xác định các điểm đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\) đi qua và vẽ đồ thị hàm số.

2) Xét phương trình hoành độ giao điểm của hai đồ thị hàm số \(\left( d \right)\) và \(\left( P \right)\), yêu cầu bài toán tương đương với tìm m để phương trình hoành độ giao điểm có hai nghiệm dương phân biệt.

Cách giải:

1) Vẽ đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\)

Ta có bảng giá trị:

Vậy đồ thị hàm số\(\left( P \right):\,\,\,y = \dfrac{1}{2}{x^2}\) là đường cong đi qua các điểm \(\left( { - 4;\,\,8} \right),\,\,\,\left( { - 2;\,\,2} \right),\,\,\,\left( {0;\,\,0} \right),\,\,\,\left( {2;\,\,2} \right),\,\,\,\left( {4;\,\,8} \right).\)

Đồ thị hàm số \(\left( P \right):\,\,y = \dfrac{1}{2}{x^2}\)

2) Gọi \(A\left( {{x_A};\,\,{y_A}} \right),\,\,B\left( {{x_B};\,\,{y_B}} \right)\) là hai giao điểm phân biệt của \(\left( d \right)\) và \(\left( P \right).\) Tìm tất cả các giá trị của tham số \(m\) để \({x_A} > 0,\,\,\,{x_B} > 0.\)

Ta có phương trình hoành độ giao điểm của hai đồ thị hàm số \(\left( d \right)\) và \(\left( P \right)\)  là:

\(\dfrac{1}{2}{x^2} = x + m - 1 \Leftrightarrow {x^2} - 2x - 2m + 2 = 0\,\,\,\left( * \right)\)

Theo đề bài ta có: \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm \(A\left( {{x_A};\,\,{y_A}} \right),\,\,B\left( {{x_B};\,\,{y_B}} \right)\) phân biệt

\( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0\)

\( \Leftrightarrow 1 - \left( { - 2m + 2} \right) > 0 \Leftrightarrow 1 + 2m - 2 > 0 \Leftrightarrow 2m > 1 \Leftrightarrow m > \dfrac{1}{2}.\)

Vậy với \(m > \dfrac{1}{2}\) thì phương trình \(\left( * \right)\) có hai nghiệm \({x_A},\,\,{x_B}\) phân biệt.

Áp dụng hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_A} + {x_B} = 2\\{x_A}{x_B} =  - 2m + 2\end{array} \right.\)

Theo đề bài ta có: \(\left\{ \begin{array}{l}{x_A} > 0\\{x_B} > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_B} > 0\\{x_A}.{x_B} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 > 0\,\,\forall m\\ - 2m + 2 > 0\end{array} \right. \Leftrightarrow  - 2m >  - 2 \Leftrightarrow m < 1.\)

Kết hợp các điều kiện của \(m\)  ta được: \(\dfrac{1}{2} < m < 1.\)

Vậy \(\dfrac{1}{2} < m < 1\) thỏa mãn bài toán.

Chú ý: Sau khi làm xong phải kết hợp lại các điều kiện của m trước khi đưa ra kết luận cuối cùng.

Phương pháp:

+) Tìm điều kiện để phương trình có hai nghiệm phân biệt \(\left( {\Delta  > 0} \right)\).

+) Áp dụng định lí Vi-ét.

+) Sử dụng các biến đổi \(x_1^3 - x_2^3 = {\left( {{x_1} - {x_2}} \right)^3} + 3{x_1}{x_2}\left( {{x_1} - {x_2}} \right)\) và \({\left( {{x_1} - {x_2}} \right)^2} = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2}\).

Cách giải:

\({x^2} + ax + b + 2 = 0\).

Ta có \(\Delta  = {a^2} - 4\left( {b + 2} \right) = {a^2} - 4b - 8\).

Để phương trình có 2 nghiệm phân biệt thì \(\Delta  > 0 \Leftrightarrow {a^2} - 4b - 8 > 0\) (*).

Khi đó, áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - a\\{x_1}{x_2} = b + 2\end{array} \right.\).

Theo bài ra ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}{x_1} - {x_2} = 4\\x_1^3 - x_2^3 = 28\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} - {x_2} = 4\\{\left( {{x_1} - {x_2}} \right)^3} + 3{x_1}{x_2}\left( {{x_1} - {x_2}} \right) = 28\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_1} - {x_2} = 4\\{4^3} + 12{x_1}{x_2} = 28\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} - {x_2} = 4\\{x_1}{x_2} =  - 3\end{array} \right.\end{array}\)

Mà \({x_1}{x_2} = b + 2 \Rightarrow b + 2 =  - 3 \Leftrightarrow b =  - 3 - 2 =  - 5\).

Ta có : \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - a\\{x_1} - {x_2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{x_1} = 4 - a\\2{x_2} =  - a - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} = \dfrac{{4 - a}}{2}\\{x_2} = \dfrac{{ - a - 4}}{2}\end{array} \right.\)

\(\begin{array}{l} \Rightarrow {x_1}{x_2} =  - 3 \Leftrightarrow \dfrac{{4 - a}}{2}.\left( {\dfrac{{ - a - 4}}{2}} \right) =  - 3\\ \Leftrightarrow \left( {4 - a} \right)\left( {a + 4} \right) = 12\\ \Leftrightarrow 16 - {a^2} = 12\\ \Leftrightarrow {a^2} = 4 \Leftrightarrow \left[ \begin{array}{l}a = 2\\a =  - 2\end{array} \right..\end{array}\)

Với \({a^2} = 4,\,\,b =  - 5 \Rightarrow {a^2} - 4b - 8 = 4 - 4.\left( { - 5} \right) - 8 = 16 > 0 \Rightarrow \) thỏa mãn điều kiện \(\left( * \right)\).

Vậy có 2 cặp số \(\left( {a;b} \right)\) thỏa mãn yêu cầu bài toán là \(\left( {a;b} \right) = \left( {2; - 5} \right)\) hoặc \(\left( {a;b} \right) = \left( { - 2; - 5} \right)\). 

Chú ý: Khi tìm được cặp số \(\left( {a;b} \right)\) phải đối lại chiếu với điều kiện.

Phương pháp:

Gọi số sản phẩm thực tế mỗi ngày tổ công nhân sản xuất được là \(x\) (sản phẩm) \(\left( {x \in \mathbb{N}*,\,\,x > 4} \right).\)

Dựa vào các giả thiết bài cho để biểu diễn số sản phẩm tổ công nhân sản xuất theo kế hoạch và thời gian tổ hoàn thành sản phẩm theo kế hoạch và theo thực tế.

Lập phương trình và giải phương trình.

Đối chiếu với điều kiện của ẩn rồi kết luận.

Cách giải:

Gọi số sản phẩm thực tế mỗi ngày tổ công nhân sản xuất được là \(x\) (sản phẩm) \(\left( {x \in \mathbb{N}*,\,\,x > 4} \right).\)

\( \Rightarrow \) Thời gian thực tế mà tổ công nhân hoàn thành xong \(140\) sản phẩm là: \(\dfrac{{140}}{x}\) ngày.

Theo kế hoạch mỗi ngày tổ công nhân đó sản xuất được số sản phẩm là: \(x - 4\) (sản phẩm)

\( \Rightarrow \) Thời gian theo kế hoạch mà tổ công nhân hoàn thành xong \(140\) sản phẩm là: \(\dfrac{{140}}{{x - 4}}\) (ngày)

Theo đề bài ta có thời gian thực tế hoàn thành xong sớm hơn so với thời gian dự định là \(4\) ngày nên ta có phương trình:

\(\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{{140}}{{x - 4}} - \dfrac{{140}}{x} = 4\\ \Leftrightarrow 140x - 140\left( {x - 4} \right) = 4x\left( {x - 4} \right)\\ \Leftrightarrow 35x - 35\left( {x - 4} \right) = x\left( {x - 4} \right)\\ \Leftrightarrow 35x - 35x + 140 = {x^2} - 4x\\ \Leftrightarrow {x^2} - 4x - 140 = 0\\ \Leftrightarrow {x^2} - 14x + 10x - 140 = 0\\ \Leftrightarrow x\left( {x - 14} \right) + 10\left( {x - 14} \right) = 0\\ \Leftrightarrow \left( {x + 10} \right)\left( {x - 14} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 10 = 0\\x - 14 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 10\,\,\,\,\left( {ktm} \right)\\x = 14\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy thực tế mỗi ngày tổ công nhân đã làm được \(14\) sản phẩm.

Chú ý: Nếu bạn học sinh nào gọi số sản phẩm tổ công nhân dự định làm trong một ngày thì sau khi giải phương trình, ta cần tìm số sản phẩm tổ công nhân làm được theo kế hoạch rồi mới kết luận.

Phương pháp:

1) Áp dụng định lí Pytago tính cạnh \(AM\).

    Tính diện tích tam giác \(OAM\).

    Chứng minh \(\Delta OAM = \Delta OBM \Rightarrow {S_{MAOB}} = 2{S_{\Delta OAM}}\).

2) Sử dụng các định lí: Trong 1 đường tròn, hai góc nội tiếp cùng chắn cung 1 cung thì bằng nhau và góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn 1 cung thì bằng nhau.

3) Chứng minh \(\angle EIF + \angle ENF = {180^0}\).

4) Khi \(O,\,\,M,\,\,N\) thẳng hàng, ta chứng minh được \(N\) là trung điểm của \(OM.\)

Khi đó ta chứng minh \(NA = NB = R\) và suy ra điều phải chứng minh.

Cách giải:

1) Tính diện tích tứ giác \(MAOB\) theo \(R\).

Xét tam giác \(OAM\) và tam giác \(OBM\) ta có:

\(\begin{array}{l}OA = OB\,\,\left( { = R} \right);\\OM\,\,chung;\end{array}\)

\(MA = MB\)  (Tính chất 2 tiếp tuyến cắt nhau) ;

\(\begin{array}{l} \Rightarrow \Delta OAM = \Delta OBM\,\,\left( {c.c.c} \right) \Rightarrow {S_{\Delta OAM}} = {S_{\Delta OBM}}\\ \Rightarrow {S_{MAOB}} = {S_{\Delta OAM}} + {S_{\Delta OBM}} = 2{S_{\Delta OAM}}.\end{array}\)

Áp dụng định lí Pytago trong tam giác vuông \(OAM\) ta có:

\(A{M^2} = O{M^2} - O{A^2} = {\left( {2R} \right)^2} - {R^2}