Đề thi vào 10 môn Toán Bến Tre năm 2020Tải vềCâu 1: a) Trục căn thức ở mẫu của biểu thức
Lựa chọn câu để xem lời giải nhanh hơn
Tải về
Đề bài Câu 1: a) Trục căn thức ở mẫu của biểu thức \(\dfrac{{18}}{{\sqrt 3 }}\) b) Tìm \(x\) biết \(\sqrt {4x} + \sqrt {9x} = 15\) Câu 2: Cho hàm số bậc nhất \(y = \left( {7 - \sqrt {18} } \right)x + 2020\) a) Hàm số trên đồng biến hay nghịch biến trên \(R\)? Vì sao? b) Tính giá trị của \(y\) khi \(x = 7 + \sqrt {18} \) Câu 3: Cho hàm số \(y = 2{x^2}\) có đồ thị \(\left( P \right)\) a) Vẽ \(\left( P \right)\) b) Tìm tọa độ của các điểm thuộc \(\left( P \right)\) có tung độ bằng \(2.\) Câu 4: a) Giải phương trình: \({x^2} + 5x - 7 = 0\) b) Giải hệ phương trình \(\left\{ \begin{array}{l}7x - y = 18\\2x + y = 9\end{array} \right.\) c) Tìm các giá trị của tham số \(m\) để phương trình \({x^2} - 2\left( {m + 5} \right)x + {m^2} + 3m - 6 = 0\) có hai nghiệm phân biệt. Câu 5: Với giá trị nào của tham số \(m\) thì đồ thị của hai hàm số \(y = x + \left( {5 + m} \right)\) và \(y = 2x + \left( {7 - m} \right)\) cắt nhau tại một điểm nằm trên trục hoành. Câu 6: Cho tam giác ABC vuông tại B có đường cao BH (\(H \in AC\)), biết \(AB = 6cm,AC = 10cm\). Tính độ dài các đoạn thẳng \(BC,BH\). Câu 7: Trên đường tròn (O) lấy hai điểm A, B sao cho \(\angle AOB = {65^0}\) và điểm C như hình vẽ. Tính số đo cung \(AmB,ACB\) và số đo \(\angle ACB\). Câu 8: Cho tam giác nhọn ABC nội tiếp đường tròn (O) và có các đường cao BE, CF cắt nhau tại H (\(E \in AC,F \in AB\)) a) Chứng minh tứ giác AEHF nội tiếp. b) Chứng minh \(AH \bot BC\). c) Gọi \(P,G\) là hai giao điểm của đường thẳng \(EF\) và đường tròn \(\left( O \right)\) sao cho điểm \(E\) nằm giữa điểm P và điểm F. Chứng minh \(AO\) là đường trung trực của đoạn thẳng \(PG\). Lời giải Câu 1 (1 điểm) Cách giải: a) Trục căn thức ở mẫu của biểu thức \(\dfrac{{18}}{{\sqrt 3 }}\) Ta có: \(\dfrac{{18}}{{\sqrt 3 }} = \dfrac{{18\sqrt 3 }}{{\sqrt 3 .\sqrt 3 }} = \dfrac{{18\sqrt 3 }}{3} = 6\sqrt 3 \) b) Tìm \(x\) biết \(\sqrt {4x} + \sqrt {9x} = 15\) Điều kiện: \(x \ge 0\) Ta có: \(\begin{array}{l}\sqrt {4x} + \sqrt {9x} = 15\\ \Leftrightarrow \sqrt 4 .\sqrt x + \sqrt 9 .\sqrt x = 15\\ \Leftrightarrow 2\sqrt x + 3\sqrt x = 15\\ \Leftrightarrow 5\sqrt x = 15\\ \Leftrightarrow \sqrt x = 3\\ \Leftrightarrow x = 9\left( {tm} \right)\end{array}\) Vậy phương trình đã cho có nghiệm \(x = 9.\) Câu 2 (1 điểm) Cách giải: Cho hàm số bậc nhất \(y = \left( {7 - \sqrt {18} } \right)x + 2020\) a) Hàm số trên đồng biến hay nghịch biến trên \(R\)? Vì sao? Hàm số \(y = \left( {7 - \sqrt {18} } \right)x + 2020\) có \(a = 7 - \sqrt {18} \) Ta có: \(7 = \sqrt {49} > \sqrt {18} \Leftrightarrow 7 - \sqrt {18} > 0 \Leftrightarrow a > 0\) nên hàm số đã cho đồng biến trên \(R.\) b) Tính giá trị của \(y\) khi \(x = 7 + \sqrt {18} \) Thay \(x = 7 + \sqrt {18} \) vào hàm số \(y = \left( {7 - \sqrt {18} } \right)x + 2020\) ta được: \(y = \left( {7 - \sqrt {18} } \right)\left( {7 + \sqrt {18} } \right) + 2020\) \( = {7^2} - 18 + 2020 = 2051\) Vậy với \(x = 7 + \sqrt {18} \) thì \(y = 2051\). Câu 3 (1 điểm) Cách giải: Cho hàm số \(y = 2{x^2}\) có đồ thị \(\left( P \right)\) a) Vẽ \(\left( P \right)\) Bảng giá trị:
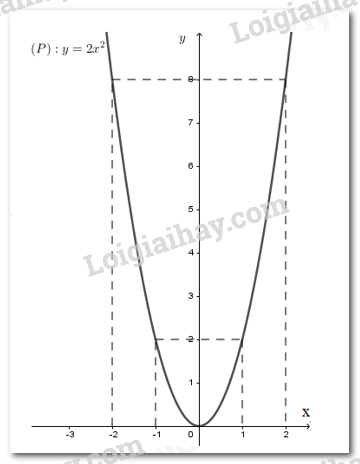
Đồ thị hàm số \(y = 2{x^2}\) là parabol \(\left( P \right)\) đi qua các điểm \(\left( { - 2;8} \right),\left( { - 1;2} \right),\left( {0;0} \right),\left( {1;2} \right),\left( {2;8} \right)\) Hình vẽ:
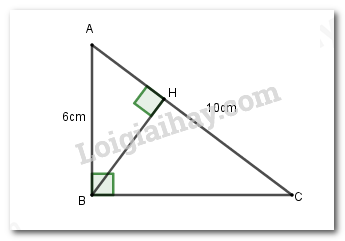
b) Tìm tọa độ của các điểm thuộc \(\left( P \right)\) có tung độ bằng \(2.\) Gọi điểm \(N\left( {x;2} \right)\) thuộc \(\left( P \right):y = 2{x^2}\) Ta có: \(2 = 2{x^2} \Leftrightarrow {x^2} = 1 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\) Vậy ta có hai điểm thỏa mãn đề bài là \(\left( {1;2} \right),\left( { - 1;2} \right)\) Câu 4 (2,5 điểm) Cách giải: a) Giải phương trình: \({x^2} + 5x - 7 = 0\) Ta có: \(\Delta = {5^2} - 4.1.\left( { - 7} \right) = 53 > 0\) nên phương trình đã cho có hai nghiệm phân biệt: \(\left[ \begin{array}{l}x = \dfrac{{ - 5 + \sqrt {53} }}{2}\\x = \dfrac{{ - 5 - \sqrt {53} }}{2}\end{array} \right.\) Vậy phương trình đã cho có hai nghiệm phân biệt \(x = \dfrac{{ - 5 + \sqrt {53} }}{2};x = \dfrac{{ - 5 - \sqrt {53} }}{2}\) b) Giải hệ phương trình \(\left\{ \begin{array}{l}7x - y = 18\\2x + y = 9\end{array} \right.\) Ta có: \(\left\{ \begin{array}{l}7x - y = 18\\2x + y = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9x = 27\\2x + y = 9\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 3\\2.3 + y = 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 3\end{array} \right.\) Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {3;3} \right)\) c) Tìm các giá trị của tham số \(m\) để phương trình \({x^2} - 2\left( {m + 5} \right)x + {m^2} + 3m - 6 = 0\) có hai nghiệm phân biệt. Xét phương trình \({x^2} - 2\left( {m + 5} \right)x + {m^2} + 3m - 6 = 0\) có \(a = 1;b' = - \left( {m + 5} \right);c = {m^2} + 3m - 6\) Ta có: \(\Delta ' = {\left[ { - \left( {m + 5} \right)} \right]^2} - \left( {{m^2} + 3m - 6} \right)\) \(\begin{array}{l} = {m^2} + 10m + 25 - {m^2} - 3m + 6\\ = 7m + 31\end{array}\) Để phương trình đã cho có hai nghiệm phân biệt thì \(\left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 \ne 0\left( {ld} \right)\\7m + 31 > 0\end{array} \right. \Leftrightarrow 7m > - 31 \Leftrightarrow m > \dfrac{{ - 31}}{7}\) Vậy với \(m > - \dfrac{{31}}{7}\) thì phương trình đã cho có hai nghiệm phân biệt. Câu 5 (1 điểm) Cách giải: Với giá trị nào của tham số \(m\) thì đồ thị của hai hàm số \(y = x + \left( {5 + m} \right)\) và \(y = 2x + \left( {7 - m} \right)\) cắt nhau tại một điểm nằm trên trục hoành. Xét đường thẳng \(\left( d \right):y = x + \left( {5 + m} \right)\) có \(a = 1\) và đường thẳng \(\left( {d'} \right):y = 2x + \left( {7 - m} \right)\) có \(a' = 2\) Vì \(a \ne a'\left( {1 \ne 2} \right)\) nên hai đường thẳng \(\left( d \right)\) và \(\left( {d'} \right)\) cắt nhau. Gọi \(M\left( {x;y} \right)\) là giao điểm của hai đường thẳng \(\left( d \right)\) và \(\left( {d'} \right)\) Vì \(M\left( {x;y} \right)\) thuộc trục hoành nên \(M\left( {x;0} \right)\) Lại có \(M\left( {x;0} \right)\) thuộc \(\left( d \right):y = x + \left( {5 + m} \right)\) nên ta có \(x + 5 + m = 0 \Leftrightarrow x = - 5 - m\) Và \(M\left( {x;0} \right)\) thuộc \(\left( {d'} \right):y = 2x + \left( {7 - m} \right)\) nên ta có \(2x + 7 - m = 0 \Leftrightarrow x = \dfrac{{m - 7}}{2}\) \(\begin{array}{l} \Rightarrow - 5 - m = \dfrac{{m - 7}}{2}\\ \Leftrightarrow m - 7 = - 2m - 10\\ \Leftrightarrow 3m = - 3\\ \Leftrightarrow m = - 1\end{array}\) Vậy \(m = - 1\) là giá trị cần tìm. Câu 6 (0,75 điểm) Cách giải: Cho tam giác ABC vuông tại B có đường cao BH (\(H \in AC\)), biết \(AB = 6cm,AC = 10cm\). Tính độ dài các đoạn thẳng \(BC,BH\).
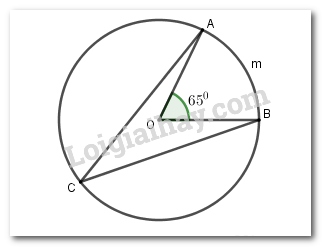
Xét tam giác \(ABC\) vuông tại \(B\), theo định lý Pytago ta có: \(\begin{array}{l}A{C^2} = A{B^2} + B{C^2}\\ \Leftrightarrow B{C^2} = A{C^2} - A{B^2} = {10^2} - {6^2} = 64\\ \Rightarrow BC = 8cm\end{array}\) Xét tam giác \(ABC\) vuông tại \(B\) có chiều cao \(BH\), theo hệ thức lượng trong tam giác vuông ta có: \(BH.AC = AB.BC\) \( \Leftrightarrow BH = \dfrac{{AB.BC}}{{AC}} = \dfrac{{6.8}}{{10}} = 4,8cm\) Vậy \(BC = 8cm,BH = 4,8cm\). Câu 7 (0,75 điểm) Cách giải: Trên đường tròn (O) lấy hai điểm A, B sao cho \(\angle AOB = {65^0}\) và điểm C như hình vẽ. Tính số đo cung \(AmB,ACB\) và số đo \(\angle ACB\).
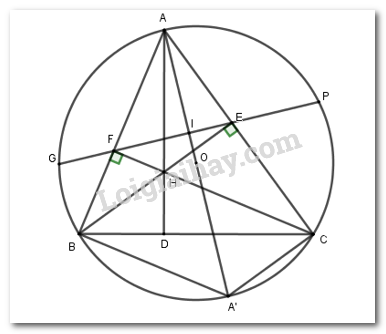
Ta có \(\angle AOB\) là góc ở tâm chắn cung \(AmB\) nên \(sd\,cung\,AmB = \angle AOB = {65^0}\) (tính chất) Lại có \(\begin{array}{l}sdACB + sdAmB = {360^0}\\ \Rightarrow sdACB = {360^0} - sdAmB\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {65^0}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {295^0}\end{array}\) \(\angle ACB\) là góc nội tiếp chắn cung \(AmB\) nên \(\angle ACB = \dfrac{1}{2}sd\,cung\,AmB = \dfrac{1}{2}{.65^0} = 32,{5^0}\) Vậy \(sd\,cung\,AmB = {65^0};\,\,\,sd\,cung\,ACB = {295^0}\) và \(\angle ACB = 32,{5^0}.\) Câu 8 (2,0 điểm) Cách giải: Cho tam giác nhọn ABC nội tiếp đường tròn (O) và có các đường cao BE, CF cắt nhau tại H (\(E \in AC,F \in AB\))
a) Chứng minh tứ giác AEHF nội tiếp. Ta có: \(CF \bot AB \Rightarrow \angle AFC = {90^0}\) \(BE \bot AC \Rightarrow \angle AEB = {90^0}\) Tứ giác AFHE có \(\angle AFH + \angle AEH = {90^0} + {90^0} = {180^0}\) nên là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\)) (đpcm). b) Chứng minh \(AH \bot BC\). Kéo dài \(AH\) cắt BC tại D. Do \(BE,CF\) là các đường cao trong tam giác và \(BE \cap CF = \left\{ H \right\}\) nên \(H\) là trực tâm của \(\Delta ABC\) \( \Rightarrow AD\) là đường cao trong \(\Delta ABC\) \( \Rightarrow AD \bot BC\). \( \Rightarrow AH \bot BC\) (đpcm) c) Gọi \(P,G\) là hai giao điểm của đường thẳng \(EF\) và đường tròn \(\left( O \right)\) sao cho điểm \(E\) nằm giữa điểm P và điểm F. Chứng minh \(AO\) là đường trung trực của đoạn thẳng \(PG\). Xét tứ giác BFEC có \(\angle BFC = \angle BEC = {90^0}\) nên là tứ giác nội tiếp (hai đỉnh kề nhau cùng nhìn cạnh đối diện các góc bằng nhau) \( \Rightarrow \angle AFE = \angle ACB\) (cùng bù với \(\angle BFE\)) (1) Kẻ đường kính \(AA'\) , gọi \(I\) là giao điểm của \(AO\) và \(PG\). Tứ giác \(BACA'\) nội tiếp nên \(\angle BAA' = \angle BCA'\) (góc nội tiếp cùng chắn cung \(BA'\)) (2) Từ (1) và (2) suy ra \( \Rightarrow \angle AFE + \angle BAA' = \angle ACB + \angle BCA'\) Mà \(\angle ACB + \angle BCA' = \angle A'CA = {90^0}\) (góc nội tiếp chắn nửa đường tròn) Nên \(\angle AFE + \angle BAA' = {90^0}\) hay \(\angle AFI + \angle FAI = {90^0}\) \( \Rightarrow \angle AIF = {90^0}\) \( \Rightarrow AO \bot PG\) tại \(I\) \( \Rightarrow I\) là trung điểm của \(PG\) (đường kính vuông góc với dây thì đi qua trung điểm của dây ấy) \( \Rightarrow AO\) là đường trung trực của \(PG\). (đpcm)
|