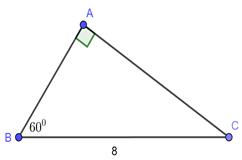
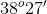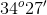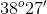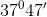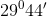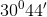Bài tập cơ bản về Một số hệ thức về cạnh và góc trong tam giác vuôngLàm bàiCâu hỏi 1 : Cho tam giác \(ABC\) vuông tại \(A\) có \(\angle B = {60^0}\), cạnh \(BC = 8.\) Tính độ dài cạnh \(AB;AC\).
Đáp án: B Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông: \(\left\{ \begin{array}{l}AB = BC\cos B\\AC = BC\sin B\end{array} \right..\) Lời giải chi tiết:
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AC = BC.sinB = 8.sin{60^0} = 8.\frac{{\sqrt 3 }}{2} = 4\sqrt 3 \) \(AB = BC.cosB = 8.cos{60^0} = 8.\frac{1}{2} = 4\) Chọn B. Câu hỏi 2 : Cho tam giác \(ABC\) vuông tại \(A\), biết \(AB{\rm{ }} = {\rm{ }}8cm,{\rm{ }}AC{\rm{ }} = 15cm.\) Giải tam giác \(ABC\).
Đáp án: B Phương pháp giải: Sử dụng định lý Pitago để tính cạnh BC. Từ tỷ số lượng giác suy ra số đo góc B. Áp dụng tổng hai góc phụ nhau trong tam giác vuông để tính số đo góc C. Lời giải chi tiết: Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {8^2} + {15^2} = 289\)\( \Rightarrow BC = 17\,\,cm.\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(sinB = \frac{{AC}}{{BC}} = \frac{{15}}{{17}} \Rightarrow \angle B \approx {61^0}56'\) Vì \(\Delta ABC\) vuông tại \(A\) ta có: \(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {61^0}56' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {28^0}4'\) Chọn B. Câu hỏi 3 : Cho hình vẽ sau, tính \(x,\,\,y.\)
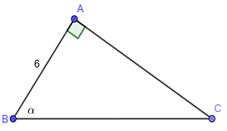
Đáp án: D Phương pháp giải: Sử dụng tỉ số lượng giác của các góc nhọn trong tam giác vuông để làm bài toán. Lời giải chi tiết: Dựa vào hình vẽ ta có: \(\cos \angle MPN = \frac{{MP}}{{NP}} = \frac{6}{{12}} = \frac{1}{2} \Rightarrow x = \angle MPN = {60^0}.\) Xét \(\Delta MPE\) vuông tại \(E\) ta có: \(y = ME = MP.\cos \angle MPE = 6.\cos {60^0} = 3\,\,cm.\) Vậy \(x = {60^0},\,\,\,y = 3\,cm.\) Câu hỏi 4 : Cho tam giác \(ABC\) vuông tại \(A\) có \(AB{\rm{ }} = {\rm{ }}6cm,\angle B = \alpha \), biết \({\rm{tan}}\alpha = \frac{5}{{12}}.\) Hãy tính: \(BC;AC\)
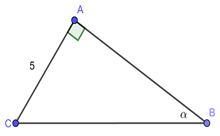
Đáp án: A Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông \(AC = AB.\tan B.\) Sử dụng định lý Pitago để tính độ dài cạnh BC. Lời giải chi tiết: Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AC = AB.tanB = 6.\frac{5}{{12}} = \frac{5}{2} = 2,5\,cm.\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {6^2} + {\left( {2,5} \right)^2} = \frac{{169}}{4}\) \( \Rightarrow BC = \frac{{13}}{2} = 6,5\,\,cm.\) Chọn A. Câu hỏi 5 : Cho tam giác \(ABC\) vuông tại \(A\) có \(AC{\rm{ }} = {\rm{ 5}}cm,\angle B = \alpha ,\) biết \({\rm{cot}}B = 2,4.\) Tính \(AB,\,\,BC.\)
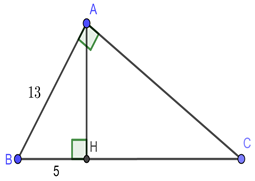
Đáp án: D Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông \(AB = AC\cot B.\) Sử dụng định lý Pitago để tính độ dài cạnh BC. Lời giải chi tiết: Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AB = AC.cotB = 5.2,4 = 12\,\,cm.\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {5^2} + {12^2} = 169\)\( \Rightarrow BC = 13\,\,cm\) Chọn D. Câu hỏi 6 : Cho tam giác \(ABC\) vuông tại \(A\). Kẻ đường cao \(AH.\) Tính \(\sin B;\,\,\sin C\) trong mỗi trường hợp sau: Câu 1: Biết \(AB{\rm{ }} = {\rm{ 13}}cm,BH = 5cm\).
Đáp án: C Phương pháp giải: Áp dụng định lý Pitago để tính độ dài cạnh AH. Áp dụng hệ thức về cạnh và góc trong tam giác vuông: \(\sin B = \frac{{AH}}{{AB}}.\) Áp dụng hệ thức lượng trong tam giác vuông để tính cạnh BC. Từ đó tính: \(\sin C = \frac{{AB}}{{BC}}.\) Lời giải chi tiết: Áp dụng định lý Pitago cho \(\Delta ABH\) vuông tại \(H\) có: \(A{H^2} + B{H^2} = A{B^2}\) \( \Leftrightarrow A{H^2} + {5^2} = {13^2}\) \( \Leftrightarrow A{H^2} = 144 \Rightarrow AH = 12\,cm.\) Xét \(\Delta ABH\) vuông tại \(H\) ta có: \(\sin B = \frac{{AH}}{{AB}} = \frac{{12}}{{13}}\) Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A,\) có đường cao \(AH\) ta có: \(A{B^2} = BH.BC\) \( \Leftrightarrow {13^2} = 5.BC \Rightarrow BC = \frac{{169}}{5}\,\,cm.\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\sin C = \frac{{AB}}{{BC}} = 13:\frac{{169}}{5} = \frac{5}{{13}}\) Chọn C. Câu 2: Biết \(BH{\rm{ }} = {\rm{ 3}}cm,CH = 4cm\)
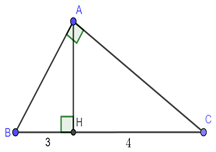
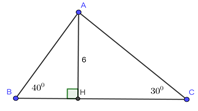
Đáp án: B Phương pháp giải: Sử dụng hệ thức lượng trong tam giác vuông \(A{B^2} = BH.BC\); \(A{C^2} = CH.BC\) Sử dụng hệ thức về cạnh và góc để tính \(\sin B,\,\,\sin C.\) Lời giải chi tiết: Ta có: \(BC = BH + CH = 3 + 4 = 7cm.\) Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A,\) có đường cao \(AH\) ta có: \(A{B^2} = BH.BC\) \( \Leftrightarrow A{B^2} = 3.7\)\( \Rightarrow AB = \sqrt {21} \) \(A{C^2} = CH.BC\)\( \Leftrightarrow A{C^2} = 4.7\)\( \Rightarrow AC = \sqrt {28} \) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\left\{ \begin{array}{l}\sin B = \frac{{AC}}{{BC}} = \frac{{\sqrt {28} }}{7} = \frac{{2\sqrt 7 }}{7}\\\sin C = \frac{{AB}}{{BC}} = \frac{{\sqrt {21} }}{7} = \frac{{\sqrt {21} }}{7}\end{array} \right.\) Chọn B. Câu hỏi 7 : Cho tam giác ABC, \(\angle B = {40^0};\angle C = {30^0}\), đường cao \(AH{\rm{ }} = {\rm{ 6}}cm\). Tính AB, AC và BC.
Đáp án: D Phương pháp giải: Sử dụng tính chất cộng đoạn thẳng. Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông. Lời giải chi tiết: Xét \(\Delta ABH\) vuông tại \(H\) ta có : \(AH = AB.sinB\) \( \Rightarrow AB = \frac{{AH}}{{sinB}} = \frac{6}{{sin{{40}^0}}} \approx 9,33\) \(HB = AH.cotB = 6.cot{40^0} \approx 7,15\) Xét \(\Delta ACH\) vuông tại \(H\) ta có: \(AH = AC.\sin C\) \( \Rightarrow AC = \frac{{AH}}{{\sin C}} = \frac{6}{{sin{{30}^0}}} = 12\) \(HC = AH.cotC = 6.cot{30^0} = 6\sqrt 3 \) Ta có: \(BC = HB + HC \approx 7,15 + 6\sqrt 3 \) Chọn D. Câu hỏi 8 : Cho hình vẽ sau. a) Tính NK b) Tính số đo góc P
Đáp án: C Phương pháp giải: Lời giải chi tiết:
Câu hỏi 9 : Cho hình vẽ sau a) Tính DH b) Tính số đo góc E
Đáp án: A Phương pháp giải: Lời giải chi tiết:
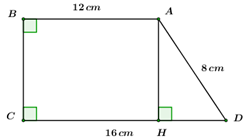
Câu hỏi 10 : Cho hình thang vuông \(ABCD\) có hai đáy \(AB = 12\,cm,\,\,DC = 16\,\,cm,\) cạnh xiên \(AD = 8\,cm.\) Tính các góc và cạnh góc vuông của hình thang.
Đáp án: D Phương pháp giải: Kẻ \(AH \bot CD = \left\{ H \right\},\,\,H \in CD.\) Sử dụng tính chất hình thang vuông, hình chữ nhật; định lý Pitago và hệ thức lượng giác trong tam giác vuông để tính. Lời giải chi tiết: Kẻ \(AH \bot CD = \left\{ H \right\},\,\,H \in CD.\) Có hình thang vuông \(ABCD\) cạnh xiên \(AD \Rightarrow \angle ABC = \angle BCD = {90^o}.\) Dễ thấy \(ABCH\) là hình chữ nhật (có 3 góc vuông) \( \Rightarrow HC = AB = 12\,cm\) \( \Rightarrow HD = DC - HC = 16 - 12 = 4\,\,(cm)\) Áp dụng định lý Pitago cho \(\Delta AHD\) vuông tại \(H\) ta có: \(\begin{array}{l}A{H^2} = A{D^2} - H{D^2} \Rightarrow AH = \sqrt {A{D^2} - H{D^2}} = \sqrt {{8^2} - {4^2}} = 4\sqrt 3 \,\,\left( {cm} \right).\\ \Rightarrow BC = AH \approx 6,93\,\,cm\end{array}\) Xét \(\Delta AHD\) vuông tại \(H\) ta có: \(\cos \angle D = \frac{{HD}}{{AD}} = \frac{1}{2} \Rightarrow \angle D = {60^o}\) \(\begin{array}{l} \Rightarrow \angle DAH = {90^o} - \angle D = {30^o}\\ \Rightarrow \angle BAD = \angle BAH + \angle DAH = {90^o} + {30^o} = {120^o}.\end{array}\)
|