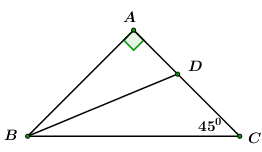
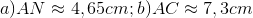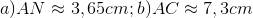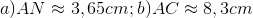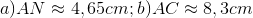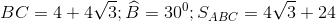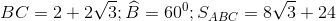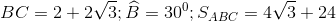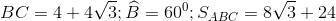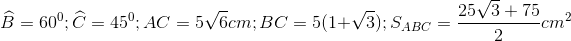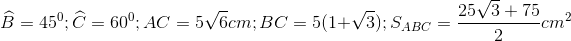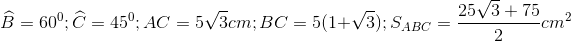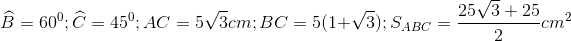20 bài tập vận dụng Một số hệ thức về cạnh và góc trong tam giác vuôngLàm bàiCâu hỏi 1 : Cho tam giác \(ABC\) vuông cân tại \(A\left( {AB = AC = a} \right)\) . Phân giác của góc \(B\) cắt \(AC\) tại \(D\). Tính \(DA;DC\) theo \(a\).
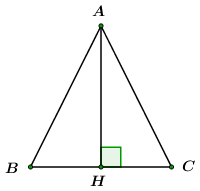
Đáp án: C Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông Sử dụng tính chất tam giác vuông cân và tia phân giác. Lời giải chi tiết: Vì tam giác \(ABC\) vuông cân tại \( \Rightarrow \angle B = \angle C = {45^0}\) Vì \(BD\) là tia phân giác \(B\) \( \Rightarrow \angle ABD = \angle DBC = \frac{1}{2}\angle B = \frac{{{{45}^0}}}{2} = 22,{5^0}\) Xét \(\Delta ABD\) vuông tại \(A\) ta có \(AD = AB.\tan \angle ABD = a.\tan 22,{5^0}\) Ta có: \(AD + DC = AC\)\( \Rightarrow DC = AC - AD = a - a\tan 22,{5^0}\) Chọn C. Câu hỏi 2 : Một tam giác cân có đường cao ứng với đáy đúng bằng độ dài đáy. Tính các góc của tam giác đó.
Đáp án: D Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông. Tính chất tam giác cân. Sử dụng định lý tổng ba góc trong một tam giác. Lời giải chi tiết: Giả sử \(BC = AH = a.\) Vì \(\Delta ABC\) là tam giác cân nên \(AH\) là đường cao đồng thời là đường trung tuyến \( \Rightarrow H\) là trung điểm \(BC\) \( \Rightarrow HB = HC = \frac{{BC}}{2} = \frac{a}{2}\) Xét \(\Delta ABH\) vuông tại \(H\) ta có: \(tan\angle B = \frac{{AH}}{{BH}} = \frac{a}{{\frac{a}{2}}} = 2\) \( \Rightarrow \angle B \approx {63^0}26'\) Vì \(\Delta ABC\) là tam giác cân\( \Rightarrow \angle C = \angle B \approx {63^0}26'\) Ta có \(\angle A + \angle B + \angle C = {180^0}\) (định lý tổng ba góc trong một tam giác) \( \Rightarrow \angle A = {180^0} - 2\angle C \approx {180^0} - {2.63^0}26' \approx {53^0}8'\) Chọn D. Câu hỏi 6 :
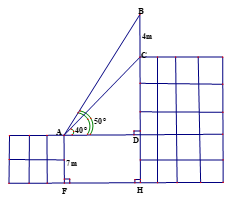
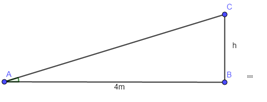
Trên nóc một toàn nhà có một cột ăg-ten thẳng cao 4m. Từ vị trí quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten lần lượt dưới góc 500 và 400 so với phương nằm ngang (như hình vẽ bên) Tính chiều cao CH của tòa nhà (kết quả làm tròn đến chữ số thập phân thứ ba).
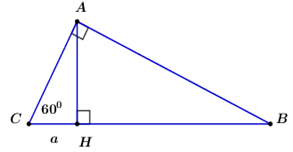
Đáp án: A Phương pháp giải: Lời giải chi tiết: Xét tam giác ABD vuông tại D, ta có: \(\tan BAD=\operatorname{t}\text{an}{{50}^{0}}=\frac{BD}{AD}=\frac{BC+CD}{AD}=\frac{4+CD}{AD}\Rightarrow AD=\frac{4+CD}{\tan {{50}^{0}}}\) (1) Xét tam giác ACD vuông tại D, ta có: \(\tan CAD=\operatorname{t}\text{an 4}{{0}^{0}}=\frac{CD}{AD}\Rightarrow AD=\frac{CD}{\tan {{40}^{0}}}\) (2) Từ (1) và (2) \(\Rightarrow \frac{4+CD}{\tan {{50}^{0}}}=\frac{CD}{\tan {{40}^{0}}}\Leftrightarrow \tan {{40}^{0}}.\left( 4+CD \right)=\tan {{50}^{0}}.CD\Leftrightarrow CD=\frac{4.\tan {{40}^{0}}}{\tan {{50}^{0}}-\tan {{40}^{0}}}=9,518m\) Tứ giác ADHF là hình chữ nhật (vì \(\overset{\hat{\ }}{\mathop{D}}\,=\overset{\hat{\ }}{\mathop{H}}\,=\overset{\hat{\ }}{\mathop{F}}\,={{90}^{0}}\)) \(\Rightarrow AF=DH=7m\) Vậy chiều cao CH của tòa nhà là: \(CH=CD+DH=9,518+7=16,518m\) Câu hỏi 7 : Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) (\(H\) thuộc \(BC\)). Biết \(\angle ACB = {60^0},\,\,CH = a\). Tính độ dài \(AB\) và \(AC\) theo \(a\).
Đáp án: A Phương pháp giải: +) Sử dụng công thức lượng giác để tính các cạnh. Lời giải chi tiết: \(\Delta ACH\) vuông tại \(H\) có: \(\cos C = \frac{{CH}}{{AC}}\,\,\, \Rightarrow AC = \frac{{CH}}{{\cos C}} = \frac{a}{{\cos {{60}^0}}} = \frac{a}{{\frac{1}{2}}} = 2a\) \(\Delta ABC\) có \(AB = AC.\tan C = 2a.\tan {60^0} = 2\sqrt 3 a\) Chọn D. Câu hỏi 8 : Hiện nay tại nước Mỹ quy định cầu thang cho người khuyết tật dùng xe lăn có hệ số góc không quá \(\frac{1}{{12}}\). Để phù hợp với tiêu chuẩn ấy thì chiều cao cầu thang tối đa là bao nhiêu khi biết đáy của cầu thang có độ dài là 4m ?
Đáp án: B Phương pháp giải: Hệ số góc là tan của góc tạo bởi cầu thang với mặt phẳng nằm ngang. Áp dụng công thức tan trong tam giác vuông để tính chiều cao cầu thang Lời giải chi tiết: Ta có hình vẽ minh họa:
Gọi \(h\) là chiều cao tối đa của cầu thang. \(AB = 4\left( m \right)\) là độ dài đáy. Xét tam giác vuông ABC vuông tại B có: \(\tan \left( {\angle BAC} \right) = \frac{{BC}}{{AC}} = \frac{h}{4}\) Mà có hệ số góc là tan của góc tạo bởi cầu thang với mặt phẳng nằm ngang chính là \(\tan \left( {\angle BAC} \right)\) \( \Rightarrow h = 4.\tan \left( {\angle BAC} \right) = 4.\frac{1}{{12}} = \frac{1}{3}\left( m \right)\) Vậy chiều cao tối đa của thang là \(h = \frac{1}{3}\left( m \right)\). Chọn B Câu hỏi 9 : Cho tam giác \(ABC\) vuông tại \(A,\) đường cao \(AH.\) Biết \(AB = 3cm,\,\,AC = 4cm.\) Tính độ dài đường cao \(AH,\) tính \(\cos \angle ACB\) và chu vi tam giác \(ABH.\)
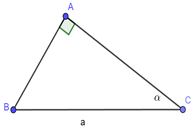
Đáp án: B Phương pháp giải: Sử dụng hệ thức lượng trong tam giác vuông và công thức tỉ số lượng giác để làm bài toán. Lời giải chi tiết: Áp dụng định lý Pitago trong \(\Delta ABC\) vuông tại \(A\) ta có: \(B{C^2} = A{C^2} + A{B^2} = {3^2} + {4^2} = {5^2} \Rightarrow BC = 5\,\,cm.\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(AH.BC = AB.AC \Leftrightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{3.4}}{5} = 2,4cm.\) Ta có: \(\cos \angle ACB = \frac{{AC}}{{BC}} = \frac{4}{5}.\) Chọn B. Câu hỏi 10 : Cho tam giác \(ABC\) vuông tại \(A\); \(BC = a\) không đổi, \(\angle C = \alpha \,\,\,\left( {{0^0} < \alpha < {{90}^0}} \right)\) Câu 1: Lập công thức để tính diện tích tam giác ABC theo \(a\) và .
Đáp án: A Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông. Sử dụng công thức tính diện tích tam giác \({S_{ABC}} = \frac{1}{2}AB.AC.\) Lời giải chi tiết: Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\left\{ \begin{array}{l}AB = BC.\sin \alpha = a.\sin \alpha \\AC = BC.cos\alpha = a.cos\alpha \end{array} \right.\) \({S_{ABC}} = \frac{1}{2}.AB.AC = \frac{1}{2}a.\sin \alpha .a.cos\alpha = \frac{1}{2}{a^2}.\sin \alpha .cos\alpha \) Chọn A. Câu 2: Tìm góc để diện tích tam giác ABC là lớn nhất. Tính giá trị lớn nhất ấy và vẽ hình minh họa.
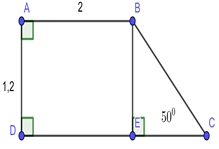
Đáp án: D Phương pháp giải: Sử dụng định lý Pitago. Áp dụng bất đẳng thức Cô-si Lời giải chi tiết: \({S_{ABC}} = \frac{1}{2}.AB.AC \le \frac{1}{2}.\frac{{\left( {A{B^2} + A{C^2}} \right)}}{2} = \frac{1}{4}.\left( {A{B^2} + A{C^2}} \right)\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Rightarrow {S_{ABC}} = \frac{1}{2}.AB.AC \le \frac{1}{4}.\left( {A{B^2} + A{C^2}} \right) = \frac{1}{4}B{C^2} = \frac{1}{4}{a^2}\) Dấu “=” xảy ra \( \Leftrightarrow AC = AB\)\( \Leftrightarrow \Delta ABC\) vuông cân \( \Rightarrow \angle B = \angle C = {45^0}\) hay \(\alpha = {45^0}\). Vậy \({S_{ABCmax}} = \frac{1}{4}{a^2}\) khi \(\alpha = {45^0}.\) Chọn D. Câu hỏi 11 : Cho hình thang \(ABCD\) vuông tại \(A\) và \(D;\)\(\angle C = {50^0}\). Biết \(AB = 2;AD = 1,2\). Tính diện tích hình thang \(ABCD.\)
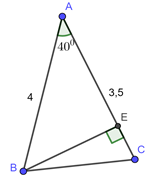
Đáp án: B Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông. Sử dụng tính chất hình chữ nhật. Công thức tính diện tích hình thang vuông: \({S_{ABCD}} = \frac{{\left( {AB + CD} \right).AD}}{2}.\) Lời giải chi tiết: Kẻ \(BE \bot DC,\,\,\,E \in CD.\) Xét tứ giác \(ABED\)có \(\angle A = \angle D = \angle E = {90^0}\) \( \Rightarrow ABED\) là hình chữ nhật \( \Rightarrow \left\{ \begin{array}{l}AB = ED = 2\\AD = BE = 1,2\end{array} \right.\) Xét \(\Delta BCE\) vuông tại \(E\) ta có: \(EC = BE.cot\angle C = 1,2.cot{50^0}\) \( \Rightarrow DC = DE + EC = 2 + 1,2.\cot {50^0}\) \( \Rightarrow {S_{ABCD}} = \frac{{\left( {AB + CD} \right)AD}}{2}\)\( = \frac{{\left( {2 + 2 + 1,2.\cot {{50}^0}} \right).1,2}}{2} \approx 3\,\,\,\,\left( {dvdt} \right).\) Chọn B. Câu hỏi 12 : Cho tam giác \(ABC\)có \(AB = 4;AC = 3,5\). Tính diện tích tam giác \(ABC\) trong hai trường hợp: Câu 1: \(\angle A = {40^0}\)
Đáp án: B Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông. Công thức tính diện tích tam giác. Lời giải chi tiết: \(\angle A = {40^0}\) Kẻ \(BE \bot AC,\,\,E \in AC.\) Xét \(\Delta BEA\) vuông tại \(E\) ta có: \(BE = AB.sin\angle A = 4.sin{40^0}\) \( \Rightarrow {S_{ABC}} = \frac{{BE.AC}}{2} = \frac{{4\sin {{40}^0}.3,5}}{2} \approx 4,5\,\,\,\left( {dvdt} \right).\) Chọn B. Câu 2: \(\angle A = {140^0}\)
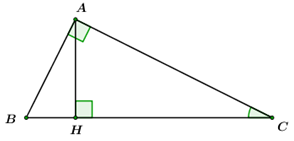
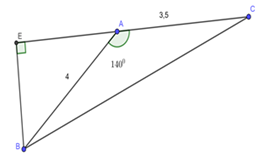
Đáp án: B Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông Sử dụng tính chất hai góc kề bù. Công thức tính diện tích tam giác. Lời giải chi tiết: \(\angle A = {140^0}\) Kẻ \(BE \bot AC\) Xét \(\Delta BEA\) vuông tại \(E\) ta có: Ta có: \(\angle BAE + \angle BAC = {180^0}\) \( \Rightarrow \angle BAE = {180^0} - \angle BAC = {180^0} - {140^0} = {40^0}\) Xét \(\Delta BEA\) vuông tại \(E\) ta có: \(BE = AB.sin\angle BAE = 4.sin{40^0}\) \( \Rightarrow {S_{ABC}} = \frac{{BE.AC}}{2} = \frac{{4\sin {{40}^0}.3,5}}{2} \approx 4,5\,\,\,\left( {dvdt} \right).\) Chọn B. Câu hỏi 13 : Cho tam giác \(ABC\)có góc \(B\) nhọn, các cạnh \(AB = c;AC = b;BC = a\). Chứng minh rằng: \({S_{ABC}} = \frac{1}{2}ac\sin B.\) Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông. Công thức tính diện tich tam giác. Lời giải chi tiết: Xét \(\Delta ABH\) vuông tại \(H\) có: \(sinB = \frac{{AH}}{{AB}}\) \( \Leftrightarrow sinB = \frac{{AH}}{c} \Leftrightarrow AH = csinB\) \( \Rightarrow {S_{ABC}} = \frac{{AH.BC}}{2} = \frac{1}{2}ac\sin B\) (đpcm). Câu hỏi 14 : Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\), biết \(HB = 9;HC = 16\). Tính góc \(B\) và góc \(C.\)
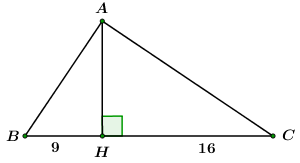
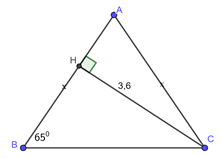
Đáp án: A Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông Từ tỉ số lượng giác suy ra số đo góc Sử dụng hệ thức lượng trong ta giác vuông: \(A{B^2} = BH.BC\); \(A{C^2} = CH.BC\) Lời giải chi tiết: Ta có: \(BC = BH + CH = 9 + 16 = 25\) Áp dụng hệ thức lượng cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(A{B^2} = BH.BC\)\( \Leftrightarrow A{B^2} = 9.25 \Rightarrow AB = 15\) \(A{C^2} = CH.BC\)\( \Leftrightarrow A{C^2} = 16.25 \Rightarrow AC = 20\) Xét \(\Delta ABC\) vuông tại \(A\) ta có \(\sin B = \frac{{AC}}{{BC}} = \frac{{20}}{{25}} = \frac{4}{5} \Rightarrow \angle B \approx {53^0}8'\) \(\sin C = \frac{{AB}}{{BC}} = \frac{{15}}{{25}} = \frac{3}{5} \Rightarrow \angle C \approx {36^0}52'\) Chọn A. Câu hỏi 15 : Cho tam giác \(ABC\) cân tại \(A,\,\,\angle B = {65^0},\) đường cao \(CH = 3,6\). Hãy giải tam giác \(ABC\).
Đáp án: D Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông. Sử dụng tính chất tam giác cân. Sử dụng định lý tổng ba góc trong một tam giác. Lời giải chi tiết: Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow \angle C = \angle B = {65^0}\) Ta có \(\angle A + \angle B + \angle C = {180^0}\)(định lý tổng ba góc trong một tam giác) \( \Rightarrow \angle A = {180^0} - 2\angle C = {180^0} - {2.65^0} = {50^0}\) Xét \(\Delta ACH\) vuông tại \(H\) ta có: \(\sin A = \frac{{CH}}{{AC}}\) \( \Leftrightarrow \sin {50^0} = \frac{{3,6}}{{AC}}\)\( \Rightarrow AC = \frac{{3,6}}{{\sin {{50}^0}}} \approx 4,7\) Vì \(\Delta ABC\) là tam giác cân tại \(A\)\( \Rightarrow AC = AB \approx 4,7\) Xét \(\Delta BCH\) vuông tại \(H\) ta có: \(\sin B = \frac{{CH}}{{BC}} \Leftrightarrow \sin {65^0} = \frac{{3,6}}{{BC}} \Rightarrow BC = \frac{{3,6}}{{\sin {{65}^0}}} \approx 3,97\) Chọn D. Câu hỏi 16 : Cho tam giác \(ABC\) vuông tại \(A\). Giải tam giác vuông trong các trường hợp sau: Câu 1: \(\angle B = {40^0}\)và \(AB{\rm{ }} = {\rm{ 7}}\)
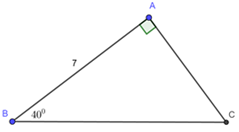
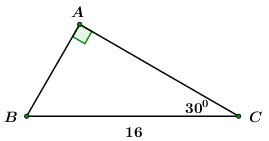
Đáp án: C Phương pháp giải: Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông. Sử dụng tính chất hai góc phụ nhau: Cho \(\angle B + \angle C = {90^0}.\) Khi đó ta có: \(\left\{ \begin{array}{l}\sin B = \cos C\\\cos B = \sin C\end{array} \right..\) Lời giải chi tiết: \(\angle B = {40^0}\) và \(AB = {\rm{7}}{\rm{.}}\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AC = AB.tanB = 7.\tan {40^0} \approx 5,87\) \(AB = BC.\cos B \Rightarrow 7 = BC.\cos {40^0}\)\( \Rightarrow BC = \frac{7}{{\cos {{40}^0}}} \approx 9,14\) Vì \(\Delta ABC\) vuông tại \(A\) ta có: \(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {40^0} + \angle C = {90^0}\)\( \Leftrightarrow \angle C = {50^0}\) Chọn C. Câu 2: \(\angle C = {30^0}\) và \(BC{\rm{ }} = {\rm{ 16}}\)
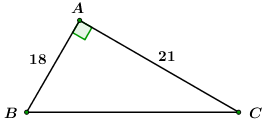
Đáp án: A Phương pháp giải: Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông. Sử dụng tính chất hai góc phụ nhau: Cho \(\angle B + \angle C = {90^0}.\) Khi đó ta có: \(\left\{ \begin{array}{l}\sin B = \cos C\\\cos B = \sin C\end{array} \right..\) Lời giải chi tiết: \(\angle C = {30^0}\) và \(BC = {\rm{16}}{\rm{.}}\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AC = BC.cosC = 16.cos{30^0} = 8\sqrt 3 \) \(AB = BC.\sin C = 16.\sin {30^0} = 8\) Vì \(\Delta ABC\) vuông tại \(A\) ta có: \(\angle B + \angle C = {90^0} \Leftrightarrow \angle B + {30^0} = {90^0}\)\( \Leftrightarrow \angle B = {60^0}\) Chọn A. Câu hỏi 17 : Cho tam giác \(ABC\) vuông tại \(A\). Giải tam giác vuông trong các trường hợp sau: Câu 1: \(AB{\rm{ }} = {\rm{ 18}}cm;AC = 21cm\)
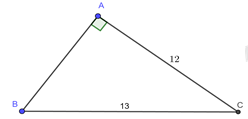
Đáp án: D Phương pháp giải: Sử dụng định lý Pitago cho tam giác ABC vuông tại A để tính độ dài cạnh BC. Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông Sử dụng tính chất hai góc phụ nhau Lời giải chi tiết: \(AB = {\rm{18}}cm;\,\,\,AC = 21cm\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {18^2} + {21^2} = 765\)\( \Rightarrow BC = 3\sqrt {85} \) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(sinB = \frac{{AC}}{{BC}} = \frac{{21}}{{3\sqrt {85} }} \Rightarrow \angle B \approx {49^0}24'\) Vì \(\Delta ABC\) vuông tại \(A\) ta có: \(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {49^0}24' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {40^0}36'\) Chọn D. Câu 2: \(AC{\rm{ }} = {\rm{ 12}}cm;CB = 13cm\)
Đáp án: A Phương pháp giải: Sử dụng định lý Pitago cho tam giác ABC vuông tại A để tính độ dài cạnh BC. Sử dụng công thức liên hệ giữa cạnh và góc trong tam giác vuông Sử dụng tính chất hai góc phụ nhau Lời giải chi tiết: \(AC = {\rm{12}}cm;\,\,\,CB = 13cm\) Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow A{B^2} = {13^2} - {12^2} = 25\)\( \Rightarrow BA = 5\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(sinB = \frac{{AC}}{{BC}} = \frac{{12}}{{13}} \Rightarrow \angle B \approx {67^0}23'\) Vì \(\Delta ABC\) vuông tại \(A\) ta có: \(\angle B + \angle C = {90^0}\)\( \Leftrightarrow {67^0}23' + \angle C = {90^0}\)\( \Leftrightarrow \angle C \approx {22^0}37'\) Chọn A. Câu hỏi 18 : Cho tam giác \(DEF\) có \(DE = 7cm;\angle D = {40^0};\angle F = {58^0}\). Kẻ đường cao \(EI\) của tam giác đó. Hãy tính: (Kết quả làm tròn đến chữ số thập phân thứ 1) Câu 1: Đường cao \(EI\)
Đáp án: A Phương pháp giải: Sử dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông. Lời giải chi tiết: Xét \(\Delta DEI\) vuông tại \(I\) ta có: \(EI = ED.\sin D = 7.\sin {40^0} \approx 4,5\,\,cm.\) Chọn A. Câu 2: Cạnh \(EF\)
Đáp án: B Phương pháp giải: Sử dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông. Lời giải chi tiết: Xét \(\Delta EIF\) vuông tại \(I\) ta có: \(EI = EF.\sin F \Leftrightarrow EF = \frac{{EI}}{{\sin F}} \approx \frac{{4,5}}{{\sin {{58}^0}}} \approx 5,3\,cm.\) Chọn B. Câu hỏi 19 : Cho tam giác nhọn \(ABC\). Gọi \(a,b,c\) lần lượt là độ dài các cạnh \(BC;CA\) và \(AB\). Chứng minh rằng: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}}.\) Phương pháp giải: Áp dụng hệ thức về cạnh và góc trong tam giác vuông. Sử dụng công thức tính diện tích tam giác. Lời giải chi tiết: Xét \(\Delta ABH\) vuông tại \(H\) ta có: \(sinB = \frac{{AH}}{{AB}} \Leftrightarrow sinB = \frac{{AH}}{c}\)\( \Leftrightarrow AH = csinB\) \( \Rightarrow {S_{ABC}} = \frac{{AH.BC}}{2} = \frac{1}{2}ac\sin B\) Chứng minh tương tự ta được: \(\left\{ \begin{array}{l}{S_{ABC}} = \frac{1}{2}ab\sin C\\{S_{ABC}} = \frac{1}{2}bc\sin A\end{array} \right..\) \( \Rightarrow \frac{1}{2}ab\sin C = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B\) (đpcm). Câu hỏi 20 : Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Đặt \(AB = c;AC = b;BC = a\). Chứng minh rằng: a) \(AH = a\sin B\cos B\) b) \(BH = a{\cos ^2}B\) Phương pháp giải: a) Áp dụng hệ thức về cạnh và góc trong tam giác vuông. Sử dụng hệ thức lượng trong tam giác vuông \(AH.BC = AB.AC\) b) Áp dụng hệ thức về cạnh và góc trong tam giác vuông. Sử dụng hệ thức lượng trong tam giác vuông \(A{B^2} = BH.BC\) Lời giải chi tiết: a) \(AH = a\sin B.\sin C\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\begin{array}{l}AB = BC.\sin C = a\sin C\\AC = BC.\sin B = a\sin B\end{array}\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \(AH.BC = AB.AC\)\( \Leftrightarrow AH.a = a\sin B.a\sin C\)\( \Leftrightarrow AH = a\sin B.\sin C\) (đpcm). b) \(BH = a{\cos ^2}B\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(AB = BC.\cos B = a\cos B\) Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có: \( \Rightarrow A{B^2} = BH.BC\)\( \Leftrightarrow {\left( {a\cos B} \right)^2} = BH.a\)\( \Leftrightarrow BH = a{\cos ^2}B\) (đpcm)
|