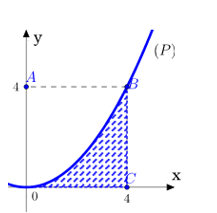
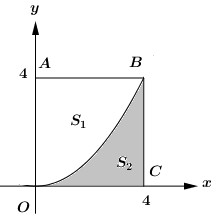
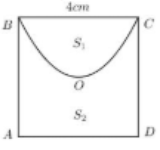
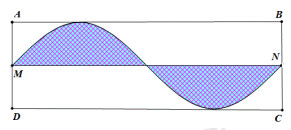
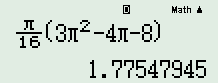50 bài tập ứng dụng tích phân trong hình học mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường parabol (P) có đỉnh tại O. Gọi S là hình phẳng không bị gạch (như hình vẽ). Tính thể tích V của khối tròn xoay khi cho phần S quay quanh trục Ox
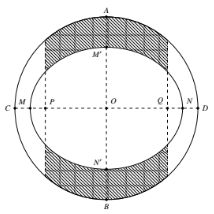
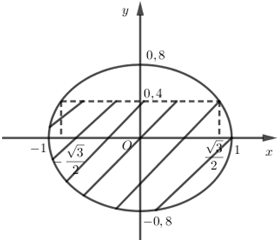
Đáp án: D Phương pháp giải: - Viết phương trình parabol. - Sử dụng công thức tính thể tích khối tròn xoay khi quay hình phẳng (H) giới hạn bởi các đồ thị y=f(x),y=g(x), các đường thẳng x=a,x=b là V=πb∫a|f2(x)−g2(x)|dx. Lời giải chi tiết: Phương trình parabol (P) có dạng y=ax2 đi qua điểm B(4;4) ⇒4=a.42⇔a=14 nên (P):y=14x2. Gọi (H) là phần diện tích hình phẳng giới hạn bởi đường thẳng y=4, đồ thị hàm số y=14x2, đường thẳng x=0. Khi đó thể tích khối tròn xoay tạo thành khi quay (H) quanh Ox là : V=π4∫0[42−(14x2)2]dx=π4∫0(16−116x4)dx =π(16x−x516.5)|40=π(16.4−4516.5)=256π5 Chọn D Câu hỏi 2 : Một khu vườn dạng hình tròn có hai đường kính AB,CD vuông góc với nhau, AB=12m. Người ta làm một hồ cá có dạng hình elip với bốn đỉnh M,N,M′,N′ như hình vẽ, biết MN=10m,M′N′=8m, PQ=8m. Diện tích phần trồng cỏ (phần gạch sọc) bằng:
Đáp án: D Phương pháp giải: +) Đặt trục tọa độ, lập phương trình đường tròn, phương trình elip. +) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x),y=g(x), đường thẳng x=a,x=b(a<b) là S=b∫a|f(x)−g(x)|dx. Lời giải chi tiết:
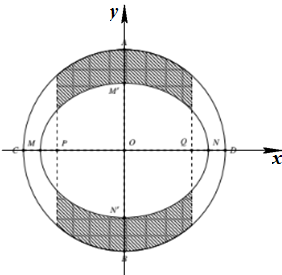
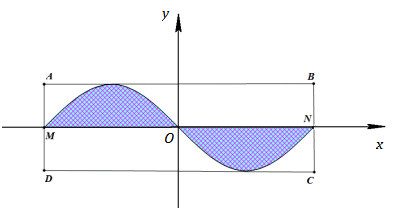
Đặt hệ trục tọa độ như hình vẽ. Ta có AB=12m⇒OA=6m. Phương trình đường tròn là x2+y2=36⇔y=±√36−x2. Phương trình elip là: x225+y216=1⇔y=±4√1−x225. Khi đó diện tích phần trồn cỏ là: S=24∫−4(√36−x2−4√1−x225)dx≈32,03(m2). Chọn D Câu hỏi 3 : Tính thể tích vật thể có đáy là một hình tròn giới hạn bởi đường tròn có phương trình x2+y2=1 và mỗi thiết diện vuông góc với trục Ox là một hình vuông (tham khảo hình vẽ bên).
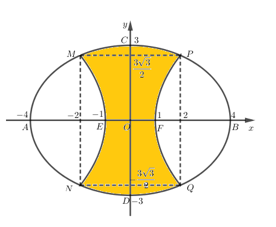
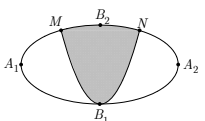
Đáp án: A Phương pháp giải: Sử dụng công thức tính thể tích phần vật thể giới hạn bởi hai mặt phẳng x=a,x=b là V=b∫aS(x)dx, ở đó S(x) là diện tích thiết diện khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x(a≤x≤b). Lời giải chi tiết: Quan sát hình vẽ, ta thấy thiết diện là hình vuông cạnh AB. Gọi H=AB∩Ox⇒OH=x,OA=1⇒AH=√1−x2 ⇒AB=2√1−x2⇒S(x)=AB2=4(1−x2). Vật thể đã cho giới hạn bởi hai mặt phẳng x=−1,x=1 và có diện tích thiết diện S(x)=4(1−x2) nên có thể tích V=1∫−14(1−x2)dx=(4x−43x3)|1−1=163. Chọn A. Câu hỏi 4 : Vườn hoa của một trường học có hình dạng được giới hạn bởi một đường elip có bốn đỉnh A,B,C,D và hai đường parabol có các đỉnh lần lượt là E,F (phần tô đậm của hình vẽ bên). Hai đường parabol có cùng trục đối xứng AB, đối xứng với nhau qua trục CD, hai parabol cắt elip tại các điểm M,N,P,Q. Biết AB=8m,CD=6m,MN=PQ=3√3m,EF=2m. Chi phí để trồng hoa trên vườn là 300.000 đ/m2 . Hỏi số tiền trồng hoa cho cả vườn gần nhất với số tiền nào dưới đây?
Đáp án: D Phương pháp giải: - Viết phương trình elip và parabol. - Tính diện tích hình phẳng (phần màu trắng) giới hạn bởi nửa elip bên phải trục CD và parabol bên phải trục CD. Lời giải chi tiết: Gắn hệ trục tọa độ như hình vẽ, dễ thấy B(4;0),C(0;3),F(1;0). Ta chỉ cần xét phần bên phải trục Oy vì hình vẽ có tính đối xứng. Phương trình elip: (E):x216+y29=1⇒x=4√1−y29. Dễ thấy PQ=3√3⇒P(m;3√32) với m>0. Mà P∈(E)⇒m=4√1−27/49=2⇒P(2;3√32). Gọi phương trình parabol bên phải trục tung là (P):x=ay2+by+c. Đỉnh F(1;0)⇒c=1,b=0⇒x=ay2+1 P∈(P):x=ay2+1⇔2=a.(3√32)2+1⇔274a+1=2⇔a=427 ⇒(P):x=427y2+1. Diện tích hình phẳng giới hạn bởi elip (E) và parabol (P) (phần màu trắng) nên phải trục tung là: S1=3√32∫−3√32[4√1−y29−427y2−1]dy⇒2S1≈21,6686 Diện tích elip: S=πab=π.4.3=12π. Diện tích phần tô màu đậm là S−2S1≈16,03. Số tiền trồng hoa là: 16,03.300.000=4.809.000 Chọn D.
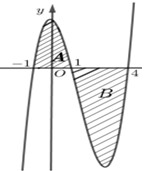
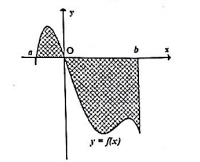
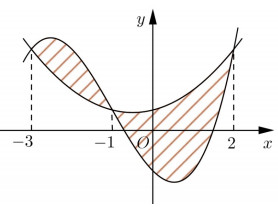
Câu hỏi 5 : Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Diện tích hai phần A và B lần lượt là 163 và 634. Tính 32∫−1f(2x+1)dx.
Đáp án: C Phương pháp giải: Sử dụng phương pháp đổi biến số để đưa tích phân về biến t. Sử dụng công thức c∫af(x)dx=b∫af(x)dx+c∫bf(x)dx. Lời giải chi tiết: Xét 32∫−1f(2x+1)dx. Đặt 2x+1=t⇔2dx=dt⇔dx=dt2. Đổi cận:{x=−1⇒t=−1x=32⇒t=4. Khi đó ta có 32∫−1f(2x+1)dx=124∫−1f(t)dt=124∫−1f(x)dx=12(1∫−1f(x)dx+4∫1f(x)dx) Từ hình vẽ ta có 1∫−1f(x)dx=163;4∫1f(x)dx=−634 Nên 32∫−1f(2x+1)dx=12(1∫−1f(x)dx+4∫1f(x)dx)=12(163−634)=−12524 Chọn C. Câu hỏi 6 : Hình phẳng giới hạn bởi các đường cong y=x(1−x) và y=x3−x có diện tích bằng:
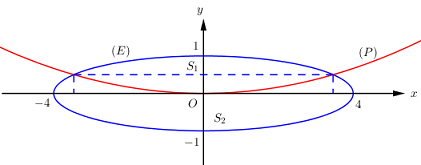
Đáp án: A Phương pháp giải: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x),y=g(x),x=a,x=b(a<b) là S=b∫a|f(x)−g(x)|dx. Lời giải chi tiết: Xét phương trình hoành độ giao điểm x(1−x)=x3−x⇔x−x2=x3−x⇔x3+x2−2x=0⇔[x=0x=1x=−2. Vậy S=|0∫−2(x3+x2−2x)dx|+|1∫0(x3+x2−2x)dx|=83+512=3712. Chọn A Câu hỏi 7 : Biết rằng parabol y=124x2 chia hình giới hạn bởi elip có phương trình x216+y21=1 thành hai phần có diện tích lần lượt là S1,S2 với S1<S2. Tỉ số S1S2 bằng:
Đáp án: A Phương pháp giải: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x),y=g(x),x=a,x=b(a<b) là S=b∫a|f(x)−g(x)|dx. Lời giải chi tiết:
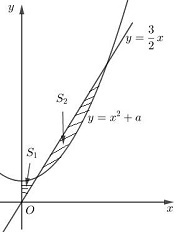
Parabol y=124x2 chia hình giới hạn bởi elip có phương trình x216+y21=1⇔y=±√1−x216 thành hai phần có diện tích lần lượt là S1,S2(S1<S2)được kí hiệu như hình vẽ. Xét phương trình hoành độ giao điểm 124x2=√1−x216⇔x4576=1−x216⇔x2=12⇔x=±2√3. Khi đó ta có: S1=2√3∫−2√3(√1−x216−124x2)dx≈4,766. Diện tích elip là S(E)=πab=π.4.1=4π⇒S2=S(E)−S1=7,8. Vậy S1S2≈0,6123. Chọn A Câu hỏi 8 : Cho đường thẳng y=32x và parabol y=x2+a (a là tham số thực dương). Gọi S1 và S2 lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi S1=S2 thì a thuộc khoảng nào dưới đây ?
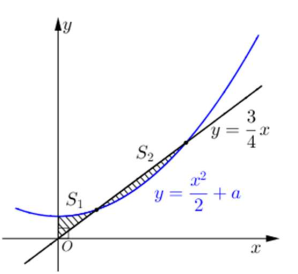
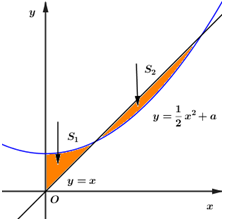
Đáp án: B Phương pháp giải: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x);y=g(x), đường thẳng x=a,x=b là S=b∫a|f(x)−g(x)|dx Lời giải chi tiết: Xét phương trình hoành độ giao điểm x2+a=32x⇔2x2−3x+2a=0(∗). Phương trình có 2 nghiệm phân biệt ⇔Δ=9−8a>0⇔a<98. Kết hợp điều kiện đề bài ⇒0<a<98. Gọi x1,x2(x1<x2) là 2 nghiệm của phương trình (*). Khi đó ta có: S1=x1∫0(x2+a−32x)dx=(x33+ax−3x24)|x10=x313+ax1−3x214S2=x2∫x1(32x−x2−a)dx=(3x24−x33−ax)|x2x1=(3x224−x323−ax2)−(3x214−x313−ax1) Theo bài ra ta có: S1=S2 ⇔x313+ax1−3x214=(3x224−x323−ax2)−(3x214−x313−ax1)⇔3x224−x323−ax2=0⇔9x22−4x32−12ax2=0⇔x2(4x22−9x2+12a)=0⇔[x2=04x22−9x2+12a=0 TH1: x2=0⇒ Thay vào (*) ta có 2a=0⇔a=0(ktm). TH2: 4x22−9x2+12a=0 (1). Vì x2 là nghiệm của (*) nên 2x22−3x2+2a=0⇔12x22−18x2+12a=0 (2). Trừ vế theo vế của (2) cho (1) ta được 8x22−9x2=0⇔[x2=0x2=98. Với x2=0⇔2a=0⇔a=0(ktm). Với x2=98⇔2.(98)2−3.98+2a=0⇔a=2764(tm)=0,421875. Vậy a∈(25;920). Chọn B Câu hỏi 9 : Cho đường thẳng y=34x và parabol y=12x2+a (a là tham số thực dương). Gọi S1 và S2 lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình bên. Khi S1=S2 thì a thuộc khoảng nào dưới đây?
Đáp án: B Phương pháp giải: - Xét phương trình hoành độ giao điểm, tìm điều kiện để phương trình có hai nghiệm phân biệt. - Viết công thức tính hai phần diện tích S1,S2. - Sử dụng điều kiện S1=S2 tìm a. Lời giải chi tiết: Phương trình hoành độ giao điểm : 34x=12x2+a⇔2x2−3x+4a=0(∗). Ta có (d) cắt (P) tại 2 điểm phân biệt có hoành độ dương nên phương trình (*) có hai nghiệm dương phân biệt ⇔{Δ>0S>0P>0⇔{9−32a>02a>0⇔0<a<932. Gọi hai nghiệm phân biệt của (*) là x1<x2. Ta có : S1=x1∫0(12x2−34x+a)dx=(16x3−38x2+ax)|x10=16x31−38x21+ax1 S2=x2∫x1(−12x2+34x−a)dx=(−16x3+38x2−ax)|x2x1=(−16x32+38x22−ax2)+(16x31−38x21+ax1) Do S1=S2 nên 16x31−38x21+ax1==(−16x32+38x22−ax2)+(16x31−38x21+ax1) 16x32−38x22+ax2=0⇔4x22−9x2+24a=0 Do x2 là nghiệm của phương trình (*) nên ta có hệ phương trình {2x22−3x2+4a=04x22−9x2+24a=0⇔{2x22−3x2+4a=016a−3x2=0⇔{2.2569a2−16a+4a=0x2=16a3⇒5129a2−12a=0⇔[a=0a=27128. Đối chiếu điều kiện của a nên ta có a=27128∈(316;712). Chọn B. Câu hỏi 10 : Diện tích hình phẳng giới hạn bởi trục hoành và đồ thị các hàm số y=x và y=√x+6 bằng
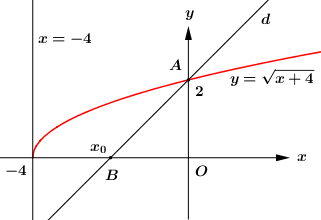
Đáp án: A Phương pháp giải: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=g(x) , đồ thị hàm số y=f(x) và x=a;x=b là S=b∫a|f(x)−g(x)|dx Lời giải chi tiết: Xét phương trình x=√x+6(x≥0) ⇔x2−x−6=0⇔[x=−2(ktm)x=3(tm) Phương trình √x+6=0⇒x=−6 Khi đó, diện tích hình phẳng giới hạn bởi trục hoành và các đồ thị hàm số y=x và y=√x+6 là : S=0∫−6√x+6dx+3∫0(√x+6−x)dx Chọn A. Câu hỏi 11 : Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số y=√x+4, trục hoành và trục tung. Biết đường thẳng d:ax+by−16=0 đi qua A(0;2) và chia (H) thành hai phần có diện tích bằng nhau. Giá trị của a+2b bằng:
Đáp án: A Phương pháp giải: - Tính diện tích của (H). - Gọi B(x0;0)∈d∩Ox, tính diện tích SOAB. - Dựa vào giả thiết suy ra SOAB=12S(H), tìm x0, sau đó tìm a;b. Lời giải chi tiết:
Xét phương trình hoành độ giao điểm của đồ thị hàm số y=√x+4 và trục hoành: √x+4=0⇔x=−4. Suy ra S(H)=0∫−4|√x+4−0|dx=0∫−4√x+4dx=163. Ta có: A(0;2) chính là giao điểm của đường thẳng d và đồ thị hàm số y=√x+4. Gọi B(x0;0)∈d∩Ox, ta có SOAB=12.OA.OB=12.2.|x0|=|x0|. Để đường thẳng d:ax+by−16=0 và chia (H) thành hai phần có diện tích bằng nhau thì x0<0 và SOAB=12S(H). ⇒|x0|=83⇔x0=−83 (Do x0<0). Suy ra đường thẳng d đi qua A(0;2) và B(−83;0), ta có: {2b−16=0−83a−16=0⇔{b=8a=−6. Vậy a+2b=−6+2.8=10. Chọn A. Câu hỏi 12 : Gọi (H) là hình phẳng giới hạn bởi các đường cong y=−x3+12x và y=−x2. Diện tích của (H) bằng:
Đáp án: D Phương pháp giải: Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng x=a,x=b(a<b) và các đồ thị hàm số y=f(x),y=g(x) là: S=b∫a|f(x)−g(x)|dx. Lời giải chi tiết: Xét phương trình hoành độ giao điểm của hai đồ thị hàm số y=−x3+12x và y=−x2 ta được: −x3+12x=−x2⇔x3−x2−12x=0⇔[x=0x=−3x=4⇒SH=0∫−3(−x2+x3−12x)dx+4∫0(−x3+12x+x2)dx=(−x33+x44−6x2)|0−3+(−x44+6x2+x33)|40=994+1603=93712. Chọn D. Câu hỏi 13 : Cho hình phẳng D giới hạn bởi các đường y=ex,y=1,x=2. Tính thể tích khối tròn xoay tạo thành khi cho D quay quanh Ox.
Đáp án: D Phương pháp giải: - Xét phương trình hoành độ giao điểm. - Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y=f(x), y=g(x), đường thẳng x=a, x=b khi quanh quay trục hoành là: V=πb∫a|f2(x)−g2(x)|dx. Lời giải chi tiết: Xét phương trình hoành độ giao điểm: ex=1⇔x=0. Hình phẳng D giới hạn bởi các đường y=ex;y=1, x=0, x=2 có thể tích bằng: V=π2∫0|e2x−1|dx=|π(12e2x−x)|20|=π(12e4−52) Chọn D. Câu hỏi 14 : Cho hình phẳng D giới hạn bởi đường cong y=√lnx, trục hoành và đường thẳng x=3. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích bằng bao nhiêu ?
Đáp án: D Phương pháp giải: - Tìm hoành độ giao điểm của y=√lnx và truc hoành. - Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y=f(x), y=g(x), đường thẳng x=a, x=b khi quanh quay trục hoành là: V=πb∫a|f2(x)−g2(x)|dx. Lời giải chi tiết: Hoành độ giao điểm của y=√lnx và truc hoành là nghiệm của phương trình √lnx=0⇔lnx=0⇔x=1. Thể tích khối tròn xoay là giới hạn bởi y=√lnx, trục hoành và đường thẳng x=3 là: V=π3∫1lnxdx=π(xlnx|31−3∫1x.1xdx)=π(3ln3−3∫1dx)=π(3ln3−2) Chọn D. Câu hỏi 15 : Tính diện tích S của hình phẳng giới hạn bởi đồ thị các hàm số y=x2−2x−2 và y=x+2.
Đáp án: B Phương pháp giải: - Tìm hoành độ giao điểm của các hàm số y=x2−2x−2;y=x+2. - Áp dụng công thức tính diện tích hình phẳng giới hạn bởi các đồ thị hàm số y=f(x), y=g(x), đường thẳng x=a,x=b là: S=b∫a|f(x)−g(x)|dx. Lời giải chi tiết: Hoành độ giao điểm của các hàm số y=x2−2x−2;y=x+2 là nghiệm của phương trình x2−2x−2=x+2⇔x2−3x−4=0⇔[x=4x=−1 Vậy diện tích S=4∫−1|x2−3x−4|dx=1256. Chọn B. Câu hỏi 16 : Tính diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y=x3−3x+2 và y=x+2.
Đáp án: A Phương pháp giải: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), y=g(x), đường thẳng x=a, x=b là: S=b∫a|f(x)−g(x)|dx. Lời giải chi tiết: Xét phương trình hoành độ giao điểm: x3−3x+2=x+2⇔x3−4x=0⇔[x=0x=2x=−2. Khi đó diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y=x3−3x+2 và y=x+2 là: V=2∫−2|x3−4x|dx=0∫−2|x3−4x|dx+2∫0|x3−4x|dx=|0∫−2(x3−4x)dx|+|2∫0(x3−4x)dx|=4+4=8 Chọn A. Câu hỏi 17 : Thể tích khối tròn xoay sinh ra khi cho mặt phẳng giới hạn bởi các đường thẳng y=sinx;y=0;x=0;x=2π quay quanh trục Ox là:
Đáp án: D Phương pháp giải: - Xét phương trình hoành độ giao điểm, tìm các nghiệm thuộc [0;2π]. - Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y=f(x), y=g(x), đường thẳng x=a, x=b khi quanh quay trục hoành là: V=πb∫a|f2(x)−g2(x)|dx. Lời giải chi tiết: Xét phương trình hoành độ giao điểm: sinx=0⇔x=kπ. Trên [0;2π] phương trình trên có 3 nghiệm x=0,x=π,x=2π. Hình phẳng giới hạn bởi các đường y=sinx; y=0; x=0; x=2π quay quanh trục Ox là : V=π2π∫0|sin2x|dx=π(π∫0|sin2x|dx+2π∫π|sin2x|dx)=π(|π∫0sin2xdx|+|2π∫πsin2xdx|) Xét nguyên hàm: ∫sin2dx ta có: ∫sin2dx=12∫(1−cos2x)dx=12(x−12sin2x)+C =12x−14sin2x+C. Khi đó ta có: V=π(|12x−14sin2x|π0|+|12x−14sin2x|2ππ|)=π(12π+12.2π−12π)=π2 Chọn D. Câu hỏi 18 : Cho hình phẳng (H) giới hạn bởi đồ thị y=2x−x2 và trục hoành. Thể tích V của vật thể tròn xoay sinh ra khi quay (H) quanh trục Ox là:
Đáp án: B Phương pháp giải: - Xét phương trình hoành độ giao điểm, tìm các nghiệm thuộc [1;2]. - Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y=f(x), y=g(x), đường thẳng x=a, x=b khi quanh quay trục hoành là: V=πb∫a|f2(x)−g2(x)|dx. Lời giải chi tiết: Xét phương trình hoành độ giao điểm: 2x - {x^2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 0\end{array} \right. Hình phẳng giới hạn bởi đồ thị y = 2x - {x^2} và trục hoành có thể tích là V = \pi \int\limits_0^2 {{{\left( {2x - {x^2}} \right)}^2}dx} = \dfrac{{16}}{{15}}\pi ( sử dụng máy tính) Chọn B. Câu hỏi 19 : Diện tích của hình phẳng giới hạn bởi đồ thị hàm số y = {x^3} - 6{x^2} + 8x với trục hoành là
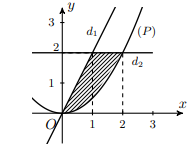
Đáp án: B Phương pháp giải: - Xét phương trình hoành độ giao điểm. - Diện tích khối tròn xoay giới hạn bởi đồ thị hàm số y = f\left( x \right), y = g\left( x \right), đường thẳng x = a, x = b khi quanh quay trục hoành là: V = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} . Lời giải chi tiết: Xét phương trình hoành độ giao điểm: {x^3} - 6{x^2} + 8x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 2\\x = 0\end{array} \right. Khi đó ta có: \begin{array}{l}S = \int\limits_0^4 {\left| {{x^3} - 6{x^2} + 8x} \right|dx} \\S = \int\limits_0^2 {\left| {{x^3} - 6{x^2} + 8x} \right|dx} + \int\limits_2^4 {\left| {{x^3} - 6{x^2} + 8x} \right|dx} \\S = \left| {\int\limits_0^2 {\left( {{x^3} - 6{x^2} + 8x} \right)dx} } \right| + \left| {\int\limits_2^4 {\left( {{x^3} - 6{x^2} + 8x} \right)dx} } \right|\\S = 4 + 4 = 8\end{array} Chọn B. Câu hỏi 20 : Tính diện tích hình phẳng \left( H \right) (phần gạch sọc như hình vẽ) giới hạn bởi ba đường \left( P \right):y = \dfrac{1}{2}{x^2},{d_1}:y = 2x và {d_2}:y = 2.
Đáp án: D Phương pháp giải: - Chia diện tích cần tính thành những phần nhỏ. - Diện tích khối tròn xoay giới hạn bởi đồ thị hàm số y = f\left( x \right), y = g\left( x \right), đường thẳng x = a, x = b khi quanh quay trục hoành là: V = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} . Lời giải chi tiết: Gọi {S_1} là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2x,\,\,y = \dfrac{1}{2}{x^2}, đường thẳng x = 0,\,\,x = 1. \Rightarrow {S_1} = \int\limits_0^1 {\left( {2x - \dfrac{1}{2}{x^2}} \right)dx} = \dfrac{5}{6}. Gọi {S_2} là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 2,\,\,y = \dfrac{1}{2}{x^2}, đường thẳng x = 1,\,\,x = 2. \Rightarrow {S_2} = \int\limits_1^2 {\left( {2 - \dfrac{1}{2}{x^2}} \right)dx} = \dfrac{5}{6}. Vậy S = {S_1} + {S_2} = \dfrac{5}{6} + \dfrac{5}{6} = \dfrac{5}{3}. Chọn D. Câu hỏi 21 : Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = \dfrac{{x + 1}}{{x - 2}} và các trục tọa độ là
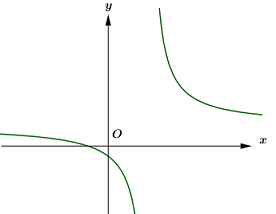
Đáp án: B Phương pháp giải: - Tìm giao của đồ thị hàm số với các trục tọa độ. - Diện tích khối tròn xoay giới hạn bởi đồ thị hàm số y = f\left( x \right), y = g\left( x \right), đường thẳng x = a, x = b khi quanh quay trục hoành là: V = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} . Lời giải chi tiết: Đồ thị hàm số:
Giao của đồ thị hàm số với trục Oy là điểm \left( { - 1;0} \right). Bài toán trở thành: Tính diện tích hình phẳng giới hạn bởi y = \dfrac{{x + 1}}{{x - 2}}, y = 0,\,\,x = - 1,\,\,x = 0. Khi đó diện tích cần tính là: \begin{array}{l}S = \int\limits_{ - 1}^0 {\left| {\dfrac{{x + 1}}{{x - 2}}} \right|dx} = - \int\limits_{ - 1}^0 {\dfrac{{x + 1}}{{x - 2}}dx} \\S = - \int\limits_{ - 1}^0 {\left( {1 + \dfrac{3}{{x - 2}}} \right)dx} \\S = - \left. {\left( {x + 3\ln \left| {x - 2} \right|} \right)} \right|_{ - 1}^0\\S = - \left( {3\ln 2 - \left( { - 1 + 3\ln 3} \right)} \right)\\S = - 3\ln 2 - 1 + 3\ln 3\\S = 3\ln \dfrac{3}{2} - 1\end{array} Chọn B. Câu hỏi 22 : Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường:
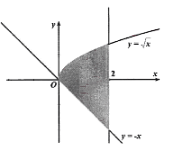
Đáp án: A Phương pháp giải: - Xét phương trình hoành độ giao điểm, tìm các nghiệm thuộc \left[ {0;3} \right]. - Thể tích khối tròn xoay giới hạn bởi đồ thị hàm số y = f\left( x \right), y = g\left( x \right), đường thẳng x = a, x = b khi quanh quay trục hoành là: V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} . Lời giải chi tiết: Xét phương trình hoành độ giao điểm: {x^2} - 4x + 4 = 0 \Leftrightarrow x = 2. Thể tích khối tròn xoay khi quay hình giới hạn bởi y = {x^2} - 4x + 4,y = 0,x = 0,x = 3 xung quanh trục Ox là: \begin{array}{l}V = \pi \int\limits_0^3 {\left| {{{\left( {{x^2} - 4x + 4} \right)}^2}} \right|dx} \\\,\,\,\,\, = \pi \left( {\left| {\int\limits_0^2 {{{\left( {{x^2} - 4x + 4} \right)}^2}dx} } \right| + \left| {\int\limits_2^3 {{{\left( {{x^2} - 4x + 4} \right)}^2}dx} } \right|} \right)\\\,\,\,\,\pi \left( {\dfrac{{32}}{5} + \dfrac{1}{5}} \right) = \dfrac{{33\pi }}{5}\end{array} Chọn A. Câu hỏi 23 : Diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = \sqrt x ;y = x - 2;y = - x là
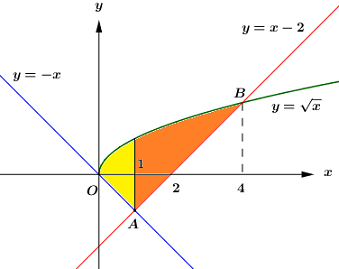
Đáp án: D Phương pháp giải: - Vẽ đồ thị hàm số, xác định các giao điểm. - Chia diện tích cần tính thành các diện tích các hình phẳng giới hạn bởi các đồ thị hàm số y = f\left( x \right), y = g\left( x \right), x = a,\,\,x = b. - Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right), y = g\left( x \right), đường thẳng x = a,\,\,x = b là: S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} . Lời giải chi tiết:
Xét các phương trình hoành độ giao điểm: \begin{array}{l} - x = x - 2 \Leftrightarrow x = 1\\x - 2 = \sqrt x \Leftrightarrow x = 4\end{array} Ta xác định được {x_A} = 1,\,\,{x_B} = 4. Diện tích hình phẳng cần tính bao gồm: - {S_1}: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = \sqrt x ,\,\,y = - x, x = 0,\,\,x = 1. \begin{array}{l} \Rightarrow {S_1} = \int\limits_0^1 {\left( {\sqrt x - \left( { - x} \right)} \right)dx} = \left. {\left( {\dfrac{2}{3}\sqrt {{x^3}} + \dfrac{{{x^2}}}{2}} \right)} \right|_0^1\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{2}{3} + \dfrac{1}{2} - 0 = \dfrac{7}{6}\end{array} - {S_2}: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = \sqrt x ,\,\,y = x - 2, x = 1,\,\,x = 4. \begin{array}{l} \Rightarrow {S_1} = \int\limits_1^4 {\left( {\sqrt x - \left( {x - 2} \right)} \right)dx} = \left. {\left( {\dfrac{2}{3}\sqrt {{x^3}} - \dfrac{{{x^2}}}{2} + 2x} \right)} \right|_1^4\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{2}{3}.8 - 8 + 8 - \dfrac{2}{3} + \dfrac{1}{2} - 2 = \dfrac{{19}}{6}\end{array} Vậy diện tích cần tính là: S = {S_1} + {S_2} = \dfrac{7}{6} + \dfrac{{19}}{6} = \dfrac{{13}}{3}. Chọn D. Câu hỏi 24 : Hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường cong \left( C \right) có phương trình y = \dfrac{1}{4}{x^2}. Gọi {S_1};\,\,{S_2} lần lượt là diện tích phần không bị gạch và phần bị gạch như hình bên dưới. Tỉ số \dfrac{{{S_1}}}{{{S_2}}} bằng.
Đáp án: D Phương pháp giải: - {S_2} là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = \dfrac{1}{4}{x^2}, trục hoành, đường thẳng x = 0 và x = 4. - Cho hai hàm số f\left( x \right);g\left( x \right) liên tục trên đoạn \left[ {a;b} \right]. Diện tích hình phẳng giới hạn bởi đồ thị y = f\left( x \right),y = g\left( x \right) và các đường thẳng x = a,x = b bằng S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} . - Tính {S_1} = {S_{OABC}} - {S_2}. - Tính tỉ số \dfrac{{{S_1}}}{{{S_2}}}. Lời giải chi tiết: Ta thấy {S_2} là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = \dfrac{1}{4}{x^2}, trục hoành, đường thẳng x = 0 và x = 4 nên {S_2} = \int\limits_0^4 {\dfrac{1}{4}{x^2}dx} = \dfrac{{16}}{3}. Ta có: OABC là hình vuông cạnh 4 nên {S_{ABCO}} = {4^2} = 16. \Rightarrow {S_1} = {S_{OABC}} - {S_2} = 16 - \dfrac{{16}}{3} = \dfrac{{32}}{3}. Vậy \dfrac{{{S_1}}}{{{S_2}}} = \dfrac{{32}}{3}:\dfrac{{16}}{3} = 2. Chọn D. Câu hỏi 25 : Cho hàm số f\left( x \right) liên tục trên đoạn \left[ {a;b} \right] và thỏa mãn \int\limits_a^0 {f\left( x \right)dx = m} , \int\limits_0^b {f\left( x \right)dx = n} . Diện tích hình phẳng trong hình vẽ bằng
Đáp án: B Phương pháp giải: Cho hàm số f\left( x \right)liên tục \left[ {a;b} \right], diện tích hình phẳng giới hạn bởi đồ thị hàm số f\left( x \right), các đường thẳng x = a,\,\,x = b và trục Ox là S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} . Lời giải chi tiết: Gọi {S_1} là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right), trục hoành, đường thẳng x = a,\,\,x = 0\,\,\left( {a < 0} \right), ta có {S_1} = \int\limits_a^0 {\left| {f\left( x \right)} \right|dx} = \int\limits_a^0 {f\left( x \right)dx} = m. Gọi {S_2} là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right), trục hoành, đường thẳng x = 0,\,\,x = b\,\,\left( {b > 0} \right), ta có {S_2} = \int\limits_0^b {\left| {f\left( x \right)} \right|dx} = - \int\limits_0^b {f\left( x \right)dx} = - n. Vậy diện tích cần tính là S = {S_1} + {S_2} = m - n. Chọn B. Câu hỏi 26 : Tính diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = {x^3} - x và đồ thị hàm số y = x - {x^2}.
Đáp án: D Phương pháp giải: - Giải phương trình hoành độ giao điểm. - Cho hàm số f\left( x \right)liên tục \left[ {a;b} \right], diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right),y = g\left( x \right), các đường thẳng x = a,\,\,x = b là S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} . Lời giải chi tiết: Xét phương trình hoành độ giao điểm: {x^3} - x = x - {x^2} \Leftrightarrow {x^3} + {x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = - 2\end{array} \right. Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số y = {x^3} - x và y = x - {x^2} là \begin{array}{l}S = \int\limits_{ - 2}^1 {\left| {{x^3} + {x^2} - 2x} \right|dx} \\\,\,\,\,\, = \left| {\int\limits_{ - 2}^0 {\left( {{x^3} + {x^2} - 2x} \right)dx} } \right| + \left| {\int\limits_0^1 {\left( {{x^3} + {x^2} - 2x} \right)dx} } \right|\\\,\,\,\,\,\, = \dfrac{8}{3} + \dfrac{5}{{12}} = \dfrac{{37}}{{12}}.\end{array} Chọn D. Câu hỏi 27 : Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số y = \sqrt x \cos \dfrac{x}{2},\,\,y = 0,\,\,x = \dfrac{\pi }{2},\,\,x = \pi . Tính thể tích V của khối tròn xoay sinh ra khi cho hình phẳng \left( H \right) quay xung quanh trục Ox.
Đáp án: B Phương pháp giải: Cho hàm số y = f\left( x \right) liên tục trên đoạn \left[ {a;b} \right]. Gọi \left( H \right) là hình thang cong giới hạn bởi đồ thị hàm số y = f\left( x \right), trục Ox và hai đường thẳng x = a và x = b. Thể tích V của khối tròn xoay tạo thanh khi quay \left( H \right) quanh trục Ox được tính theo công thức V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} . Lời giải chi tiết: Xét phương trình hoành độ giao điểm: y = \sqrt x \cos \dfrac{x}{2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\\dfrac{x}{2} = \dfrac{\pi }{2} + k\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pi + k2\pi \end{array} \right. Xét x \in \left[ {\dfrac{\pi }{2};\pi } \right] \Rightarrow x = \pi \Rightarrow V = \pi \int\limits_{\dfrac{\pi }{2}}^\pi {x{{\cos }^2}\dfrac{x}{2}dx} \approx 1,775.
Chọn B. Câu hỏi 28 : Diện tích của hình phẳng giới hạn bởi hai đường thẳng y = 18{x^2} và y = 18x bằng
Đáp án: D Phương pháp giải: - Tìm hoành độ giao điểm hai đồ thị hàm số. - Áp dụng công thức tính diện tích hình phẳng: Cho hàm số f\left( x \right)liên tục \left[ {a;b} \right], diện tích hình phẳng giới hạn bởi đồ thị hàm số f\left( x \right), các đường thẳng x = a,\,\,x = b và trục Ox là S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} . Lời giải chi tiết: Hoành độ giao điểm của đồ thị hàm số y = 18{x^2};y = 18x là nghiệm của phương trình: 18{x^2} = 18x \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right. Diện tích hình phẳng giới hạn bởi đồ thj hàm số y = 18{x^2}; y = 18x là: S = \int\limits_0^1 {\left| {18{x^2} - 18x} \right|d{\rm{x}}} = - \int\limits_0^1 {\left( {18{x^2} - 18x} \right)dx} = 3 Chọn D. Câu hỏi 29 : Cho hình phẳng D giới hạn bởi các đường y = \sqrt x ,y = - x,x = 2 (phần tô đậm trong hình). Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích bằng bao nhiêu?
Đáp án: B Phương pháp giải: - Tìm hoành độ giao điểm của các hàm số y = {x^2} - 2x - 2;y = x + 2. - Áp dụng công thức tính thể tích hình phẳng giới hạn bởi các đồ thị hàm số y = f\left( x \right), y = g\left( x \right), đường thẳng x = a,\,\,x = b là: V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx} . Lời giải chi tiết: Xét phương trình hoành độ giao điểm \sqrt x = - x \Leftrightarrow \left\{ \begin{array}{l} - x \ge 0\\x = {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \le 0\\\left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\end{array} \right. \Leftrightarrow x = 0. Thể tích khối tròn xoay cần tính là: V = \pi \int\limits_0^2 {\left| {x - {x^2}} \right|dx} = \dfrac{{2\pi }}{3}. Chọn B. Câu hỏi 30 : Cho hình phẳng \left( H \right) giới hạn bởi parabol y = a{x^2} + 1\,\,\,\left( {a > 0} \right), trục tung và đường thẳngx = 1. Quay \left( H \right)quanh trục Ox được một khối tròn xoay có thể tích bằng \dfrac{{28}}{{15}}\pi . Mệnh đề nào dưới đây đúng?
Đáp án: B Phương pháp giải: Sử dụng ứng dụng của tích phân trong tính thể tích khối tròn xoay Lời giải chi tiết: \begin{array}{l}V = \dfrac{1}{2}.\left( {\int\limits_0^1 {\dfrac{{\sqrt 3 .4{{\left( {1 - x} \right)}^2}}}{4} + \int\limits_{ - 1}^0 {\dfrac{{\sqrt 3 .4{{\left( {x + 1} \right)}^2}}}{4}} } } \right)\\ = \dfrac{{\sqrt 3 }}{2}.\left( {\dfrac{1}{3} + \dfrac{1}{3}} \right) = \dfrac{\sqrt 3 }{3} \end{array} Vậy 0 < a < 2 Chọn B. Câu hỏi 31 : Cho vật thể có mặt đáy là hình tròn có bán kính bằng 1, tâm trùng gốc tọa độ (hình vẽ). Khi cắt vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \left( { - 1 \le x \le 1} \right)thì được thiết diện là một tam giác đều. Tính thể tích V của vật thể đó.
Đáp án: B Phương pháp giải: Sử dụng ứng dụng của tích phân trong tính thể tích của khối tròn xoay Lời giải chi tiết: Độ dài cạnh của tam giác đều cắt trục Ox là a = 2.\sqrt {1 - {x^2}} Diện tích tam giác đều đó là S = \dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{4\left( {1 - {x^2}} \right)\sqrt 3 }}{4} = \sqrt 3 \left( {1 - {x^2}} \right) Thể tích vật thể là V = \int\limits_{ - 1}^1 {Sdx} = \int\limits_{ - 1}^1 {\sqrt 3 \left( {1 - {x^2}} \right)dx} = \dfrac{{4\sqrt 3 }}{3} Chọn B Câu hỏi 32 : Cho hình vuông ABCD tâm O, độ dài cạnh là 4cm. Đường cong BOC là một phần của parabol đỉnh O chia hình vuông thành hai hình phẳng có diện tích lần lượt là {S_1} và {S_2} (tham khảo hình vẽ).
Tỉ số \dfrac{{{S_1}}}{{{S_2}}} bằng:
Đáp án: A Phương pháp giải: Cách 1: Sử dụng ứng tích phân để tính diện tích hình phẳng. Cách 2: Sử dụng công thức tính nhanh diện tích của parabol: {S_1} = \frac{4}{3}Rh. {S_2} = {S_{ABCD}} - {S_1} \Rightarrow \frac{{{S_1}}}{{{S_2}}} = ... Lời giải chi tiết:
Gọi H là trung điểm của BC. \begin{array}{l}{S_1} = \frac{4}{3}Rh = \frac{4}{3}.HC.OH = \frac{4}{3}.2.2 = \frac{{16}}{3}\,{m^2}.\\{S_{ABCD}} = {4^2} = 16\\ \Rightarrow {S_2} = {S_{ABCD}} - {S_1} = 16 - \frac{{16}}{3} = \frac{{32}}{3}\,\,{m^2}.\\ \Rightarrow \frac{{{S_1}}}{{{S_2}}} = \frac{{16}}{3}:\frac{{32}}{3} = \frac{1}{2}.\end{array} Chọn A. Câu hỏi 33 : Cho F\left( x \right) là một nguyên hàm của f\left( x \right) trên đoạn \left[ { - 1;3} \right]. Biết F\left( { - 1} \right) = 2,F\left( 3 \right) = \dfrac{{11}}{2}, tính tích phân I = \int\limits_{ - 1}^3 {\left[ {2f\left( x \right) - x} \right]dx.}
Đáp án: B Phương pháp giải: - Sử dụng tính chất tích phân: \int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} . - Với F\left( x \right) là một nguyên hàm của f\left( x \right) thì \int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right). Lời giải chi tiết: Ta có: \begin{array}{l}I = \int\limits_{ - 1}^3 {\left[ {2f\left( x \right) - x} \right]dx} = 2\int\limits_{ - 1}^3 {f\left( x \right)dx} - \int\limits_{ - 1}^3 {xdx} \\\,\,\,\, = 2\left( {F\left( 3 \right) - F\left( { - 1} \right)} \right) - \left. {\dfrac{{{x^2}}}{2}} \right|_{ - 1}^3\\\,\,\,\, = 2\left( {\dfrac{{11}}{2} - 2} \right) - \left( {\dfrac{9}{2} - \dfrac{1}{2}} \right) = 3.\end{array} Chọn B. Câu hỏi 34 : Diện tích hình phẳng giới hạn bởi đường y = 4 - \left| x \right| và trục hoành là
Đáp án: B Phương pháp giải: - Giải phương trình hoành độ giao điểm của đường thẳng y = 4 - \left| x \right| với trục hoành để xác định các cận. - Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right), trục hoành, đường thẳng x = a,\,\,x = b là: S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} . Lời giải chi tiết: Xét phương trình hoành độ giao điểm 4 - \left| x \right| = 0 \Leftrightarrow \left| x \right| = 4 \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = - 4\end{array} \right.. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = 4 - \left| x \right| và trục hoành là: \begin{array}{l}S = \int\limits_{ - 4}^4 {\left| {4 - \left| x \right|} \right|dx} = \int\limits_{ - 4}^0 {\left( {x + 4} \right)dx} + \int\limits_0^4 {\left( {4 - x} \right)dx} \\\,\,\,\, = \left. {\left( {\dfrac{{{x^2}}}{2} + 4x} \right)} \right|_{ - 4}^0 + \left. {\left( {4x - \dfrac{{{x^2}}}{2}} \right)} \right|_0^4\\\,\,\,\, = 8 + 8 = 16.\end{array} Chọn B. Câu hỏi 35 : Cho hàm số y = f\left( x \right) liên tục và nhận giá trị dương trên \mathbb{R}. Gọi {D_1} là hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right), các đường x = 0,\,\,x = 1 và trục Ox. Gọi {D_2} là hình phẳng giới hạn bởi đồ thị hàm số y = \dfrac{1}{3}f\left( x \right), các đường x = 0,\,\,\,x = 1 và trục Ox. Quay các hình phẳng {D_1},\,\,{D_2} quanh trục Ox ta được các khối tròn xoay có thể tích lần lượt là {V_1},\,\,{V_2}. Khẳng định nào sau đâu là đúng?
Đáp án: A Phương pháp giải: Công thức tính thể tích của khối tròn xoay được tạo bởi các đường thẳng x = a,\;x = b\;\;\left( {a < b} \right) và các đồ thị hàm số y = f\left( x \right),\;y = g\left( x \right) khi quay quanh trục Ox là: V = \pi \int\limits_a^b {\left| {{f^2}\left( x \right) - {g^2}\left( x \right)} \right|dx.} Lời giải chi tiết: Ta có: {V_1} = \pi \int\limits_0^1 {{f^2}\left( x \right)dx} và {V_2} = \pi \int\limits_0^1 {{{\left[ {\dfrac{1}{3}f\left( x \right)} \right]}^2}dx} = \dfrac{1}{9}\pi \int\limits_0^1 {{f^2}\left( x \right)dx} \Rightarrow {V_1} = 9{V_2}. Chọn A. Câu hỏi 36 : Hình phẳng \left( H \right) có diện tích bằng S, gấp 2 lần diện tích hình phẳng được giới hạn bởi đồ thị các hàm số y = {x^2} - 4,\,\,y = 2x - 4. Tính diện tích S?
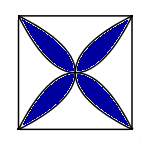
Đáp án: C Phương pháp giải: Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng x = a,\;x = b\;\;\left( {a < b} \right) và các đồ thị hàm số y = f\left( x \right),\;y = g\left( x \right) là: S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx.} Lời giải chi tiết: Xét phương trình hoành độ giao điểm của hai đồ thị hàm số y = {x^2} - 4 và y = 2x - 4 là: {x^2} - 4 = 2x - 4 \Leftrightarrow {x^2} - 2x = 0 \Leftrightarrow x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right. Gọi {S_0} là diện tích hình phẳng được giới hạn bởi đồ thị các hàm số y = {x^2} - 4,\,\,y = 2x - 4. \begin{array}{l} \Rightarrow {S_0} = \int\limits_0^2 {\left| {{x^2} - 4 - \left( {2x - 4} \right)} \right|dx} = \int\limits_0^2 {\left( {2x - 4 - {x^2} + 4} \right)dx} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int\limits_0^2 {\left( {2x - {x^2}} \right)dx} = \left. {\left( {{x^2} - \dfrac{{{x^3}}}{3}} \right)} \right|_0^2 = \dfrac{4}{3}\\ \Rightarrow S = 2{S_0} = 2.\dfrac{4}{3} = \dfrac{8}{3}.\end{array} Chọn C. Câu hỏi 37 : Làng gốm truyền thống Bát Tràng dự kiến làm một bức tranh gồm hình vuông cạnh 4\,\,\left( m \right), thiết kế có 4 đường parabol chung đỉnh tại tâm của hình vuông, tạo nên bốn cánh hoa (tham khảo hình vẽ). Phần diện tích cánh hoa (phần tô đậm) sẽ được tráng một lớp men đặc biệt. Chi phí tráng lớp men đó có đơn giá là 24 triệu đồng/{m^2}. Tính số tiền phải trả để tráng men cho 4 cánh hoa.
Đáp án: D Phương pháp giải: - Gắn hệ tọa độ vào hình vẽ đã cho. - Viết phương trình đường parabol tạo thành cánh hoa. - Áp dụngứng dụng tích phân để tính diện tích hình phẳng để tính diện tích phần tráng men. Lời giải chi tiết:
Gắn hệ trục tọa độ như hình vẽ. Parbol đi qua gốc tọa độ và điểm A,\,\,B có phương trình y = \dfrac{{{x^2}}}{2}. Parbol đi qua gốc tọa độ và điểm B,\,\,C có phương trình x = \dfrac{{{y^2}}}{2} \Leftrightarrow {y^2} = 2x \Leftrightarrow y = \sqrt {2x} \,\,\left( {x \ge 0} \right). Diện tích 1 cánh hoa là diện tích hình phẳng giới hạn bởi parabol y = \dfrac{{{x^2}}}{2};y = \sqrt {2x} , đường thẳng x = 2;\,\,x = 0 là {S_1} = \int\limits_0^2 {\left( {\sqrt {2x} - \dfrac{{{x^2}}}{2}} \right)dx} = \dfrac{4}{3}. \Rightarrow Diện tích phần tráng men là: S = 4{S_1} = \dfrac{16}{3}\,\,\left( {{m^2}} \right). Vậy số tiền cần phải trả là T = 24.\dfrac{16}{3} = 128 triệu. Chọn D. Câu hỏi 38 : Cá hồi Thái Bình Dương đến mùa sinh sản chúng thường bơi từ biển đến thượng nguồn con sông để đẻ trứng trên sỏi đá rồi chết. Khi nghiên cứu một con cá hồi sinh sản người ta phát hiện ra một quy luật nó chuyển động trong nước yên lặng là s\left( t \right) = - \frac{{{t^2}}}{{10}} + 4t, với t (giờ) là khoảng thời gian từ lúc con cá bắt đầu chuyển động và s (km) là quãng đường con cá bơi trong khoảng thời gian đó. Nếu thả con cá hồi vào dòng nước có vận tốc dòng nước chảy là 2 km/h. Tính khoảng cách xa mà con cá hồi có thể bơi ngược dòng nước đến nơi đẻ trứng.
Đáp án: B Phương pháp giải: +) v\left( t \right) = s'\left( t \right), tính vận tốc thực của con cá khi bơi ngược dòng. +) s\left( t \right) = \int {v\left( t \right)dt} +) Sử dụng giả thiết S(0) = 0 để tìm hằng số C. +) Tìm GTLN của biểu thức S(t). Lời giải chi tiết: Vận tốc của con cá là v\left( t \right) = s'\left( t \right) = - \frac{t}{5} + 4 Vận tốc thực của con cá khi khi bơi ngược dòng là v\left( t \right) - 2 = \frac{{ - t}}{5} + 4 - 2 = \frac{{ - t}}{5} + 2 Quãng đường con cá bơi được trong thời gian t kể từ lúc bắt đầu là S\left( t \right) = \int\limits_0^t {\left( { - \frac{t}{5} + 2} \right)dt} = - \frac{{{t^2}}}{{10}} + 2t + C Mà S\left( 0 \right) = 0 \Rightarrow C = 0 \Rightarrow S\left( t \right) = - \frac{{{t^2}}}{{10}} + 2t = - \frac{1}{{10}}\left( {{t^2} - 20t} \right) = - \frac{1}{{10}}{\left( {t - 10} \right)^2} + 10 \le 10\,\,\forall t Vậy khoảng cách xa mà con cá hồi có thể bơi ngược dòng nước đến nơi đẻ trứng là 10 km. Chọn B. Câu hỏi 39 : Một công ty phải gánh chịu nợ với tốc độ D(t) đô la mỗi năm, với D'\left( t \right) = 90\left( {t + 6} \right)\sqrt {{t^2} + 12t} , trong đó t là số lượng thời gian (tính theo năm) kể từ khi công ty bắt đầu vay nợ. Đến năm thứ tư công ty phải chịu 1 610 640 đô la tiền nợ nần. Tìm hàm số biểu diễn tốc độ nợ nần của công ty này?
Đáp án: C Phương pháp giải: Thực chất đây là một bài toán tìm nguyên hàm D\left( t \right) = \int {D'\left( t \right)dt} Lời giải chi tiết: Ta có D\left( t \right) = \int {D'\left( t \right)dt} = \int {90\left( {t + 6} \right)\sqrt {{t^2} + 12t} dt} Đặt \sqrt {{t^2} + 12t} = y \Rightarrow {t^2} + 12t = {y^2} \Leftrightarrow \left( {2t + 12} \right)dt = 2ydy \Leftrightarrow \left( {t + 6} \right)dt = ydy \Rightarrow D\left( t \right) = \int {90{y^2}dy} = 30{y^3} + C = 30{\left( {\sqrt {{t^2} + 12t} } \right)^3} + C Vì đến năm thứ tư công ty đã chịu 1610640 tiền nợ nần nên số tiền mà công ty vay năm đầu tiên sẽ được tính 1610640 - 30\sqrt {{{\left( {{4^2} + 12.4} \right)}^3}} = 1595280 Vậy công thức tính tiền nợ nần là D\left( t \right) = 30\sqrt {{{\left( {{t^2} + 12t} \right)}^3}} + 1595280 Chọn C. Câu hỏi 40 : Cho S là diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \left( {{C_1}} \right):\,\,y = {2 \over 3}{x^3} - 3m{x^2} - 2{m^3} và \left( {{C_2}} \right):\,\,y = - {{{x^3}} \over 3} + m{x^2} - 5{m^2}x. Gọi N, n lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của S khi m \in \left[ {1;3} \right]. Tính N - n?
Đáp án: B Phương pháp giải: Giải phương trình hoành độ giao điểm, suy ra các nghiệm x = a,\,\,x = b\,\,\left( {a < b} \right). \Rightarrow S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} Tìm giá trị lớn nhất và nhỏ nhất của hàm số S\left( m \right) trên \left[ {1;3} \right]. Lời giải chi tiết: Xét phương trình hoành độ giao điểm \eqalign{ & {2 \over 3}{x^3} - 3m{x^2} - 2{m^3} = - {{{x^3}} \over 3} + m{x^2} - 5{m^2}x \cr & \Leftrightarrow {x^3} - 4m{x^2} + 5{m^2}x - 2{m^3} = 0 \cr & \Leftrightarrow \left( {x - m} \right)\left( {{x^2} - 3mx + 2{m^2}} \right) = 0 \cr & \Leftrightarrow {\left( {x - m} \right)^2}\left( {x - 2m} \right) = 0 \cr & \Leftrightarrow \left[ \matrix{ x = m \hfill \cr x = 2m \hfill \cr} \right. \cr} m \in \left[ {1;3} \right] \Rightarrow m < 2m và khi x \in \left( {m;2m} \right) \Rightarrow x < 2m \Rightarrow {x^3} - 4m{x^2} + 5{m^2}x - 2{m^3} < 0 Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \left( {{C_1}} \right) và \left( {{C_2}} \right) là: \eqalign{ & S = \int\limits_m^{2m} {\left| {{x^3} - 4m{x^2} + 5{m^2}x - 2{m^3}} \right|dx} = \int\limits_m^{2m} {\left( { - {x^3} + 4m{x^2} - 5{m^2}x + 2{m^3}} \right)dx} \cr & = \left. {\left( { - {{{x^4}} \over 4} + 4m{{{x^3}} \over 3} - 5{m^2}{{{x^2}} \over 2} + 2{m^3}x} \right)} \right|_m^{2m} = {{{m^4}} \over {12}} \cr & m \in \left[ {1;3} \right] \Rightarrow {1 \over {12}} \le S \le {{27} \over 4} \Rightarrow \left\{ \matrix{ N = {{27} \over 4} \hfill \cr n = {1 \over {12}} \hfill \cr} \right. \Rightarrow N - n = {{20} \over 3}. \cr} Chọn B. Câu hỏi 41 : Ông A có một mảnh đất hình chữ nhật ABCD có AB = 2\pi \,\left( m \right),\,\,AD = 5\,\left( m \right). Ông muốn trồng hoa trên giải đất có giới hạn bởi hai đường trung bình MN và đường hình sin (như hình vẽ). Biết kinh phí trồng hoa là 100.000 đồng / m2. Hỏi ông A cần bao nhiêu tiền để trồng hoa trên giải đất đó?
Đáp án: A Phương pháp giải: Gắn hệ trục tọa độ. Xác định hàm số đường hình sin. Xác định các đường giới hạn phần diện tích hình phẳng được tô xanh. Áp dụng công thức ứng dụng tích phân để tính diện tích hình phẳng. Lời giải chi tiết: Gắn hệ trục tọa độ Oxy như hình vẽ:
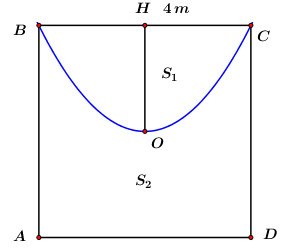
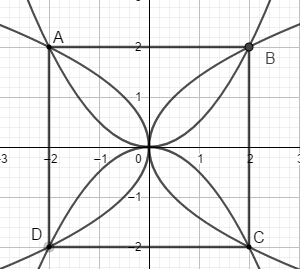
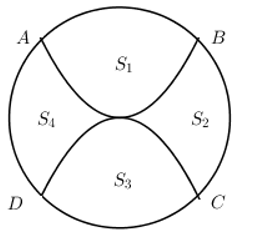
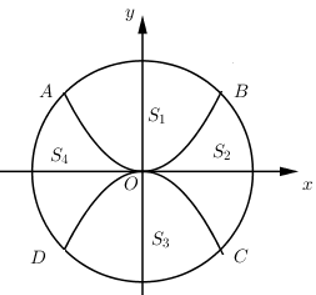
Dựa vào hình vẽ ta thấy đường sin có chu kì bằng AB = 2\pi và biên độ bằng AM = {1 \over 2}AD = {5 \over 2} \Rightarrow Đường hình sin có phương trình y = - {5 \over 2}\sin x. Câu hỏi 42 : Sân trường THPT Chuyên Hà Giang có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích S1, S2 dùng để trồng hoa, phần diện tích S3, S4 dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là 150.000 đồng/ 1 m2, kinh phí trồng cỏ là 100.000 đồng/1m2. Hỏi cả trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn).
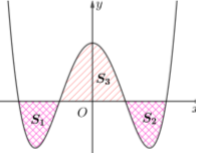
Đáp án: D Phương pháp giải: Gắn hệ trục tọa độ Oxy hợp lý, viết các phương trình đường tròn và phương trình parabol. Ứng dụng tích phân để tính diện tích hình phẳng. Lời giải chi tiết: Gắn hệ trục tọa độ Oxy như hình vẽ, do ABCD là hình vuông cạnh 4m nên ta có A\left( -2;2 \right);B\left( 2;2 \right),C\left( 2;-2 \right);D\left( -2;-2 \right), từ đó ta dễ dàng viết được phương trình đường tròn là {{x}^{2}}+{{y}^{2}}=8 và phương trình 2 parabol là y=\frac{1}{2}{{x}^{2}} và y=-\frac{1}{2}{{x}^{2}}. Ta có: S1 là diện tích hình phẳng giới hạn bởi đường tròn {{x}^{2}}+{{y}^{2}}=8 và parabol (P): y=\frac{1}{2}{{x}^{2}} \begin{align}& \Rightarrow {{S}_{1}}+{{S}_{3}}=4\int\limits_{0}^{2}{\left( \sqrt{8-{{x}^{2}}}-\frac{1}{2}{{x}^{2}} \right)dx}=15,23={{S}_{3}}\,\,\left( {{m}^{2}} \right) \\ & {{S}_{2}}+{{S}_{4}}=2\pi {{\left( 2\sqrt{2} \right)}^{2}}-{{S}_{1}}-{{S}_{3}}=35,04\,\left( {{m}^{2}} \right) \\ \end{align} \Rightarrow Chi phí để trồng bồn hoa đó là: 15,23.150+35,04.100\approx 5790 (nghìn đồng). Chọn D. Câu hỏi 43 : Cho hàm số y={{x}^{4}}-3{{x}^{2}}+m có đồ thị \left( C \right) cắt trục hoành tại 4 điểm phân biệt. Gọi {{S}_{1}} là diện tích hình phẳng giới hạn bởi trục hoành và phần đồ thị \left( C \right) nằm phía trên trục hoành, {{S}_{2}} là diện tích hình phẳng giới hạn bởi trục hoành và phần đồ thị \left( C \right) nằm phía dưới trục hoành. Biết rằng {{S}_{1}}={{S}_{2}}. Giá trị của m là
Đáp án: D Phương pháp giải: +) Tìm tọa độ giao điểm, xác định diện tích hình phẳng để tìm giá trị tham số m. +) Sử dụng công thức ứng dụng tích phân để tính diện tích hình phẳng. Lời giải chi tiết: Phương trình hoành độ giao điểm \left( C \right) và Ox là {{x}^{4}}-3{{x}^{2}}+m=0\,\,\,\,\,\,\,\,\,\,\,\,\left( * \right). Đặt t={{x}^{2}}\ge 0, khi đó \left( * \right)\Leftrightarrow {{t}^{2}}-3t+m=0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( I \right). Để \left( C \right) cắt Ox tại bốn điểm phân biệt khi \left( I \right) có 2 nghiệm dương phân biệt \Leftrightarrow \left\{ \begin{array}{l} \Delta > 0\\ - \frac{b}{a} > 0\\ \frac{c}{a} > 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 9 - 4m > 0\\ 3 > 0\\ m > 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m < \frac{9}{4}\\ m > 0 \end{array} \right.\,\, \Leftrightarrow 0 < m < \frac{9}{4}. Khi đó, gọi {{t}_{1}},\,\,{{t}_{2}}\,\,\,\left( 0<{{t}_{1}}<{{t}_{2}} \right) là nghiệm của phương trình \left( I \right). Suy ra \left( * \right) có bốn nghiệm theo thứ tự phân biệt là {{x}_{1}}=-\,\sqrt{{{t}_{2}}},\,\,{{x}_{2}}=-\,\sqrt{{{t}_{1}}},\,\,{{x}_{3}}=\sqrt{{{t}_{1}}},\,\,{{x}_{4}}=\sqrt{{{t}_{2}}}. Do tính đối xứng của \left( C \right) nên {{S}_{1}}={{S}_{2}} \begin{align} & \Leftrightarrow \,\int\limits_{0}^{{{x}_{3}}}{\left( {{x}^{4}}-3{{x}^{2}}+m \right)\,\text{d}x}=\int\limits_{{{x}_{3}}}^{{{x}_{4}}}{\left( -\,{{x}^{4}}+3{{x}^{2}}-m \right)\,\text{d}x} \\ & \left. \Leftrightarrow \left( \frac{{{x}^{5}}}{5}-{{x}^{3}}+mx \right) \right|_{0}^{{{x}_{3}}}=\left. \left( -\,\frac{{{x}^{5}}}{5}+{{x}^{3}}-mx \right) \right|_{{{x}_{3}}}^{{{x}_{4}}} \\ & \Leftrightarrow \frac{x_{3}^{5}}{5}-x_{3}^{3}+m{{x}_{3}}=-\frac{x_{4}^{5}}{5}+x_{4}^{3}-m{{x}_{4}}+\frac{x_{3}^{5}}{5}-x_{3}^{3}+m{{x}_{3}} \\ & \Leftrightarrow -\frac{x_{4}^{5}}{5}+x_{4}^{3}-m{{x}_{4}}=0. \\\end{align} Mà a={{x}_{4}} là nghiệm của phương trình \left( * \right) nên suy ra \left\{ \begin{array}{l} x_4^4 - 3x_4^2 + m = 0\\ - \,\frac{{x_4^5}}{5} + x_4^3 - m{x_4} = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m = - \,{a^4} + 3{a^2}\\ m = - \frac{{{a^4}}}{5} + {a^2} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m = - \,{a^4} + 3{a^2}\\ - \,{a^4} + 3{a^2} = - \,\frac{{{a^4}}}{5} + {a^2} \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m = - \,{a^4} + 3{a^2}\\ \left[ \begin{array}{l} {a^2} = 0\\ {a^2} = \frac{5}{2} \end{array} \right. \end{array} \right.\,\, \Rightarrow \,\,\left[ \begin{array}{l} m = 0\\ m = \frac{5}{4} \end{array} \right.. Kết hợp với điều kiện 0<m<\frac{9}{4}\,\,\xrightarrow{{}}\,\,m=\frac{5}{4} là giá trị cần tìm. Chọn D
Câu hỏi 44 : Trong mặt phẳng tọa độ Oxy, gọi \left( {{H_1}} \right) là hình phẳng giới hạn bởi các đường y = \frac{{{x^2}}}{4};\,\,y = - \frac{{{x^2}}}{4};\,\,x = - 4;\,\,x = 4 và \left( {{H_2}} \right) là hình gồm tất cả các điểm \left( {x;y} \right) thỏa {x^2} + {y^2} \le 16;\,\,{x^2} + {\left( {y - 2} \right)^2} \ge 4;\,\,{x^2} + {\left( {y + 2} \right)^2} \ge 4.
Cho \left( {{H_1}} \right) và \left( {{H_2}} \right) quanh quanh trục Oy ta được các vật thể có thể tích là {V_1},\,\,{V_2}. Đẳng thức nào sau đây đúng ?
Đáp án: B Phương pháp giải: Sử dụng các công thức tính thể tính khối trụ, khối cầu và ứng dụng tích phân để tính thể tích của vật thể tròn xoay. Lời giải chi tiết: {V_1} là thể tích khối trụ có bán kính đáy bằng 4 và chiều cao bằng 8 trừ đi bốn lần thể tích của vật thể tròn xoay tạo thành khi vật thể bị giới hạn bởi các đường x = 2\sqrt y ;\,\,x = 0;\,\,y = 0;\,\,x = 4 quay quanh trục Oy. \Rightarrow {V_1} = \pi {.4^2}.8 - 4\pi \int\limits_0^4 {2ydy} = 64\pi {V_2} là thể tích khối cầu có bán kính bằng 4 trừ đi 2 lần thể tích khối cầu có bán kính bằng 2. \Rightarrow {V_2} = \frac{4}{3}\pi \left( {{4^3} - {{2.2}^3}} \right) = 64\pi Vậy {V_1} = {V_2}. Chọn B. Câu hỏi 45 : Cho hai hàm số f\left( x \right) = a{x^3} + b{x^2} + cx - 1 và g\left( x \right) = d{x^2} + ex + \frac{1}{2}\,\,\left( {a,b,c,d,e \in R} \right). Biết rằng đồ thị của hàm số y = f\left( x \right) và y = g\left( x \right) cắt nhau tại ba điểm có hoành độ lần lượt là - 3; - 1;2 (tham khảo hình vẽ). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
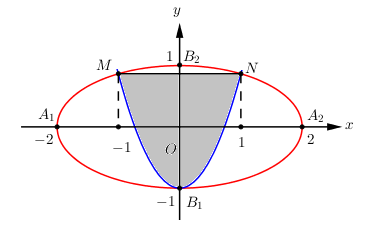
Đáp án: C Phương pháp giải: Diện tích hình phẳng giới hạn bởi các đường y = f\left( x \right);\,\,y = g\left( x \right);\,\,x = a;\,\,x = b là S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} Lời giải chi tiết: Xét phương trình hoành độ giao điểm \begin{array}{l}a{x^3} + b{x^2} + cx - 1 = d{x^2} + ex + \dfrac{1}{2}\\ \Leftrightarrow a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x - \dfrac{3}{2} = 0\end{array} Dễ thấy phương trình trên có 3 nghiệm phân biệt - 3; - 1;2 nên \begin{array}{l} \Leftrightarrow a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x - \dfrac{3}{2} = a\left( {x + 3} \right)\left( {x + 1} \right)\left( {x - 2} \right)\\ \Leftrightarrow a{x^3} + \left( {b - d} \right){x^2} + \left( {c - e} \right)x - \dfrac{3}{2} = a{x^3} + 2a{x^2} - 5ax + 6a\end{array} Đồng nhất hệ số ta được: - \dfrac{3}{2} = 6a \Leftrightarrow a = - \dfrac{1}{4} \Rightarrow f\left( x \right) - g\left( x \right) = - \dfrac{1}{4}\left( {x + 3} \right)\left( {x + 1} \right)\left( {x - 2} \right) \begin{array}{l} \Rightarrow S = \int\limits_{ - 3}^{ - 1} {\left| { - \dfrac{1}{4}\left( {x + 3} \right)\left( {x + 1} \right)\left( {x - 2} \right)} \right|dx} + \int\limits_{ - 1}^2 {\left| { - \dfrac{1}{4}\left( {x + 3} \right)\left( {x + 1} \right)\left( {x - 2} \right)} \right|dx} \\\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{4}.\dfrac{{16}}{3} + \dfrac{1}{4}.\dfrac{{63}}{4} = \dfrac{{253}}{{48}}\end{array} Chọn C. Câu hỏi 46 : Một biển quảng cáo có dạng hình elip với bốn đỉnh {A_1},\,{A_2},\,{B_1},\,{B_2} như hình vẽ bên. Người ta chia elip bởi parabol có đỉnh {B_1}, trục đối xứng {B_1}{B_2} và đi qua các điểm M,N . Sau đó sơn phần tô đậm với giá 200.000 đồng/{m^2} và trang trí phần đèn led còn lại với giá 500000 đồng/m^2. Hỏi kinh phí sử dụng gần nhất với giá trị nào dưới đây? Biết rằng {A_1}{A_2} = 4m,\,{B_1}{B_2} = 2m,\,MN = 2m.
Đáp án: A Phương pháp giải: +) Gắn trục tọa độ Oxy, xác định phương trình Elip và phương trình Parabol. +) Ứng dụng tích phân để tính diện tích phần tô đậm {S_1}. +) Tính diện tích phần không tô đậm: {S_2} = {S_{\left( E \right)}} - {S_1}. +) Tính kinh phí. Lời giải chi tiết: Gắn hệ trục tọa độ như hình vẽ.
Phương trình elip : \left( E \right):\,\,\dfrac{{{x^2}}}{4} + \dfrac{{{y^2}}}{1} = 1 \Leftrightarrow {x^2} + 4{y^2} = 4 \Leftrightarrow y = \pm \dfrac{{\sqrt {4 - {x^2}} }}{2}. Do MN = 2 \Rightarrow {x_N} = 1,\,\,{x_M} = - 1. Thay x = - 1 vào phương trình \left( E \right) \Rightarrow 1 + 4{y^2} = 4 \Leftrightarrow 4{y^2} = 3 \Leftrightarrow y = \dfrac{{ \pm \sqrt 3 }}{2} \Rightarrow M\left( { - 1;\dfrac{{\sqrt 3 }}{2}} \right). Thay x = 1 vào phương trình \left( E \right) \Rightarrow 1 + 4{y^2} = 4 \Leftrightarrow 4{y^2} = 3 \Leftrightarrow y = \dfrac{{ \pm \sqrt 3 }}{2} \Rightarrow N\left( {1;\dfrac{{\sqrt 3 }}{2}} \right). Gọi phương trình Parabol là y = a{x^2} + bx + c\,\,\left( P \right). \left( P \right) đi qua các điểm \left( {0; - 1} \right);\,\,\left( {1;\dfrac{{\sqrt 3 }}{2}} \right);\,\,\left( { - 1;\dfrac{{\sqrt 3 }}{2}} \right) nên ta có hệ phương trình: \left\{ \begin{array}{l}c = - 1\\a + b + c = \dfrac{{\sqrt 3 }}{2}\\a - b + c = \dfrac{{\sqrt 3 }}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = - 1\\a + c = \dfrac{{\sqrt 3 }}{2}\\b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{{\sqrt 3 }}{2} + 1\\b = 0\\c = - 1\end{array} \right. \Rightarrow \left( P \right):\,\,y = \left( {\dfrac{{\sqrt 3 }}{2} + 1} \right){x^2} - 1 Do đó diện tích phần tô đậm là {S_1} = \int\limits_{ - 1}^1 {\left( {\dfrac{{\sqrt {4 - {x^2}} }}{2} - \left( {\dfrac{{\sqrt 3 }}{2} + 1} \right){x^2} + 1} \right)dx} \approx 2,6692. Diện tích Elip là {S_E} = \pi ab = \pi .2.1 = 2\pi \Rightarrow Diện tích phần còn lại để trang trí đèn led là {S_2} = {S_{\left( E \right)}} - {S_1} \approx 3,6140. Vậy kinh phí là: 200\,\,000.{S_1} + 500\,\,000.{S_2} \approx 2\,\,340\,\,840 \approx 2\,\,341\,\,000 (đồng). Chọn A. Câu hỏi 47 : Người ta sử dụng xe bồn để chở dầu. Thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có độ dài trục lớn bằng 2m, độ dài trục bé bằng 1,6m, chiều dài (mặt trong của thùng) bằng 3,5m. Thùng được đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ điểm thấp nhất của đáy thùng đến mặt dầu) là 1,2m. Tính thể tích V của dầu có trong thùng (Kết quả làm tròn đến hàng phần trăm).
Đáp án: C Phương pháp giải: - Gắn hệ trục tọa độ lên mặt thiết diện ngang. Viết phương trình elip. - Tính diện tích phần thiết diện chỉ chứa dầu. - Tính thể tích phần dầu trong thùng, sử dụng công thức V = Sh với S là diện tích một phần elip tính được ở trên, h là chiều dài của thùng chứa dầu. Lời giải chi tiết: Chọn hệ trục tọa độ như hình vẽ. Phương trình elip \frac{{{x^2}}}{1} + \frac{{{y^2}}}{{0,{8^2}}} = 1 \Leftrightarrow y = \pm 0,8\sqrt {1 - {x^2}} . Diện tích thiết diện có chứa dầu là phần diện tích được gạch chéo trong hình. Ta tính diện tích phần không gạch chéo {S_1} là phần hình phẳng giới hạn bởi đường thẳng y = 0,4 với một phần elip phía trên trục hoành có phương trình y = 0,8\sqrt {1 - {x^2}} . Phương trình hoành độ giao điểm: 0,4 = 0,8\sqrt {1 - {x^2}} \Leftrightarrow x = \pm \frac{{\sqrt 3 }}{2}. Diện tích phần không gạch chéo: {S_1} = \int\limits_{ - \frac{{\sqrt 3 }}{2}}^{\frac{{\sqrt 3 }}{2}} {\left( {0,8\sqrt {1 - {x^2}} - 0,4} \right)dx} \approx 0,49\left( {{m^2}} \right). Diện tích elip: S = \pi ab = \pi .1.0,8 \approx 2,51\left( {{m^2}} \right). Diện tích phần gạch chéo: {S_2} = S - {S_1} = 2,51 - 0,49 = 2,02\left( {{m^2}} \right). Thể tích dầu là: V = {S_2}.h = 2,02.3,5 \approx 7,08\left( {{m^3}} \right). Chọn C. Câu hỏi 48 : Cho đường thẳng y = x và parabol y = \frac{1}{2}{x^2} + a (a là tham số thực dương). Gọi {S_1} và {S_2} lần lượt là diện tích của hai hình phẳng được tô màu trong hình vẽ bên. Khi {S_1} = {S_2} thì a thuộc khoảng nào dưới đây?
Đáp án: C Phương pháp giải: Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng x = a,\;x = b\;\;\left( {a < b} \right) và các đồ thị hàm số y = f\left( x \right),\;y = g\left( x \right) là: S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx.} Lời giải chi tiết: Xét phương trình hoành độ giao điểm của hai đồ thị hàm số ta có: \frac{1}{2}{x^2} + a = x \Leftrightarrow {x^2} - 2x + 2a = 0 \Leftrightarrow \left[ \begin{array}{l}{x_1} = 1 - \sqrt {1 - 2a} \\{x_2} = 1 + \sqrt {1 - 2a} \end{array} \right.\,\,\,\,\left( {a < \frac{1}{2}} \right). Đặt t = \sqrt {1 - 2a} \,\,\,\left( {t \ge 0} \right) \Rightarrow {t^2} = 1 - 2a \Leftrightarrow a = \frac{{1 - {t^2}}}{2}. Xét hàm số:g\left( x \right) = {x^2} - x + a và \int {g\left( x \right)dx} = G\left( x \right) + C. Theo giả thiết ta có: \left\{ \begin{array}{l}{S_1} = \int\limits_0^{{x_1}} {g\left( x \right)dx} = G\left( {{x_1}} \right) - G\left( 0 \right)\\{S_2} = - \int\limits_{{x_1}}^{{x_2}} {g\left( x \right)dx} = G\left( {{x_1}} \right) - G\left( {{x_2}} \right)\end{array} \right.. Lại có: {S_1} = {S_2} \Rightarrow G\left( {{x_2}} \right) = G\left( 0 \right) \Rightarrow \frac{1}{6}x_2^3 - \frac{1}{2}x_2^2 + a{x_2} = 0 \begin{array}{l} \Rightarrow x_2^2 - 3{x_2} + 6a = 0 \Rightarrow {\left( {1 + t} \right)^2} - 3\left( {1 + t} \right) + 6\left( {\frac{{1 - {t^2}}}{2}} \right) = 0\\ \Leftrightarrow {t^2} + 2t + 1 - 3t - 3 + 3 - 3{t^2} = 0\\ \Leftrightarrow - 2{t^2} - t + 1 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{2}\,\,\,\left( {tm} \right)\\t = - 1\,\,\,\left( {ktm} \right)\end{array} \right.\\ \Rightarrow a = \frac{{1 - \frac{1}{4}}}{2} = \frac{3}{8}\,\,\left( {tm} \right).\end{array} Chọn C. Câu hỏi 49 : Cho hàm số y = {x^4} - 3{x^2} + m có đồ thị là \left( {{C_m}} \right) (m là tham số thực). Giả sử \left( {{C_m}} \right) cắt trục Ox tại 4 điểm phân biệt. Gọi {S_1},\,\,{S_2} là diện tích của hai hình phẳng nằm dưới trục Ox và {S_3} là diện tích của hình phẳng nằm trên trục Ox được tạo bởi \left( {{C_m}} \right) với trục Ox. Biết rằng tồn tại duy nhất giá trị m = \dfrac{a}{b} (với a,\,\,b \in {\mathbb{N}^*} và tối giản) để {S_1} + {S_2} = {S_3}. Giá trị của 2a - b bằng:
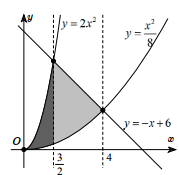
Đáp án: C Phương pháp giải: Lời giải chi tiết: Xét phương trình hoành độ giao điểm: {x^4} - 3{x^2} + m = 0\,\,\,\left( 1 \right). Đặt t = {x^2}\,\,\left( {t \ge 0} \right), khi đó phương trình (1) trở thành {t^2} - 3t + m = 0\,\,\,\left( 2 \right). Vì đồ thị hàm số y = {x^4} - 3{x^2} + m cắt trục hoành tại 4 điểm phân biệt nên phương trình (1) có 4 nghiệm phân biệt, do đó phương trình (2) phải có 2 nghiệm dương phân biệt. \Rightarrow \left\{ \begin{array}{l}\Delta > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}9 - 4m > 0\\3 > 0\,\,\left( {luon\,\,dung} \right)\\m > 0\end{array} \right. \Leftrightarrow 0 < m < \dfrac{9}{4}\,\,\,\left( * \right). Giả sử phương trình (2) có 2 nghiệm dương phân biệt 0 < {t_1} < {t_2}, áp dụng định lí Vi-ét ta có \left\{ \begin{array}{l}{t_1} + {t_2} = 3\\{t_1}{t_2} = m\end{array} \right.. Khi đó phương trình (1) có 4 nghiệm phân biệt - \sqrt {{t_2}} < - \sqrt {{t_1}} < \sqrt {{t_1}} < \sqrt {{t_2}} . Do tính đối xứng qua trục tung của hàm đa thức bậc bốn trùng phương nên {S_1} = {S_2}, do đó theo bài ra ta có {S_1} + {S_2} = {S_3} \Leftrightarrow 2{S_1} = {S_3}. Ta có: {S_2} = \int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {\left| {f\left( x \right)} \right|dx} = - \int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {f\left( x \right)dx} {S_3} = \int\limits_{ - \sqrt {{t_1}} }^{\sqrt {{t_1}} } {\left| {f\left( x \right)} \right|dx} = \int\limits_{ - \sqrt {{t_1}} }^{\sqrt {{t_1}} } {f\left( x \right)dx} = 2\int\limits_0^{\sqrt {{t_1}} } {f\left( x \right)dx} (do f\left( x \right) là hàm chẵn). Ta có: \begin{array}{l}2{S_2} = {S_3}\\ \Leftrightarrow - 2\int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {f\left( x \right)dx} = 2\int\limits_0^{\sqrt {{t_1}} } {f\left( x \right)dx} \\ \Leftrightarrow 2\left( {\int\limits_0^{\sqrt {{t_1}} } {f\left( x \right)dx} + \int\limits_{\sqrt {{t_1}} }^{\sqrt {{t_2}} } {f\left( x \right)dx} } \right) = 0\\ \Leftrightarrow 2\int\limits_0^{\sqrt {{t_2}} } {f\left( x \right)dx} = 0 \Leftrightarrow \int\limits_0^{\sqrt {{t_2}} } {f\left( x \right)dx} = 0\\ \Leftrightarrow \int\limits_0^{\sqrt {{t_2}} } {\left( {{x^4} - 3{x^2} + m} \right)dx} = 0\\ \Leftrightarrow \left. {\left( {\dfrac{{{x^5}}}{5} - {x^3} + mx} \right)} \right|_0^{\sqrt {{t_2}} } = 0\\ \Leftrightarrow \dfrac{{{{\left( {\sqrt {{t_2}} } \right)}^5}}}{5} - {\left( {\sqrt {{t_2}} } \right)^3} + m\sqrt {{t_2}} = 0\\ \Leftrightarrow \sqrt {{t_2}} \left( {\dfrac{{{t^2}}}{5} - t + m} \right) = 0\\ \Leftrightarrow \dfrac{{t_2^2}}{5} - {t_2} + m = 0\,\,\,\left( {Do\,\,{t_2} > 0} \right)\\ \Leftrightarrow t_2^2 - 5{t_2} + 5m = 0\,\,\left( * \right)\end{array} Mà {t_2} là nghiệm của phương trình {t^2} - 3t + m = 0 nên t_2^2 - 3{t_2} + m = 0 và {t_2} = \dfrac{{3 + \sqrt {9 - 4m} }}{2}. Do đó \begin{array}{l}\left( * \right) \Leftrightarrow t_2^2 - 3{t_2} + m - 2{t_2} + 4m = 0\\ \Leftrightarrow - 2{t_2} + 4m = 0 \Leftrightarrow {t_2} = 2m\end{array} \begin{array}{l} \Rightarrow \dfrac{{3 + \sqrt {9 - 4m} }}{2} = 2m\\ \Leftrightarrow 3 + \sqrt {9 - 4m} = 4m\\ \Leftrightarrow \sqrt {9 - 4m} = 4m - 3\\ \Leftrightarrow \left\{ \begin{array}{l}4m - 3 > 0\\9 - 4m = 16{m^2} - 24m + 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{3}{4}\\16{m^2} - 20m = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{3}{4}\\\left[ \begin{array}{l}m = 0\\m = \dfrac{5}{4}\end{array} \right.\end{array} \right. \Leftrightarrow m = \dfrac{5}{4}\,\,\left( {tm\,\,*} \right)\end{array} Vậy a = 5,\,\,b = 4 \Rightarrow 2a - b = 10 - 4 = 6. Chọn C. Câu hỏi 50 : Trong mặt phẳng tọa độ (Oxy) cho hình phẳng D giới hạn bởi các đường y = 2{x^2}, y = \dfrac{{{x^2}}}{8}, y = - x + 6. Tính diện tích hình phẳng D nằm bên phải của trục tung
Đáp án: C Phương pháp giải: - Giải các phương trình hoành độ giao điểm để xác định các cận. - Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f\left( x \right),\,\,y = g\left( x \right), đường thẳng x = a,\,\,x = b là: S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} . Lời giải chi tiết:
Xét các phương trình hoành độ giao điểm: \begin{array}{l}2{x^2} = \dfrac{{{x^2}}}{8} \Leftrightarrow x = 0\\2{x^2} = - x + 6 \Leftrightarrow x = \dfrac{3}{2}\,\,\left( {x \ge 0} \right)\\\dfrac{{{x^2}}}{8} = - x + 6 \Leftrightarrow x = 4\,\,\left( {x \ge 0} \right)\end{array} Vậy S = \int\limits_0^{\dfrac{3}{2}} {\left( {2{x^2} - \dfrac{{{x^2}}}{8}} \right)dx} + \int\limits_{\dfrac{3}{2}}^4 {\left( { - x + 6 - \dfrac{{{x^2}}}{8}} \right)dx} = \dfrac{{185}}{{24}}. Chọn C.
|