Phương pháp giải:

Gọi số phức \(z=a+bi\left( a,b\in R \right)\), thay vào điều kiện đề bài tìm \(a,b\Rightarrow z\Rightarrow w\).

Lời giải chi tiết:

Giả sử \(z = a + bi\left( {a,b \in R} \right)\)., ta có:

\(\begin{array}{l}z + 2 - 4i = \left( {2 - i} \right)\overline {iz} \\ \Rightarrow a + bi + 2 - 4i = (2 - i)\overline {i\left( {a + bi} \right)} \\ \Leftrightarrow a + 2 + (b - 4)i = (2 - i)( - b - ai)\\ \Leftrightarrow a + 2 + (b - 4)i =  - 2b - 2ai + bi - a\\ \Leftrightarrow \left\{ \begin{array}{l}a + 2 =  - a - 2b\\b - 4 =  - 2a + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a + 2b =  - 2\\2a = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - 3\end{array} \right.\end{array}\)

\(\Rightarrow z=2-3i\)

\(\Rightarrow \text{w}={{\left( 2-3i \right)}^{3}}-i=8-36i-54+27i-i=-46-10i\)

Vậy phần thực của số phức \(w\) là \(-46\)

Chọn A

Phương pháp giải:

Gọi số phức \(z=a+bi\left( a,b\in R \right)\), thay vào điều kiện đề bài tìm \(a,b\Rightarrow z\Rightarrow P\).

Lời giải chi tiết:

Giả sử \(z=a+bi\left( a,b\in R \right)\), ta có:

\(5\overline{z}+3-i=(-2+5i)z\)

\(\begin{array}{l} \Leftrightarrow 5(a - bi) + 3 - i = ( - 2 + 5i)(a + bi)\\ \Leftrightarrow 5a - 5bi + 3 - i =  - 2a - 2bi + 5ai - 5b\end{array}\)

\( \Leftrightarrow \left\{ \begin{array}{l}5a + 3 =  - 2a - 5b\\ - 5b - 1 = 5a - 2b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}7a + 5b =  - 3\\5a + 3b =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 2\end{array} \right.\)

\(\Rightarrow z=1-2i\)

\(\Rightarrow P=\left| 3i{{\left( z-1 \right)}^{2}} \right|=\left| 3i{{(1-2i-1)}^{2}} \right|=\left| -12i \right|=12\)

Chọn B

Phương pháp giải:

Đặt \(z = a + bi \Rightarrow \overline z  = a - bi\). Thay vào giả thiết tìm a, b.

Lời giải chi tiết:

Đặt \(z = a + bi \Rightarrow \overline z  = a - bi\) ta có:

\(\begin{array}{l}2i\left( {a + bi} \right) + 3\left( {a - bi} \right) = 5 \Leftrightarrow 2ai - 2b + 3a - 3bi = 5\\ \Leftrightarrow \left\{ \begin{array}{l} - 2b + 3a = 5\\2a - 3b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = 2\end{array} \right. \Rightarrow z = 3 + 2i\end{array}\)

Chọn D

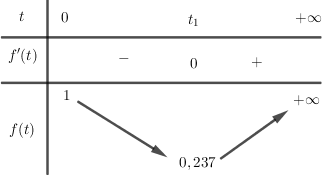
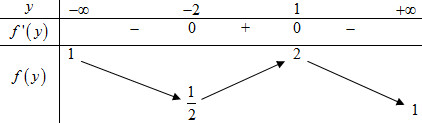
Phương pháp giải:

+) Đặt \(t = \left| z \right|\), rút \(z\) từ đẳng thức bài cho theo \(t\) .

+) Lấy môđun hai vế đưa về phương trình ẩn \(t\).

+) Giải phương trình ẩn \(t\) và kết luận.

Lời giải chi tiết:

Đặt \(t = \left| z \right| \ge 0\) ta có : \(\left( {1 + i} \right)zt - 1 = \left( {i - 2} \right)t\)

\(\begin{array}{l} \Rightarrow \left( {1 + i} \right)zt = 1 + \left( {i - 2} \right)t \Rightarrow \left| {1 + i} \right|.\left| z \right|.t = \left| {1 - 2t + ti} \right|\\ \Rightarrow \sqrt 2 {t^2} = \sqrt {{{\left( {1 - 2t} \right)}^2} + {t^2}}  \Leftrightarrow 2{t^4} = 1 - 4t + 4{t^2} + {t^2}\\ \Leftrightarrow 2{t^4} - 5{t^2} + 4t - 1 = 0 \Leftrightarrow \left( {t - 1} \right)\left( {2{t^3} + 2{t^2} - 3t + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t = 1\\2{t^3} + 2{t^2} - 3t + 1 = 0\end{array} \right.\end{array}\)

Xét hàm \(f\left( t \right) = 2{t^3} + 2{t^2} - 3t + 1\) trên \(\left[ {0; + \infty } \right)\) có:

\(f'\left( t \right) = 6{t^2} + 4t - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{{ - 2 + \sqrt {22} }}{6} = {t_1} > 0\\t = \dfrac{{ - 2 - \sqrt {22} }}{6} < 0\left( L \right)\end{array} \right.\)

Bảng biến thiên:

Từ bảng biến thiên ta thấy \(f\left( t \right) > 0,\forall t \ge 0\) nên phương trình \(f\left( t \right) = 0\) vô nghiệm.

Vậy \(t = 1\) hay \(\left| z \right| = 1\).

Chọn A

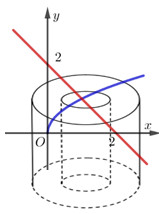
Phương pháp giải:

+) \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \).

+) \(w = x + yi\) là số thực \( \Leftrightarrow y = 0\).

Lời giải chi tiết:

\(\left| z \right| = 5 \Leftrightarrow {a^2} + {b^2} = 25\).

Ta có: \(z\left( {2 + i} \right)\left( {1 - 2i} \right) = \left( {a + bi} \right)\left( {4 - 3i} \right) = 4a + 3b + \left( { - 3a + 4b} \right)i\) là số thực \( \Rightarrow  - 3a + 4b = 0\).

Từ đó ta có hệ phương trình

\(\begin{array}{l}\left\{ \begin{array}{l}{a^2} + {b^2} = 25\\ - 3a + 4b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} + \dfrac{9}{{16}}{a^2} = 25\\b = \dfrac{{3a}}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{25}}{{16}}{a^2} = 25\\b = \dfrac{{3a}}{4}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{a^2} = 16\\b = \dfrac{{3a}}{4}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 4,\,\,b = 3\\a =  - 4;\,\,b =  - 3\end{array} \right. \Rightarrow P = \left| a \right| + \left| b \right| = 4 + 3 = 7\end{array}\)

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

Chọn D.

Phương pháp giải:

+) Gọi \(z = x + yi\,\,\,\left( {x;y \in \mathbb{R}} \right)\) thì số phức liên hợp \(\overline z  = x - yi\) và mô đun \(\left| z \right| = \sqrt {{x^2} + {y^2}} \)

+) Biến đổi giả thiết để đưa về hai số phức bằng nhau thì phần thực bằng nhau và phần ảo bằng nhau.

Lời giải chi tiết:

Gọi \(z = x + yi\,\,\,\left( {x;y \in \mathbb{R}} \right)\) thì số phức liên hợp \(\overline z  = x - yi\)

Ta có \(\overline z  + \left( {1 - i} \right)z = 9 - 2i \Leftrightarrow x - yi + \left( {1 - i} \right)\left( {x + yi} \right) = 9 - 2i\)

\( \Leftrightarrow x - yi + x + y + yi - xi = 9 - 2i \Leftrightarrow 2x + y - xi = 9 - 2i\)

\( \Leftrightarrow \left\{ \begin{array}{l}2x + y = 9\\ - x =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 5\end{array} \right.\). Suy ra \(z = 2 + 5i \Rightarrow \left| z \right| = \sqrt {{2^2} + {5^2}}  = \sqrt {29} .\)

Chọn D.

Phương pháp giải:

- Thay \(z,\overline z \) vào điều kiện bài toán, sử dụng định nghĩa hai số phức bằng nhau suy ra hệ phương trình ẩn \(a,b\)

- Giải hệ phương trình tìm \(a,b\) và kết luận.

Lời giải chi tiết:

Ta có : \(z = a + bi \Rightarrow \overline z  = a - bi\).

Thay vào điều kiện bài cho ta được : \(\left( {a + bi} \right) - \left( {2 + 3i} \right)\left( {a - bi} \right) = 1 - 9i\)

\(\begin{array}{l} \Leftrightarrow a + bi - \left( {2a + 3b + \left( {3a - 2b} \right)i} \right) = 1 - 9i \Leftrightarrow a + bi - \left( {2a + 3b} \right) - \left( {3a - 2b} \right)i = 1 - 9i\\ \Leftrightarrow \left( { - a - 3b} \right) + \left( {3b - 3a} \right)i = 1 - 9i \Leftrightarrow \left\{ \begin{array}{l} - a - 3b = 1\\3b - 3a =  - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - 1\end{array} \right.\\ \Rightarrow T = ab + 1 = 2.\left( { - 1} \right) + 1 =  - 1\end{array}\) 

Chọn D.

Phương pháp giải:

+) Đặt \(z = a + bi\), giải phương trình tìm \(z\).

+) \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \).

Lời giải chi tiết:

Đặt \(z = a + bi\,\,\left( {a;b \in \mathbb{R}} \right) \Rightarrow \overline z  = a - bi\).

Theo bài ra ta có: \(\left( {2 - i} \right)z + 3 + 16i = 2\left( {\overline z  + i} \right).\)

\(\begin{array}{l} \Leftrightarrow \left( {2 - i} \right)\left( {a + bi} \right) + 3 + 16i = 2\left( {a - bi + i} \right)\\ \Leftrightarrow 2a + 2bi - ai + b + 3 + 16i = 2a - 2bi + 2i\\ \Leftrightarrow \left\{ \begin{array}{l}2a + b + 3 = 2a\\2b - a + 16 =  - 2b + 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 3\\4b - a =  - 14\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 3\\a = 2\end{array} \right.\\ \Rightarrow z = 2 - 3i \Rightarrow \left| z \right| = \sqrt {{2^2} + {{\left( { - 3} \right)}^2}}  = \sqrt {13} \end{array}\)

Chọn C

Phương pháp giải:

- \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \), suy ra mối liên hệ giữa \(a\) và \(b\).

- Thay \(z = a + bi\) vào \(\left( {4 - 3i} \right)z\), tìm phần ảo của nó và cho bằng 0, giải phương trình tìm \(\left| b \right|\).

- Thế ngược lại tìm \(\left| a \right|\) và tính \(\left| a \right| + \left| b \right| + 3.\)

Lời giải chi tiết:

Đặt \(z = a + bi\).

Ta có \(\left| z \right| = 5 \Rightarrow {a^2} + {b^2} = 25\) (1).

Lại có \(\left( {4 - 3i} \right)z = \left( {4 - 3i} \right)\left( {a + bi} \right)\)\( = 4a + 3b + \left( {4b - 3a} \right)i\)  là số thực nên \(4b = 3a \Leftrightarrow a = \dfrac{{4b}}{3}\).

Thay vào (1) ta có: \(\dfrac{{16{b^2}}}{9} + {b^2} = 25 \Leftrightarrow {b^2} = 9 \Leftrightarrow \left| b \right| = 3\).

 Với \({b^2} = 9\) ta có \({a^2} = 25 - {b^2} = 16\)\( \Rightarrow \left| a \right| = 4\).

Vậy \(\left| a \right| + \left| b \right| + 3 = 4 + 3 + 3 = 10.\)

Chọn B.

Phương pháp giải:

- Hai số phức bằng nhau: \({z_1} = {x_1} + {y_1}i,\,\,{z_2} = {x_2} + {y_2}i\).

\({z_1} = {z_2} \Leftrightarrow \left\{ \begin{array}{l}{x_1} = {x_2}\\{y_1} = {y_2}\end{array} \right.\)

- Giải hệ phương trình bằng MTCT tìm \(x,\,\,y\).

Lời giải chi tiết:

Ta có

\(\begin{array}{l}2x - \left( {3 - y} \right)i = y + 4 + \left( {x + y - 2} \right)i\\ \Leftrightarrow \left\{ \begin{array}{l}2x = y + 4\\y - 3 = x + y - 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2x - y = 4\\x = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 2\end{array} \right.\end{array}\)

Chọn A.

Phương pháp giải:

- Đặt \(z = x + yi \Rightarrow \overline z  = x - yi\).

- Thay vào giả thiết, đưa phương trình về dạng hai số phức bằng nhau.

- Hai số phức bằng nhau khi và chỉ khi chúng có phần thực bằng nhau và phần ảo bằng nhau.

- Giải hệ phương trình tìm \(x,\,\,y\).

Lời giải chi tiết:

Đặt \(z = x + yi \Rightarrow \overline z  = x - yi\). Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\,z + 2\overline z  = {\left( {1 + 5i} \right)^2}\\ \Leftrightarrow x + yi + 2\left( {x - yi} \right) =  - 24 + 10i\\ \Leftrightarrow 3x - yi =  - 24 + 10\\ \Rightarrow \left\{ \begin{array}{l}3x =  - 24\\ - y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 8\\y =  - 10\end{array} \right.\end{array}\)

Vậy \(z =  - 8 - 10i\) có phần ảo bằng \( - 10\).

Chọn C.

Phương pháp giải:

Đặt \(z = a + bi\), xét từng mệnh đề.

Lời giải chi tiết:

+) Đặt \(z = a + bi \Rightarrow  - z =  - a - bi.\)

Ta có: \(\left| z \right| = \sqrt {{a^2} + {b^2}} ,\,\,\left| { - z} \right| = \sqrt {{{\left( { - a} \right)}^2} + {{\left( { - b} \right)}^2}} \) \( \Rightarrow \left| z \right| = \left| { - z} \right|\) là mệnh đề đúng.

+) Đặt \(z = a + bi \Rightarrow \overline z  = a - bi.\)

Ta có: \(\left| z \right| = \sqrt {{a^2} + {b^2}} ,\,\,\left| {\overline z } \right| = \sqrt {{a^2} + {{\left( { - b} \right)}^2}} \) \( \Rightarrow \left| z \right| = \left| {\overline z } \right|\) là mệnh đề đúng.

+) Đặt \(z = a + bi \Rightarrow \overline z  = a - bi \Rightarrow z + \overline z  = 2a\)

\( \Rightarrow \left| {z + \overline z } \right| = \left| {2a} \right|\)\( \Rightarrow \left| {z + \overline z } \right| = 0\) là mệnh đề sai.

+) Đặt \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}}  \ge 0\)\( \Rightarrow \left| z \right| > 0\) là mệnh đề sai.

Vậy có 2 mệnh đề đúng.

Chọn A.

Phương pháp giải:

- Đặt ẩn \(z = a + bi\), rút a  theo b rồi tính.

- Tính \(\left| z \right| = \sqrt {{a^2} + {b^2}} \), thế \(a\) theo \(b\) và tìm GTNN bằng cách đưa biểu thức về dạng hằng đẳng thức.

Lời giải chi tiết:

Đặt \(z = a + bi\,\,\left( {a,\,\,b \in \mathbb{R}} \right)\)

Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,\left| {iz - 3} \right| = \left| {z - 2 - i} \right|\\ \Leftrightarrow \left| {i\left( {a + bi} \right) - 3} \right| = \left| {a + bi - 2 - i} \right|\\ \Leftrightarrow \left| {\left( { - 3 - b} \right) + ai} \right| = \left| {\left( {a - 2} \right) + \left( {b - 1} \right)i} \right|\\ \Leftrightarrow {\left( {b + 3} \right)^2} + {a^2} = {\left( {a - 2} \right)^2} + {\left( {b - 1} \right)^2}\\ \Leftrightarrow {b^2} + 6b + 9 + {a^2} = {a^2} - 4a + 4 + {b^2} - 2b + 1\\ \Leftrightarrow 4a + 8b + 4 = 0\\ \Leftrightarrow a + 2b + 1 = 0\\ \Leftrightarrow a =  - 2b - 1\end{array}\)

Ta có:

\(\begin{array}{l}\left| z \right| = \sqrt {{a^2} + {b^2}}  = \sqrt {{{\left( {2b + 1} \right)}^2} + {b^2}} \\\,\,\,\,\,\, = \sqrt {5{b^2} + 4b + 1}  = \sqrt {5\left( {{b^2} + \dfrac{4}{5}b} \right) + 1} \\\,\,\,\,\,\, = \sqrt {5\left( {{b^2} + 2.b.\dfrac{2}{5} + \dfrac{4}{{25}}} \right) - \dfrac{4}{5} + 1} \\\,\,\,\,\,\, = \sqrt {5{{\left( {b + \dfrac{2}{5}} \right)}^2} + \dfrac{1}{5}}  \ge \dfrac{{\sqrt 5 }}{5}\end{array}\)

Dấu bằng xảy ra khi và chỉ khi \(b =  - \dfrac{2}{5} \Rightarrow a =  - \dfrac{1}{5}.\)

Vậy \({\mathop{\rm Re}\nolimits} z = a =  - \dfrac{1}{5}\).

Chọn D.

Phương pháp giải:

- Số phức là một số thực khi nó có phần ảo bằng 0. Từ đó tìm \(m\) và suy ra số phức \(z\).

- Thay số phức \(z\) tìm được tính giá trị biểu thức đề  bài yêu cầu.

Lời giải chi tiết:

Vì \(z = {m^2} - 3m + 3 + \left( {m - 2} \right)i\) là số thực nên \(m - 2 = 0 \Leftrightarrow m = 2.\)

Suy ra \(z = {m^2} - 3m + 3 = 1.\)

Vậy \(1 + z + {z^2} + ... + {z^{2019}} = 1 + 1 + 1 + ... + 1 = 2020\) (có 2020 số 1).

Chon D.

Phương pháp giải:

Đặt \(z = a + bi\) rồi thay vào đề bài để tìm nghiệm.

Lời giải chi tiết:

Đặt \(z = a + bi\)\( \Rightarrow \overline\( \Leftrightarrow {\left( {a - 2} \right)^2} + {\left( {b - 2} \right)^2} = {\left( {a - 1} \right)^2} + {\left( {b - 1} \right)^2}\) z  = a - bi;{\left| z \right|^2} = {a^2} + {b^2}\)

Ta có \({\left| z \right|^2} = 2\left| {z - \overline z } \right| \Rightarrow {a^2} + {b^2} = 4{b^2} \Leftrightarrow {a^2} = 3{b^2}\)

+) \(\left| {z - 2 - 2i} \right| = \left| {z - 1 - i} \right|\)

\({\left( {3 - b} \right)^2} = 3{b^2} \Leftrightarrow 2{b^2} + 6b - 9 = 0 \Rightarrow \)

\( \Rightarrow a + b = 3 \Rightarrow a = 3 - b\)

Khi đó  có 2 nghiệm phân biệt nên có 2 số phức thỏa mãn.

Chọn A.

Phương pháp giải:

Gọi số phức \(z=a+bi\left( a,b\in R \right)\), thay vào điều kiện đề bài tìm mối liên hệ \(a,b\).

Tìm GTNN của \(\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\Rightarrow a,b\)

Lời giải chi tiết:

Giả sử \(z=a+bi\left( a,b\in R \right)\), ta có:

\(\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\)

\(\left| \overline{z}-3+4i \right|=\left| a-bi-3+4i \right|=\left| a-3+(4-b)i \right|=\sqrt{{{\left( a-3 \right)}^{2}}+{{\left( 4-b \right)}^{2}}}\)

\(\begin{array}{l} \Rightarrow \left| z \right| = \left| {\overline z  - 3 + 4i} \right|\\ \Leftrightarrow \sqrt {{a^2} + {b^2}}  = \sqrt {{{\left( {a - 3} \right)}^2} + {{\left( {4 - b}\right)}^2}} \\ \Leftrightarrow {a^2} + {b^2} = {a^2} - 6a + 9 + {b^2} - 8b + 16\end{array}\)

\(\Leftrightarrow 6a+8b=25\Leftrightarrow b=\frac{25-6a}{8}(1)\)

Xét \(\sqrt{{{a}^{2}}+{{b}^{2}}}=\sqrt{{{a}^{2}}+{{\left( \frac{25-6a}{8}\right)}^{2}}}=\sqrt{\frac{100{{a}^{2}}-300a+625}{64}}=\sqrt{\frac{{{\left( 10a-15\right)}^{2}}+400}{64}}\ge \frac{5}{2}\)

Dấu “=” xảy ra \(\Leftrightarrow 10a-15=0\Leftrightarrow a=\frac{3}{2}\)

Thay vào (1) ta được \(b=2\)

Vậy số phức \(z\) có mô đun nhỏ nhất thỏa mãn điều kiện bài toán là \(z=\frac{3}{2}+2i\)

Chọn D

Phương pháp giải:

- Đặt \(z = a + bi \Rightarrow \overline z  = a - bi\). Thay vào phương trình.

- Sử dụng điều kiện để hai số phức bằng nhau.

Lời giải chi tiết:

Ta có \(z = a + bi \Rightarrow \overline z  = a - bi\)

Khi đó

\(\begin{array}{l}\left( {1 + 2i} \right)z + \left( {3 - 4i} \right)\overline z  =  - 42 - 54i\\ \Leftrightarrow \left( {1 + 2i} \right)\left( {a + bi} \right) + \left( {3 - 4i} \right)\left( {a - bi} \right) =  - 42 - 54i\\ \Leftrightarrow \left( {4a - 6b} \right) + \left( { - 2a - 2b} \right)i =  - 42 - 54i\\ \Rightarrow \left\{ \begin{array}{l}4a - 6b =  - 42\\ - 2a - 2b =  - 54\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 12\\b = 15\end{array} \right.\\ \Rightarrow a + b = 27\end{array}\)

Chọn A.

Phương pháp giải:

- Đặt \(z = a + bi\). Thay vào biểu thức.

- Sử dụng công thức tính môđun của số phức.

- Một số phức là số thực khi và chỉ khi có phần ảo bằng 0.

- Rút a theo b hoặc ngược lại, sau đó giải phương trình tìm a, b.

Lời giải chi tiết:

Đặt \(z = a + bi\)

Ta có \(\left| {z + 2 - i} \right| = 2\sqrt 2  \Rightarrow {\left( {a + 2} \right)^2} + {\left( {b - 1} \right)^2} = 8\)  (*)

Mặt khác \({\left( {z - i} \right)^2} = {\left( {a + bi - i} \right)^2} = {a^2} - {\left( {b - 1} \right)^2} + 2a\left( {b - 1} \right)\) là một số thực nên \({a^2} - {\left( {b - 1} \right)^2} = 0\)\( \Leftrightarrow {a^2} = {\left( {b - 1} \right)^2}.\)

Khi đó ta có: \({\left( {a + 2} \right)^2} + {a^2} = 8 \Leftrightarrow 2{a^2} + 4a - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}a =  - 1 + \sqrt 3 \\a =  - 1 - \sqrt 3 \end{array} \right..\)

Vậy có 2 số phức z thỏa mãn yêu cầu bài toán.

Chọn A.

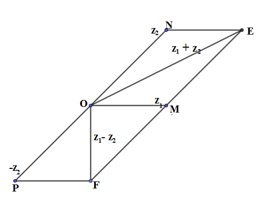
Phương pháp giải:

Áp dụng quy tắc hình bình hành.

Lời giải chi tiết:

Ta có \(M,N\) là điểm biểu diễn của \({z_1};i{z_2}\) nên \(OM = \left| {{z_1}} \right| = 6;ON = \left| {i{z_2}} \right| = 2\)

Trên tia ON lấy điểm K sao cho \(OK = 3ON = 6\) hay K là điểm biểu diễn của số phức \(3i{z_2}\).

Lấy điểm H sao cho \(OMHK\) là hình bình hành.

\( \Rightarrow \overrightarrow {OH}  = \overrightarrow {OM}  + \overrightarrow {ON}  \Rightarrow O{H^2} = O{M^2} + O{N^2} + 2OM.ON.\cos 60 \Rightarrow OH = 6\sqrt 3 \)

Mặt khác \(T = \left| {z_1^2 + 9z_2^2} \right| = \left| {z_1^2 - 9{{\left( {i{z_2}} \right)}^2}} \right| = \left| {{z_1} - 3i{z_2}} \right|.\left| {{z_1} + 3i{z_2}} \right| = MK.OH\)\( = 6.6\sqrt 3  = 36\sqrt 3 \)

Chọn B.

Phương pháp giải:

- Đặt \(z = a + bi \Rightarrow \overline z  = a - bi\), thay vào dữ kiện để tìm a, b.

- Số phức bằng 0 khi và chỉ khi nó có phần thực và phần ảo cùng bằng 0.

Lời giải chi tiết:

Đặt \(z = a + bi \Rightarrow \overline z  = a - bi.\)

Khi đó ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,{z^2} + 2\overline z  = 0\\ \Leftrightarrow {\left( {a + bi} \right)^2} + 2\left( {a - bi} \right) = 0\\ \Leftrightarrow {a^2} + 2abi + {b^2}{i^2} + 2a - 2bi = 0\\ \Leftrightarrow {a^2} - {b^2} + 2a + \left( {2ab - 2b} \right)i = 0\\ \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} + 2a = 0\\2ab - 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} + 2a = 0\\2b\left( {a - 1} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} + 2a = 0\\\left[ \begin{array}{l}b = 0\\a = 1\end{array} \right.\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = 1\\{b^2} + 3 = 0\,\,\left( {VN} \right)\end{array} \right.\\\left\{ \begin{array}{l}b = 0\\{a^2} + 2a = 0\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 0\\\left[ \begin{array}{l}a = 0\\a =  - 2\end{array} \right.\end{array} \right.\end{array}\)

Vậy có 2 số phức thỏa mãn yêu cầu bài toán là \(z = 0\) và \(z =  - 2\).

Chọn C.

Phương pháp giải:

- Tìm mô đun của số phức \(z - 2i\).

- Giải bất phương trình \(\left| {z - 2i} \right| > 1\) bằng phương pháp bình phương 2 vế.

Lời giải chi tiết:

Ta có \(z = m + 1 + mi \Rightarrow z - 2i = m + 1 + \left( {m - 2} \right)i.\)

\( \Rightarrow \left| {z - 2i} \right| = \sqrt {{{\left( {m + 1} \right)}^2} + {{\left( {m - 2} \right)}^2}} \).

Theo bài ra ta có: \(\left| {z - 2i} \right| > 1 \Rightarrow {\left( {m + 1} \right)^2} + {\left( {m - 2} \right)^2} > 1\)

\( \Leftrightarrow {m^2} + 2m + 1 + {m^2} - 4m + 4 > 1\) \( \Leftrightarrow 2{m^2} - 2m + 4 > 0\) (luôn đúng)

\( \Rightarrow m \in \mathbb{R}\).

Kết hợp điều kiện bài toán, ta có \(m \in \left( { - 5;5} \right),\,\,m \in \mathbb{Z}\)\( \Rightarrow m \in \left\{ { - 4; - 3; - 2; - 1;0;1;2;3;4} \right\}.\)

Vậy có 9 giá trị của m thỏa mãn yêu cầu bài toán.

Chọn D.

Phương pháp giải:

- Thay \(z = 1 + i\) vào phương trình.

- Một số phức bằng 0 khi và chỉ khi nó có phần thực và phần ảo cùng bằng 0.

- Giải hệ phương trình tìm a, b.

Lời giải chi tiết:

Vì \(z = 1 + i\) là 1 nghiệm của phương trình \(zi + azi + bz + a = 0\,\,\,\left( {a,b \in \mathbb{R}} \right)\) nên ta có:

\(\begin{array}{l}\,\,\,\,\,\,\left( {1 + i} \right)i + a.\left( {i + 1} \right)i + b\left( {i + 1} \right) + a = 0\\ \Leftrightarrow  - 1 + i + a\left( { - 1 + i} \right) + b + bi + a = 0\\ \Leftrightarrow b - 1 + \left( {1 + a + b} \right)i = 0\\ \Leftrightarrow \left\{ \begin{array}{l}b - 1 = 0\\1 + a + b = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}b = 1\\a =  - 2\end{array} \right.\end{array}\)

Vậy \({b^2} - {a^3} = {1^2} - {\left( { - 2} \right)^3} = 9.\)

Chọn D.

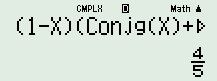
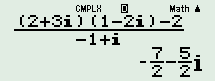
Phương pháp giải:

Cách 1:

- Đặt \(z = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\), thay vào biểu thức \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\), tìm điều kiện để \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực, tức là \({\mathop{\rm Im}\nolimits} \left( {1 - z} \right)\left( {\bar z + 2i} \right) = 0\), biểu diễn \(y\) theo \(x\).

- Tính \(\left| z \right| = \sqrt {{x^2} + {y^2}} \), thế \(y\) theo \(x\) tìm được ở trên, tìm GTNN của biểu thức dạng \(a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\), biểu thức đạt GTNN tại \(x =  - \dfrac{b}{{2a}}\) với \(a > 0\).

Cách 2:

- Tính môđun cả 4 số phức ở 4 đáp án, thử từ số phức có môđun nhỏ nhất.

- Thay lần lượt các số phức ở các đáp án vào biểu thức \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\), tìm số phức thỏa mãn \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực.

Lời giải chi tiết:

Cách 1:

Gọi \(z = x + yi\,\,\left( {x,\,\,y \in \mathbb{R}} \right)\), theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\left( {1 - z} \right)\left( {\bar z + 2i} \right)\\ = \left( {1 - x - yi} \right)\left( {x - yi + 2i} \right)\\ = \left( {1 - x - yi} \right)\left( {x - \left( {y - 2} \right)i} \right)\\ = \left( {1 - x} \right)x - \left( {1 - x} \right)\left( {y - 2} \right)i - xyi - y\left( {y - 2} \right)\\ = \left[ {\left( {1 - x} \right)x - y\left( {y - 2} \right)} \right] - \left[ {\left( {1 - x} \right)\left( {y - 2} \right) + xy} \right]i\end{array}\)

Để \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) là số thực thì \({\mathop{\rm Im}\nolimits} \left( {1 - z} \right)\left( {\bar z + 2i} \right) = 0\)

\(\begin{array}{l} \Leftrightarrow \left( {1 - x} \right)\left( {y - 2} \right) + xy = 0\\ \Leftrightarrow y - 2 - xy + 2x + xy = 0\\ \Leftrightarrow y = 2 - 2x\end{array}\)

Khi đó ta có: \({\left| z \right|^2} = {x^2} + {y^2} = {x^2} + {\left( {2 - 2x} \right)^2} = 5{x^2} - 8x + 4\).

 \( \Rightarrow {\left| z \right|_{\min }} \Leftrightarrow {\left| z \right|^2}_{\min } \Leftrightarrow x = \dfrac{8}{{2.5}} = \dfrac{4}{5}\), khi đó \(y = 2 - 2.\dfrac{4}{5} = \dfrac{2}{5}\).

Vậy số phức \(z\) thỏa mãn yêu cầu bài toán là: .\(z = \dfrac{4}{5} + \dfrac{2}{5}i\).

Cách 2:

Tính môđun tất cả các số phức ở các đáp án:

\(z = 1 + \dfrac{1}{2}i \Rightarrow \left| z \right| = \dfrac{{\sqrt 5 }}{2}\)

\(z = \dfrac{3}{5} + \dfrac{4}{5}i \Rightarrow \left| z \right| = 1\)

\(z = 2i \Rightarrow \left| z \right| = 2\)

\(z = \dfrac{4}{5} + \dfrac{2}{5}i \Rightarrow \left| z \right| = \dfrac{{2\sqrt 5 }}{5}\).

Thử từ số phức có môđun nhỏ nhất.

Xét đáp án D, thay số phức \(z = \dfrac{4}{5} + \dfrac{2}{5}i\) vào biểu thức \(\left( {1 - z} \right)\left( {\bar z + 2i} \right)\) (sử dụng MTCT):

là số thực, thỏa mãn.Vậy số phức \(z = \dfrac{4}{5} + \dfrac{2}{5}i\) thỏa mãn yêu cầu bài toán.

Chọn D.

Phương pháp giải:

Gọi số phức \(z=a+bi\left( a,b\in R \right)\), thay vào điều kiện đề bài tìm \(a,b\).

Công thức mô đun của số phức \(\left| z \right|=\sqrt{{{a}^{2}}+{{b}^{2}}}\).

Lời giải chi tiết:

Giả sử \(z=a+bi\left( a,b\in R \right)\), ta có:

\(\left| z \right|=2\Leftrightarrow \sqrt{{{a}^{2}}+{{b}^{2}}}=2\Leftrightarrow {{a}^{2}}+{{b}^{2}}=4(1)\)

\({{z}^{2}}+\overline{z}={{\left( a+bi \right)}^{2}}+a-bi={{a}^{2}}+2abi-{{b}^{2}}+a-bi=({{a}^{2}}+a-{{b}^{2}})+(2ab-b)i\)

\(\Rightarrow \left| {{z}^{2}}+\overline{z} \right|=2\Leftrightarrow {{\left|{{z}^{2}}+\overline{z} \right|}^{2}}=4\)

\(\begin{array}{l} \Leftrightarrow {\left( {{a^2} + a - {b^2}} \right)^2} + {\left( {2ab - b} \right)^2} = 4\\ \Leftrightarrow {a^4} + {a^2} + {b^4} + 2{a^3} - 2{a^2}{b^2} - 2a{b^2} +4{a^2}{b^2} + {b^2} - 4a{b^2} = 4\\ \Leftrightarrow {a^4} + {b^4} + 2{a^2}{b^2} + 2{a^3} - 6a{b^2} + {a^2} + {b^2} = 4\\ \Leftrightarrow {\left( {{a^2} + {b^2}} \right)^2} + 2a\left({{a^2} - 3{b^2}} \right) + ({a^2} + {b^2}) = 4(2)\end{array}\)

Thay (1) vào (2) ta được:

\(\begin{array}{l}16 + 2a(4 - 4{b^2}) + 4 = 4\\ \Leftrightarrow 2 + a\left( {1 - {b^2}} \right) = 0\\ \Leftrightarrow {b^2} = \frac{{2 + a}}{a}(3)\end{array}\)

Thay (3) vào (1) ta được: \({{a}^{2}}+\frac{2+a}{a}=4\Leftrightarrow {{a}^{3}}-3a+2=0\Leftrightarrow\left[ \begin{align}  & a=1 \\  & a=-2 \\ \end{align} \right.\)

Với \(a=-2\Rightarrow b=0\Rightarrow z=-2.\)

Với \(a=1\Rightarrow {{b}^{2}}=3\Rightarrow b=\pm \sqrt{3}\Rightarrow z=1\pm \sqrt{3}i.\)

Vậy có \(3\)  số phức \(z\) thỏa mãn điều kiện đề bài.

Chọn C.

Phương pháp giải:

Chia cả 2 vế cho \(\left| 1+i \right|\) và suy ra đường biểu diễn của số phức z.

Lời giải chi tiết:

\(\left| \left( 1+i \right)z+2 \right|+\left| \left( 1+i \right)z-2 \right|=4\sqrt{2}\Leftrightarrow \left| z+\frac{2}{1+i} \right|+\left| z-\frac{2}{1+i} \right|=\frac{4\sqrt{2}}{\left| 1+i \right|}\Leftrightarrow \left| z+1-i \right|+\left| z-1+i \right|=4\)

\(\Rightarrow \) Tập hợp các điểm z là elip có độ dài trục lớn là \(2a=4\Rightarrow a=2\) và hai tiêu điểm \({{F}_{1}}\left( 1;-1 \right);\,\,{{F}_{2}}\left( -1;1 \right)\Rightarrow c=\sqrt{2}\Rightarrow b=\sqrt{{{a}^{2}}-{{c}^{2}}}=\sqrt{2}\).

\(\begin{align}  \Rightarrow m=\max \left| z \right|=2;\,\,n=\min \left| z \right|=\sqrt{2} \\  \Rightarrow w=2+\sqrt{2}i\Rightarrow \left| w \right|=\sqrt{6}\Rightarrow {{\left| w \right|}^{2018}}={{6}^{1009}} \\ \end{align}\)

Chọn C.

Phương pháp giải:

Thay \(z = x + yi\), nhân liên hợp, xác định phần thực và phần ảo của số phức \(\frac{{z + i}}{{z - i}}\).

\(\frac{{z + i}}{{z - i}}\) là một số thực âm khi và chỉ khi \(\left\{ \begin{array}{l}{\mathop{\rm Re}\nolimits} \left( {\frac{{z + i}}{{z - i}}} \right) < 0\\{\mathop{\rm Im}\nolimits} \left( {\frac{{z + i}}{{z - i}}} \right) = 0\end{array} \right.\).

Lời giải chi tiết:

\(\begin{array}{l}\,\,\,\dfrac{{z + i}}{{z - i}} = \dfrac{{x + yi + i}}{{x + yi - i}} = \dfrac{{x + \left( {y + 1} \right)i}}{{x + \left( {y - 1} \right)i}}\\ = \dfrac{{\left[ {x + \left( {y + 1} \right)i} \right]\left[ {x - \left( {y - 1} \right)i} \right]}}{{\left[ {x + \left( {y - 1} \right)i} \right]\left[ {x - \left( {y - 1} \right)i} \right]}}\\ = \dfrac{{{x^2} - x\left( {y - 1} \right)i + x\left( {y + 1} \right)i + \left( {y + 1} \right)\left( {y - 1} \right)}}{{{x^2} + {{\left( {y - 1} \right)}^2}}}\\ = \dfrac{{{x^2} + {y^2} - 1 + \left( { - xy + x + xy + x} \right)i}}{{{x^2} + {{\left( {y - 1} \right)}^2}}}\\ = \dfrac{{{x^2} + {y^2} - 1}}{{{x^2} + {{\left( {y - 1} \right)}^2}}} + \dfrac{{2xi}}{{{x^2} + {{\left( {y - 1} \right)}^2}}}\end{array}\)

Để \(\dfrac{{z + i}}{{z - i}}\) là một số thực âm \( \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} - 1 < 0\\2x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\{y^2} < 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 0\\ - 1 < y < 1\end{array} \right.\)

Do đó tập hợp các điểm biểu diễn của z sao cho \(\dfrac{{z + i}}{{z - i}}\) là một số thực âm là các điểm trên trục tung với \( - 1 < y < 1\)

Chọn A.

Phương pháp giải:

Gọi \(z = a + bi\,\,\left( {a;b \in R} \right)\), tìm điều kiện để \(\frac{z}{{z - 6}}\) là số thuần ảo.

Suy ra các đường biểu diễn z thỏa mãn yêu cầu bài toán, tìm điều kiện để các đường biểu diễn đó có 1 điểm chung duy nhất.

Lời giải chi tiết:

Giả sử \(z = a + bi\left( {a,b \in R} \right),z \ne 6.\) M(a; b) là điểm biểu diễn z. Khi đó ta có

\(\frac{z}{{z - 6}} = \frac{{a + bi}}{{\left( {a + bi} \right) - 6}} = \frac{{\left( {a + bi} \right)\left( {a - 6 - bi} \right)}}{{\left( {a - 6 + bi} \right)\left( {a - 6 - bi} \right)}} = \frac{{a\left( {a - 6} \right) + {b^2} + i\left( {b\left( {a - 6} \right) - ab} \right)}}{{{{\left( {a - 6} \right)}^2} + {b^2}}}\)

Để \(\frac{z}{{z - 6}}\)  là số thuần ảo thì ta phải có \(a\left( {a - 6} \right) + {b^2} = 0 \Leftrightarrow {a^2} - 6a + {b^2} = 0\,\,\,\,\left( 1 \right)\)

Và \({\left( {a - 6} \right)^2} + {b^2} \ne 0\). Suy ra điểm M thuộc đường tròn tâm \(I\left( {3;0} \right)\) bán kính \(R = 3\).

Từ \(\left| {z - m} \right| = 4 \Leftrightarrow \left| {\left( {a + bi} \right) - m} \right| = 4 \Leftrightarrow {\left( {a - m} \right)^2} + {b^2} = 16\,\,\left( 2 \right)\)

Suy ra M thuộc đường tròn tâm \(I'\left( {m;0} \right);\) bán kính \(R' = 4\).

Để có đúng 1 điểm M thỏa mãn thì hai đường tròn \(\left( {I;R} \right);\,\,\left( {I';R'} \right)\) có 1 điểm chung duy nhất \( \Leftrightarrow \left[ \begin{array}{l}II' = R + R'\\II' = \left| {R - R'} \right|\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left| {m - 3} \right| = 7\\\left| {m - 3} \right| = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 10\\m =  - 4\\m = 4\\m = 2\end{array} \right.\)

Với \(m = 2;m = 10\) loại do hai đường tròn tiếp xúc tại điểm \(\left( {6;0} \right)\).

Vậy \(S = \left\{ { - 4;4} \right\}\)

Tổng các phần tử của S là \(4 - 4 = 0\)

Chọn A.

Phương pháp giải:

Áp dụng công thức : \(z.\overline{z}=|z{{|}^{2}}\)

Lời giải chi tiết:

 áp dụng công thức trên ta có :

\({{z}^{3}}+\frac{1}{{{z}^{3}}}={{z}^{3}}+\frac{{{\left( \overline{z} \right)}^{3}}}{{{\left( {{\left( |z| \right)}^{2}} \right)}^{3}}}={{z}^{3}}+{{\left( \overline{z} \right)}^{3}}\)

Đặt z = a + bi , ta có 

\(\begin{align}  & \text{w}={{\left( a+bi \right)}^{3}}+{{\left( a-bi \right)}^{3}} \\ & ={{a}^{3}}+3a{{\left( bi \right)}^{2}}+3{{a}^{2}}bi+{{\left( bi \right)}^{3}}+{{a}^{3}}+3a{{\left( -bi \right)}^{2}}+3{{a}^{2}}\left( -bi \right)+{{\left( -bi \right)}^{3}} \\ & =2{{a}^{3}}-6a{{b}^{2}} \\\end{align}\)

Mà có : \(|z|=1=>\sqrt{{{a}^{2}}+{{b}^{2}}}=1=>{{b}^{2}}=1-{{a}^{2}}\)

Suy ra :\(\text{w}=8{{a}^{3}}-6a\) với  a thuộc [ -1 ; 1 ]

Xét hàm \(f\left( a \right)=8{{a}^{3}}-6a\) trên đoạn [ -1 ; 1 ] ta được max = 2 ; min = - 2

Chọn đáp án A

Phương pháp giải:

Sử dụng phương pháp hình học để tính giá trị của P.

Chú ý: \(\left| {\dfrac{{{z_1}}}{{{z_2}}}} \right| = \dfrac{{\left| {{z_1}} \right|}}{{\left| {{z_2}} \right|}}\), \({a^2} = {b^2} + {c^2} - 2bc\cos A\)

Lời giải chi tiết:

Ta có: \(P = \left| {\dfrac{{{z_1} + {z_2}}}{{{z_1} - {z_2}}}} \right| = \dfrac{{\left| {{z_1} + {z_2}} \right|}}{{\left| {{z_1} - {z_2}} \right|}} = \dfrac{{OE}}{{OF}}\) (quan sát hình vẽ)

\(\begin{array}{l}O{E^2} = O{M^2} + M{E^2} - 2OM.ME.\cos {135^0} = 2 + 4 - 2\sqrt 2 .2.\left( { - \dfrac{{\sqrt 2 }}{2}} \right) = 10\\ \Rightarrow OE = \sqrt {10} \end{array}\)

\(\begin{array}{l}O{F^2} = O{M^2} + M{F^2} - 2OM.MF.\cos {45^0} = 2 + 4 - 2\sqrt 2 .2.\dfrac{{\sqrt 2 }}{2} = 2\\ \Rightarrow OF = \sqrt 2 \end{array}\)

\( \Rightarrow P = \dfrac{{OE}}{{OF}} = \sqrt 5 \).

Chọn: A

Phương pháp giải:

Lời giải chi tiết:

Giả sử \(z = a + bi,\left( {a,b \in \mathbb{R},b > 0} \right)\).

Ta có: \(\left| {z - 1} \right| = 5 \Leftrightarrow {\left( {a - 1} \right)^2} + {b^2} = 25 \Leftrightarrow {a^2} + {b^2} - 2a - 24 = 0\) (1)

\(\dfrac{1}{z} + \dfrac{1}{{\overline z }} = \dfrac{5}{{17}} \Leftrightarrow \dfrac{1}{{a + bi}} + \dfrac{1}{{a - bi}} = \dfrac{5}{{17}} \Leftrightarrow \dfrac{{2a}}{{{a^2} + {b^2}}} = \dfrac{5}{{17}} \Leftrightarrow {a^2} + {b^2} - \dfrac{{34}}{5}a = 0\) (2)

Từ (1) và (2) suy ra: \(a = 5\)\( \Rightarrow 25 + {b^2} - 34 = 0 \Leftrightarrow {b^2} = 9 \Leftrightarrow \left[ \begin{array}{l}b =  - 3\,(L)\\b = 3\end{array} \right.\) \( \Rightarrow z = 5 + 3i\)

Tổng phần thực vào phần ảo của \(z\) là: 8.

Chọn: D

Phương pháp giải:

+) Đặt \(\frac{1}{{\left| z \right| - z}} = 4 + bi\).

+) Thay vào biểu thức ban đầu, sử dụng phương pháp môđun hai vế.

Lời giải chi tiết:

Do \(\frac{1}{{\left| z \right| - z}}\) có phần thực bằng 4 nên giả sử: \(\frac{1}{{\left| z \right| - z}} = 4 + bi\)

\(\begin{array}{l} \Leftrightarrow 4\left| z \right| - 4z + b\left| z \right|i - bzi = 1 \Leftrightarrow \left( {4 + bi} \right)z = 4\left| z \right| - 1 + b\left| z \right|i\\ \Rightarrow \left| {\left( {4 + bi} \right)z} \right| = \left| {4\left| z \right| - 1 + b\left| z \right|i} \right| \Leftrightarrow \left| {4 + bi} \right|\left| z \right| = \left| {4\left| z \right| - 1 + b\left| z \right|i} \right|\\ \Leftrightarrow \sqrt {16 + {b^2}} .\left| z \right| = \sqrt {{{\left( {4\left| z \right| - 1} \right)}^2} + {b^2}{{\left| z \right|}^2}}  \Leftrightarrow \left( {16 + {b^2}} \right){\left| z \right|^2} = {\left( {4\left| z \right| - 1} \right)^2} + {b^2}{\left| z \right|^2}\\ \Leftrightarrow \left( {16 + {b^2}} \right){\left| z \right|^2} = 16{\left| z \right|^2} - 8\left| z \right| + 1 + {b^2}{\left| z \right|^2} \Leftrightarrow  - 8\left| z \right| + 1 = 0 \Leftrightarrow \left| z \right| = \frac{1}{8}\end{array}\)

Chọn: D

Phương pháp giải:

Giải phương trình đã cho để tìm \(z\) từ đó tính mô đun của \(w.\)

Số phức \(z = a + bi\,\,\left( {a;b \in \mathbb{R}} \right)\) có mô đun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \)

Lời giải chi tiết:

Ta có

\(\begin{array}{l}\left( {2 + i} \right)z + \dfrac{{2(1 + 2i)}}{{1 + i}} = 7 + 8i \Leftrightarrow \left( {2 + i} \right)z + \dfrac{{\left( {2 + 4i} \right)\left( {1 - i} \right)}}{{\left( {1 + i} \right)\left( {1 - i} \right)}} = 7 + 8i\\ \Leftrightarrow \left( {2 + i} \right)z + 3 + i = 7 + 8i \Leftrightarrow \left( {2 + i} \right)z = 4 + 7i\\ \Leftrightarrow z = \dfrac{{4 + 7i}}{{2 + i}} = \dfrac{{\left( {4 + 7i} \right)\left( {2 - i} \right)}}{{\left( {2 + i} \right)\left( {2 - i} \right)}} = 3 + 2i\end{array}\)

Suy ra \(w = z + 1 - 2i = 3 + 2i + 1 - 2i = 4 \Rightarrow \left| w \right| = 4.\)

Chọn D

Phương pháp giải:

Lời giải chi tiết:

Giả sử \({z_1} = a + bi\left( {a,b \in \mathbb{R},{a^2} + {b^2} > 0} \right) \Rightarrow {z_2} = a - bi\)

\(\begin{array}{l} + )\,\,{z_1} - {z_2} = 2bi \Rightarrow \left| {{z_1} - {z_2}} \right| = \left| {2bi} \right| = \left| {2b} \right| = 2\sqrt 3  \Leftrightarrow {b^2} = 3\\ + )\,\,\dfrac{{{z_1}}}{{z_2^2}} = \dfrac{{a + bi}}{{{{\left( {a - bi} \right)}^2}}} = \dfrac{{{{\left( {a + bi} \right)}^3}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}} = \dfrac{{{a^3} - 3a{b^2}}}{{{{\left( {{a^2} + {b^2}} \right)}^2}}} + \dfrac{{3{a^2}b - {b^3}}}{{{a^2} + {b^2}}}i\,\, \in \mathbb{R}\\ \Rightarrow \dfrac{{3{a^2}b - {b^3}}}{{{a^2} + {b^2}}} = 0 \Leftrightarrow b\left( {3{a^2} - {b^2}} \right) \Leftrightarrow \left[ \begin{array}{l}b = 0\\{b^2} = 3{a^2}\end{array} \right.\end{array}\)

+) \(b = 0 \Rightarrow {z_1} = \,\,{z_2} = a \Rightarrow \)\(\left| {{z_1} - {z_2}} \right| = 0 \ne 2\sqrt 3  \Rightarrow \) Loại

+) \({b^2} = 3{a^2} \Leftrightarrow {a^2} = 1 \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}}  = \sqrt {1 + 3}  = 2\)

Chọn: C

Phương pháp giải:

Thu gọn số phức \(z\) rồi suy ra \({z^4}\).

Lời giải chi tiết:

Ta có : \(\frac{{1 + i}}{{1 - i}} = \frac{{\left( {1 + i} \right)\left( {1 + i} \right)}}{{1 + 1}} = \frac{{2i}}{2} = i\) \( \Rightarrow z = {\left( {\frac{{1 + i}}{{1 - i}}} \right)^{2019}} = {i^{2019}}\)

\( \Rightarrow {z^4} = {\left( {{i^{2019}}} \right)^4} = {\left( {{i^4}} \right)^{2019}} = 1\).

Chọn D.

Phương pháp giải:

- Viết \({z_1} = ki{z_2}\left( {k \in \mathbb{R}} \right)\), thay vào đẳng thúc bài cho tìm \(\left| {{z_2}} \right|,\left| {{z_1}} \right|\) theo \(k\).

- Tìm GTLN của \(\left| {{z_1}} \right| + \left| {{z_2}} \right|\) và kết luận.

Lời giải chi tiết:

Ta có : \(\dfrac{{{z_1}}}{{{z_2}}}\) là số thuần ảo nên ta viết lại \(\dfrac{{{z_1}}}{{{z_2}}} = ki \Leftrightarrow {z_1} = ki{z_2}\)

Khi đó \(\left| {{z_1} - {z_2}} \right| = 10 \Leftrightarrow \left| {ki{z_2} - {z_2}} \right| = 10 \Leftrightarrow \left| {{z_2}\left( { - 1 + ki} \right)} \right| = 10\) \( \Leftrightarrow \left| {{z_2}} \right| = \dfrac{{10}}{{\left| { - 1 + ki} \right|}} = \dfrac{{10}}{{\sqrt {{k^2} + 1} }}\)

\( \Rightarrow \left| {{z_1}} \right| = \left| {ki} \right|.\left| {{z_2}} \right| = \left| k \right|.\dfrac{{10}}{{{k^2} + 1}}\) \( \Rightarrow \left| {{z_1}} \right| + \left| {{z_2}} \right| = \dfrac{{10\left| k \right|}}{{\sqrt {{k^2} + 1} }} + \dfrac{{10}}{{\sqrt {{k^2} + 1} }} = \dfrac{{10\left( {\left| k \right| + 1} \right)}}{{\sqrt {{k^2} + 1} }}\)

Xét \(y = f\left( t \right) = \dfrac{{10\left( {t + 1} \right)}}{{\sqrt {{t^2} + 1} }}\) \( \Rightarrow 10\left( {t + 1} \right) = y\sqrt {{t^2} + 1}  \Leftrightarrow 100{\left( {t + 1} \right)^2} = {y^2}\left( {{t^2} + 1} \right)\)

\( \Leftrightarrow 100\left( {{t^2} + 2t + 1} \right) = {y^2}{t^2} + {y^2} \Leftrightarrow \left( {{y^2} - 100} \right){t^2} - 200t + {y^2} - 100 = 0\)

Phương trình có nghiệm \( \Leftrightarrow \Delta ' = {100^2} - {\left( {{y^2} - 100} \right)^2} = {y^2}\left( {200 - {y^2}} \right) \ge 0\) \( \Leftrightarrow  - 10\sqrt 2  \le y \le 10\sqrt 2 \)

Vậy \(\max y = 10\sqrt 2 \) khi \(t = 1\) hay \(k =  \pm 1\).

Chọn B.

Phương pháp giải:

Cô lập \(z\), sử dụng phương pháp môđun hai vế.

Lời giải chi tiết:

Theo bài ra ta có:

\(\begin{array}{l}\left( {z + \dfrac{5}{{\left| z \right|}}} \right)i = 7 - z \Leftrightarrow zi + \dfrac{{5i}}{{\left| z \right|}} = 7 - z \Leftrightarrow z\left( {i + 1} \right) = 7 - \dfrac{{5i}}{{\left| z \right|}}\\ \Leftrightarrow 2{\left| z \right|^2} = 49 + \dfrac{{25}}{{{{\left| z \right|}^2}}} \Leftrightarrow 2{\left| z \right|^4} - 49{\left| z \right|^2} - 25 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{\left| z \right|^2} = 25\,\,\left( {tm} \right)\\\left| z \right| =  - \dfrac{1}{2}\,\,\left( {ktm} \right)\end{array} \right. \Leftrightarrow \left| z \right| = 5\,\,\left( {Do\,\,\left| z \right| > 0} \right)\end{array}\)

Thay \(\left| z \right| = 5\) vào biểu thức đề bài ta có:

\(\left( {z + 1} \right)i = 7 - z \Leftrightarrow z\left( {i + 1} \right) = 7 - i \Leftrightarrow z = \dfrac{{7 - i}}{{i + 1}} = 3 - 4i\).

Chọn C.

Phương pháp giải:

Gọi \(z = \sqrt 2  + yi\,\,\left( {y \in \mathbb{R}} \right)\). Sử dụng phương pháp hàm số.

Lời giải chi tiết:

Gọi \(z = \sqrt 2  + yi\,\,\left( {y \in \mathbb{R}} \right)\). Theo bài ra ta có:

\(\left| {\dfrac{1}{z} - i} \right| = \dfrac{{\left| {1 - iz} \right|}}{{\left| z \right|}} = \dfrac{{\left| {1 - i\left( {\sqrt 2  + yi} \right)} \right|}}{{\sqrt {2 + {y^2}} }} = \sqrt {\dfrac{{2 + {{\left( {1 + y} \right)}^2}}}{{2 + {y^2}}}}  = \sqrt {f\left( y \right)} \).

Xét hàm số

\(\begin{array}{l}f\left( y \right) = \dfrac{{2 + {{\left( {1 + y} \right)}^2}}}{{2 + {y^2}}} = \dfrac{{3 + 2y + {y^2}}}{{2 + {y^2}}} = 1 + \dfrac{{1 + 2y}}{{2 + {y^2}}}\\f'\left( y \right) = \dfrac{{2\left( {2 + {y^2}} \right) - \left( {1 + 2y} \right).2y}}{{{{\left( {2 + y} \right)}^2}}} = \dfrac{{4 + 2{y^2} - 2y - 4{y^2}}}{{{{\left( {2 + y} \right)}^2}}} = \dfrac{{ - 2{y^2} - 2y + 4}}{{{{\left( {2 + y} \right)}^2}}}\\f'\left( y \right) = 0 \Leftrightarrow  - 2{y^2} - 2y + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}y = 1\\y =  - 2\end{array} \right.\end{array}\)

BBT:

Từ BBT \( \Rightarrow \max f\left( y \right) = f\left( 1 \right) = 2 \Leftrightarrow \max \left| {\dfrac{1}{z} - i} \right| = \sqrt 2 \).

Chọn A.

Phương pháp giải:

- \(z = a + bi \Rightarrow \overline z  = a - bi\).

- Tìm \(\overline z \) từ giả thiết, sau đó suy ra \(z\).

Lời giải chi tiết:

Ta có

\(\begin{array}{l}\overline z \left( {1 + i} \right) = 3 - i\\ \Rightarrow \overline z  = \dfrac{{3 - i}}{{1 + i}} = 1 - 2i\\ \Rightarrow z = 1 + 2i\\ \Rightarrow a = 1,\,\,b = 2\\ \Rightarrow a - 2b = 1 - 2.2 =  - 3.\end{array}\)

Chọn B.

Phương pháp giải:

- Tính \(w = {z^2}\) rồi suy ra \(\left| {\rm{w}} \right|\).

- Giải phương trình tìm \(m\).

Lời giải chi tiết:

Ta có \(z = \dfrac{{m + 3i}}{{1 - i}}\).

\(\begin{array}{l} \Rightarrow w = {z^2} = {\left( {\dfrac{{m + 3i}}{{1 - i}}} \right)^2}\\ \Rightarrow w = \dfrac{{{m^2} + 6mi - 9}}{{ - 2i}} = \dfrac{{\left( {{m^2} - 9} \right) + 6mi}}{{ - 2i}}\\\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\left( {{m^2} - 9} \right)i + 6m{i^2}}}{{ - 2{i^2}}} = \dfrac{{\left( {{m^2} - 9} \right)i - 6m}}{2}\\ \Rightarrow \left| w \right| = \dfrac{{\sqrt {{{\left( {{m^2} - 9} \right)}^2} + 36{m^2}} }}{2}\end{array}\)

Theo bài ra ta có:

\(\begin{array}{l}\left| w \right| = 9 \Leftrightarrow \dfrac{{\sqrt {{{\left( {{m^2} - 9} \right)}^2} + 36{m^2}} }}{2} = 9\\ \Leftrightarrow \sqrt {{{\left( {{m^2} - 9} \right)}^2} + 36{m^2}}  = 18\\ \Leftrightarrow {\left( {{m^2} - 9} \right)^2} + 36{m^2} = 324\\ \Leftrightarrow {m^4} + 18{m^2} - 243 = 0\\ \Leftrightarrow \left[ \begin{array}{l}{m^2} = 9\\{m^2} =  - 27\,\,\,\left( {ktm} \right)\end{array} \right. \Leftrightarrow m =  \pm 3\end{array}\)

Vậy \(m =  \pm 3\).

Chọn C.

Phương pháp giải:

- Đặt \(z = a + bi \Rightarrow \overline z  = a - bi\).

- Thay vào biểu thức, nhân chéo sau đó tìm \(a,\,\,b\).

- Suy ra số phức \(z\) và tính \({\rm{w}} = 1 + z + {z^2}\).

Lời giải chi tiết:

Đặt \(z = a + bi \Rightarrow \overline z  = a - bi\).

Theo bài ra ta có:

\(\begin{array}{l}\,\,\,\,\,\dfrac{{5\left( {\overline z  + i} \right)}}{{z + 1}} = 2 - i\\ \Rightarrow \dfrac{{5\left( {a - bi + i} \right)}}{{a + bi + 1}} = 2 - i\\ \Leftrightarrow 5\left[ {a - \left( {b - 1} \right)i} \right] = \left( {a + 1 + bi} \right)\left( {2 - i} \right)\\ \Leftrightarrow 5a - 5\left( {b - 1} \right)i = 2\left( {a + 1} \right) + b + \left( {2b - a - 1} \right)i\\ \Leftrightarrow \left\{ \begin{array}{l}5a = 2a + 2 + b\\5 - 5b = 2b - a - 1\end{array} \right. \Rightarrow a = b = 1\\ \Rightarrow z = 1 + i \Rightarrow {z^2} = 2i\\ \Rightarrow {\rm{w}} = 1 + z + {z^2} = 1 + 1 + i + 2i = 2 + 3i\end{array}\)

Vậy \(\left| {\rm{w}} \right| = \sqrt {{2^2} + {3^2}}  = \sqrt {13} .\)

Chọn C.

Phương pháp giải:

- Tìm số phức z bằng MTCT rồi suy ra \(\overline z \): Số phức \(z = a + bi\) có số phức liên hợp \(\overline z  = a - bi\).

- Xác định các hệ số \(a,\,\,b\) và tính tổng \(a + b\).

Lời giải chi tiết:

Ta có \(\dfrac{{\left( { - 1 + i} \right)z + 2}}{{1 - 2i}} = 2 + 3i \Rightarrow z = \dfrac{{\left( {2 + 3i} \right)\left( {1 - 2i} \right) - 2}}{{ - 1 + i}} =  - \dfrac{7}{2} - \dfrac{5}{2}i\)

\(\begin{array}{l} \Rightarrow \overline z  =  - \dfrac{7}{2} + \dfrac{5}{2}i\\ \Rightarrow a =  - \dfrac{7}{2};\,\,b = \dfrac{5}{2}\end{array}\)

Vậy \(a + b =  - \dfrac{7}{2} + \dfrac{5}{2} =  - 1.\)

Chọn A.

Phương pháp giải:

- Áp dụng công thức \(z.\overline z  = {\left| z \right|^2}\).

- Quy đồng mẫu tìm số phức \(z\).

- Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \).

Lời giải chi tiết:

Ta có

\(\begin{array}{l}\dfrac{{3 - 4i}}{z} = \dfrac{{\left( {2 + 3i} \right)\overline z }}{{{{\left| z \right|}^2}}} + 2 + i\\ \Leftrightarrow \dfrac{{3 - 4i}}{z} = \dfrac{{\left( {2 + 3i} \right)\overline z }}{{z.\overline z }} + 2 + i\\ \Leftrightarrow \dfrac{{3 - 4i}}{z} = \dfrac{{2 + 3i}}{z} + 2 + i\\ \Leftrightarrow 3 - 4i = 2 + 3i + \left( {2 + i} \right).z\\ \Leftrightarrow \left( {2 + i} \right).z = 1 - 7i\\ \Leftrightarrow z = \dfrac{{1 - 7i}}{{2 + i}} =  - 1 - 3i\end{array}\)

Vậy \(\left| z \right| = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 3} \right)}^2}}  = \sqrt {10} .\)

Chọn B.

Phương pháp giải:

Cho số phức \(z = a + bi\,\,\,\left( {a,\,\,b \in \mathbb{R}} \right).\) Khi đó số phức liên hợp của \(z\) là \(\overline z  = a - bi.\)

Lời giải chi tiết:

Ta có: \(z = \dfrac{i}{{1 + i}} = \dfrac{{i\left( {1 - i} \right)}}{{\left( {1 + i} \right)\left( {1 - i} \right)}}\)\( = \dfrac{{i - {i^2}}}{2} = \dfrac{{1 + i}}{2}\)

\( \Rightarrow \) Số phức liên hợp với số phức đã cho là: \(\overline z  = \dfrac{{1 - i}}{2}.\)

Chọn D.

Phương pháp giải:

Modun của số phức \(z = x + yi:\;\;\left| z \right| = \sqrt {{x^2} + {y^2}} .\)

Rút gọn số phức \(z\) rồi tính modun của số phức.

Lời giải chi tiết:

Ta có: \(z = \dfrac{1}{{1 + i}} + \dfrac{2}{{1 - i}} = \dfrac{{1 - i}}{{1 - {i^2}}} + \dfrac{{2\left( {1 + i} \right)}}{{1 - {i^2}}}\)\( = \dfrac{{1 - i}}{2} + \dfrac{{2 + 2i}}{2} = \dfrac{{3 + i}}{2}\)

\( \Rightarrow \left| z \right| = \sqrt {{{\left( {\dfrac{3}{2}} \right)}^2} + {{\left( {\dfrac{1}{2}} \right)}^2}}  = \dfrac{{\sqrt {10} }}{2}.\)

Chọn B.

Phương pháp giải:

Gọi số phức cần tìm là \(z=a+bi\), thay vào các hệ thức trong bài và tìm \(a,b\Rightarrow z\).

Số phức \(z=a+bi\) là số thuần ảo nếu \(a=0\).

Lời giải chi tiết:

Giả sử \(z=a+bi\left( z\ne 4 \right)\) , ta có \(|z-3i|=5\Leftrightarrow |a+bi-3i|=5 \)

\( \Leftrightarrow {{a}^{2}}+{{(b-3)}^{2}}=25 \) \( \Leftrightarrow {{a}^{2}}+{{b}^{2}}-6b=16\)  (1)

Mặt khác \(\frac{z}{{z - 4}} = \frac{{a + bi}}{{a + bi - 4}} = \frac{{(a + bi)(a - 4 - bi)}}{{{{(a - 4)}^2} + {b^2}}} = \frac{{({a^2} - 4a + {b^2}) - 4bi}}{{{{(a - 4)}^2} + {b^2}}}\)

\(\frac{z}{z-4}\) là số thuần ảo khi \({{a}^{2}}-4a+{{b}^{2}}=0\)  (2)

Giải hệ (1) và (2):

Lấy  trừ  vế với vế ta được:

\(4a-6b=16\Leftrightarrow 2a-8=3b\Leftrightarrow 2\left( a-4 \right)=3b\Leftrightarrow a-4=\frac{3b}{2}\).

Thay \(a-4=\frac{3b}{2}\) vào  ta được:

\(a.\frac{{3b}}{2} + {b^2} = 0 \Leftrightarrow b\left( {\frac{{3a}}{2} + b} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}b = 0\\b =  - \frac{{3a}}{2}\end{array} \right.\).

Nếu \(b=0\) thì \(a=4\Rightarrow z=4\) (loại do \(z\ne 4\)

Nếu \(b=-\frac{3a}{2}\) thì \(a - 4 =  - \frac{{9a}}{4} \Leftrightarrow a = \frac{{16}}{{13}} \)

\( \Rightarrow b =  - \frac{{24}}{{13}} \Rightarrow z = \frac{{16}}{{13}} - \frac{{24}}{{13}}i\) (thỏa mãn)

Vậy có 1  số phức thỏa mãn bài toán.

Chọn D

Phương pháp giải:

- Tính số phức \(z\Rightarrow z.{{z}^{7}}.{{z}^{15}}\)(lưu ý: \({{i}^{4k}}=1;{{i}^{4k+1}}=i;{{i}^{4k+2}}=-1;{{i}^{4k+3}}=-i\)).

Lời giải chi tiết:

Ta có : \(\frac{1+i}{1-i}=\frac{(1+i)(1+i)}{(1i)(1+i)}=\frac{1+2i+{{i}^{2}}}{{{1}^{2}}+{{1}^{2}}}=\frac{2i}{2}=i\)

\(\Rightarrow z={{i}^{2017}}=i.{{i}^{2016}}=i.{{\left( {{i}^{4}} \right)}^{504}}=i{{.1}^{504}}=i\)

 \(\Rightarrow z.{{z}^{7}}.{{z}^{15}}=i.{{i}^{7}}.{{i}^{15}}={{i}^{23}}=i.{{i}^{22}}=i.{{\left( {{i}^{2}} \right)}^{11}}=i.{{\left( -1 \right)}^{11}}=-i\)

Chọn D

Phương pháp giải:

Chuyến vế, lấy môđun hai vế, đưa về phương trình trùng phương.

Lời giải chi tiết:

\(\begin{align}  & \,\,\,\,\,\left( 3+i \right)\left| z \right|=\frac{-2+14i}{z}+1-3i \\  & \Leftrightarrow \left( 3+i \right)\left| z \right|-1+3i=\frac{-2+14i}{z} \\  & \Leftrightarrow \left( 3\left| z \right|-1 \right)+\left( \left| z \right|+3 \right)i=\frac{-2+14i}{z} \\ \end{align}\)

Lấy mođun hai vế ta có : \(\sqrt{9{{\left| z \right|}^{2}}-6\left| z \right|+1+{{\left| z \right|}^{2}}+6\left| z \right|+9}=\frac{10\sqrt{2}}{\left| z \right|}\)

\( \Leftrightarrow 10{\left| z \right|^2} + 10 = \frac{{200}}{{{{\left| z \right|}^2}}} \Leftrightarrow {\left| z \right|^4} + {\left| z \right|^2} - 20 = 0 \Leftrightarrow {\left| z \right|^2} = 4 \Rightarrow \left| z \right| = 2 \in \left( {\frac{7}{4};\frac{{11}}{5}} \right)\)

Chọn D. 

Phương pháp giải:

Sử dụng BĐT \(\left| {{z_1} + {z_3}} \right| \le \left| {{z_1}} \right| + \left| {{z_2}} \right|\).

Lời giải chi tiết:

Dễ dàng kiểm tra \(z = 0\) không thỏa mãn \(\left( {3 - i} \right)\left| z \right| = \frac{z}{{w - 1}} + 1 - i\)

Ta có: \(\left( {3 - i} \right)\left| z \right| = \frac{z}{{w - 1}} + 1 - i \Leftrightarrow \frac{z}{{w - 1}} = \left( {3 - i} \right)\left| z \right| + i - 1 \Leftrightarrow \frac{z}{{w - 1}} = \left( {3\left| z \right| - 1} \right) + \left( {1 - \left| z \right|} \right)i\)\( \Rightarrow \left| {\frac{z}{{w - 1}}} \right| = \sqrt {10{{\left| z \right|}^2} - 8\left| z \right| + 2} \)\( \Rightarrow \left| {w - 1} \right| = \sqrt {\frac{{{{\left| z \right|}^2}}}{{10{{\left| z \right|}^2} - 8\left| z \right| + 2}}} \)

Nhận xét: \(T = \left| {w + i} \right| \le \left| {w - 1} \right| + \left| {1 + i} \right| = \frac{1}{{\sqrt {\frac{2}{{{{\left| z \right|}^2}}} - \frac{8}{{\left| z \right|}} + 10} }} + \sqrt 2  = \frac{1}{{\sqrt {2{{\left( {\frac{1}{{\left| z \right|}} - 2} \right)}^2} + 2} }} + \sqrt 2  \le \frac{{3\sqrt 2 }}{2}\)

Dấu “=” xảy ra khi và chỉ khỉ \(\left\{ \begin{array}{l}\left| z \right| = \frac{1}{2}\\w - 1 = k\left( {1 + i} \right)\\\left( {3 - i} \right)\left| z \right| = \frac{z}{{w - 1}} + 1 - i\end{array} \right.,\left( {k > 0} \right) \Leftrightarrow \left\{ \begin{array}{l}z = \frac{1}{2}i\\w = \frac{3}{2} + \frac{1}{2}i\end{array} \right.\)

Vậy, \(\max T = \frac{{3\sqrt 2 }}{2}\).

Chọn: B

Phương pháp giải:

Lời giải chi tiết:

\(\begin{array}{l}\frac{{\left( {\left| z \right| - 1} \right)\left( {1 + iz} \right)}}{{z - \frac{1}{{\bar z}}}} = i \Leftrightarrow \frac{{\left( {\left| z \right| - 1} \right)\left( {1 + iz} \right)\overline z }}{{{{\left| z \right|}^2} - 1}} = i\,\,\left( {\left| z \right| \ne 1} \right)\\ \Leftrightarrow \left( {\left| z \right| - 1} \right)\left( {1 + iz} \right)\overline z  = i\left( {\left| z \right| - 1} \right)\left( {\left| z \right| + 1} \right)\\ \Leftrightarrow \left( {\left| z \right| - 1} \right)\left[ {\left( {1 + iz} \right)\overline z  - i\left( {\left| z \right| + 1} \right)} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}\left| z \right| = 1\,\,\left( {ktm} \right)\\\overline z  + i{\left| z \right|^2} - i\left| z \right| - i = 0\end{array} \right. \Leftrightarrow \overline z  + i\left( {{{\left| z \right|}^2} - \left| z \right| - 1} \right) = 0\\ \Leftrightarrow \overline z  =  - i\left( {{{\left| z \right|}^2} - \left| z \right| - 1} \right) \Leftrightarrow \left| {\overline z } \right| = \left| {{{\left| z \right|}^2} - \left| z \right| - 1} \right|\\ \Leftrightarrow {\left| z \right|^2} = {\left| z \right|^4} + {\left| z \right|^2} + 1 - 2{\left| z \right|^3} - 2{\left| z \right|^2} + 2\left| z \right|\\ \Leftrightarrow {\left| z \right|^4} - 2{\left| z \right|^3} - 2{\left| z \right|^2} + 2\left| z \right| + 1 = 0\\ \Leftrightarrow \left( {\left| z \right| - 1} \right)\left( {\left| z \right| + 1} \right)\left( {{{\left| z \right|}^2} - 2\left| z \right| - 1} \right) = 0\\ \Leftrightarrow {\left| z \right|^2} - 2\left| z \right| - 1 = 0 \Leftrightarrow \left| z \right| = 1 + \sqrt 2 \\ \Rightarrow {a^2} + {b^2} = {\left| z \right|^2} = 3 + 2\sqrt 2 \end{array}\)

Chọn C.