40 bài tập vận dụng Biến đổi đơn giản biểu thức chứa căn thức bậc haiLàm bàiCâu hỏi 1 : Thu gọn biểu thức: \(A=\frac{\left( 5+2\sqrt{6} \right)\left( 49-20\sqrt{6} \right)\sqrt{5-2\sqrt{6}}}{9\sqrt{3}-11\sqrt{2}}\) Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l}A = \frac{{\left( {5 + 2\sqrt 6 } \right)\left( {49 - 20\sqrt 6 } \right)\sqrt {5 - 2\sqrt 6 } }}{{9\sqrt 3 - 11\sqrt 2 }}\\ = \frac{{\sqrt {5 + 2\sqrt 6 } .\sqrt {5 + 2\sqrt 6 } .\sqrt {5 - 2\sqrt 6 } \left( {49 - 20\sqrt 6 } \right)}}{{9\sqrt 3 - 11\sqrt 2 }}\\ = \frac{{\sqrt {{{\sqrt 3 }^2} + 2\sqrt 3 .\sqrt 2 + {{\sqrt 2 }^2}} .\sqrt {\left( {5 + 2\sqrt 6 } \right)\left( {5 - 2\sqrt 6 } \right)} \left( {49 - 20\sqrt 6 } \right)}}{{9\sqrt 3 - 11\sqrt 2 }}\\ = \frac{{\sqrt {{{\left( {\sqrt 3 + \sqrt 2 } \right)}^2}} .1.\left( {49 - 20\sqrt 6 } \right)}}{{9\sqrt 3 - 11\sqrt 2 }}\\ = \frac{{\left( {\sqrt 3 + \sqrt 2 } \right).\left( {49 - 20\sqrt 6 } \right)}}{{9\sqrt 3 - 11\sqrt 2 }}\\ = \frac{{49\sqrt 3 - 60\sqrt 2 + 49\sqrt 2 - 40\sqrt 3 }}{{9\sqrt 3 - 11\sqrt 2 }}\\ = \frac{{9\sqrt 3 - 11\sqrt 2 }}{{9\sqrt 3 - 11\sqrt 2 }}\\ = 1\end{array}\) Câu hỏi 2 : Tính: \(A=\frac{\sqrt{2}}{2\sqrt{2}+\sqrt{3+\sqrt{5}}}+\frac{\sqrt{2}}{2\sqrt{2}-\sqrt{3-\sqrt{5}}}\)
Đáp án: A Phương pháp giải: Lời giải chi tiết: Ta có \(\begin{array}{l}A = \frac{{\sqrt 2 }}{{2\sqrt 2 + \sqrt {3 + \sqrt 5 } }} + \frac{{\sqrt 2 }}{{2\sqrt 2 - \sqrt {3 - \sqrt 5 } }}\\= \frac{{\sqrt 2 .\sqrt 2 }}{{2\sqrt 2 .\sqrt 2 + \sqrt 2 .\sqrt {3 + \sqrt 5 } }} + \frac{{\sqrt 2 .\sqrt 2 }}{{2\sqrt 2 .\sqrt 2 - \sqrt 2 .\sqrt {3 - \sqrt 5 } }}\\= \frac{2}{{4 + \sqrt {6 + 2\sqrt 5 } }} + \frac{2}{{4 - \sqrt {6 - 2\sqrt 5 } }}\\= \frac{2}{{4 + \sqrt {{{\sqrt 5 }^2} + 2\sqrt 5 + 1} }} + \frac{2}{{4 - \sqrt {{{\sqrt 5 }^2} - 2\sqrt 5 + 1} }}\\= \frac{2}{{4 + \sqrt {{{\left( {\sqrt 5 + 1} \right)}^2}} }} + \frac{2}{{4 - \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} }}\\= \frac{2}{{4 + \sqrt 5 + 1}} + \frac{2}{{4 - \sqrt 5 + 1}}\\= \frac{2}{{5 + \sqrt 5 }} + \frac{2}{{5 - \sqrt 5 }}\\= \frac{{2.\left( {5 - \sqrt 5 } \right) + 2.\left( {5 + \sqrt 5 } \right)}}{{\left( {5 + \sqrt 5 } \right).\left( {5 - \sqrt 5 } \right)}}\\= \frac{{10 - 2\sqrt 5 + 10 + 2\sqrt 5 }}{{20}} = 1\end{array}\) Câu hỏi 3 : Thực hiện phép tính: 1)\(A = \sqrt {12} - 2\sqrt {48} + \frac{7}{5}\sqrt {75} \) 2)\(B = \sqrt {14 - 6\sqrt 5 } + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \)
Đáp án: A Phương pháp giải: 1) Áp dụng công thức \(\sqrt {{a^2}b} = a\sqrt b \left( {a,b \ge 0} \right)\) 2) Áp dụng công thức \(\sqrt {{a^2}} = \left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;a\; < \;0\end{array} \right..\) Lời giải chi tiết: Thực hiện phép tính: \(\begin{array}{l}1)\;\;A = \sqrt {12} - 2\sqrt {48} + \frac{7}{5}\sqrt {75} \\\;\;\; = \sqrt {{2^2}.3} - 2\sqrt {{4^2}.3} + \frac{7}{5}\sqrt {{5^2}.3} \\\;\;\; = 2\sqrt 3 - 2.4\sqrt 3 + \frac{7}{5}.5\sqrt 3 = \sqrt 3 .\end{array}\) Vậy \(A = \sqrt 3 \).\(\) \(\begin{array}{l}2)\;\;B = \sqrt {14 - 6\sqrt 5 } + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \sqrt {{3^2} + 2.3.\sqrt 5 + {{\left( {\sqrt 5 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \sqrt {{{\left( {3 + \sqrt 5 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \left| {3 + \sqrt 5 } \right| + \left| {2 - \sqrt 5 } \right|\\\;\;\;\;\;\;\; = 3 + \sqrt 5 + \sqrt 5 - 2\; = 2\sqrt {5 + 1} .\;\;\;\left( {do\;\;\;\sqrt 5 - 2 > 0} \right)\end{array}\) Vậy \(B = 2\sqrt 5 + 1\) Chọn A. Câu hỏi 4 : Hãy tính giá trị của: a) \(M = \left( {2\sqrt {300} + 3\sqrt {48} - 4\sqrt {75} } \right):\sqrt 3 \) ; b) \(N = \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} + \sqrt {4 - 2\sqrt 3 } \) ; c) \(P = \frac{2}{{\sqrt 3 + 1}} - \frac{1}{{\sqrt 3 - 2}} + \frac{{12}}{{\sqrt 3 + 3}}\).
Đáp án: A Phương pháp giải: +) Rút gọn căn bậc hai +) Sử dụng công thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,\,A \ge 0\\ - A\,\,khi\,\,A < 0\end{array} \right.\) +) Sử dụng hằng đẳng thức, trục căn thức ở mẫu Lời giải chi tiết: a) \(M = \left( {2\sqrt {300} + 3\sqrt {48} - 4\sqrt {75} } \right):\sqrt 3 \) \(\begin{array}{l}M = \left( {2\sqrt {300} + 3\sqrt {48} - 4\sqrt {75} } \right):\sqrt 3 = \left( {2.10\sqrt 3 + 3.4\sqrt 3 - 4.5\sqrt 3 } \right):\sqrt 3 \\\,\,\,\,\,\,\, = \left( {20\sqrt 3 + 12\sqrt 3 - 20\sqrt 3 } \right):\sqrt 3 = 12\sqrt 3 :\sqrt 3 = 12\end{array}\) b) \(N = \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} + \sqrt {4 - 2\sqrt 3 } \) ; \(\begin{array}{l}N = \sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} + \sqrt {4 - 2\sqrt 3 } = \left| {\sqrt 3 - 2} \right| + \sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} = 2 - \sqrt 3 + \left| {\sqrt 3 - 1} \right|\\\,\,\,\,\,\, = 2 - \sqrt 3 + \sqrt 3 - 1 = 1\end{array}\) c) \(P = \frac{2}{{\sqrt 3 + 1}} - \frac{1}{{\sqrt 3 - 2}} + \frac{{12}}{{\sqrt 3 + 3}}\) ; \(\begin{array}{l}P = \frac{2}{{\sqrt 3 + 1}} - \frac{1}{{\sqrt 3 - 2}} + \frac{{12}}{{\sqrt 3 + 3}} = \frac{{2\left( {\sqrt 3 - 1} \right)}}{{\left( {\sqrt 3 + 1} \right)\left( {\sqrt 3 - 1} \right)}} - \frac{{1\left( {\sqrt 3 + 2} \right)}}{{\left( {\sqrt 3 - 2} \right)\left( {\sqrt 3 + 2} \right)}} + \frac{{12\left( {3 - \sqrt 3 } \right)}}{{\left( {3 + \sqrt 3 } \right)\left( {3 - \sqrt 3 } \right)}}\\\,\,\,\,\, = \frac{{2\left( {\sqrt 3 - 1} \right)}}{2} - \frac{{\sqrt 3 + 2}}{{ - 1}} + \frac{{12\left( {3 - \sqrt 3 } \right)}}{6} = \sqrt 3 - 1 + \sqrt 3 + 2 + 2\left( {3 - \sqrt 3 } \right) = 7\end{array}\) Chọn A. Câu hỏi 5 : Thực hiện phép tính a) \(2\sqrt {50} - 3\sqrt {32} - \sqrt {162} + 5\sqrt {98} \) b) \(\sqrt {8 + 2\sqrt 7 } + \sqrt {11 - 4\sqrt 7 } \) c) \(\frac{{10}}{{\sqrt 5 }} + \frac{8}{{3 + \sqrt 5 }} - \frac{{\sqrt {18} - 3\sqrt 5 }}{{\sqrt 2 - \sqrt 5 }}\)
Đáp án: A Phương pháp giải: a) Rút gọn căn thức b) Sử dụng công thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\;\;khi\;\;A \ge 0\\ - A\;\;khi\;\;A < 0\end{array} \right..\) c) Trục căn thức ở mẫu, rút gọn. Lời giải chi tiết: a) \(2\sqrt {50} - 3\sqrt {32} - \sqrt {162} + 5\sqrt {98} = 10\sqrt 2 - 12\sqrt 2 - 9\sqrt 2 + 35\sqrt 2 = 24\sqrt 2 .\) \(\begin{array}{l}b)\;\sqrt {8 + 2\sqrt 7 } + \sqrt {11 - 4\sqrt 7 } = \sqrt {{{\left( {\sqrt 7 + 1} \right)}^2}} + \sqrt {{{\left( {\sqrt 7 - 2} \right)}^2}} = \left| {\sqrt 7 + 1} \right| + \left| {\sqrt 7 - 2} \right|\\ = \sqrt 7 + 1 + \sqrt 7 - 2 = 2\sqrt 7 - 1.\end{array}\) \(\begin{array}{l}c)\;\frac{{10}}{{\sqrt 5 }} + \frac{8}{{3 + \sqrt 5 }} - \frac{{\sqrt {18} - 3\sqrt 5 }}{{\sqrt 2 - \sqrt 5 }} = 2\sqrt 5 + \frac{{8\left( {3 - \sqrt 5 } \right)}}{{9 - 5}} - \frac{{3\left( {\sqrt 2 - \sqrt 5 } \right)}}{{\sqrt 2 - \sqrt 5 }}\\ = 2\sqrt 5 + 2\left( {3 - \sqrt 5 } \right) - 3 = 2\sqrt 5 + 6 - 2\sqrt 5 - 3 = 3\end{array}\) Chọn A. Câu hỏi 6 : Thực hiện phép tính: a) \(3\sqrt {\frac{1}{3}} + 4\sqrt {12} - 5\sqrt {27} \) b) \(\frac{{3 + 2\sqrt 3 }}{{\sqrt 3 }} - \frac{2}{{\sqrt 3 - 1}}\)
Đáp án: A Phương pháp giải: a) Rút gọn căn bậc hai b) Trục căn thức ở mẫu Lời giải chi tiết: Thực hiện phép tính: a) \(3\sqrt {\frac{1}{3}} + 4\sqrt {12} - 5\sqrt {27} = \sqrt 3 + 8\sqrt 3 - 15\sqrt 3 = - 6\sqrt 3 \) b) \(\frac{{3 + 2\sqrt 3 }}{{\sqrt 3 }} - \frac{2}{{\sqrt 3 - 1}} = \frac{{\left( {\sqrt 3 + 2} \right)\sqrt 3 }}{{\sqrt 3 }} - \frac{{2\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} = \sqrt 3 + 2 - \sqrt 3 - 1 = 1\) Chọn A. Câu hỏi 7 : a) Tính chu vi tam giác ABC biết độ dài 3 cạnh là \(AB = 5\sqrt 2 \left( {cm} \right),AC = \sqrt {32} \left( {cm} \right)\), \(BC = \sqrt {98} \left( {cm} \right)\). (Không yêu cầu vẽ hình) b) Thu gọn: \(B = \sqrt {{{\left( {\sqrt 7 - 1} \right)}^2}} - \frac{6}{{\sqrt 7 - 1}}\).
Đáp án: A Phương pháp giải: a) Chu vi tam giác bằng tổng độ dài 3 cạnh của tam giác. Sử dụng công thức \(\sqrt {{a^2}b} = a\sqrt b \left( {a,b \ge 0} \right)\) để rút gọn. b) Sử dụng biểu thức liên hợp để khử căn ở mẫu và công thức \(\sqrt {{a^2}} = |a|\) để phá căn. Lời giải chi tiết: a) Tính chu vi tam giác ABC biết độ dài 3 cạnh là \(AB = 5\sqrt 2 \left( {cm} \right),AC = \sqrt {32} \left( {cm} \right)\), \(BC = \sqrt {98} \left( {cm} \right)\). (Không yêu cầu vẽ hình) Chu vi của tam giác ABC là: \(\begin{array}{l}AB + AC + BC = 5\sqrt 2 + \sqrt {32} + \sqrt {98} = 5\sqrt 2 + \sqrt {{4^2}.2} + \sqrt {{7^2}.2} \\ = 5\sqrt 2 + 4\sqrt 2 + 7\sqrt 2 = 16\sqrt 2 .\end{array}\) Vậy tam giác có chu vi là \(16\sqrt 2 \).\(\) b) Thu gọn: \(B = \sqrt {{{\left( {\sqrt 7 - 1} \right)}^2}} - \frac{6}{{\sqrt 7 - 1}}\). \(\begin{array}{l}B = \sqrt {{{\left( {\sqrt 7 - 1} \right)}^2}} - \frac{6}{{\sqrt 7 - 1}} = \left| {\sqrt 7 - 1} \right| - \frac{{6\left( {\sqrt 7 + 1} \right)}}{{\left( {\sqrt 7 - 1} \right)\left( {\sqrt 7 + 1} \right)}}\\\;\;\; = \sqrt 7 - 1 - \frac{{6\left( {\sqrt 7 + 1} \right)}}{{{{\left( {\sqrt 7 } \right)}^2} - 1}} = \sqrt 7 - 1 - \left( {\sqrt 7 + 1} \right) = \sqrt 7 - 1 - \sqrt 7 - 1 = - 2.\end{array}\) Vậy \(B = - 2\). Chọn A. Câu hỏi 8 : Thực hiện phép tính (thu gọn): Câu 1: \(2\sqrt {48} + \frac{1}{3}\sqrt {108} - 5\sqrt 3 - 3\sqrt {27} \).
Đáp án: A Phương pháp giải: Áp dụng công thức \(\sqrt {{a^2}b} = a\sqrt b \left( {a,b \ge 0} \right)\). Lời giải chi tiết: \(\begin{array}{l}2\sqrt {48} + \frac{1}{3}\sqrt {108} - 5\sqrt 3 - 3\sqrt {27} \\ = 2.\sqrt {{4^2}.3} + \frac{1}{3}\sqrt {{6^2}.3} - 5\sqrt 3 - 3.\sqrt {{3^2}.3} \\ = 8\sqrt 3 + 2\sqrt 3 - 5\sqrt 3 - 9\sqrt 3 = - 4\sqrt 3 \end{array}\) Vậy \(2\sqrt {48} + \frac{1}{3}\sqrt {108} - 5\sqrt 3 - 3\sqrt {27} = - 4\sqrt 3 \). Chọn A. Câu 2: \(\frac{{6 - \sqrt 6 }}{{\sqrt 6 - 1}} - 9\sqrt {\frac{2}{3}} - \frac{4}{{2 - \sqrt 6 }}\).
Đáp án: B Phương pháp giải: Sử dụng biểu thức liên hợp, phân tích tử số để triệt tiêu với mẫu số. Lời giải chi tiết: \(\begin{array}{l}\frac{{6 - \sqrt 6 }}{{\sqrt 6 - 1}} - 9\sqrt {\frac{2}{3}} - \frac{4}{{2 - \sqrt 6 }}\\ = \frac{{\sqrt 6 .\sqrt 6 - \sqrt 6 }}{{\sqrt 6 - 1}} - 3.{\left( {\sqrt 3 } \right)^2}\frac{{\sqrt 2 }}{{\sqrt 3 }} - \frac{{4\left( {2 + \sqrt 6 } \right)}}{{\left( {2 - \sqrt 6 } \right)\left( {2 + \sqrt 6 } \right)}}\\ = \frac{{\sqrt 6 \left( {\sqrt 6 - 1} \right)}}{{\sqrt 6 - 1}} - 3.\sqrt 3 .\sqrt 2 - \frac{{4\left( {2 + \sqrt 6 } \right)}}{{{2^2} - {{\left( {\sqrt 6 } \right)}^2}}} = \sqrt 6 - 3\sqrt 6 - \frac{{4\left( {2 + \sqrt 6 } \right)}}{{ - 2}}\\ = - 2\sqrt 6 + 2\left( {2 + \sqrt 6 } \right) = 4\end{array}\). Vậy \(\frac{{6 - \sqrt 6 }}{{\sqrt 6 - 1}} - 9\sqrt {\frac{2}{3}} - \frac{4}{{2 - \sqrt 6 }} = 4\). Chọn B. Câu hỏi 9 : Tính Câu 1: \(4\sqrt {12} - 15\sqrt {\frac{1}{3}} - \frac{{9 - \sqrt 3 }}{{\sqrt 3 }}\)
Đáp án: A Phương pháp giải: Áp dụng công thức: \(\left\{ \begin{array}{l}\sqrt {a.b} = \sqrt a .\sqrt b \\a.b = a.\sqrt b .\sqrt b \\\sqrt {{a^2}b} = \left| a \right|\sqrt b \end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}a)\;4\sqrt {12} - 15\sqrt {\frac{1}{3}} - \frac{{9 - \sqrt 3 }}{{\sqrt 3 }} = 4\sqrt {{2^2}.3} - \frac{{15}}{{\sqrt 3 }} - \frac{{\sqrt 3 \left( {3\sqrt 3 - 1} \right)}}{{\sqrt 3 }}\\ = 8\sqrt 3 - 5\sqrt 3 - 3\sqrt 3 + 1 = 1.\end{array}\) Vậy \(4\sqrt {12} - 15\sqrt {\frac{1}{3}} - \frac{{9 - \sqrt 3 }}{{\sqrt 3 }} = 1\). Câu 2: \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt {\frac{8}{{7 - 3\sqrt 5 }}} \).
Đáp án: C Phương pháp giải: Áp dụng công thức \(\sqrt {{a^2}} = |a|\) Lời giải chi tiết: \(\begin{array}{l}b)\;\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt {\frac{8}{{7 - 3\sqrt 5 }}} = \left| {2 - \sqrt 5 } \right| - \sqrt {\frac{{16}}{{14 - 6\sqrt 5 }}} \\ = \sqrt 5 - 2 - \frac{{\sqrt {16} }}{{\sqrt {14 - 6\sqrt 5 } }}\;\;\;\left( {do\;\;2 - \sqrt 5 < 0} \right)\\ = \sqrt 5 - 2 - \frac{4}{{\sqrt {{3^2} - 2.3.\sqrt 5 + {{\left( {\sqrt 5 } \right)}^2}} }} = \sqrt 5 - 2 - \frac{4}{{\sqrt {{{\left( {3 - \sqrt 5 } \right)}^2}} }}\\ = \sqrt 5 - 2 - \frac{4}{{\left| {3 - \sqrt 5 } \right|}} = \sqrt 5 - 2 - \frac{4}{{3 - \sqrt 5 }}\;\;\left( {do\;\;3 - \sqrt 5 > 0} \right)\\ = \sqrt 5 - 2 - \frac{{4\left( {3 + \sqrt 5 } \right)}}{{{3^2} - {{\left( {\sqrt 5 } \right)}^2}}} = \sqrt 5 - 2 - \frac{{4\left( {3 + \sqrt 5 } \right)}}{4}\\ = \sqrt 5 - 2 - 3 - \sqrt 5 = - 5.\end{array}\) Vậy \(\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} - \sqrt {\frac{8}{{7 - 3\sqrt 5 }}} = - 5\) Câu hỏi 10 : Thực hiện phép tính: Câu 1: \(3\sqrt {80} - 2\sqrt {45} - \sqrt {125} \)
Đáp án: A Phương pháp giải: Áp dụng công thức \(\sqrt {{a^2}b} = a\sqrt b \left( {a,b \ge 0} \right)\) Lời giải chi tiết: \(\begin{array}{l}3\sqrt {80} - 2\sqrt {45} - \sqrt {125} = 3.\sqrt {{4^2}.5} - 2.\sqrt {{3^2}.5} - \sqrt {{5^2}.5} \\ = 12\sqrt 5 - 6\sqrt 5 - 5\sqrt 5 = \sqrt 5 \end{array}\). Vậy \(3\sqrt {80} - 2\sqrt {45} - \sqrt {125} = \sqrt 5 \). Chọn A. Câu 2: \(\frac{3}{{\sqrt 7 - 1}} - \frac{{\sqrt 7 - \sqrt {21} }}{{2 - 2\sqrt 3 }}\)
Đáp án: A Phương pháp giải: Sử dụng biểu thức liên hợp để khử căn ở mẫu ở phân thức thứ nhất, rút gọn tử và mẫu ở phân thức thứ hai, sau đó tiến hành rút gọn Lời giải chi tiết: \(\begin{array}{l}\frac{3}{{\sqrt 7 - 1}} - \frac{{\sqrt 7 - \sqrt {21} }}{{2 - 2\sqrt 3 }} = \frac{{3.\left( {\sqrt 7 + 1} \right)}}{{\left( {\sqrt 7 - 1} \right).\left( {\sqrt 7 + 1} \right)}} - \frac{{\sqrt 7 - \sqrt 7 .\sqrt 3 }}{{2.\left( {1 - \sqrt 3 } \right)}}\\ = \frac{{3\left( {\sqrt 7 + 1} \right)}}{{{{\left( {\sqrt 7 } \right)}^2} - 1}} - \frac{{\sqrt 7 \left( {1 - \sqrt 3 } \right)}}{{2\left( {1 - \sqrt 3 } \right)}}\\ = \frac{{3\left( {\sqrt 7 + 1} \right)}}{6} - \frac{{\sqrt 7 }}{2} = \frac{{\sqrt 7 + 1}}{2} - \frac{{\sqrt 7 }}{2} = \frac{1}{2}\end{array}\) Vậy \(\frac{3}{{\sqrt 7 - 1}} - \frac{{\sqrt 7 - \sqrt {21} }}{{2 - 2\sqrt 3 }} = \frac{1}{2}\). Chọn A. Câu 3: \(\sqrt {{{\left( {2\sqrt 5 - 5} \right)}^2}} + \sqrt {24 - 8\sqrt 5 } \)
Đáp án: D Phương pháp giải: Tách bên trong căn thức thứ hai thành hằng đẳng thức để khử dấu căn, áp dụng công thức \(\sqrt {{a^2}} = |a|\). Lời giải chi tiết: \(\begin{array}{l}\sqrt {{{\left( {2\sqrt 5 - 5} \right)}^2}} + \sqrt {24 - 8\sqrt 5 } = \sqrt {{{\left( {2\sqrt 5 - 5} \right)}^2}} + \sqrt {{2^2} - 2.2.\left( {2\sqrt 5 } \right) + {{\left( {2\sqrt 5 } \right)}^2}} \\ = \sqrt {{{\left( {2\sqrt 5 - 5} \right)}^2}} + \sqrt {{{\left( {2 - 2\sqrt 5 } \right)}^2}} = \left| {2\sqrt 5 - 5} \right| + \left| {2 - 2\sqrt 5 } \right| = 5 - 2\sqrt 5 + 2\sqrt 5 - 2 = 3\end{array}\) Vậy \(\sqrt {{{\left( {2\sqrt 5 - 5} \right)}^2}} + \sqrt {24 - 8\sqrt 5 } = 3\). Chọn D. Câu hỏi 11 : Thực hiện phép tính: Câu 1: \(A = 3\sqrt {32} - 6\sqrt 2 - \sqrt {50} \)
Đáp án: D Phương pháp giải: Áp dụng công thức: \(\sqrt {{a^2}b} = a\sqrt b \left( {a,b \ge 0} \right)\) Lời giải chi tiết: )\(A = 3\sqrt {32} - 6\sqrt 2 - \sqrt {50} \) \(A = 3\sqrt {32} - 6\sqrt 2 - \sqrt {50} = 3.\sqrt {{4^2}.2} - 6\sqrt 2 - \sqrt {{5^2}.2} = 3.4\sqrt 2 - 6\sqrt 2 - 5\sqrt 2 = \sqrt 2 \) Vậy \(A = \sqrt 2 \) Chọn D Câu 2: \(B = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} \)
Đáp án: B Phương pháp giải: Áp dụng công thức \(\sqrt {{a^2}} = |a|\)Với \(a \in \,R\) Lời giải chi tiết: \(B = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} \) \(B = \sqrt {{{\left( {5 + \sqrt 3 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} = \left| {5 + \sqrt 3 } \right| + \left| {2 - \sqrt 3 } \right| = 5 + \sqrt 3 + 2 - \sqrt 3 = 7\) Vậy \(B = 7\) Chọn B Câu hỏi 12 : Rút gọn biểu thức sau: Câu 1: \(C = \frac{{\sqrt {14} + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 \)
Đáp án: A Phương pháp giải: Áp dụng công thức \(\sqrt {a.b} = \sqrt a .\sqrt b \left( {a,b \ge 0} \right)\). Quan sát biểu thức ta thấy ở tử số có \(\sqrt 7 \) chung. Nếu nhóm làm nhân tử chung ta sẽ thấy xuất hiện nhân tử \(\sqrt 2 + 1\) giống với mẫu số \( \Rightarrow \) có thể rút gọn được. \(\) Lời giải chi tiết: \(C = \frac{{\sqrt {14} + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 \) \(C = \frac{{\sqrt {14} + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 = \frac{{\sqrt 7 .\sqrt 2 + \sqrt 7 }}{{\sqrt 2 + 1}} - \sqrt 7 = \frac{{\sqrt 7 \left( {\sqrt 2 + 1} \right)}}{{\sqrt 2 + 1}} - \sqrt 7 = \sqrt 7 - \sqrt 7 = 0\) Vậy \(C = 0\) Chọn A Câu 2: \(D = \left( {4 - \sqrt {15} } \right){\left( {\sqrt {2 - \sqrt 3 } + \sqrt {3 + \sqrt 5 } } \right)^2}\)
Đáp án: B Phương pháp giải: Nhân biểu thức với 4 rồi lại chia cho 4 để làm xuất hiện các hằng đẳng thức, từ đó phá được căn và rút gọn. Lời giải chi tiết: \(D = \left( {4 - \sqrt {15} } \right){\left( {\sqrt {2 - \sqrt 3 } + \sqrt {3 + \sqrt 5 } } \right)^2}\) \(\begin{array}{l}D = \left( {4 - \sqrt {15} } \right){\left( {\sqrt {2 - \sqrt 3 } + \sqrt {3 + \sqrt 5 } } \right)^2} = \frac{1}{4}.\left[ {2.\left( {4 - \sqrt {15} } \right)} \right].\left[ {{{\left( {\sqrt 2 } \right)}^2}{{\left( {\sqrt {2 - \sqrt 3 } + \sqrt {3 + \sqrt 5 } } \right)}^2}} \right]\\ = \frac{1}{4}\left( {8 - 2\sqrt {15} } \right){\left( {\sqrt {4 - 2\sqrt 3 } + \sqrt {6 + 2\sqrt 5 } } \right)^2}\\ = \frac{1}{4}.\left[ {{{\left( {\sqrt 3 } \right)}^2} - 2\sqrt 3 .\sqrt 5 + {{\left( {\sqrt 5 } \right)}^2}} \right].{\left( {\sqrt {{{\left( {\sqrt 3 } \right)}^2} - 2\sqrt 3 + 1} + \sqrt {{{\left( {\sqrt 5 } \right)}^2} + 2\sqrt 5 + 1} } \right)^2}\\ = \frac{1}{4}{\left( {\sqrt 5 - \sqrt 3 } \right)^2}.{\left( {\sqrt {{{\left( {\sqrt 3 - 1} \right)}^2}} + \sqrt {{{\left( {\sqrt 5 + 1} \right)}^2}} } \right)^2}\\ = \frac{1}{4}{\left( {\sqrt 5 - \sqrt 3 } \right)^2}.{\left( {\left| {\sqrt 3 - 1} \right| + \left| {\sqrt 5 + 1} \right|} \right)^2} = \frac{1}{4}{\left( {\sqrt 5 - \sqrt 3 } \right)^2}{\left( {\sqrt 5 + \sqrt 3 } \right)^2}\\ = \frac{1}{4}{\left( {{{\left( {\sqrt 5 } \right)}^2} - {{\left( {\sqrt 3 } \right)}^2}} \right)^2} = \frac{1}{4}{.2^2} = 1\end{array}\) Vậy \(D = 1\) Chọn B Câu hỏi 13 : Tính Câu 1: \(3\sqrt {18} - \sqrt {32} + 4\sqrt 2 + \sqrt {162} \)
Đáp án: B Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l}\,\,\,3\sqrt {18} - \sqrt {32} + 4\sqrt 2 + \sqrt {162} \\ = 3\sqrt {{3^2}.2} - \sqrt {{4^2}.2} + 4\sqrt 2 + \sqrt {{9^2}.2} \\ = 9\sqrt 2 - 4\sqrt 2 + 4\sqrt 2 + 9\sqrt 2 \\ = 18\sqrt 2 .\end{array}\) Câu 2: \(2\sqrt {48} - 4\sqrt {27} + \sqrt {75} + \sqrt {12} \)
Đáp án: A Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l}\,\,2\sqrt {48} - 4\sqrt {27} + \sqrt {75} + \sqrt {12} \\ = 2\sqrt {{4^2}.3} - 4\sqrt {{3^2}.3} + \sqrt {{5^2}.3} + \sqrt {{2^2}.3} \\ = 8\sqrt 3 - 12\sqrt 3 + 5\sqrt 3 + 2\sqrt 3 \\ = 3\sqrt 3 \end{array}\) Câu 3: \(\sqrt {21 + 8\sqrt 5 } + \sqrt {21 - 8\sqrt 5 } \)
Đáp án: D Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l}\,\,\sqrt {21 + 8\sqrt 5 } + \sqrt {21 - 8\sqrt 5 } \\ = \sqrt {16 + 2.4.\sqrt 5 + 5} + \sqrt {16 - 2.4.\sqrt 5 + 5} \\ = \sqrt {{4^2} + 2.4.\sqrt 5 + {{(\sqrt 5 )}^2}} + \sqrt {{4^2} - 2.4.\sqrt 5 + {{(\sqrt 5 )}^2}} \\ = \sqrt {{{(4 + \sqrt 5 )}^2}} + \sqrt {{{(4 - \sqrt 5 )}^2}} \\ = \left| {4 + \sqrt 5 } \right| + \left| {4 - \sqrt 5 } \right|\\ = 8.\end{array}\) Câu 4: \(\frac{{5\sqrt 2 - 2\sqrt 5 }}{{\sqrt 5 - \sqrt 2 }} - \frac{9}{{\sqrt {10} + 1}}\)
Đáp án: C Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l}\,\,\frac{{5\sqrt 2 - 2\sqrt 5 }}{{\sqrt 5 - \sqrt 2 }} - \frac{9}{{\sqrt {10} + 1}}\\ = \frac{{\sqrt 5 .\sqrt 2 .(\sqrt 5 - \sqrt 2 )}}{{\sqrt 5 - \sqrt 2 }} - \frac{{9(\sqrt {10} - 1)}}{{10 - 1}}\\ = \sqrt {10} - (\sqrt {10} - 1)\\ = 1.\end{array}\) Câu hỏi 14 : Rút gọn biểu thức: \(A = \frac{{3\sqrt {18} - 2\sqrt 8 }}{{\sqrt {50} }}.\)
Đáp án: A Phương pháp giải: Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,\,khi\,\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: Rút gọn biểu thức: \(A = \frac{{3\sqrt {18} - 2\sqrt 8 }}{{\sqrt {50} }}.\) \(A = \frac{{3\sqrt {18} - 2\sqrt 8 }}{{\sqrt {50} }} = \frac{{3\sqrt {{3^2}.2} - 2\sqrt {{2^2}.2} }}{{\sqrt {{5^2}.2} }} = \frac{{9\sqrt 2 - 4\sqrt 2 }}{{5\sqrt 2 }} = \frac{{5\sqrt 2 }}{{5\sqrt 2 }} = 1.\) Vậy \(A = 1.\) Chọn A. Câu hỏi 15 : Tính giá trị biểu thức \(A = \sqrt {1\frac{9}{{16}}.5\frac{4}{9}.0,01} \).
Đáp án: B Phương pháp giải: Quy tắc đổi hỗn số ra phân số: \(a\frac{b}{c} = \frac{{a.c + b}}{c}\) và quy tắc đưa thừa số ra ngoài dấu căn \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,\,A \ge 0\\ - A\,\,khi\,\,A < 0\end{array} \right..\) Lời giải chi tiết: Tính giá trị biểu thức \(A = \sqrt {1\frac{9}{{16}}.5\frac{4}{9}.0,01} \). \(\begin{array}{l}A = \sqrt {1\frac{9}{{16}}.5\frac{4}{9}.0,01} = \sqrt {\frac{{16.1 + 9}}{{16}}.\frac{{9.5 + 4}}{9}.\frac{1}{{100}}} = \sqrt {\frac{{25}}{{16}}.\frac{{49}}{9}.\frac{1}{{100}}} \\\,\,\,\,\, = \sqrt {{{\left( {\frac{5}{4}} \right)}^2}.{{\left( {\frac{7}{3}} \right)}^2}.{{\left( {\frac{1}{{10}}} \right)}^2}} = \left| {\frac{5}{4}.\frac{7}{3}.\frac{1}{{10}}} \right| = \frac{7}{{24}}.\end{array}\). Vậy \(A = \frac{7}{{24}}\). Chọn B. Câu hỏi 16 : Rút gọn: \(\begin{array}{l}a)\,\,\,A = \left( {x - y} \right)\sqrt {\frac{3}{{y - x}}} \\b)\,\,B = 2\sqrt {3x} - \sqrt {48x} + \sqrt {108x} + \sqrt {3x} \,\,\,\,\,\left( {x \ge 0} \right)\\c)\,\,\,C = \frac{1}{{1 - 5x}}\sqrt {3{x^2}\left( {25{x^2} - 10x + 1} \right)} ,\,\,\,0 \le x \le \frac{1}{5}\\d)\,\,D = 2\sqrt {25xy} + \sqrt {225{x^3}{y^3}} - 3y\sqrt {16{x^3}y} \,\,\,\,\left( {x \ge 0,\,\,y \ge 0} \right).\end{array}\)
Đáp án: A Phương pháp giải: Lời giải chi tiết: \(a)\,\,\,A = \left( {x - y} \right)\sqrt {\frac{3}{{y - x}}} \) Điều kiện: \(\frac{3}{{y - x}} > 0 \Leftrightarrow y - x > 0 \Leftrightarrow x < y \Rightarrow x - y < 0.\) \( \Rightarrow A = \left( {x - y} \right)\sqrt {\frac{3}{{y - x}}} = - \sqrt {\frac{{3{{\left( {y - x} \right)}^2}}}{{y - x}}} = - \sqrt {3\left( {y - x} \right)} .\) \(\begin{array}{l}b)\,\,B = 2\sqrt {3x} - \sqrt {48x} + \sqrt {108x} + \sqrt {3x} \,\,\,\,\left( {x \ge 0} \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = 2\sqrt {3x} - \sqrt {{4^2}.3x} + \sqrt {{6^2}.3x} + \sqrt {3x} \\\,\,\,\,\,\,\,\,\,\,\,\, = 2\sqrt {3x} - 4\sqrt {3x} + 6\sqrt {3x} + \sqrt {3x} \\\,\,\,\,\,\,\,\,\,\,\,\, = 5\sqrt {3x} .\,\end{array}\) \(\begin{array}{l}c)\,\,C = \frac{1}{{1 - 5x}}\sqrt {3{x^2}\left( {25{x^2} - 10x + 1} \right)} ,\,\,\,\,0 \le x \le \frac{1}{5}\\\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{{1 - 5x}}\sqrt {3{x^2}{{\left( {5x - 1} \right)}^2}} = \frac{{\sqrt 3 \left| x \right|\left| {5x - 1} \right|}}{{1 - 5x}}\end{array}\) Vì \(x \ge 0 \Rightarrow \left| x \right| = x;\,\,\,0 \le x \le \frac{1}{5} \Rightarrow 5x - 1 \le 0 \Rightarrow \left| {5x - 1} \right| = 1 - 5x.\) \( \Rightarrow C = \frac{{\sqrt 3 x\left( {1 - 5x} \right)}}{{1 - 5x}} = \sqrt 3 x.\) \(\begin{array}{l}d)\,\,D = 2\sqrt {25xy} + \sqrt {225{x^3}{y^3}} - 3y\sqrt {16{x^3}y} \,\,\,\,\left( {x \ge 0,\,\,y \ge 0} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 2\sqrt {{5^2}xy} + \sqrt {{{15}^2}{x^3}{y^3}} - 3y\sqrt {{4^2}{x^3}y} \\\,\,\,\,\,\,\,\,\,\,\,\,\, = 10\sqrt {xy} + 15\left| {xy} \right|\sqrt {xy} - 12\left| x \right|y\sqrt {xy} \\\,\,\,\,\,\,\,\,\,\,\,\,\, = 10\sqrt {xy} + 15xy\sqrt {xy} - 12xy\sqrt {xy} \,\,\,\,\left( {do\,\,\,x \ge 0,\,\,y \ge 0} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 10\sqrt {xy} + 3xy\sqrt {xy} \\\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {xy} \left( {10 + 3xy} \right).\end{array}\) Câu hỏi 17 : Rút gọn biểu thức: \(M = \frac{{3\sqrt {75} - 12\sqrt 3 + \sqrt {12} }}{5}.\)
Đáp án: B Phương pháp giải: Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}M = \frac{{3\sqrt {75} - 12\sqrt 3 + \sqrt {12} }}{5} = \frac{{3\sqrt {{5^2}.3} - 12\sqrt 3 + \sqrt {{2^2}.3} }}{5}\\\,\,\,\,\,\,\,\, = \frac{{3.5\sqrt 3 - 12\sqrt 3 + 2\sqrt 3 }}{5} = \frac{{5\sqrt 3 }}{5} = \sqrt 3 .\end{array}\) Chọn B. Câu hỏi 18 : Chọn đáp án đúng nhất: Câu 1: Tính: \(A = \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} + 1.\) \(B = \left( {2\sqrt 3 + \sqrt {20} } \right)\sqrt 3 - \sqrt {60} .\)
Đáp án: B Phương pháp giải: Sử dụng công thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,khi\,\,A \ge 0\\ - A\,\,khi\,\,A < 0\end{array} \right.\) Lời giải chi tiết: \(A = \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} + 1 = \left| {\sqrt 5 - 1} \right| + 1 = \sqrt 5 - 1 + 1 = \sqrt 5 \,\,\,\,\left( {do\,\,\,\sqrt 5 - 1 > 0} \right).\) \(B = \left( {2\sqrt 3 + \sqrt {20} } \right)\sqrt 3 - \sqrt {60} = 2.3 + \sqrt {20.3} - \sqrt {60} = 6 + \sqrt {60} - \sqrt {60} = 6\) Vậy \(A = \sqrt 5 \,;\,\,\,\,B = 6.\) Chọn B. Câu 2: Cho biểu thức: \(P = \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{1 - \sqrt x }} + \frac{{\sqrt x }}{{\sqrt x + 1}}\) với \(x \ge 0;x \ne 1\). a) Rút gọn \(P.\) b) Tìm \(x\) để \(P = 3\).
Đáp án: D Phương pháp giải: a) Quy đồng mẫu các phân thức sau đó biến đổi và rút gọn phân thức. b) Nhân chéo để rút gọn và tìm biến x, sau đó đối chiếu với điều kiện xác định . Lời giải chi tiết: a) Rút gọn \(P.\) Điều kiện: \(x \ge 0;x \ne 1\). \(\begin{array}{l}P = \frac{{2\sqrt x }}{{x - 1}} - \frac{1}{{1 - \sqrt x }} + \frac{{\sqrt x }}{{\sqrt x + 1}}\\\,\,\,\, = \frac{{2\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{1}{{\sqrt x - 1}} + \frac{{\sqrt x }}{{\sqrt x + 1}}\\\,\,\,\, = \frac{{2\sqrt x + \left( {\sqrt x + 1} \right) + \sqrt x \left( {\sqrt x - 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\\,\,\,\, = \frac{{2\sqrt x + \sqrt x + 1 + x - \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\,\,\,\, = \,\,\,\,\frac{{x + 2\sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\\\,\,\,\, = \frac{{{{\left( {\sqrt x + 1} \right)}^2}}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\,\,\,\,\, = \,\,\,\,\frac{{\sqrt x + 1}}{{\sqrt x - 1}}.\end{array}\) Vậy \(P = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\) với \(x \ge 0;x \ne 1\). b) Tìm \(x\) để \(P = 3\). Ta có: \(P = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\) với \(x \ge 0;x \ne 1\). \(\begin{array}{l}P = 3\, \Rightarrow \frac{{\sqrt x + 1}}{{\sqrt x - 1}} = 3 \Rightarrow \sqrt x + 1 = 3\left( {\sqrt x - 1} \right)\\ \Leftrightarrow \sqrt x + 1 = 3\sqrt x - 3 \Leftrightarrow 2\sqrt x = 4\\ \Leftrightarrow \sqrt x = 2 \Leftrightarrow x = 4\,\,\,\,\left( {tmdk} \right)\end{array}\) Vậy \(x = 4\) thì \(P = 3\). Chọn D. Câu hỏi 19 : Rút gọn các biểu thức: Câu 1: \(A = \frac{1}{{2 - \sqrt 3 }} + \frac{1}{{2 + \sqrt 3 }}\)
Đáp án: D Phương pháp giải: Quy đồng mẫu của các biểu thức để rút gọn Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\;\,khi\,\,A \ge 0\\ - A\sqrt B \,\;\,khi\,\,A < 0\end{array} \right..\) Phân tích đa thức trên tử số thành nhân tử và rút gọn với mẫu số. Lời giải chi tiết: \(A = \frac{1}{{2 - \sqrt 3 }} + \frac{1}{{2 + \sqrt 3 }} = \frac{{2 + \sqrt 3 + 2 - \sqrt 3 }}{{\left( {2 - \sqrt 3 } \right)\left( {2 + \sqrt 3 } \right)}} = \frac{4}{{{2^2} - 3}} = 4\) Vậy \(A = 4.\) Chọn D. Câu 2: \(B = \sqrt {5 + 2\sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} } \)
Đáp án: B Phương pháp giải: Quy đồng mẫu của các biểu thức để rút gọn Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\;\,khi\,\,A \ge 0\\ - A\sqrt B \,\;\,khi\,\,A < 0\end{array} \right..\) Phân tích đa thức trên tử số thành nhân tử và rút gọn với mẫu số. Lời giải chi tiết: \(\begin{array}{l}B = \sqrt {5 + 2\sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} } = \sqrt {5 + 2.\left( {\sqrt 2 - 1} \right)} \\\,\,\,\,\, = \sqrt {5 + 2\sqrt 2 - 2} = \sqrt {3 + 2\sqrt 2 } \\\,\,\,\,\, = \sqrt {{{\left( {\sqrt 2 + 1} \right)}^2}} = \sqrt 2 + 1.\end{array}\) Vậy \(B = \sqrt 2 + 1.\) Chọn B. Câu 3: \(C = \frac{{x + \sqrt x - 2}}{{\sqrt x + 2}}\) (với \(x \ge 0\))
Đáp án: B Phương pháp giải: Quy đồng mẫu của các biểu thức để rút gọn Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\;\,khi\,\,A \ge 0\\ - A\sqrt B \,\;\,khi\,\,A < 0\end{array} \right..\) Phân tích đa thức trên tử số thành nhân tử và rút gọn với mẫu số. Lời giải chi tiết: \(\begin{array}{l}C = \frac{{x + \sqrt x - 2}}{{\sqrt x + 2}}\,\,\,\left( {x \ge 0} \right)\\\,\,\,\,\, = \frac{{x + 2\sqrt x - \sqrt x - 2}}{{\sqrt x + 2}} = \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 1} \right)}}{{\sqrt x + 2}} = \sqrt x - 1.\end{array}\) Vậy \(C = \sqrt x - 1\) với \(x \ge 0\). Chọn B. Câu hỏi 20 : Chọn đáp án đúng nhất: Câu 1: Thực hiện phép tính: \(3\sqrt {12} + \frac{1}{2}\sqrt {48} - \sqrt {27} \)
Đáp án: C Phương pháp giải: Áp dụng quy tắc phá dấu căn: \(\sqrt {{A^2}.B} = \left[ \begin{array}{l}A.B\,khi\,A \ge 0\\ - A.B\,khi\,A < 0\end{array} \right.\) Lời giải chi tiết: Thực hiện phép tính: \(3\sqrt {12} + \frac{1}{2}\sqrt {48} - \sqrt {27} \) \(\begin{array}{l}3\sqrt {12} + \frac{1}{2}\sqrt {48} - \sqrt {27} = 3\sqrt {4.3} + \frac{1}{2}\sqrt {16.3} - \sqrt {9.3} = 3.2\sqrt 3 + \frac{1}{2}.4\sqrt 3 - 3\sqrt 3 \\ = 6\sqrt 3 + 2\sqrt 3 - 3\sqrt 3 = 5\sqrt 3 \end{array}\) Chọn C. Câu 2: Trục căn thức ở mẫu: \(\frac{2}{{\sqrt 3 - 5}}\).
Đáp án: A Phương pháp giải: Trục căn thức ở mẫu bằng cách nhân với biểu thức liên hợp Lời giải chi tiết: Trục căn thức ở mẫu: \(\frac{2}{{\sqrt 3 - 5}}\). \(\frac{2}{{\sqrt 3 - 5}} = \frac{{2\left( {\sqrt 3 + 5} \right)}}{{\left( {\sqrt 3 - 5} \right)\left( {\sqrt 3 + 5} \right)}} = \frac{{2\left( {\sqrt 3 + 5} \right)}}{{3 - 25}} = \frac{{2\left( {\sqrt 3 + 5} \right)}}{{ - 22}} = - \frac{{\sqrt 3 + 5}}{{11}}\) Chọn A. Câu 3: Khử mẫu của biểu thức lấy căn \(\sqrt {\frac{2}{5}} \)
Đáp án: D Phương pháp giải: Áp dụng quy tắc phá dấu căn: \(\sqrt {{A^2}.B} = \left[ \begin{array}{l}A.B\,khi\,A \ge 0\\ - A.B\,khi\,A < 0\end{array} \right.\) Lời giải chi tiết: Khử mẫu của biểu thức lấy căn \(\sqrt {\frac{2}{5}} \) \(\sqrt {\frac{2}{5}} = \sqrt {\frac{{2.5}}{{{5^2}}}} = \frac{{\sqrt {10} }}{5}\) Chọn D. Câu hỏi 21 : Chọn đáp án đúng nhất: Câu 1: Không sử dụng máy tính cầm tay, thực hiện phép tính: a) \(A = \sqrt {100} - \sqrt {16} + \sqrt {25} \). b) \(B = \frac{1}{{2 + \sqrt 3 }} - \frac{2}{{2 - \sqrt 3 }}\)
Đáp án: A Phương pháp giải: a) Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}} = \left[ \begin{array}{l}A\,\,\,\,khi\,\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,\,A < 0\end{array} \right..\) b) Quy đồng mẫu số và rút gọn biểu thức. Lời giải chi tiết: \(a)\,\,\,A = \sqrt {100} - \sqrt {16} + \sqrt {25} = \sqrt {{{10}^2}} - \sqrt {{4^2}} + \sqrt {{5^2}} = 10 - 4 + 5 = 11.\) \(b)\,\,\,B = \frac{1}{{2 + \sqrt 3 }} - \frac{2}{{2 - \sqrt 3 }} = \frac{{2 - \sqrt 3 - 2\left( {2 + \sqrt 3 } \right)}}{{\left( {2 + \sqrt 3 } \right)\left( {2 - \sqrt 3 } \right)}} = \frac{{2 - \sqrt 3 - 4 - 2\sqrt 3 }}{{{2^2} - 3}} = \frac{{ - 2 - 3\sqrt 3 }}{{4 - 3}} = - 2 - 3\sqrt 3 \) Chọn A. Câu 2: Tìm các giá trị của \(x\) biết: a) \(\sqrt x - 2 = 0\) b) \(\sqrt {{{\left( {x - 4} \right)}^2}} = 2x + 1\)
Đáp án: D Phương pháp giải: a) Giải phương trình: \(\sqrt A = B\left( {A \ge 0;B \ge 0} \right) \Leftrightarrow A = {B^2}\) b) Giải phương trình: \(\sqrt A = B\,\,\,\left( {A \ge 0;\,\,\,B \ge 0} \right) \Leftrightarrow A = {B^2}\) Lời giải chi tiết: a) \(\sqrt x - 2 = 0\) ĐKXĐ: \(x \ge 0\) \(\sqrt x - 2 = 0 \Leftrightarrow \sqrt x = 2 \Leftrightarrow x = {2^2} \Leftrightarrow x = 4\,\,\,\left( {tmdk} \right)\) Vậy \(x = 4.\) b) \(\sqrt {{{\left( {x - 4} \right)}^2}} = 2x + 1\) ĐKXĐ: \(2x + 1 \ge 0 \Rightarrow x \ge \frac{{ - 1}}{2}\) \(\begin{array}{l}\sqrt {{{\left( {x - 4} \right)}^2}} = 2x + 1 \Leftrightarrow {\left( {x - 4} \right)^2} = {\left( {2x + 1} \right)^2}\\ \Leftrightarrow {x^2} - 8x + 16 = 4{x^2} + 4x + 1\\ \Leftrightarrow 3{x^2} + 12x - 15 = 0\\ \Leftrightarrow {x^2} + 4x - 5 = 0\\ \Leftrightarrow {x^2} + 5x - x - 5 = 0\\ \Leftrightarrow \left( {x + 5} \right)\left( {x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 5 = 0\\x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 5\,\,\,\,\left( {ktm} \right)\\x = 1\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Vậy \(x = 1\). Chọn D. Câu hỏi 22 : Chọn đáp án đúng nhất: Câu 1: Thực hiện phép tính: \(3\sqrt 8 - \sqrt {50} - \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} .\)
Đáp án: A Phương pháp giải: Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\;\,khi\,\,A \ge 0\\ - A\sqrt B \,\;\,khi\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}3\sqrt 8 - \sqrt {50} - \sqrt {{{\left( {\sqrt 2 - 1} \right)}^2}} \\ = 3\sqrt {{2^2}.2} - \sqrt {{5^2}.2} - \left| {\sqrt 2 - 1} \right|\\ = 3.2\sqrt 2 - 5\sqrt 2 - \left( {\sqrt 2 - 1} \right)\\ = 6\sqrt 2 - 5\sqrt 2 - \sqrt 2 + 1\\ = 1\end{array}\) Chọn A. Câu 2: Giải các phương trình sau: a) \(\sqrt {{x^2} - 6x + 9} = 1\) b) \(2\sqrt {12x} - 3\sqrt {3x} + 4\sqrt {48x} = 17.\)
Đáp án: C Phương pháp giải: a) Tìm điều kiện xác định sau đó giải phương trình bằng phương pháp đưa phương trình về dạng \(\left| A \right| = m\,\left( {m \ge 0} \right) \Leftrightarrow \left[ \begin{array}{l}A = m\\A = - m\end{array} \right.\) b) Tìm điều kiện xác định của phương trình sau đó dùng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\;\,khi\,\,A \ge 0\\ - A\sqrt B \,\;\,khi\,\,A < 0\end{array} \right.\) để giải phương trình. Lời giải chi tiết: a) \(\sqrt {{x^2} - 6x + 9} = 1\) Điều kiện xác định: \(x \in \mathbb{R}\) \(({x^2} - 6x + 9 \ge 0 \Leftrightarrow {\left( {x - 3} \right)^2} \ge 0\) đúng với mọi \(x \in \mathbb{R}\,)\) \(\begin{array}{l}\sqrt {{x^2} - 6x + 9} = 1 \Leftrightarrow \sqrt {{{\left( {x - 3} \right)}^2}} = 1\\ \Leftrightarrow \left| {x - 3} \right| = 1 \Leftrightarrow \left[ \begin{array}{l}x - 3 = 1\\x - 3 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 2\end{array} \right.\,\,\,\left( {tmdk} \right)\end{array}\) Vậy \(S = \left\{ {2;4} \right\}.\) b) \(2\sqrt {12x} - 3\sqrt {3x} + 4\sqrt {48x} = 17.\) Điều kiện xác định: \(x \ge 0\) \(\begin{array}{l}2\sqrt {12x} - 3\sqrt {3x} + 4\sqrt {48x} = 17\\ \Leftrightarrow 2\sqrt {{2^2}.3x} - 3\sqrt {3x} + 4\sqrt {{4^2}.3x} = 17\\ \Leftrightarrow 2.2\sqrt {3x} - 3\sqrt {3x} + 4.4\sqrt {3x} = 17\\ \Leftrightarrow 4\sqrt {3x} - 3\sqrt {3x} + 16\sqrt {3x} = 17\\ \Leftrightarrow 17\sqrt {3x} = 17 \Leftrightarrow \sqrt {3x} = 1\\ \Leftrightarrow 3x = 1 \Leftrightarrow x = \frac{1}{3}\,\,\left( {tmdk} \right)\end{array}\) Vậy \(S = \left\{ {\frac{1}{3}} \right\}.\) Chọn C. Câu hỏi 23 : Chọn đáp án đúng nhất: Câu 1: Tính : a) \(\frac{5}{{\sqrt 5 - 1}} - \frac{5}{{\sqrt 5 + 1}};\) b) \(\sqrt {{{\left( {\sqrt 5 - 3} \right)}^2}} - \sqrt {\frac{1}{5}} \)
Đáp án: C Phương pháp giải: a) Quy đồng mẫu số và rút gọn biểu thức. b) Rút gọn căn bậc hai bằng công thức: \(\sqrt {{A^2}} = \left[ \begin{array}{l}A\,\,\,\,khi\,\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,\,A < 0\end{array} \right.\) và \(\sqrt {\frac{1}{A}} = \frac{{\sqrt A }}{A}\,\,\left( {A > 0} \right)\) Lời giải chi tiết: \(\begin{array}{l}a)\,\frac{5}{{\sqrt 5 - 1}} - \frac{5}{{\sqrt 5 + 1}} = \frac{{5\left( {\sqrt 5 + 1} \right) - 5\left( {\sqrt 5 - 1} \right)}}{{\left( {\sqrt 5 + 1} \right)\left( {\sqrt 5 - 1} \right)}}\\ = \frac{{5\sqrt 5 + 5 - 5\sqrt 5 + 5}}{{5 - 1}} = \frac{{10}}{4} = \frac{5}{2}\end{array}\) \(\begin{array}{l}b)\,\sqrt {{{\left( {\sqrt 5 - 3} \right)}^2}} - \sqrt {\frac{1}{5}} = \left| {\sqrt 5 - 3} \right| - \frac{{\sqrt 5 }}{5}\\ = 3 - \sqrt 5 - \frac{{\sqrt 5 }}{5} = \frac{{15 - 5\sqrt 5 - \sqrt 5 }}{5} = \frac{{15 - 6\sqrt 5 }}{5}\end{array}\) Chọn C. Câu 2: Giải các phương trình sau : a) \(\sqrt {x - 1} + \sqrt {9x - 9} + \sqrt {4x - 4} = 12;\) b) \(\sqrt {{x^2} - 5x} - \sqrt {x - 5} = 0\)
Đáp án: D Phương pháp giải: a) Biến đổi đưa về giải phương trình: \(\sqrt A = B\left( {A \ge 0;B \ge 0} \right) \Leftrightarrow A = {B^2}\) b) Giải phương trình: \(\sqrt A = \sqrt B \,\,\,\left( {A \ge 0;\,\,\,B \ge 0} \right) \Leftrightarrow A = B\) Lời giải chi tiết: a) \(\sqrt {x - 1} + \sqrt {9x - 9} + \sqrt {4x - 4} = 12\) ĐKXĐ: \(x - 1 \ge 0 \Leftrightarrow x \ge 1\) \(\begin{array}{l}\sqrt {x - 1} + \sqrt {9x - 9} + \sqrt {4x - 4} = 12\\ \Leftrightarrow \sqrt {x - 1} + \sqrt {9\left( {x - 1} \right)} + \sqrt {4\left( {x - 1} \right)} = 12\\ \Leftrightarrow \sqrt {x - 1} + 3\sqrt {x - 1} + 2\sqrt {x - 1} = 12\\ \Leftrightarrow 6\sqrt {x - 1} = 12\\ \Leftrightarrow \sqrt {x - 1} = 2\\ \Leftrightarrow x - 1 = 4\\ \Leftrightarrow x = 5\left( {tmdk} \right)\end{array}\) Vậy \(x = 5.\) b) \(\sqrt {{x^2} - 5x} - \sqrt {x - 5} = 0\) ĐKXĐ: \(x - 5 \ge 0 \Leftrightarrow x \ge 5\) \(\begin{array}{l}\sqrt {{x^2} - 5x} - \sqrt {x - 5} = 0\\ \Leftrightarrow \sqrt {{x^2} - 5x} = \sqrt {x - 5} \\ \Leftrightarrow {x^2} - 5x = x - 5\\ \Leftrightarrow x\left( {x - 5} \right) - \left( {x - 5} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x - 5 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\left( {ktm} \right)\\x = 5\left( {tm} \right)\end{array} \right.\end{array}\) Vậy \(x = 5\). Chọn D. Câu hỏi 24 : Rút gọn các biểu thức: Câu 1: \(A = 3\sqrt {\frac{1}{3}} + \frac{1}{2}\sqrt {48} + \sqrt {75} \)
Đáp án: D Phương pháp giải: Đưa thừa số ra ngoài dấu căn \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \). Lời giải chi tiết: +) Ta có : \(A = 3\sqrt {\frac{1}{3}} + \frac{1}{2}\sqrt {48} + \sqrt {75} \)\( = 3.\frac{{\sqrt 3 }}{3} + \frac{1}{2}.4\sqrt 3 + 5\sqrt 3 \) \( = \sqrt 3 + 2\sqrt 3 + 5\sqrt 3 = 8\sqrt 3 \) Chọn D. Câu 2: \(B = 3\sqrt {20} - 20\sqrt {\frac{1}{5}} - \frac{4}{{\sqrt 5 + \sqrt 3 }}\)
Đáp án: C Phương pháp giải: Đưa thừa số ra ngoài dấu căn \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \). Trục căn thức ở mẫu \(\frac{C}{{\sqrt A + \sqrt B }} = \frac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}}\). Lời giải chi tiết: +) Ta có: \(B = 3\sqrt {20} - 20\sqrt {\frac{1}{5}} - \frac{4}{{\sqrt 5 + \sqrt 3 }}\)\( = 3.2\sqrt 5 - 20.\frac{{\sqrt 5 }}{5} - \frac{{4\left( {\sqrt 5 - \sqrt 3 } \right)}}{{\left( {\sqrt 5 + \sqrt 3 } \right)\left( {\sqrt 5 - \sqrt 3 } \right)}}\) \(B = 6\sqrt 5 - 4\sqrt 5 - \frac{{4\left( {\sqrt 5 - \sqrt 3 } \right)}}{{5 - 3}}\)\( = 2\sqrt 5 - 2\sqrt 5 + 2\sqrt 3 = 2\sqrt 3 \). Chọn C. Câu hỏi 25 : Chọn đáp án đúng nhất: Câu 1: Tính giá trị của biểu thức : \(\sqrt {20} - 3\sqrt 5 + 2\sqrt {45} .\)
Đáp án: D Phương pháp giải: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \,\,\left( {B \ge 0} \right)\) Lời giải chi tiết: Ta có: \(\sqrt {20} - 3\sqrt 5 + 2\sqrt {45} \)\( = \sqrt {4.5} - 3\sqrt 5 + 2\sqrt {9.5} \) \( = 2\sqrt 5 - 3\sqrt 5 + 2.3\sqrt 5 = 2\sqrt 5 - 3\sqrt 5 + 6\sqrt 5 = 5\sqrt 5 \) Chọn D. Câu 2: Tìm \(x,\) biết : \(\sqrt {x - 1} + \sqrt {4x - 4} = 9.\)
Đáp án: D Phương pháp giải: Sử dụng \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \,\,\left( {B \ge 0} \right)\) để đưa về dạng \(\sqrt A = m\left( {m \ge 0} \right) \Leftrightarrow A = {m^2}\,\,\left( {A \ge 0} \right)\) Lời giải chi tiết: Điều kiện: \(x - 1 \ge 0 \Leftrightarrow x \ge 1\) Ta có: \(\sqrt {x - 1} + \sqrt {4x - 4} = 9.\) \(\begin{array}{l} \Leftrightarrow \sqrt {x - 1} + \sqrt {4\left( {x - 1} \right)} = 9\\ \Leftrightarrow \sqrt {x - 1} + 2\sqrt {x - 1} = 9\\ \Leftrightarrow 3\sqrt {x - 1} = 9\\ \Leftrightarrow \sqrt {x - 1} = 3\\ \Leftrightarrow x - 1 = 9\\ \Leftrightarrow x = 10\left( {tm} \right)\end{array}\) Vậy \(x = 10.\) Chọn D. Câu hỏi 26 : Chọn đáp án đúng nhất: Câu 1: Thực hiện phép tính : \(a)\,\,\sqrt {20} - 3\sqrt {125} + 5\sqrt {45} \) \(b)\,\,\frac{3}{{\sqrt 3 - \sqrt 2 }} - 2\sqrt {{{\left( {\sqrt 2 - \sqrt 3 } \right)}^2}} - 5\sqrt 2 \)
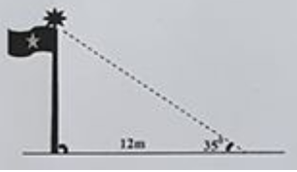
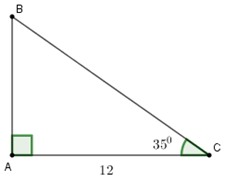
Đáp án: B Phương pháp giải: a) Sử dụng công thức đưa thừa số ra ngoài dấu căn : Với \(B \ge 0\) ta có : \(\sqrt {{A^2}B} = \left| A \right|B = \left\{ \begin{array}{l}AB\,\,\,\,khi\,\,\,\,A \ge 0\\ - AB\,\,\,khi\,\,\,\,A < 0\end{array} \right..\) b) Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\) và trục căn thức ở mẫu : \(\frac{m}{{\sqrt A - \sqrt B }} = \frac{{m\left( {\sqrt A + \sqrt B } \right)}}{{A - B}}\,\,\,\left( {A,B \ge 0;A \ne B} \right)\) Lời giải chi tiết: \(\begin{array}{l}a)\,\,\sqrt {20} - 3\sqrt {125} + 5\sqrt {45} \\ = 2\sqrt 5 - 15\sqrt 5 + 15\sqrt 5 \\ = 2\sqrt 5 \end{array}\) \(\begin{array}{l}b)\,\,\frac{3}{{\sqrt 3 - \sqrt 2 }} - 2\sqrt {{{\left( {\sqrt 2 - \sqrt 3 } \right)}^2}} - 5\sqrt 2 \\ = \frac{{3\left( {\sqrt 3 + \sqrt 2 } \right)}}{{3 - 2}} - 2\left| {\sqrt 2 - \sqrt 3 } \right| - 5\sqrt 2 \\ = 3\sqrt 3 + 3\sqrt 2 - 2\left( {\sqrt 3 - \sqrt 2 } \right) - 5\sqrt 2 \\ = 3\sqrt 3 + 3\sqrt 2 - 2\sqrt 3 + 2\sqrt 2 - 5\sqrt 2 \\ = \sqrt 3 \end{array}\) Chọn B. Câu 2: Một cột cờ vuông góc với mặt đất có bóng dài \(12m\), tia nắng của mặt trời tạo với mặt đất một góc là \(35\) (hình vẽ bên). Tính chiều cao của cột cờ.
Đáp án: C Phương pháp giải: Sử dụng quan hệ giữa cạnh và góc trong tam giác. Trong tam giác vuông, cạnh góc vuông này bằng cạnh góc vuông còn lại nhân tan góc đối. Lời giải chi tiết: Ta đưa về bài toán: Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 12m,\,\,\,\angle BCA = {35^0}.\) Tính \(AB.\) Chiều cao cột là \(AB\). Do \(\Delta ABC\) vuông tại \(A\) nên ta có : \(\begin{array}{l}AB = AC.\tan C\\\,\,\,\,\,\,\,\,\, = 12.\tan 35^\circ \\\,\,\,\,\,\,\,\,\, = 8,402\,\,\left( m \right)\end{array}\) Chọn C. Câu hỏi 27 : Thực hiện phép tính: Câu 1: \( - 3\sqrt {80} + 7\sqrt {45} - \sqrt {500} \)
Đáp án: B Phương pháp giải: Đưa thừa số ra ngoài dấu căn, sử dụng \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \). Lời giải chi tiết: \( - 3\sqrt {80} + 7\sqrt {45} - \sqrt {500} \) \(\begin{array}{l} = - 3\sqrt {16.5} + 7.\sqrt {9.5} - \sqrt {100.5} \\ = - 12\sqrt 5 + 21\sqrt 5 - 10\sqrt 5 \\ = - \sqrt 5 \end{array}\) Chọn B. Câu 2: \(\sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} + \sqrt {19 + 8\sqrt 3 } \)
Đáp án: A Phương pháp giải: Đưa thừa số ra ngoài dấu căn, sử dụng \(\sqrt {{A^2}B} = \left| A \right|\sqrt B \). Lời giải chi tiết: \(\sqrt {{{\left( {\sqrt 3 - 2} \right)}^2}} + \sqrt {19 + 8\sqrt 3 } \) \(\begin{array}{l} = \left| {\sqrt 3 - 2} \right| + \sqrt {{{\left( {4 + \sqrt 3 } \right)}^2}} \\ = 2 - \sqrt 3 + 4 + \sqrt 3 \\ = 6\end{array}\) Chọn A. Câu 3: \(\frac{{\sqrt {14} }}{{\sqrt 7 }} - \frac{5}{{1 + \sqrt 2 }} + \frac{{\sqrt {28} - 2\sqrt 3 }}{{\sqrt 7 - \sqrt 3 }}\)
Đáp án: A Phương pháp giải: Thực hiện rút gọn bằng cách đưa tử và mẫu về dạng tích kết hợp trục căn thức ở mẫu: \(\frac{C}{{\sqrt A + \sqrt B }} = \frac{{C\left( {\sqrt A - \sqrt B } \right)}}{{A - B}}\) Lời giải chi tiết: \(\frac{{\sqrt {14} }}{{\sqrt 7 }} - \frac{5}{{1 + \sqrt 2 }} + \frac{{\sqrt {28} - 2\sqrt 3 }}{{\sqrt 7 - \sqrt 3 }}\) \(\begin{array}{l} = \sqrt 2 - \frac{{5\left( {1 - \sqrt 2 } \right)}}{{1 - 2}} + \frac{{2\left( {\sqrt 7 - \sqrt 3 } \right)}}{{\sqrt 7 - \sqrt 3 }}\\ = \sqrt 2 + 5\left( {1 - \sqrt 2 } \right) + 2\\ = \sqrt 2 + 5 - 5\sqrt 2 + 2\\ = 7 - 4\sqrt 2 \end{array}\) Chọn A. Câu hỏi 28 : Tính giá trị của biểu thức: \(T = \left( {2\sqrt 3 + 1} \right)\left( {3\sqrt 2 - 1} \right)\sqrt {13 - 4\sqrt 3 } \sqrt {19 + 6\sqrt 2 } \)
Đáp án: B Phương pháp giải: - Đưa các biểu thức dưới dấu căn về dạng bình phương, áp dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\). - Nhân thích hợp, sử dụng hằng đẳng thức \(\left( {A - B} \right)\left( {A + B} \right) = {A^2} - {B^2}\). Lời giải chi tiết: \(\begin{array}{l}T = \left( {2\sqrt 3 + 1} \right)\left( {3\sqrt 2 - 1} \right)\sqrt {13 - 4\sqrt 3 } \sqrt {19 + 6\sqrt 2 } \\T = \left( {2\sqrt 3 + 1} \right)\left( {3\sqrt 2 - 1} \right)\sqrt {{{\left( {2\sqrt 3 - 1} \right)}^2}} \sqrt {{{\left( {3\sqrt 2 + 1} \right)}^2}} \\T = \left( {2\sqrt 3 + 1} \right)\left( {2\sqrt 3 - 1} \right)\left( {3\sqrt 2 - 1} \right)\left( {3\sqrt 2 + 1} \right)\\T = 11.17 = 187\end{array}\) Chọn B. Câu hỏi 29 : Tính giá trị của biểu thức \(A = \frac{{{x^4} - 2{x^3} + 3{x^2} - 38x + 5}}{{\sqrt {{x^2} - 4x + 5} }}\) khi \(x = 2 + \sqrt 3 .\)
Đáp án: A Phương pháp giải: Tìm điều kiện xác định, với \(x = 2 + \sqrt 3 \,\,\,\left( {tm} \right),\) ta biến đổi và tính giá trị của biểu thức \(A.\) Lời giải chi tiết: Điều kiện: \(x \in \mathbb{R}.\) Với \(x = 2 + \sqrt 3 \,\,\left( {tm} \right)\) \( \Rightarrow x - 2 = \sqrt 3 \Rightarrow {\left( {x - 2} \right)^2} = 3\)\( \Leftrightarrow {x^2} - 4x + 4 = 3 \Leftrightarrow {x^2} - 4x + 1 = 0\) Mẫu số: \(\sqrt {{x^2} - 4x + 5} = \sqrt {{x^2} - 4x + 1 + 4} = 2\). Tử số: \({x^4} - 2{x^3} + 3{x^2} - 38x + 5\) \(\begin{array}{l} = \left( {{x^4} - 4{x^3} + {x^2}} \right) + \left( {2{x^3} - 8{x^2} + 2x} \right) + \left( {10{x^2} - 40x + 10} \right) - 5\\ = {x^2}\left( {{x^2} - 4x + 1} \right) + 2x\left( {{x^2} - 4x + 1} \right) + 10\left( {{x^2} - 4x + 1} \right) - 5\\ = - 5\end{array}\) \( \Rightarrow A = - \frac{5}{2}\) Chọn A. Câu hỏi 30 : Cho biểu thức \(P = \left( {\frac{1}{{a - 1}} + \frac{{3\sqrt a + 5}}{{a\sqrt a - a - \sqrt a + 1}}} \right).\left( {\frac{{{{\left( {\sqrt a + 1} \right)}^2}}}{{4\sqrt a }} - 1} \right)\) Tìm điều kiện xác định và rút gọn biểu thức \(P.\)
Đáp án: A Phương pháp giải: +) Xác định điều kiện của biểu thức. +) Quy đồng mẫu các phân thức sau đó biến đổi và rút gọn biểu thức. Lời giải chi tiết: \(P = \left( {\frac{1}{{a - 1}} + \frac{{3\sqrt a + 5}}{{a\sqrt a - a - \sqrt a + 1}}} \right).\left( {\frac{{{{\left( {\sqrt a + 1} \right)}^2}}}{{4\sqrt a }} - 1} \right)\) Điều kiện : \( \Leftrightarrow \left\{ \begin{array}{l}a \ge 0\\a - 1 \ne 0\\a\sqrt a - a - \sqrt a + 1 \ne 0\\\sqrt a \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a > 0\\a \ne 1\end{array} \right..\) \(\begin{array}{l}P = \left( {\frac{1}{{a - 1}} + \frac{{3\sqrt a + 5}}{{a\sqrt a - a - \sqrt a + 1}}} \right).\left( {\frac{{{{\left( {\sqrt a + 1} \right)}^2}}}{{4\sqrt a }} - 1} \right)\\ = \left( {\frac{1}{{a - 1}} + \frac{{3\sqrt a + 5}}{{a\left( {\sqrt a - 1} \right) - \left( {\sqrt a - 1} \right)}}} \right).\frac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\ = \left( {\frac{1}{{a - 1}} + \frac{{3\sqrt a + 5}}{{\left( {a - 1} \right)\left( {\sqrt a - 1} \right)}}} \right).\frac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\ = \frac{{\sqrt a - 1 + 3\sqrt a + 5}}{{\left( {a - 1} \right)\left( {\sqrt a - 1} \right)}}.\frac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }}\\ = \frac{{4\left( {\sqrt a + 1} \right)}}{{\left( {\sqrt a + 1} \right){{\left( {\sqrt a - 1} \right)}^2}}}.\frac{{{{\left( {\sqrt a - 1} \right)}^2}}}{{4\sqrt a }} = \frac{1}{{\sqrt a }}.\end{array}\) Chọn A. Câu hỏi 31 : Rút gọn biểu thức \(2\sqrt {8\sqrt 3 } - 2\sqrt {5\sqrt 3 } - 3\sqrt {20\sqrt 3 } \)
Đáp án: B Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}\,\,\,\,\,2\sqrt {8\sqrt 3 } - 2\sqrt {5\sqrt 3 } - 3\sqrt {20\sqrt 3 } \\ = 2\sqrt {4.2} .\sqrt {\sqrt 3 } - 2\sqrt 5 .\sqrt {\sqrt 3 } - 3\sqrt {4.5} .\sqrt {\sqrt 3 } \\ = 2.2\sqrt 2 \sqrt {\sqrt 3 } - 2\sqrt 5 \sqrt {\sqrt 3 } - 3.2.\sqrt 5 .\sqrt {\sqrt 3 } \\ = 4\sqrt {2\sqrt 3 } - \left( {2 + 3.2} \right)\sqrt 5 \sqrt {\sqrt 3 } \\ = 4\sqrt {2\sqrt 3 } - 8\sqrt {5\sqrt 3 } \end{array}\) Chọn B. Câu hỏi 32 : Rút gọn biểu thức \(\left( {4\sqrt x - \sqrt {2x} } \right)\left( {\sqrt x - \sqrt {2x} } \right)\) với \(x\) không âm ta được:
Đáp án: C Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}\,\,\,\left( {4\sqrt x - \sqrt {2x} } \right)\left( {\sqrt x - \sqrt {2x} } \right)\\ = 4\sqrt x .\sqrt x - 4\sqrt {2x.x} - \sqrt {2x.x} + \sqrt {2x} .\sqrt {2x} \\ = 4x - 4\sqrt {2{x^2}} - \sqrt {2{x^2}} + 2x\\ = 6x - 5\sqrt {2{x^2}} \\ = 6x - 5\sqrt 2 \left| x \right|\\ = 6x - 5\sqrt 2 x\,\,\,\left( {do\,\,\,x \ge 0} \right)\\ = \left( {6 - 5\sqrt 2 } \right)x.\end{array}\) Chọn C. Câu hỏi 33 : Rút gọn biểu thức \(A = \sqrt {x + 2\sqrt {2x - 4} } + \sqrt {x - 2\sqrt {2x - 4} } \) với \(x \ge 2\) ta được:
Đáp án: A Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Áp dụng hằng đẳng thức đáng nhớ để xử lý bài toán: \({\left( {A \pm B} \right)^2} = {A^2} \pm 2AB + {B^2}\) Lời giải chi tiết: Điều kiện: \(x \ge 2\) \(\begin{array}{l}A = \sqrt {x + 2\sqrt {2x - 4} } + \sqrt {x - 2\sqrt {2x - 4} } \\ = \sqrt {x + 2\sqrt {2\left( {x - 2} \right)} } + \sqrt {x - 2\sqrt {2\left( {x - 2} \right)} } \\ = \sqrt {x - 2 + 2\sqrt 2 .\sqrt {x - 2} + 2} + \sqrt {x - 2 - 2\sqrt 2 .\sqrt {x - 2} + 2} \\ = \sqrt {{{\left( {\sqrt {x - 2} + \sqrt 2 } \right)}^2}} + \sqrt {{{\left( {\sqrt {x - 2} - \sqrt 2 } \right)}^2}} \\ = \left| {\sqrt {x - 2} + \sqrt 2 } \right| + \left| {\sqrt {x - 2} - \sqrt 2 } \right|\\ = \sqrt {x - 2} + \sqrt 2 + \left| {\sqrt {x - 2} - \sqrt 2 } \right|\,\,\,\end{array}\) +) Với \(\sqrt {x - 2} - \sqrt 2 \ge 0 \Leftrightarrow \sqrt {x - 2} \ge \sqrt 2 \) \( \Leftrightarrow x - 2 \ge 2 \Leftrightarrow x \ge 4\) ta có: \(\left| {\sqrt {x - 2} - \sqrt 2 } \right| = \sqrt {x - 2} - \sqrt 2 \) \( \Rightarrow A = \sqrt {x - 2} + \sqrt 2 + \sqrt {x - 2} - \sqrt 2 \) \( = 2\sqrt {x - 2} .\) +) Với \(\sqrt {x - 2} - \sqrt 2 < 0 \Leftrightarrow \sqrt {x - 2} < \sqrt 2 \) \( \Leftrightarrow x - 2 < 2 \Leftrightarrow x < 4\) ta có: \(\left| {\sqrt {x - 2} - \sqrt 2 } \right| = \sqrt 2 - \sqrt {x - 2} \) \( \Rightarrow A = \sqrt {x - 2} + \sqrt 2 + \sqrt 2 - \sqrt {x - 2} = 2\sqrt 2 .\) Vậy \(A = \left\{ \begin{array}{l}2\sqrt {x - 2} \,\,\,khi\,\,\,x \ge 4\\2\sqrt 2 \,\,\,khi\,\,\,2 \le x < 4\end{array} \right..\) Chọn A. Câu hỏi 34 : Rút gọn biểu thức \(M = \frac{1}{2}\sqrt 5 - 3\sqrt {20} + \frac{1}{3}\sqrt {45} .\)
Đáp án: B Phương pháp giải: Áp dụng phép đưa thừa số ra ngoài dấu căn: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}M = \frac{1}{2}\sqrt 5 - 3\sqrt {20} + \frac{1}{3}\sqrt {45} \\ = \frac{1}{2}\sqrt 5 - 3\sqrt {4.5} + \frac{1}{3}\sqrt {9.5} \\ = \frac{1}{2}\sqrt 5 - 3.2\sqrt 5 + \frac{1}{3}.3.\sqrt 5 \\ = \frac{1}{2}\sqrt 5 - 6\sqrt 5 + \sqrt 5 \\ = \left( {\frac{1}{2} - 6 + 1} \right)\sqrt 5 \\ = - \frac{{9\sqrt 5 }}{2}.\end{array}\) Chọn B. Câu hỏi 35 : Rút gọn biểu thức \(N = \frac{3}{5}\sqrt {12} + \frac{4}{3}\sqrt {27} - \frac{4}{{15}}\sqrt {300} .\)
Đáp án: A Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}N = \frac{3}{5}\sqrt {12} + \frac{4}{3}\sqrt {27} - \frac{4}{{15}}\sqrt {300} \\ = \frac{3}{5}\sqrt {4.3} + \frac{4}{3}\sqrt {9.3} - \frac{4}{{15}}\sqrt {100.3} \\ = \frac{3}{5}.2\sqrt 3 + \frac{4}{3}.3\sqrt 3 - \frac{4}{{15}}.10\sqrt 3 \\ = \frac{6}{5}\sqrt 3 + 4\sqrt 3 - \frac{8}{3}\sqrt 3 \\ = \left( {\frac{6}{5} + 4 - \frac{8}{3}} \right)\sqrt 3 \\ = \frac{{38\sqrt 3 }}{{15}}.\end{array}\) Chọn A. Câu hỏi 36 : Rút gọn \(P = 3\sqrt {8x} - 5\sqrt {48x} + 9\sqrt {18x} + 5\sqrt {12x} \) với \(x > 0\)
Đáp án: C Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}P = 3\sqrt {8x} - 5\sqrt {48x} + 9\sqrt {18x} + 5\sqrt {12x} \\ = 3\sqrt {4.2.x} - 5\sqrt {16.3.x} + 9\sqrt {9.2.x} + 5\sqrt {4.3.x} \\ = 3.2\sqrt {2x} - 5.4\sqrt {3x} + 9.3\sqrt {2x} + 5.2\sqrt {3x} \\ = 6\sqrt {2x} - 20\sqrt {3x} + 27\sqrt {2x} + 10\sqrt {3x} \\ = 33\sqrt {2x} - 10\sqrt {3x} .\end{array}\) Chọn C. Câu hỏi 37 : Rút gọn \(\frac{{\left( {x\sqrt y + y\sqrt x } \right)\left( {\sqrt x - \sqrt y } \right)}}{{\sqrt {xy} }}\) với \(x > 0,\,y > 0.\)
Đáp án: A Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Áp dụng hằng đẳng thức đáng nhớ: \({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) Phân tích biểu thức ở trong căn thành nhân tử. Lời giải chi tiết: \(\begin{array}{l}\frac{{\left( {x\sqrt y + y\sqrt x } \right)\left( {\sqrt x - \sqrt y } \right)}}{{\sqrt {xy} }}\\ = \frac{{\left( {\sqrt x .\sqrt x .\sqrt y + \sqrt y .\sqrt y .\sqrt x } \right)\left( {\sqrt x - \sqrt y } \right)}}{{\sqrt {xy} }}\\ = \frac{{\sqrt {xy} \left( {\sqrt x + \sqrt y } \right)\left( {\sqrt x - \sqrt y } \right)}}{{\sqrt {xy} }}\\ = \left( {\sqrt x + \sqrt y } \right)\left( {\sqrt x - \sqrt y } \right)\\ = {\left( {\sqrt x } \right)^2} - {\left( {\sqrt y } \right)^2}\\ = x - y.\end{array}\) Chọn A. Câu hỏi 38 : Giá trị của \(x\) thỏa mãn phương trình \(\sqrt {{x^2} - 9} - 3\sqrt {x - 3} = 0\) với \(x \ge 3\) là
Đáp án: A Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Áp dụng hằng đẳng thức đáng nhớ: \({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) Phân tích biểu thức ở trong căn thành nhân tử. Giải phương trình : \(\sqrt {f\left( x \right)} = a\,\,\,\left( {a \ge 0} \right) \Leftrightarrow f\left( x \right) = {a^2}.\) Lời giải chi tiết: Điều kiện : \(x \ge 3.\) \(\begin{array}{l}\sqrt {{x^2} - 9} - 3\sqrt {x - 3} = 0\\ \Leftrightarrow \sqrt {\left( {x - 3} \right)\left( {x + 3} \right)} - 3\sqrt {x - 3} = 0\\ \Leftrightarrow \sqrt {x - 3} \left( {\sqrt {x + 3} - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt {x - 3} = 0\\\sqrt {x + 3} - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x - 3 = 0\\\sqrt {x + 3} = 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 3\\x + 3 = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 3\,\,\,\,\,\left( {tm} \right)\\x = 6\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Chọn A. Câu hỏi 39 : Giá trị của \(x\) thỏa mãn phương trình \(\sqrt {{x^2} - 4} - 2\sqrt {x + 2} = 0\) là:
Đáp án: B Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Áp dụng hằng đẳng thức đáng nhớ: \({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) Biến đổi các biểu thức dưới dấu căn về bình phương của một hiệu sau đó áp dụng công thức để đưa biểu thức ra ngoài dấu căn. Áp dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,A < 0\end{array} \right..\) Giải phương trình : \(\sqrt {f\left( x \right)} = a\,\,\,\left( {a \ge 0} \right) \Leftrightarrow f\left( x \right) = {a^2}.\)
Lời giải chi tiết: Điều kiện: \(\left\{ \begin{array}{l}{x^2} - 4 \ge 0\\x + 2 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x \ge 2\\x \le - 2\end{array} \right.\\x \ge - 2\end{array} \right. \Leftrightarrow x \ge 2.\) \(\begin{array}{l}\sqrt {{x^2} - 4} - 2\sqrt {x + 2} = 0\\ \Leftrightarrow \sqrt {\left( {x - 2} \right)\left( {x + 2} \right)} - 2\sqrt {x + 2} = 0\\ \Leftrightarrow \sqrt {x + 2} \left( {\sqrt {x - 2} - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt {x + 2} = 0\\\sqrt {x - 2} - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x + 2 = 0\\\sqrt {x - 2} = 2\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x - 2 = 4\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 2\,\,\,\left( {ktm} \right)\\x = 6\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\) Chọn B. Câu hỏi 40 : Rút gọn biểu thức \(A = \frac{{x - 2}}{{\sqrt {{x^2} - 4x + 4} }}\) với \(x \ne 2\) ta được:
Đáp án: C Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Áp dụng hằng đẳng thức đáng nhớ: \({A^2} - {B^2} = \left( {A + B} \right)\left( {A - B} \right)\) Áp dụng hằng đẳng thức đáng nhớ để xử lý bài toán: \({(A \pm B)^2} = {A^2} \pm 2AB + {B^2}\) Lời giải chi tiết: Điều kiện : \( x \ne 2\) Ta có: \(A = \frac{{x - 2}}{{\sqrt {{x^2} - 4x + 4} }} = \frac{{x - 2}}{{\sqrt {{{\left( {x - 2} \right)}^2}} }} = \frac{{x - 2}}{{\left| {x - 2} \right|}}\) + Nếu \(x < 2\) thì \(\left| {x - 2} \right| = - \left( {x - 2} \right),\) ta có:\(A = \frac{{x - 2}}{{\sqrt {{x^2} - 4x + 4} }}\)\( = \frac{{x - 2}}{{ - \left( {x - 2} \right)}} = - 1\) + Nếu \(x > 2\) thì \(\left| {x - 2} \right| = x - 2,\) ta có:\(A = \frac{{x - 2}}{{\sqrt {{x^2} - 4x + 4} }} = \frac{{x - 2}}{{x - 2}} = 1\) Chọn C.
|