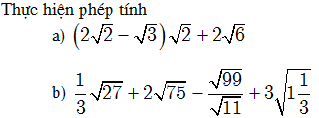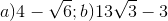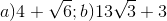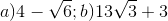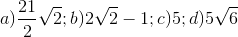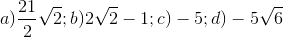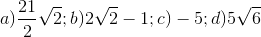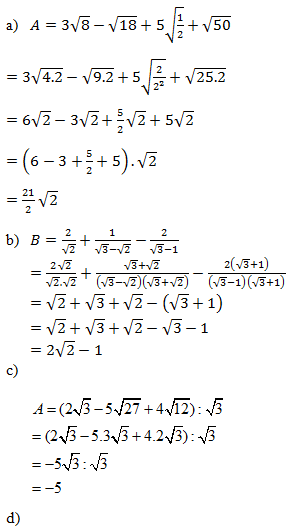20 bài tập cơ bản Biến đổi đơn giản biểu thức chứa căn thức bậc haiLàm bàiCâu hỏi 1 : Khi \(x = 7\) biểu thức \(\frac{4}{{\sqrt {x + 2} - 1}}\) có giá trị là:
Đáp án: D Phương pháp giải: Thay \(x = 7\,\,\,\left( {tm} \right)\)vào biểu thức \(\frac{4}{{\sqrt {x + 2} - 1}}\) ta tính được giá trị của biểu thức tại \(x = 7\). Lời giải chi tiết: Điều kiện: \(\left\{ \begin{array}{l}x + 2 \ge 0\\\sqrt {x + 2} - 1 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x \ne - 1\end{array} \right..\) Thay \(x = 7\,\,\left( {tm} \right)\) vào biểu thức \(\frac{4}{{\sqrt {x + 2} - 1}}\) ta được: \(\frac{4}{{\sqrt {7 + 2} - 1}} = \frac{4}{{3 - 1}} = 2\) Chọn D. Câu hỏi 2 : Đưa thừa số \(x\sqrt {\frac{{ - 29}}{x}} \) vào trong dấu căn với \(x < 0\)
Đáp án: A Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: Với \(x < 0\) ta có : \(x\sqrt {\frac{{ - 29}}{x}} = - \sqrt {{x^2}.\frac{{ - 29}}{x}} = - \sqrt { - 29x} \) Chọn A. Câu hỏi 3 : Đưa thừa số \(\sqrt {25{x^3}} \) ra ngoài dấu căn với \(x > 0\)
Đáp án: B Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: Với \(x > 0\) ta có : \(\sqrt {25{x^3}} = \sqrt {25{x^2}.x} = \left| {5x} \right|\sqrt x = 5x\sqrt x .\) Chọn B. Câu hỏi 5 : Rút gọn biểu thức \(\sqrt {7 - 4\sqrt 3 } + \sqrt 3 \) ta được kết quả là
Đáp án: A Phương pháp giải: - Viết \(7 - 4\sqrt 3 \) dưới dạng bình phương của một hiệu. - Sử dụng định lí: Với mọi số \(a\), ta có \(\sqrt {{a^2}} = \left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}\sqrt {7 - 4\sqrt 3 } + \sqrt 3 \, = \sqrt {4 - 2.2.\sqrt 3 + 3} + \sqrt 3 = \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} + \sqrt 3 \\ = \left| {2 - \sqrt 3 } \right| + \sqrt 3 = 2 - \sqrt 3 + \sqrt 3 = 2\end{array}\) Vậy rút gọn biểu thức \(\sqrt {7 - 4\sqrt 3 } + \sqrt 3 \,\) ta được kết quả là \(2\). Chọn A. Câu hỏi 6 : Rút gọn biểu thức \(P = \frac{{\sqrt {16} + \sqrt {36} }}{{2\sqrt {25} }}\) ta được:
Đáp án: A Phương pháp giải: Sử dụng công thức \(\sqrt {{A^2}} = \left| A \right|\). Lời giải chi tiết: \(P = \frac{{\sqrt {16} + \sqrt {36} }}{{2\sqrt {25} }} = \frac{{4 + 6}}{{2.5}} = \frac{{10}}{{10}} = 1\). Chọn A. Câu hỏi 7 : Biểu thức \(P = \sqrt 5 \left( {\sqrt {10} - \sqrt {40} } \right)\) có giá trị bằng:
Đáp án: D Phương pháp giải: Sử dụng các công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B ;\,\,\,\sqrt {AB} = \sqrt A .\sqrt B .\) Lời giải chi tiết: \(\begin{array}{l}P = \sqrt 5 \left( {\sqrt {10} - \sqrt {40} } \right) = \sqrt 5 \left( {\sqrt {10} - \sqrt {4.10} } \right) = \sqrt 5 \left( {\sqrt {10} - 2\sqrt {10} } \right)\\ = \sqrt 5 .\left( { - \sqrt {10} } \right) = - \sqrt 5 .\sqrt {10} = - \sqrt {5.10} = - \sqrt {50} = - \sqrt {25.2} = - 5\sqrt 2 .\end{array}\) Chọn D. Câu hỏi 8 : Giá trị rút gọn của biểu thức \(P = \sqrt {125} + \sqrt {20} - \sqrt {80} \) bằng:
Đáp án: C Phương pháp giải: Sử dụng các công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,khi\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}P = \sqrt {125} + \sqrt {20} - \sqrt {80} = \sqrt {{5^2}.5} + \sqrt {{2^2}.5} - \sqrt {{4^2}.5} \\\,\,\,\,\, = 5\sqrt 5 + 2\sqrt 5 - 4\sqrt 5 = 3\sqrt 5 .\end{array}\) Chọn C. Câu hỏi 9 : Giá trị của biểu thức \(\frac{{3 + \sqrt 3 }}{{\sqrt 3 + 1}}\) bằng:
Đáp án: B Phương pháp giải: Đặt nhân tử chung ở tử số sau đó rút gọn phân thức hoặc sử dụng phương pháp trục căn thức ở mẫu. Lời giải chi tiết: Ta có: \(\frac{{3 + \sqrt 3 }}{{\sqrt 3 + 1}} = \frac{{\sqrt 3 \left( {\sqrt 3 + 1} \right)}}{{\sqrt 3 + 1}} = \sqrt 3 .\) Chọn B. Câu hỏi 10 : Rút gọn biểu thức \(A = 2\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} + \sqrt {20} - 20\sqrt {\dfrac{1}{5}} \).
Đáp án: A Phương pháp giải: Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\). Lời giải chi tiết: \(A = 2\sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} + \sqrt {20} - 20\sqrt {\dfrac{1}{5}} \) \(\begin{array}{l}A = 2\left| {2 - \sqrt 5 } \right| + \sqrt {4.5} - 4.5.\dfrac{1}{{\sqrt 5 }}\\A = 2\left( {\sqrt 5 - 2} \right) + 2\sqrt 5 - 4\sqrt 5 \,\,\,\,\left( {Do\,\,2 - \sqrt 5 < 0} \right)\\A = 2\sqrt 5 - 4 + 2\sqrt 5 - 4\sqrt 5 \\A = - 4\end{array}\) Vậy \(A = - 4\). Câu hỏi 11 : Đơn giản biểu thức \(\sqrt {75} + \sqrt {48} - \sqrt {300} \) ta được:
Đáp án: C Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}\sqrt {75} + \sqrt {48} - \sqrt {300} \\ = \sqrt {25.3} + \sqrt {16.3} - \sqrt {100.3} \\ = \sqrt {{5^2}.3} + \sqrt {{4^2}.3} - \sqrt {{{10}^2}.3} \\ = 5\sqrt 3 + 4\sqrt 3 - 10\sqrt 3 \\ = \left( {5 + 4 - 10} \right)\sqrt 3 = - \sqrt 3 .\end{array}\) Chọn C. Câu hỏi 12 : Khẳng định nào sau đây là đúng?
Đáp án: D Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: + Đáp án A. \(0,1\sqrt {40000} = 0,1\sqrt {{{200}^2}} \)\( = 0,1.200 = 20\)\( \Rightarrow \) A đúng + Đáp án B. \( - 0,005\sqrt {62500} = - 0,005\sqrt {{{250}^2}} \)\( = - 0.005.250 = - 1,25\)\( \Rightarrow \) B đúng + Đáp án C. \(\sqrt {98} - \sqrt {72} + 0,5\sqrt 8 \) \( = \sqrt {49.2} - \sqrt {36.2} + 0,5\sqrt {4.2} \) \( = \sqrt {{7^2}.2} - \sqrt {{6^2}.2} + 0,5\sqrt {{2^2}.2} \) \( = 7\sqrt 2 - 6\sqrt 2 + 0,5.2\sqrt 2 \) \(\begin{array}{l} = \left( {7 - 6 + 0,5.2} \right)\sqrt 2 \\ = \left( {7 - 6 + 1} \right)\sqrt 2 \\ = 2\sqrt 2 \end{array}\) \( \Rightarrow \) C đúng. Chọn D. Câu hỏi 13 : Biểu thức \(2\sqrt {40\sqrt {12} } - 2\sqrt {\sqrt {75} } - 3\sqrt {5\sqrt {48} } \) sau khi rút gọn là:
Đáp án: B Phương pháp giải: Với \(B \ge 0\), ta có \(\sqrt {{A^2}.B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right..\) Sử dụng công thức hằng đẳng thức : \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}\,\,\,\,\,2\sqrt {40\sqrt {12} } - 2\sqrt {\sqrt {75} } - 3\sqrt {5\sqrt {48} } \\ = 2\sqrt {40\sqrt {4.3} } - 2\sqrt {\sqrt {25.3} } - 3\sqrt {5\sqrt {16.3} } \\ = 2\sqrt {40.2\sqrt 3 } - 2\sqrt {5\sqrt 3 } - 3\sqrt {5.4\sqrt 3 } \\ = 2\sqrt {80} .\sqrt {\sqrt 3 } - 2\sqrt 5 .\sqrt {\sqrt 3 } - 3\sqrt {20} .\sqrt {\sqrt 3 } \\ = 2\sqrt {16.5} \sqrt {\sqrt 3 } - 2\sqrt 5 .\sqrt {\sqrt 3 } - 3\sqrt {4.5} .\sqrt {\sqrt 3 } \\ = 2.4\sqrt 5 .\sqrt {\sqrt 3 } - 2\sqrt 5 .\sqrt {\sqrt 3 } - 3.2\sqrt 5 .\sqrt {\sqrt 3 } \\ = \left( {2.4 - 2 - 3.2} \right)\sqrt 5 .\sqrt {\sqrt 3 } \\ = 0.\sqrt 5 .\sqrt {\sqrt 3 } = 0.\end{array}\) Chọn B. Câu hỏi 14 : Đưa thừa số vào trong dấu căn \(\begin{array}{l}a)\,\,\frac{1}{{xy}}\sqrt {\frac{{{x^2}{y^2}}}{2}} & & & b)\,\,a\sqrt 2 & & & c)\,\, - \frac{a}{b}\sqrt {\frac{b}{a}} \,\,\,\left( {a > 0,\,\,\,b > 0} \right)\\d)\,\,a\sqrt {\frac{3}{a}} & & & e)\,\,\frac{1}{{2x - 1}}\sqrt {5\left( {1 - 4x + 4{x^2}} \right)} .\end{array}\)
Đáp án: B Phương pháp giải: Lời giải chi tiết: \(\begin{array}{l}a)\,\,\frac{1}{{xy}}\sqrt {\frac{{{x^2}{y^2}}}{2}} = \left\{ \begin{array}{l}\frac{{\sqrt 2 }}{2}.\sqrt {\frac{{{x^2}{y^2}}}{{{x^2}{y^2}}}} \,\,\,khi\,\,\,xy > 0\\ - \frac{{\sqrt 2 }}{2}.\sqrt {\frac{{{x^2}{y^2}}}{{{x^2}{y^2}}}} \,\,\,khi\,\,\,xy < 0\end{array} \right. = \left\{ \begin{array}{l}\frac{{\sqrt 2 }}{2}\,\,\,khi\,\,\,xy > 0\\ - \frac{{\sqrt 2 }}{2}\,\,\,khi\,\,\,xy < 0\end{array} \right..\\b)\,\,\,a\sqrt 2 = \left\{ \begin{array}{l}\sqrt {2{a^2}} \,\,\,\,khi\,\,\,a \ge 0\\ - \sqrt {2{a^2}} \,\,\,\,khi\,\,\,a < 0\end{array} \right..\\c)\,\, - \frac{a}{b}\sqrt {\frac{b}{a}} \,\,\,\,\left( {a > 0,\,\,b > 0} \right)\end{array}\) Ta có: \(a > 0;\,\,b > 0 \Rightarrow \frac{a}{b} > 0\) \( \Rightarrow - \frac{a}{b}\sqrt {\frac{b}{a}} = - \sqrt {{{\left( {\frac{a}{b}} \right)}^2}\frac{b}{a}} = - \sqrt {\frac{a}{b}} .\) \(d)\,\,a\sqrt {\frac{3}{a}} \) Điều kiện: \(a > 0.\) Ta có: \(a\sqrt {\frac{3}{a}} = \sqrt {{a^2}.\frac{3}{a}} = \sqrt {3a} .\) \(e)\,\,\frac{1}{{2x - 1}}\sqrt {5\left( {1 - 4x + 4{x^2}} \right)} = \left\{ \begin{array}{l} Câu hỏi 16 :
Đáp án: B Phương pháp giải: Lời giải chi tiết:
Câu hỏi 17 : Phân tích các đa thức sau thành nhân tử: \( \eqalign{& a)\,\,2x - 7\sqrt x - 9\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,d)\,\,3x + 2\sqrt x - 5 \cr & b)\,\,x - 9\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,e)\,\,\,4\sqrt x - x - 4 \cr & c)\,\,x\sqrt x - 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,f)\,\,x + \sqrt x - 6 \cr} \) Phương pháp giải: Lời giải chi tiết: \(\eqalign{& a)\,\,2x - 7\sqrt x - 9 = 2x + 2\sqrt x - 9\sqrt x - 9 \cr & = 2\sqrt x \left( {\sqrt x + 1} \right) - 9\left( {\sqrt x + 1} \right) \cr & = \left( {\sqrt x + 1} \right)\left( {2\sqrt x - 9} \right). \cr & b)\,x - 9 = {\left( {\sqrt x } \right)^2} - {3^2} \cr & = \left( {\sqrt x - 3} \right)\left( {\sqrt x + 3} \right). \cr & c)\,\,x\sqrt x - 1 = {\left( {\sqrt x } \right)^3} - 1 \cr & = \left( {\sqrt x - 1} \right)\left( {x + \sqrt x + 1} \right). \cr & \cr} \) \( \eqalign{& d)\,3x + 2\sqrt x - 5 = 3x - 3\sqrt x + 5\sqrt x - 5 \cr & = 3\sqrt x \left( {\sqrt x - 1} \right) + 5\left( {\sqrt x - 1} \right) \cr & = \left( {\sqrt x - 1} \right)\left( {3\sqrt x + 5} \right). \cr & e)\,4\sqrt x - x - 4 = - \left( {x - 4\sqrt x + 4} \right) \cr & = - {\left( {\sqrt x - 2} \right)^2}. \cr & f)\,x + \sqrt x - 6 = x + 3\sqrt x - 2\sqrt x - 6 \cr & = \sqrt x \left( {\sqrt x + 3} \right) - 2\left( {\sqrt x + 3} \right) \cr & = \left( {\sqrt x + 3} \right)\left( {\sqrt x - 2} \right). \cr} \) Câu hỏi 18 : Tính: a) \(\sqrt{18}-\frac{1}{2}\sqrt{48}-\sqrt{8}+\frac{4-5\sqrt{2}}{5-2\sqrt{2}}\) b) \(\sqrt{{{(2-\sqrt{7})}^{2}}}-\sqrt{\frac{2}{8-3\sqrt{7}}}\) c) \(\frac{\sqrt{8-4\sqrt{3}}}{\sqrt{\sqrt{6}-\sqrt{2}}}.\sqrt{\sqrt{6}+\sqrt{2}}\) Phương pháp giải: Phương pháp: +) Câu a: Khai căn thức bậc hai dựa vào công thức: \(\sqrt{{{A}^{2}}.B}=\left| A \right|\sqrt{B}.\) Sau đó rút gọn biểu thức bằng cách thực hiện các phép tính. +) Câu b: Bỏ căn bậc hai bằng công thức: \(\sqrt{{{A}^{2}}}=\left| A \right|=\left\{ \begin{align} & A\,\,\,\,khi\,\,\,\,A\ge 0 \\ & -A\,\,\,\,khi\,\,\,A<0 \\\end{align} \right..\) Và bỏ căn thức ở mẫu bằng cách trục căn thức ở mẫu: \(\frac{C}{A-\sqrt{B}}=\frac{C\left( A+\sqrt{B} \right)}{{{A}^{2}}-B}.\) Lời giải chi tiết: Giải:
a) \(\begin{array}{l}\,\,\,\,\sqrt {18} - \frac{1}{2}\sqrt {48} - \sqrt 8 + \frac{{4 - 5\sqrt 2 }}{{5 - 2\sqrt 2 }}\\ = 3\sqrt 2 - \frac{1}{2}.4\sqrt 3 - 2\sqrt 2 + \frac{{\sqrt 2 \left( {2\sqrt 2 - 5} \right)}}{{5 - 2\sqrt 2 }}\\ = \sqrt 2 - 2\sqrt 3 - \sqrt 2 = - 2\sqrt 3 .\end{array}\) b) \(\begin{array}{l}\,\,\,\sqrt {{{\left( {2 - \sqrt 7 } \right)}^2}} - \sqrt {\frac{1}{{8 - 3\sqrt 7 }}} = \left| {2 - \sqrt 7 } \right| - \sqrt {\frac{{{{\left( {3 + \sqrt 7 } \right)}^2}}}{{64 - 63}}} \\ = \sqrt 7 - 2 - \left| {3 + \sqrt 7 } \right| = \sqrt 7 - 2 - 3 - \sqrt 7 = - 5.\end{array}\) c) \(\begin{array}{l}\,\,\,\,\frac{{\sqrt {8 - 4\sqrt 3 } }}{{\sqrt {\sqrt 6 - \sqrt 2 } }}.\sqrt {\sqrt 6 + \sqrt 2 } = \frac{{\sqrt {6 - 2.\sqrt 6 .\sqrt 2 + } 2}}{{\sqrt {\sqrt 6 - \sqrt 2 } }}.\sqrt {\sqrt 6 + \sqrt 2 } \\ = \sqrt {\frac{{{{\left( {\sqrt 6 - \sqrt 2 } \right)}^2}}}{{\sqrt 6 - \sqrt 2 }}} .\sqrt {\sqrt 6 + \sqrt 2 } = \sqrt {\left( {\sqrt 6 - \sqrt 2 } \right)\left( {\sqrt 6 + \sqrt 2 } \right)} \\ = \sqrt {6 - 2} = \sqrt 4 = 2.\end{array}\) Câu hỏi 19 : Tính giá trị của các biểu thức: \(a)\;A = 5\sqrt {27} - 5\sqrt 3 - 2\sqrt {12} \) \(b)\;B = \frac{{\sqrt {15} - \sqrt 3 }}{{\sqrt 5 - 1}} - \frac{{\sqrt {15} + \sqrt 3 }}{{\sqrt 5 + 1}}\)
Đáp án: A Phương pháp giải: +) Sử dụng công thức: \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \;\;\;khi\;\;\;A \ge 0\\ - A\sqrt B \;\;\;khi\;\;\;A < 0\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}a)\;A = 5\sqrt {27} - 5\sqrt 3 - 2\sqrt {12} \\\;\;\;\;\;\;\; = 5\sqrt {{3^2}.3} - 5\sqrt 3 - 2\sqrt {{2^2}.3} \\\;\;\;\;\;\;\; = 5.3\sqrt 3 - 5\sqrt 5 - 2.2\sqrt 3 \\\;\;\;\;\;\;\; = 6\sqrt 3 .\end{array}\) \(\begin{array}{l}b)\;B = \frac{{\sqrt {15} - \sqrt 3 }}{{\sqrt 5 - 1}} - \frac{{\sqrt {15} + \sqrt 3 }}{{\sqrt 5 + 1}}\\\;\;\;\;\;\;\; = \frac{{\sqrt 3 \left( {\sqrt 5 - 1} \right)}}{{\sqrt 5 - 1}} - \frac{{\sqrt 3 \left( {\sqrt 5 + 1} \right)}}{{\sqrt 5 + 1}}\\\;\;\;\;\;\;\; = \sqrt 3 - \sqrt 3 = 0.\end{array}\) Chọn A. Câu hỏi 20 : Thực hiện phép tính: 1)\(A = \sqrt {12} - 2\sqrt {48} + \frac{7}{5}\sqrt {75} \) 2)\(B = \sqrt {14 - 6\sqrt 5 } + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \)
Đáp án: A Phương pháp giải: 1) Áp dụng công thức \(\sqrt {{a^2}b} = a\sqrt b \left( {a,b \ge 0} \right)\) 2) Áp dụng công thức \(\sqrt {{a^2}} = \left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;a\; < \;0\end{array} \right..\) Lời giải chi tiết: Thực hiện phép tính: \(\begin{array}{l}1)\;\;A = \sqrt {12} - 2\sqrt {48} + \frac{7}{5}\sqrt {75} \\\;\;\; = \sqrt {{2^2}.3} - 2\sqrt {{4^2}.3} + \frac{7}{5}\sqrt {{5^2}.3} \\\;\;\; = 2\sqrt 3 - 2.4\sqrt 3 + \frac{7}{5}.5\sqrt 3 = \sqrt 3 .\end{array}\) Vậy \(A = \sqrt 3 \).\(\) \(\begin{array}{l}2)\;\;B = \sqrt {14 - 6\sqrt 5 } + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \sqrt {{3^2} + 2.3.\sqrt 5 + {{\left( {\sqrt 5 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \sqrt {{{\left( {3 + \sqrt 5 } \right)}^2}} + \sqrt {{{\left( {2 - \sqrt 5 } \right)}^2}} \\\;\;\;\;\;\;\; = \left| {3 + \sqrt 5 } \right| + \left| {2 - \sqrt 5 } \right|\\\;\;\;\;\;\;\; = 3 + \sqrt 5 + \sqrt 5 - 2\; = 2\sqrt {5 + 1} .\;\;\;\left( {do\;\;\;\sqrt 5 - 2 > 0} \right)\end{array}\) Vậy \(B = 2\sqrt 5 + 1\) Chọn A.
|