40 bài tập trắc nghiệm sự đồng biến nghịch biến của hàm số mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Tìm tất cả các giá trị thực của tham số m để hàm số y=x+m(sinx+cosx) đồng biến trên R.
Đáp án: B Phương pháp giải: - Hàm số y=f(x) đồng biến trên (a;b)⇔f′(x)≥0∀x∈(a;b). Lời giải chi tiết: Ta có: y′=1+m(cosx−sinx)=1+√2mcos(x+π4). Hàm số đồng biến trên R ⇔y′≥0 với ∀x∈R . Vì −1≤cos(x+π4)≤1⇒y′≥0⇔{1−√2m≥01+√2m≥0⇔{m≤√22m≥−√22⇔−√22≤m≤√22. Chọn B. Câu hỏi 2 : Xác định giá trị của m để hàm số y=x3+3x2+mx+mnghịch biến trên một khoảng có độ dài bằng 1.
Đáp án: A Phương pháp giải: Hàm số nghịch biến trên đoạn có độ dài bằng 1⇔ hàm số có y′<0 và phương trình y′=0 có hai nghiệm x1,x2 sao cho |x1−x2|=1. Lời giải chi tiết: Ta có: y′=3x2+6x+m Hàm số nghịch biến trên một khoảng có độ dài bằng 1 thì pt y′=0 phải có hai nghiệm phân biệt x1;x2 và |x1−x2|=1⇔{Δ′>0|x1−x2|=1⇔{9−3m>0(x1+x2)2−4x1x2=1(*). Theo hệ thức Vi-ét ta có: {x1+x2=−2x1x2=m3 ⇒(∗)⇔{m<34−43m=1⇔{m<3m=94⇔m=94. Chọn A. Câu hỏi 3 : Tìm tham số m để hàm số y=−x33+(m−2)x2−m(m−3)x−13 nghịch biến trên khoảng (1;+∞).
Đáp án: B Phương pháp giải: Lời giải chi tiết: Giải: Ta có:y′=−x2+2(m−2)x−m2+3m . Để hàm số nghịch biến trên (1;+∞) thì y′≤0∀x∈(1;+∞) . Để giải nhanh bài toán này, ta nên dùng máy tính để thử các đáp án. Trước hết ta thử với m=4 . +) Với m=4 suy ra y′=−x2+4x−4=−(x−2)2≤0∀x∈(1;+∞) hàm số nghịch biến ⇒ loại đáp án A và D. Ta thấy 5−√52<4 cách viết của đáp án C sai. Chọn B. Câu hỏi 4 : Xác định giá trị của m để hàm số f(x)=−13x3+(m−1)x2+(m+3)x đồng biến trên khoảng (0; 3).
Đáp án: A Phương pháp giải: - Hàm số đồng biến trên (0;3)⇔y′≥0∀x∈(0;3). Lời giải chi tiết: Để hàm số đồng biến trên (0;3) thì y′=−x2+2(m−1)x+m+3≥0∀x∈(0;3) ⇒m(2x+1)≥x2+2x−3∀x∈(0;3)⇔m≥x2+2x−32x+1=f(x)∀x∈(0;3)(Do2x+1>0∀x∈(0;3))⇒m≥max Ta có: \begin{array}{l} f'\left( x \right) = \dfrac{{\left( {2x + 2} \right)\left( {2x + 1} \right) - 2\left( {{x^2} + 2x - 3} \right)}}{{{{\left( {2x + 1} \right)}^2}}}\\ f'\left( x \right) = \dfrac{{4{x^2} + 6x + 2 - 2{x^2} - 4x + 6}}{{{{\left( {2x + 1} \right)}^2}}}\\ f'\left( x \right) = \dfrac{{2{x^2} + 2x + 8}}{{{{\left( {2x + 1} \right)}^2}}} > 0\,\,\forall x \in \left[ {0;3} \right]\\ \Rightarrow \mathop {\max }\limits_{\left[ {0;3} \right]} f\left( x \right) = f\left( 3 \right) = \dfrac{{12}}{7}\\ \Rightarrow m \ge \dfrac{{12}}{7} \end{array} Chọn A. Câu hỏi 5 : Xác định giá trị của m để hàm số y=\dfrac{mx+3}{3x+m} nghịch biến trên từng khoảng xác định của nó.
Đáp án: D Phương pháp giải: - Hàm số y=\dfrac{ax+b}{cx+d}\,\,\left( ad-bc\ne 0 \right) đơn điệu trên từng khoảng xác định khi và chỉ khi y' < 0 với mọi x thuộc tập xác định. Lời giải chi tiết: Đk: x \ne - \dfrac{m}{3}. Ta có: y' = \dfrac{{{m^2} - 9}}{{{{\left( {3x + m} \right)}^2}}}. Để hàm số nghịch biến trên từng khoảng xác định của nó thì hàm số phải xác định và y'<0\,\,\forall x\ne -\dfrac{m}{3}. \Leftrightarrow {m^2} - 9 < 0 \Leftrightarrow - 3 < m < 3 Chọn D. Câu hỏi 6 : Hàm số y = \dfrac{{x + 2}}{{x - m}} đồng biến trên \left( 2;+\infty \right) khi:
Đáp án: D Phương pháp giải: - Hàm số đồng biến trên \left( {2; + \infty } \right) \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {2; + \infty } \right) và xác định trên \left( {2; + \infty } \right). Lời giải chi tiết: Đk: x \ne m. Ta có: y' = \dfrac{{ - m - 2}}{{{{\left( {x - m} \right)}^2}}}. Để hàm số đồng biến trên \left( {2; + \infty } \right) thì y' > 0\,\forall x \in \left( {2; + \infty } \right) và hàm số xác định trên \left( {2; + \infty } \right). \Rightarrow y' > 0 \Leftrightarrow - m - 2 > 0 \Leftrightarrow m < - 2 Ta thấy m < - 2 thì hàm số xác định với \forall x \in \left( {0;2} \right). Chọn D. Câu hỏi 7 : Xác định giá trị của m để hàm số y = \sqrt {{x^2} + 2mx + {m^2} + 3} đồng biến trên khoảng \left( {2; + \infty } \right).
Đáp án: B Phương pháp giải: - Hàm số đồng biến trên \left( {2; + \infty } \right) \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {2; + \infty } \right). Lời giải chi tiết: Đk: {x^2} + 2mx + {m^2} + 3 \ge 0 \Leftrightarrow \Delta ' \le 0 \Leftrightarrow {m^2} - {m^2} - 3 \le 0\,\forall m \Rightarrow hàm số luôn xác định với mọi m. Ta có: y' = \dfrac{{x + m}}{{\sqrt {{x^2} + 2mx + {m^2} + 3} }} Hàm số đồng biến trên khoảng \left( {2; + \infty } \right) thì y' \ge 0 với mọi x \in \left( {2; + \infty } \right) \Leftrightarrow - m \le 2 \Leftrightarrow m \ge - 2 Chọn B. Câu hỏi 8 : Cho hàm sốy = - \dfrac{1}{3}{x^3} + m{x^2} + \left( {m - 2} \right)x - \dfrac{1}{3}. Tìm các giá trị của m để hàm số đã cho đồng biến trên đoạn có độ dài bằng 4.
Đáp án: C Phương pháp giải: - Hàm số đồng biến trên đoạn có độ dài bằng 4 \Leftrightarrow Hàm số có y' > 0 và phương trình y' = 0 có 2 nghiệm phân biệt {{x}_{1}},\,\,{{x}_{2}} thỏa mãn \left| {{x}_{1}}-{{x}_{2}} \right|=4. Lời giải chi tiết: Ta có: y' = - {x^2} + 2mx + m - 2 có \Delta ' = {m^2} + m - 2. Hàm số đồng biến trên đoạn có độ dài bằng 4 \Leftrightarrow y'=0 có hai nghiệm phân biệt {x_1};\,{x_2} sao cho |{x_1} - {x_2}| = 4 \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\|{x_1} - {x_2}| = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 2 > 0\\{\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 16\end{array} \right.(*). Theo định lý Vi-ét ta có: \left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1}{x_2} = - m + 2\end{array} \right. \Rightarrow \left( * \right) \Leftrightarrow \left\{ \begin{array}{l}{m^2} + m - 2 > 0\\4{m^2} + 4\left( {m - 2} \right) = 16\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m < - 2\\m > 1\end{array} \right.\\{m^2} + m - 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m < - 2\\m > 1\end{array} \right.\\\left[ \begin{array}{l}m = 2\\m = - 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 2\\m = - 3\end{array} \right. Chọn C. Câu hỏi 9 : Tìm tất cả các giá trị thực của m sao cho hàm số y = \dfrac{{\tan x - 2}}{{m\tan x - 2}} đồng biến trên khoảng \left( {0;\dfrac{\pi }{4}} \right).
Đáp án: D Phương pháp giải: - Hàm số đồng biến trên \left( {0;\dfrac{\pi }{4}} \right) \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {0;\dfrac{\pi }{4}} \right). Lời giải chi tiết: Ta có: y' = \dfrac{{\left( {m\tan x - 2} \right).\dfrac{1}{{{{\cos }^2}x}} - \left( {\tan x - 2} \right).m.\dfrac{1}{{{{\cos }^2}x}}}}{{{{\left( {m\tan x - 2} \right)}^2}}} = \dfrac{{2\left( {m - 1} \right)}}{{{{\cos }^2}x{{\left( {m\tan x - 2} \right)}^2}}}. Hàm số đồng biến trên khoảng \left( {0;\dfrac{\pi }{4}} \right) thì hàm số phải xác định trên \left( {0;\dfrac{\pi }{4}} \right) và y' \ge 0 với \forall x \in \left( {0;\dfrac{\pi }{4}} \right). TH1: m = 0 \Rightarrow y = - \dfrac{1}{2}\left( {\tan x - 2} \right) là hàm nghịch biến trên \left( {0;\dfrac{\pi }{4}} \right) \Rightarrow loại m = 0. TH2: m \ne 0 ta có: y = \dfrac{{\tan x - 2}}{{m\tan x - 2}} = \dfrac{{\tan x - 2}}{{m\left( {\tan x - \dfrac{2}{m}} \right)}}..hàm số xác định với \forall x \in \left( {0;\dfrac{\pi }{4}} \right) thì \dfrac{2}{m} \notin \left( {0;1} \right) vì khi x \in \left( {0;\dfrac{\pi }{4}} \right) thì \tan x \in \left( {0;1} \right) \Rightarrow \left[ \begin{array}{l}\dfrac{2}{m} \le 0\\\dfrac{2}{m} \ge 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 0\\0 < m \le 2\end{array} \right.. Ta có: y' > 0 \Leftrightarrow m - 1 > 0 \Leftrightarrow m > 1. Kết hợp với điều kiện ta có hàm số đồng biến trên \left( {0;\dfrac{\pi }{4}} \right) khi 1 < m \le 2. Chọn D. Câu hỏi 10 : Cho hàm số y = f\left( x \right) = \dfrac{{2{x^2} - mx + m + 2}}{{ - x + m + 1}}. Để hàm số nghịch biến trong \left( {2; + \infty } \right), giá trị cần tìm của tham số m là:
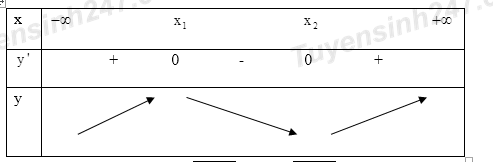
Đáp án: B Phương pháp giải: - Hàm số nghịch biến trên \left( {2; + \infty } \right) \Leftrightarrow y' \le 0\,\,\forall x \in \left( {2; + \infty } \right). Lời giải chi tiết: Ta có: y' = \dfrac{{ - 2{x^2} + 4\left( {m + 1} \right)x - {m^2} + 2}}{{{{\left( { - x + m + 1} \right)}^2}}} Để hàm số nghịch biến trên \left( {2; + \infty } \right) \Rightarrow y' \le 0\,\,\forall x \in \left( {2; + \infty } \right). \Rightarrow g\left( x \right) = - 2{x^2} + 4\left( {m + 1} \right)x - {m^2} + 2 \le 0\,\,\forall x \in \left( {2; + \infty } \right). Ta có: \Delta ' = 4\left( {{m^2} + 2m + 1} \right) - 2{m^2} + 4 = 2{\left( {m + 2} \right)^2} \ge 0 với mọi m. Gọi {x_1} \le {x_2} là hai nghiệm của phương trình g\left( x \right) = 0, ta có BXD :
Dựa vào BBT ta thấy : Để g\left( x \right) \le 0\,\,\forall x \in \left( {2; + \infty } \right) thì \left( {2; + \infty } \right) \subset \left( {{x_2}; + \infty } \right) \Rightarrow {x_1} \le {x_2} \le 2. \Rightarrow \left\{ \begin{array}{l}{x_1} + {x_2} \le 4\\\left( {{x_1} - 2} \right)\left( {{x_2} - 2} \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} \le 4\\{x_1}{x_2} - 2\left( {{x_1} + {x_2}} \right) + 4 \ge 0\end{array} \right.. Áp dụng định lí Vi-ét ta có : \left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right)\\{x_1}{x_2} = \dfrac{{{m^2} - 2}}{2}\end{array} \right.. \begin{array}{l} \Rightarrow \left\{ \begin{array}{l}2\left( {m + 1} \right) \le 4\\\dfrac{{{m^2} - 2}}{2} - 4\left( {m + 1} \right) + 4 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m + 1 \le 2\\{m^2} - 2 - 8m - 8 + 8 \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \le 1\\{m^2} - 8m - 2 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \le 1\\\left[ \begin{array}{l}m \ge 4 + 3\sqrt 2 \\m \le 4 - 3\sqrt 2 \end{array} \right.\end{array} \right. \Leftrightarrow m \le 4 - 3\sqrt 2 \end{array} Chọn B. Câu hỏi 11 : Tìm tất cả các giá trị của m để hàm số y=\dfrac{x-1}{x-m} nghịch biến trên khoảng \left( -\infty ;3 \right).
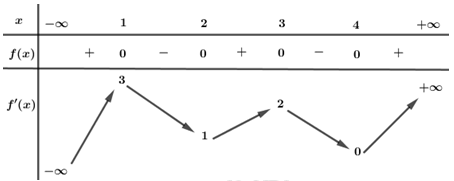
Đáp án: A Phương pháp giải: - Hàm số nghịch biến trên \left( -\infty ;3 \right)\Leftrightarrow y'\le 0\,\,\forall x\in \left( -\infty ;3 \right). Lời giải chi tiết: Khi m=1 thì y = 1 là hàm hằng trên \mathbb{R} nên m = 1 không thỏa mãn. Khi m\ne 1 thì hàm số có y' = \dfrac{{ - m + 1}}{{{{(x - m)}^2}}} Để hàm số nghịch biến trên khoảng \left( { - \infty ;3} \right) thì\left\{ {\begin{array}{*{20}{c}}{x \ne m}\\{ - m + 1 < 0}\end{array}} \right.\,\,\,\,\forall \,x \in \left( { - \infty ;3} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{m \ge 3}\\{m > 1}\end{array}} \right. \Leftrightarrow m \ge 3 Chọn A. Câu hỏi 12 : Cho hàm số f\left( x \right) có tính chất: f'\left( x \right) \ge 0, \forall x \in \left( {0;3} \right) và f'\left( x \right) = 0 \Leftrightarrow x \in \left( {1;2} \right). Chọn khẳng định sai trong các khẳng định sau.
Đáp án: B Phương pháp giải: - Hàm số y = f\left( x \right) có f'\left( x \right)\ge 0 trên \left( a;b \right) và bằng 0 tại hữu hạn điểm \Rightarrow Hàm số đồng biến trên \left( a;b \right). - Hàm số y=f\left( x \right) có f'\left( x \right)\le 0 trên \left( a;b \right) và bằng 0 tại hữu hạn điểm \Rightarrow Hàm số nghịch biến trên \left( a;b \right). - Hàm số y=f\left( x \right) có f'\left( x \right)=0 trên \left( {a;b} \right) \Rightarrow Hàm số không đổi trên \left( a;b \right). Lời giải chi tiết: Theo đề bài ta có: f'\left( x \right) = 0 \Leftrightarrow x \in \left( {1;2} \right) \Rightarrow là hàm hằng trên khoảng \left( 1;2 \right) \Rightarrow C đúng. Lại có f'\left( x \right)\ge 0, \forall x \in \left( {0;3} \right)\Rightarrow hàm số đồng biến trên \left( 0;1 \right) và \left( 2;3 \right) \Rightarrow A và D đúng. Chọn B. Câu hỏi 13 : Tìm m để hàm số y = {x^3} + 3{x^2} + \left( {m + 1} \right)x + 4m nghịch biến trên (-1; 1).
Đáp án: A Phương pháp giải: Cách 1: Thay từng giá trị của m ở các đáp án và khảo sát hàm số để tìm đáp án đúng. Cách 2: Hàm số nghịch biến trên (-1; \, \, 1) \Leftrightarrow y' \ge 0\;\;\forall x \in \left( { - 1;\;1} \right). Lời giải chi tiết: Cách 1: Giải: Ta có: y' = 3{x^2} + 6x + m + 1 Để giải nhanh bài toán này ta nên dùng máy tính để thử từng đáp án. Thử với m = 2 ta có:y' = 3{x^2} + 6x + 3 = 3{\left( {x + 1} \right)^2} \ge 0\,\,\forall x \in R. \Rightarrow với m = 2, hàm số luôn đồng biến \Rightarrow loại đáp án B, C. Còn lại đáp án A và D Thử với m = - 5 ta có: y' = 3{x^2} + 6x - 4. Để hàm số nghịch biến trên (-1; 1) thì y' \le 0\,\,\forall x \in \left( { - 1;1} \right). Nhập hàm y' = 3{x^2} + 6x - 4 vào máy tính và thử với giá trị x = 0,6 ta được y' = 0,68 > 0 nên hàm số đồng biến trong (-1;1). \Rightarrow loại D. Chọn A. Cách 2: Ta có \begin{array}{l}y' = 3{x^2} + 6x + m + 1 \le 0\,\,\forall x \in \left( { - 1;1} \right)\\ \Leftrightarrow m \le - 3{x^2} - 6x - 1\,\,\forall x \in \left( { - 1;1} \right)\\ \Leftrightarrow m \le f\left( x \right)\,\,\forall x \in \left( { - 1;1} \right)\\ \Leftrightarrow m \le \mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( x \right)\end{array} Ta có f'\left( x \right) = - 6x - 6 = 0 \Leftrightarrow x = - 1 f\left( { - 1} \right) = 2;\,\,f\left( 1 \right) = - 10 \Rightarrow \mathop {\min }\limits_{\left[ { - 1;1} \right]} f\left( x \right) = - 10 \Rightarrow m \le - 10 Chọn A. Câu hỏi 14 : Tìm m để hàm số y = {x^3} - 2m{x^2} - \left( {m + 1} \right)x + 1 nghịch biến trên đoạn \left[ {0;2} \right].
Đáp án: C Phương pháp giải: Sử dụng chức năng Mode 7 để thử các đáp án. Lời giải chi tiết: Ta có: y' = 3{x^2} - 4mx - m - 1. Để hàm số nghịch biến trên đoạn \left[ {0;2} \right] thì y' \le 0\,\forall x \in \left[ {0;2} \right]. Ta sử dụng máy tính để thử đáp án với với các giá trị m tương ứng và với giá trị x = 1. +) Trước hết, ta thử với m = \dfrac{{11}}{9} \Rightarrow y' = 3{x^2} - \dfrac{{44}}{9}x - \dfrac{{20}}{9}. Nhập hàm số trên vào máy tính và tính giá trị của hàm số khi x = 1 ta được: y' = - \dfrac{{37}}{9} < 0
\Rightarrow hàm số nghịch biến \Rightarrow m = \dfrac{{11}}{9} thỏa mãn \Rightarrow ta loại đáp án A và B. +) Thử với m = 2 \Rightarrow y' = 3{x^2} - 8x - 3. Nhập hàm số trên vào máy tính và tính giá trị của hàm số khi x = 1 ta được: y' = - 8 < 0
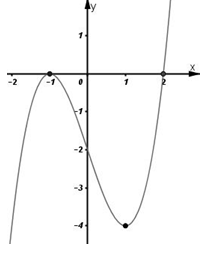
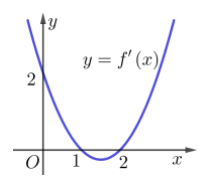
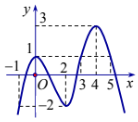
\Rightarrow hàm số nghịch biến \Rightarrow C đúng, D sai. Chọn C. Câu hỏi 15 : Cho hàm số y=f\left( x \right) có đạo hàm trên \mathbb{R}. Đường cong trong hình vẽ bên là đồ thị của hàm số y=f'\left( x \right), (y=f'\left( x \right) liên tục trên \mathbb{R} ). Xét hàm số g\left( x \right)=f\left( {{x}^{2}}-2 \right). Mệnh đề nào dưới đây sai?
Đáp án: C Phương pháp giải: Sử dụng tính chất hàm số g đồng biến ( tương ứng nghịch biến) trên D khi g'\left( x \right)\ge 0,\,\,\forall x\in D (tương ứng g'\left( x \right)\ge 0,\,\,\forall x\in D). Lời giải chi tiết: Quan sát đồ thị hàm số ta thấy f'\left( x \right) < 0 \Leftrightarrow \left\{ \begin{array}{l}x < 2\\x \ne - 1\end{array} \right.,\,\,f'\left( x \right) > 0 \Leftrightarrow x > 2. Ta có g'\left( x \right)=2xf'\left( {{x}^{2}}-2 \right). Hàm số g\left( x \right) đồng biến khi và chỉ khi g'\left( x \right) > 0 \Leftrightarrow xf'\left( {{x^2} - 2} \right) > 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\f'\left( {{x^2} - 2} \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\f'\left( {{x^2} - 2} \right) < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 0\\{x^2} - 2 > 2\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\{x^2} - 2 < 2\\{x^2} - 2 \ne - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > 2\\\left\{ \begin{array}{l} - 2 < x < 0\\x \ne - 1\end{array} \right.\end{array} \right.. Như vậy hàm số đồng biến trên khoảng \left( 2;+\infty \right). Hàm số g\left( x \right) nghịch biến khi và chỉ khi
g'\left( x \right) < 0 \Leftrightarrow xf'\left( {{x^2} - 2} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\f'\left( {{x^2} - 2} \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\f'\left( {{x^2} - 2} \right) < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < 0\\{x^2} - 2 > 2\end{array} \right.\\\left\{ \begin{array}{l}x > 0\\{x^2} - 2 < 2\\{x^2} - 2 \ne - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x < - 2\\0 < x < 2\end{array} \right.. Như vậy hàm số nghịch biến trên \left( -\infty ;-2 \right) và \left( 0;2 \right). Vậy đáp án C sai. Chọn đáp án C. Câu hỏi 16 : Cho hàm số f(x) có đạo hàm trên R và có đồ thị hàm y=f'\left( x \right) như hình vẽ. Xét hàm số g\left( x \right)=f\left( {{x}^{2}}-2 \right). Mệnh đề nào dưới đây sai?
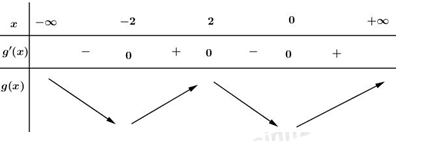
Đáp án: B Phương pháp giải: Dựa vào đồ thị hàm số của hàm y=f'\left( x \right) để xét tính đơn điệu của hàm số y=f\left( x \right) Từ đó ta xét các điểm cực trị của hàm f(x) và suy ra tính đơn điệu của hàm g\left( x \right)=f\left( {{x}^{2}}-2 \right). Lời giải chi tiết: Xét đồ thị hàm số y=f'\left( x \right) ta thấy f'\left( -1 \right)=f'\left( 2 \right)=0. Tuy nhiên tại x=-1 thì f’(x) không đổi dấu nên x=-1 không là điểm cực trị của hàm y=f\left( x \right) Với x>2 thì f'\left( x \right)>0\Rightarrow f\left( x \right) đồng biến trên \left( 2;+\infty \right). Ta có: g\left( x \right)=f\left( {{x}^{2}}-2 \right)\Rightarrow g'\left( x \right)=\left( f\left( {{x}^{2}}-2 \right) \right)'=2x.f'\left( {{x}^{2}}-2 \right). \Rightarrow g'\left( x \right) = 0 \Leftrightarrow 2x.f'\left( {{x^2} - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {{x^2} - 2} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} - 2 = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 2\end{array} \right.. Ta có bảng biến thiên: Dựa vào bảng biến thiên ta thấy B sai.
Chọn B. Câu hỏi 17 : Số các giá trị nguyên của m để hàm số y = \dfrac{{mx - 2}}{{2x - m}} đồng biến trên mỗi khoảng xác định là:
Đáp án: A Phương pháp giải: Hàm số y = f\left( x \right) đồng biến trên mỗi khoảng xác định khi và chỉ khi f'\left( x \right) \ge 0 trên toàn bộ TXĐ và chỉ bằng 0 tại hữu hạn điểm. Lời giải chi tiết: Khi m = 2 hàm số có dạng y = \dfrac{{2x - 2}}{{2x - 2}} = 1 là hàm hằng nên không đồng biến trên mỗi khoảng xác định, loại. Khi m = - 2 hàm số có dạng y = \dfrac{{ - 2x - 2}}{{2x + 2}} = - 1 là hàm hằng nên không đồng biến trên mỗi khoảng xác định, loại. Khi m \ne \pm 2, ĐKXĐ: x \ne \dfrac{m}{2}. Hàm số đồng biến trên mỗi khoảng xác định của nó khi và chỉ khi y' \ge 0 trên TXĐ và chỉ bằng 0 tại hữu hạn điểm. Ta có: y' = \dfrac{{ - {m^2} + 4}}{{{{\left( {2x - m} \right)}^2}}} \ge 0 \Rightarrow - {m^2} + 4 \ge 0 \Leftrightarrow - 2 \le m \le 2. Kết hợp nghiệm ta có - 2 < m < 2, mà m \in Z \Rightarrow m \in \left\{ { - 1;0;1} \right\} \Rightarrow có 3 giá trị của m thỏa mãn yêu cầu bài toán. Chọn A. Câu hỏi 18 : Tìm tất cả các giá trị thực của m để hàm số y = \dfrac{1}{3}{x^3} - 2{x^2} + \left( {m + 5} \right)x + 2m - 5 đồng biến trên khoảng \left( {3; + \infty } \right)
Đáp án: D Phương pháp giải: Áp dụng lý thuyết về tính đồng biến của hàm số
Lời giải chi tiết: Ta có: y = \dfrac{1}{3}{x^3} - 2{x^2} + \left( {m + 5} \right)x + 2m - 5 \Rightarrow y' = {x^2} - 4x + m + 5 với \Delta {'_{y'}} = - m - 1 - Nếu m \ge - 1 \Rightarrow - m - 1 \le 0 \Rightarrow \Delta {'_{y'}} \le 0 \Rightarrow y' \ge 0\forall x Khi đó hàm số đồng biến trên R hay hàm số đồng biến trên khoảng \left( {3; + \infty } \right) - Nếu m < - 1 \Rightarrow - m - 1 > 0 \Rightarrow \Delta {'_{y'}} > 0. Khi đó phương trình y' = 0 có hai nghiệm phân biệt {x_1};{x_2}\left( {{x_1} < {x_2}} \right) Ta có bảng biến thiên của y:
Hàm số đồng biến trên \left( {3; + \infty } \right) \Leftrightarrow {x_2} \le 3 \Leftrightarrow 2 + \sqrt { - m - 1} \le 3 \Leftrightarrow \sqrt { - m - 1} \le 1 \Leftrightarrow 0 \le - m - 1 \le 1 \Leftrightarrow - 2 \le m \le - 1 Kết hợp nghiệm ta có m \in \left[ { - 2; - 1} \right] \cup \left[ { - 1; + \infty } \right) = \left[ { - 2; + \infty } \right) hay m \ge - 2. Chọn D. Câu hỏi 19 : Tìm tất cả những giá trị của m để hàm số y = \dfrac{{\cot 2x + m + 2}}{{\cot 2x - m}} đồng biến trên \left( {\dfrac{\pi }{6};\dfrac{\pi }{4}} \right)
Đáp án: C Phương pháp giải: Áp dụng lý thuyết về tính đồng biến của hàm số Lời giải chi tiết: Đặt \cot 2x = t\left( {t \in R} \right). Khi đó bài toán trở thành tìm m để hàm số y = \dfrac{{t + m + 2}}{{t - m}} nghịch biến trên \left( {0;\dfrac{{\sqrt 3 }}{3}} \right) Ta có: y' = \dfrac{{ - 2m - 2}}{{{{\left( {t - m} \right)}^2}}}. Hàm số nghịch biến trên \left( {0;\dfrac{{\sqrt 3 }}{3}} \right) khi \left\{ {\begin{array}{*{20}{l}}{\dfrac{{ - 2m - 2}}{{{{\left( {t - m} \right)}^2}}} \le 0}\\{m \notin \left( {0;\dfrac{{\sqrt 3 }}{3}} \right)}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ge - 1\\\left[ \begin{array}{l}m \le 0\\m \ge \dfrac{{\sqrt 3 }}{3}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 1 \le m \le 0\\m \ge \dfrac{{\sqrt 3 }}{3}\end{array} \right. Khi m=-1 hàm số trở thành y = \dfrac{{t + 1}}{{t + 1}} = 1 \Rightarrow hàm số ban đầu trở thành hàm hằng nên không thỏa mãn yêu cầu bài toán. Vậy \left[ \begin{array}{l} - 1 < m \le 0\\m \ge \dfrac{{\sqrt 3 }}{3}\end{array} \right.. Chọn C. Câu hỏi 20 : Tìm m để hàm số y = \dfrac{{2\cos x + 1}}{{\cos x - m}} đồng biến trên khoảng \left( {0;\pi } \right).
Đáp án: D Phương pháp giải: Tính đạo hàm y'. Để hàm số đồng biến trên \left( {0;\pi } \right) thì ta cần y'\left( x \right) > 0,\,\,\forall x \in \left( {0;\pi } \right). Giải bất phương trình để tìm m. Lời giải chi tiết: Để hàm số y đồng biến trên \left( {0;\pi } \right) thì trước hết tập xác định của hàm số phải là \left( {0;\pi } \right). Do với x \in \left( {0;\pi } \right) thì \cos x \in \left( { - 1;1} \right) nên điều kiện cần là \left| m \right| \ge 1. Với \left| m \right| \ge 1 ta có y'\left( x \right) = \dfrac{{2m\sin x + {\mathop{\rm s}\nolimits} i{\rm{n}}x}}{{{{\left( {\cos x - m} \right)}^2}}} \Rightarrow \,y'\left( x \right) > 0\,\,\,\forall x \in \left( {0;\pi } \right) \Leftrightarrow \,\,\dfrac{{2m\sin x + {\mathop{\rm s}\nolimits} i{\rm{n}}x}}{{{{\left( {\cos x - m} \right)}^2}}} > 0\,\,\,\forall x \in \left( {0;\pi } \right) \Leftrightarrow {\mathop{\rm s}\nolimits} {\rm{inx}}\left( {2m + 1} \right) > 0\,\,\forall x \in \left( {0;\pi } \right). Do với x \in \left( {0;\pi } \right) thì {\mathop{\rm s}\nolimits} {\rm{inx}} > 0 nên bất phương trình \left( {2m + 1} \right)\sin x > 0\,\,\,\forall x \in \left( {0;\pi } \right) \Rightarrow 2m + 1 > 0 \Rightarrow m > - \dfrac{1}{2}. Đối chiếu với điều kiện \left| m \right| \ge 1 ta nhận được m \ge 1. Chọn D. Câu hỏi 21 : Cho hàm số y=\frac{mx+2}{2x+m}, mlà tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của mđể hàm số nghịch biến trên khoảng \left( 0;\,1 \right) Tìm số phần tử của S
Đáp án: C Phương pháp giải: Hàm số y=\frac{ax+b}{cx+d} nghịch biến trên khoảng K khi \left\{ \begin{array}{l}y' < 0,\,\forall x \in K\\\frac{{ - d}}{c} \notin K\end{array} \right.. Lời giải chi tiết: Ta có {y}'=\frac{{{m}^{2}}-4}{{{\left( 2x+m \right)}^{2}}}, x\ne -\frac{m}{2} Để hàm số nghịch biến trên \left( 0;\,1 \right) \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 4 < 0\\ - \frac{m}{2} \notin \left( {0;\,1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 2 < m < 2\\m \in \left( { - \infty ;\, - 2} \right] \cup \left[ {0;\, + \infty } \right)\end{array} \right.\Leftrightarrow 0\le m<2 Với m\in \mathbb{Z} nên ta có m=\left\{ 0;\,1 \right\} Có 2 giá trị nguyên của mthỏa mãn yêu cầu bài toán. Chọn C. Câu hỏi 22 : Có bao nhiêu giá trị nguyên của m\in (-10;10) để hàm số y={{m}^{2}}{{x}^{4}}-2\left( 4m-1 \right){{x}^{2}}+1 đồng biến trên khoảng (1;\,\,+\infty )?
Đáp án: C Phương pháp giải: Để hàm số đồng biến trên \left( 1;+\infty \right)\Rightarrow y'\ge 0\,\,\forall x\in \left( 1;+\infty \right) và y'=0 tại hữu hạn điểm thuộc \left( 1;+\infty \right) Lời giải chi tiết: Ta có y'=4{{m}^{2}}{{x}^{3}}-4\left( 4m-1 \right)x=4x\left( {{m}^{2}}{{x}^{2}}-4m+1 \right). Để hàm số đồng biến trên \left( 1;+\infty \right)\Leftrightarrow y'\ge 0,\text{ }\forall x\in \left( 1;+\infty \right)\Leftrightarrow {{m}^{2}}{{x}^{2}}-4m+1\ge 0,\text{ }\forall x\in \left( 1;+\infty \right) (1) Rõ ràng m=0 thỏa mãn (1). Với m\ne 0 thì (1) \Leftrightarrow {x^2} \ge \frac{{4m - 1}}{{{m^2}}}\,\,\forall x \in \left( {1; + \infty } \right) \Leftrightarrow \frac{{4m - 1}}{{{m^2}}} \le 1 \Leftrightarrow \left\{ \begin{array}{l} m \ne 0\\ {m^2} - 4m + 1 \ge 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m \ne 0\\ \left[ \begin{array}{l} m \ge 2 + \sqrt 3 \\ m \le 2 - \sqrt 3 \end{array} \right. \end{array} \right. Vậy có 16 giá trị của m thỏa mãn yêu cầu bài toán. Chọn C.
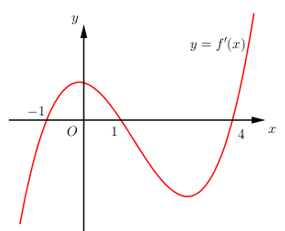
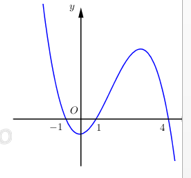
Câu hỏi 23 : Cho hàm số y=f\left( x \right). Hàm số y={f}'\left( x \right) có đồ thị như hình bên. Hàm số y=f\left( x-{{x}^{2}} \right) nghịch biến trên khoảng
Đáp án: D Phương pháp giải: Tính đạo hàm của hàm hợp, xác định khoảng đồng biến, nghịch biến dựa vào đồ thị hàm số Lời giải chi tiết: Ta có g\left( x \right)=f\left( x-{{x}^{2}} \right)\,\,\xrightarrow{{}}\,\,{g}'\left( x \right)=\left( 1-2x \right).{f}'\left( x-{{x}^{2}} \right);\,\,\forall x\in \mathbb{R}. Xét g'\left( x \right) < 0 \Leftrightarrow \left( {1 - 2x} \right).f'\left( {x - {x^2}} \right) < 0 \Leftrightarrow\left[ \begin{array}{l}\left\{ \begin{array}{l}1 - 2x > 0\\f'\left( {x - {x^2}} \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}1 - 2x < 0\\f'\left( {x - {x^2}} \right) > 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}1 - 2x > 0\\1 < x - {x^2} < 2\end{array} \right.\\\left\{ \begin{array}{l}1 - 2x < 0\\x - {x^2} \in \left( { - \,\infty ;1} \right) \cup \left( {2; + \,\infty } \right)\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < \frac{1}{2}\\{x^2} - x + 1 < 0\\{x^2} - x + 2 > 0\end{array} \right.\\\left\{ \begin{array}{l}x > \frac{1}{2}\\\left[ \begin{array}{l}{x^2} - x + 1 > 0\\{x^2} - x + 2 < 0\end{array} \right.\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x < \frac{1}{2}\\VN\\VSN\end{array} \right.\\\left\{ \begin{array}{l}x > \frac{1}{2}\\\left[ \begin{array}{l}VSN\\VN\end{array} \right.\end{array} \right.\end{array} \right. \Leftrightarrow x > \frac{1}{2}. Vậy hàm số y=g\left( x \right) nghịch biến trên khoảng \left( \frac{1}{2};+\,\infty \right). Chọn D Câu hỏi 24 : Cho hàm số y=f\left( x \right) có hàm số y=f'\left( x \right) có đồ thị hình bên. Hàm số y=f\left( -x \right) đồng biến trên khoảng :
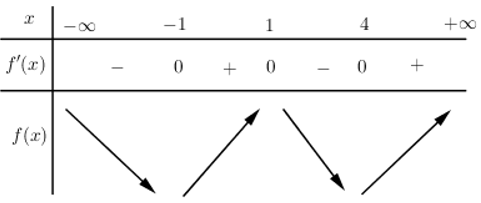
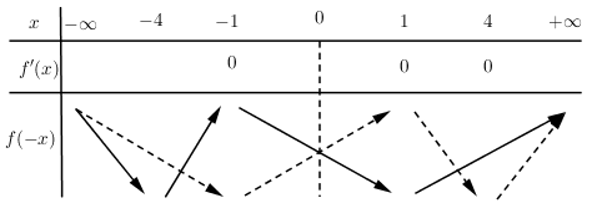
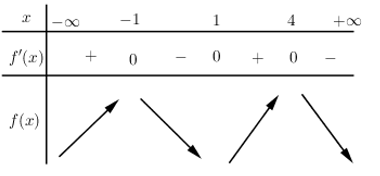
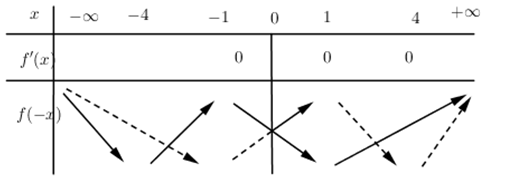
Đáp án: D Phương pháp giải: +) Xác định các điểm cực trị, các khoảng biến thiên của đồ thị hàm số y=f\left( x \right), từ đó lập BBT của của đồ thị hàm số y=f\left( x \right). +) Đồ thị hàm số y=f\left( -x \right) đối với đồ thị hàm số y=f\left( x \right) qua trục tung nên từ BBT của đồ thị hàm số y=f\left( x \right) ta lập được BBT của đồ thị hàm số y=f\left( -x \right) và suy ra các khoảng đồng biến của đồ thị hàm số y=f\left( -x \right). Lời giải chi tiết: Dựa vào đồ thị hàm số y=f'\left( x \right) ta thấy f'\left( x \right)=0\Leftrightarrow \left[ \begin{align} & x=-1 \\ & x=1 \\ & x=4 \\ \end{align} \right. \begin{align} & f'\left( x \right)>0\Leftrightarrow x\in \left( -1;1 \right)\cup \left( 4;+\infty \right) \\ & f'\left( x \right)<0\Leftrightarrow x\in \left( -\infty ;-1 \right)\cup \left( 1;4 \right) \\ \end{align} Từ đó ta lập được BBT của đồ thị hàm số y=f\left( x \right) như sau :
Đồ thị hàm số y=f\left( -x \right) đối với đồ thị hàm số y=f\left( x \right) qua trục tung nên từ BBT của đồ thị hàm số y=f\left( x \right) ta lập được BBT của đồ thị hàm số y=f\left( -x \right) như sau :
Từ BBT ta dễ thấy hàm số y=f\left( -x \right) đồng biến trên khoảng \left( -3;-1 \right). Chọn D.
Câu hỏi 25 : Cho hàm số y=f\left( x \right). Biết hàm số y=f'\left( x \right) có đồ thị như hình vẽ bên dưới. Hàm số y=f\left( 3-{{x}^{2}} \right) đồng biến trên khoảng
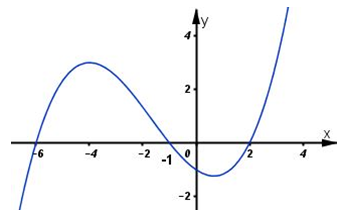
Đáp án: D Phương pháp giải: Lời giải chi tiết: Ta có \left[ f\left( 3-{{x}^{2}} \right) \right]'=-2x.f'\left( 3-{{x}^{2}} \right)>0\Leftrightarrow f’(3 – x2) trái dấu với x Ta thấy chỉ có khoảng (–1;0) là x âm và 2 < 3 – x2 < 3 do đó f’(3 – x2) > 0 (theo đồ thị) nên f(3 – x2) đồng biến trên (–1;0) Chọn D
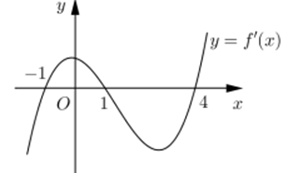
Câu hỏi 26 : Cho hàm số y=f\left( x \right). Hàm số y=f'\left( x \right) có đồ thị như hình dưới
Hàm số y=f\left( 3-x \right) nghịch biến trên khoảng:
Đáp án: B Phương pháp giải: +) Lập BBT của đồ thị hàm số y=f\left( x \right) sau đó suy ra đồ thị của hàm số y=f\left( -x \right) đối xứng với đồ thị hàm sốy=f\left( x \right) qua trục Oy. Và suy ra đồ thị hàm số y=f\left( 3-x \right) bằng cách tính tiến đồ thị hàm số y=f\left( -x \right) theo vector \left( 3;0 \right) +) Suy ra các khoảng nghịch biến của đồ thị hàm số y=f\left( 3-x \right). Lời giải chi tiết: Dựa vào đồ thị hàm số y=f'\left( x \right) ta thấy f'\left( x \right)=0\Leftrightarrow \left[ \begin{align} x=-1 \\ x=1 \\ x=4 \\ \end{align} \right. f'\left( x \right)>0\Leftrightarrow x\in \left( -\infty ;-1 \right)\cup \left( 1;4 \right);\,\,f'\left( x \right)<0\Leftrightarrow x\in \left( -1;1 \right)\cup \left( 4;+\infty \right) Từ đó ta có thể lập được BBT của đồ thị hàm số y=f\left( x \right) như sau:
Đồ thị hàm số y=f\left( 3-x \right) được vẽ bằng cách: Vẽ đồ thị hàm số y=f\left( -x \right) đối xứng với đồ thị hàm số y=f\left( x \right) qua trục Oy, sau đó tịnh tiến đồ thị hàm số y=f\left( -x \right) theo vector \left( 3;0 \right) Đồ thị hàm số y=f\left( x \right) đồng biến trên \left( -\infty ;-1 \right) và \left( 1;4 \right) nên đồ thị hàm số y=f\left( -x \right) nghịch biến trên \left( -4;-1 \right) và \left( 1;+\infty \right). \Rightarrow Đồ thị hàm số y=f\left( 3-x \right) nghịch biến trên \left( -1;2 \right) và \left( 4;+\infty \right). Chọn B. Câu hỏi 27 : Cho hàm số y=f\left( x \right). Hàm số y=f'\left( x \right) có đồ thị như hình bên. Hàm số y=f\left( 2-x \right) đồng biến trên khoảng
Đáp án: C Phương pháp giải: +) Xác định các điểm cực trị (các điểm là nghiệm của phương trình f'\left( x \right)=0), các khoảng đơn điệu của đồ thị hàm số y=f\left( x \right), từ đó lập BBT của đồ thị hàm số y=f\left( x \right). +) Từ BBT của đồ thị hàm số y=f\left( x \right) suy ra BBT của đồ thị hàm số y=f\left( -x \right) bằng cách lấy đối xứng đồ thị hàm số y=f\left( x \right) qua trục tung. +) Nhận xét đồ thị hàm số y=f\left( 2-x \right) và y=f\left( -x \right) có các khoảng đơn điệu giống nhau và rút ra kết luận. Lời giải chi tiết: Dựa vào đồ thị hàm số y=f'\left( x \right) ta suy ra đồ thị hàm số y=f\left( x \right) như sau : Ta có nhận xét đồ thị hàm số y=f\left( x \right) và đồ thị hàm số y=f\left( -x \right) đối xứng nhau qua trục tung nên ta có BBT của đồ thị hàm số y=f\left( -x \right) như sau : Đồ thị hàm số y=f\left( 2-x \right) là ảnh của phép tịnh tiến đồ thị hàm số y=f\left( -x \right) theo vector \left( 0;2 \right) nên dựa vào BBT ta thấy đáp án C đúng. Chọn C. Câu hỏi 28 : Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y=\frac{1}{3}{{\left( x+1 \right)}^{3}}+mx-\frac{27}{5{{\left( x+1 \right)}^{5}}} đồng biến trên \left( 0;+\infty \right)?
Đáp án: C Phương pháp giải: Tính y’, giải phương trình y'\ge 0\,\,\forall x\in \left( 0;+\infty \right) Lời giải chi tiết: TXĐ : x\ne -1 Ta có: y'={{\left( x+1 \right)}^{2}}+m-\frac{27}{5}.\left( -5 \right){{\left( x+1 \right)}^{-6}}={{\left( x+1 \right)}^{2}}+m+\frac{27}{{{\left( x+1 \right)}^{6}}} Áp dụng BĐT Cô-si ta có : \begin{align} {{\left( x+1 \right)}^{2}}+\frac{27}{{{\left( x+1 \right)}^{6}}}=\frac{1}{3}{{\left( x+1 \right)}^{2}}+\frac{1}{3}{{\left( x+1 \right)}^{2}}+\frac{1}{3}{{\left( x+1 \right)}^{2}}+\frac{27}{{{\left( x+1 \right)}^{6}}} \\ \,\ge 4\sqrt[4]{{{\left( \frac{1}{3}{{\left( x+1 \right)}^{2}} \right)}^{3}}.\frac{27}{{{\left( x+1 \right)}^{6}}}}=4 \\ \Rightarrow y'\ge 4+m \\ \end{align} Để đồ thị hàm số đồng biến trên \left( 0;+\infty \right)\Rightarrow y'\ge 0\,\,\forall x\in \left( 0;+\infty \right)\Rightarrow 4+m\ge 0\,\,\forall x\in \left( 0;+\infty \right)\Leftrightarrow m\ge -4 m là số nguyên âm \Rightarrow m\in \left\{ -1;-2;-3;-4 \right\} Chọn C. Câu hỏi 29 : Cho hai hàm số y=f\left( x \right),\ y=g\left( x \right). Hai hàm số y=f'\left( x \right) và y=g'\left( x \right) có đồ thị hàm như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=g'\left( x \right). Hàm số h\left( x \right)=f\left( x+6 \right)-g\left( 2x+\frac{5}{2} \right) đồng biến trên khoảng nào dưới đây?
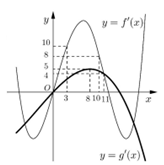
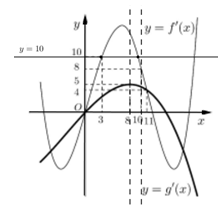
Đáp án: B Phương pháp giải: Hàm số y=f\left( x \right) đồng biến \Leftrightarrow f'\left( x \right)\ge 0. Lời giải chi tiết: Dựa vào đồ thị hàm số ta thấy đường thẳng y=10 cắt đồ thị hàm số y=f'\left( x \right) tại hai điểm phân biệt \left( 3;\ 10 \right) và \left( m;\ 10 \right) với mọi m\in \left( 8;\ 10 \right). \Rightarrow \left\{ \begin{array}{l} f'\left( {x + 6} \right) > 10\\ g'\left( {2x + \frac{5}{2}} \right) \le 5 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 3 < x + 6 < m < 8\\ 0 < 2x + \frac{5}{2} < 11 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3 < x < 2\\ - \frac{5}{4} \le x \le \frac{{17}}{4} \end{array} \right. \Leftrightarrow - \frac{5}{4} \le x < 2. Lại có h\left( x \right) đồng biến \Leftrightarrow h'\left( x \right)>0\Leftrightarrow f'\left( x+6 \right)-2g'\left( 2x+\frac{5}{2} \right)>0 Mà f'\left( x+6 \right)>10 và 2g'\left( 2x+\frac{5}{2} \right)\le -10\Rightarrow h\left( x \right) đồng biến trên \left[ -\frac{5}{4};\ 2 \right). Dựa vào các đáp án ta thấy đáp án B thỏa mãn. Chọn B. Câu hỏi 30 : Cho hàm số f\left( x \right) có bảng xét dấu của đạo hàm như sau
Hàm số y = 3f\left( {x + 2} \right) - {x^3} + 3x đồng biến trên khoảng nào dưới đây ?
Đáp án: C Phương pháp giải: Hàm số y = f\left( x \right) đồng biến trên \left( {a;b} \right) khi và chỉ khi f'\left( x \right) \ge 0\,\,\forall x \in \left( {a;b} \right) và bằng 0 tại hữu hạn điểm. Lưu ý công thức tính đạo hàm của hàm hợp. Sau đó thử từng đáp án để chọn kết quả đúng. Lời giải chi tiết: Ta có : y = 3f\left( {x + 2} \right) - {x^3} + 3x \Rightarrow y' = 3f'\left( {x + 2} \right) - 3{x^2} + 3. Xét \, - 1 < x < 0 ta có : \left\{ \begin{array}{l}1 < x + 2 < 2 \Rightarrow f'\left( {x + 2} \right) > 0\\{x^2} < 1 \Leftrightarrow {x^2} - 1 < 0\end{array} \right. \Rightarrow 3f'\left( {x + 2} \right) - 3{x^2} + 3 > 0\,\,\forall x \in \left( {0;1} \right). Vậy hàm số đã cho đồng biến trên \left( { - 1;0} \right). CHỌN C. Câu hỏi 31 : Cho hàm số y = f\left( x \right) có đồ thị hàm số y = f’\left( x \right) được cho như hình vẽ. Hàm số g\left( x \right) = - 2f\left( {2 - x} \right) + {x^2} nghịch biến trên khoảng nào?
Đáp án: D Phương pháp giải: Tính g'\left( x \right), dựa vào các đáp án xác định dấu của g'\left( x \right) trên mỗi khoảng và kết luận. Lời giải chi tiết: Ta có g'\left( x \right) = 2f'\left( {2 - x} \right) + 2x. Với x \in \left( { - 1;0} \right) ta có - 1 < x < 0 \Leftrightarrow 2 < 2 - x < 3 \Rightarrow \left\{ \begin{array}{l}x < 0\\f'\left( {2 - x} \right) < 0\end{array} \right. \Leftrightarrow 2f'\left( {2 - x} \right) + 2x < 0 \Leftrightarrow g'\left( x \right) < 0. Vậy hàm số g\left( x \right) = - 2f\left( {2 - x} \right) + {x^2} nghịch biến trên (-1 ; 0). Chọn D. Câu hỏi 32 : Tìm tất cả các giá trị nguyên dương nhỏ hơn 5 của tham số m để hàm số y = \dfrac{1}{3}{x^3} + \left( {m - 1} \right){x^2} + \left( {2m - 3} \right)x - \dfrac{2}{3} đồng biến trên \left( {1; + \infty } \right).
Đáp án: D Phương pháp giải: +) Hàm số y = f\left( x \right) đồng biến trên \left( {1; + \infty } \right) \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {1; + \infty } \right). +) Cô lập m, đưa bất phương trình về dạng f\left( x \right) \ge m\,\,\forall x \in \left( {1; + \infty } \right) \Leftrightarrow m \le \mathop {\min }\limits_{\left[ {1; + \infty } \right)} f\left( x \right). Lời giải chi tiết: Ta có y' = {x^2} + 2\left( {m - 1} \right)x + 2m - 3. Để hàm số đồng biến trên \left( {1; + \infty } \right) \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {1; + \infty } \right) \begin{array}{l} \Leftrightarrow {x^2} + 2\left( {m - 1} \right)x + 2m - 3 \ge 0\,\,\forall x \in \left( {1; + \infty } \right)\\ \Leftrightarrow {x^2} + 2m\left( {x + 1} \right) - 2x - 3 \ge 0\,\,\forall x \in \left( {1; + \infty } \right)\\ \Leftrightarrow {x^2} - 2x - 3 \ge - 2m\left( {x + 1} \right)\,\,\forall x \in \left( {1; + \infty } \right)\end{array} Do x \in \left( {1; + \infty } \right) \Rightarrow x + 1 > 0 \Leftrightarrow - 2m \le \dfrac{{{x^2} - 2x - 3}}{{x + 1}} = f\left( x \right)\,\,\forall x \in \left( {1; + \infty } \right) \Leftrightarrow - 2m \le \mathop {\min }\limits_{\left[ {1; + \infty } \right)} f\left( x \right) Xét hàm số f\left( x \right) = \dfrac{{{x^2} - 2x - 3}}{{x + 1}} trên \left[ {1; + \infty } \right) ta có: f'\left( x \right) = \dfrac{{\left( {2x - 2} \right)\left( {x + 1} \right) - {x^2} + 2x + 3}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{{{x^2} + 2x + 1}}{{{{\left( {x + 1} \right)}^2}}} = 1 > 0 \Rightarrow Hàm số đồng biến trên \left[ {1; + \infty } \right) \Rightarrow \mathop {\min }\limits_{\left[ {1; + \infty } \right)} f\left( x \right) = f\left( 1 \right) = - 2 \Leftrightarrow - 2m \le - 2 \Leftrightarrow m \ge 1. Kết hợp điều kiện đề bài m \in Z,\,\,m < 5 \Rightarrow m \in \left\{ {1;2;3;4} \right\}. Chọn D. Câu hỏi 33 : Tổng tất cả các giá trị nguyên âm của tham số m để hàm số y = {x^3} + mx - \dfrac{3}{{28{x^2}}}, đồng biến trên khoảng \left( {0; + \infty } \right) bằng:
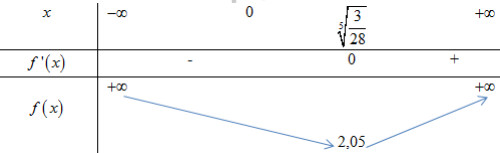
Đáp án: C Phương pháp giải: +) Tính y’. Hàm số đồng biến trên \left( {0; + \infty } \right) \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {0; + \infty } \right) và bằng 0 tại hữu hạn điểm. +) Cô lập m, đưa bất phương trình về dạng m \le f\left( x \right)\,\,\forall x \in \left( {0; + \infty } \right) \Leftrightarrow m \le \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right).. +) Xét hàm số y = f\left( x \right) trên \left( {0; + \infty } \right), lập BBT tìm \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right) Lời giải chi tiết: TXĐ: D = R\backslash \left\{ 0 \right\}. Ta có y' = 3{x^2} + m - \frac{3}{{28}}\left( { - 2\frac{1}{{{x^3}}}} \right) = 3{x^2} + m + \frac{3}{{14{x^3}}}. Để hàm số đồng biến trên khoảng \left( {0; + \infty } \right) thì y' \ge 0\,\,\forall x \in \left( {0; + \infty } \right) và bằng 0 tại hữu hạn điểm. \begin{array}{l} \Leftrightarrow 3{x^2} + m + \frac{3}{{14{x^3}}} \ge 0\,\,\forall x \in \left( {0; + \infty } \right)\\ \Leftrightarrow 3{x^2} + \frac{3}{{14{x^3}}} \ge - m\,\,\forall x \in \left( {0; + \infty } \right)\end{array} Đặt f\left( x \right) = 3{x^2} + \frac{3}{{14{x^3}}} \Rightarrow f\left( x \right) \ge - m\,\,\forall x \in \left( {0; + \infty } \right) \Leftrightarrow - m \le \mathop {\min }\limits_{\left[ {0; + \infty } \right)} f\left( x \right). Xét hàm số f\left( x \right) = 3{x^2} + \frac{3}{{14{x^3}}} trên \left( {0; + \infty } \right) ta có: f'\left( x \right) = 6x + \frac{3}{{35}}.\left( { - \frac{3}{{{x^4}}}} \right) = 6x - \frac{9}{{14{x^4}}} = 0 \Leftrightarrow 6x = \frac{9}{{14{x^4}}} \Leftrightarrow {x^5} = \frac{3}{{28}} \Leftrightarrow x = \sqrt[5]{{\frac{3}{{28}}}}. BBT:
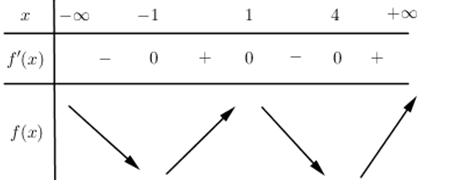
\Rightarrow - m \le 2,05 \Leftrightarrow m \ge - 2,05. Mà m là số nguyên âm \Rightarrow m \in \left\{ { - 2; - 1} \right\}. Vậy tổng các giá trị của m thỏa mãn yêu cầu bài toán là -2 – 1 = -3. Chọn C. Câu hỏi 34 : Cho hàm số y = f\left( x \right). Hàm số y = f'\left( x \right) có bảng xét dấu như sau:
Đáp án: B Phương pháp giải: +) Sử dụng công thức đạo hàm hàm hợp tính đạo hàm của hàm số g\left( x \right) = f\left( {{x^2} + 2x} \right). +) Hàm số y = g\left( x \right) nghịch biến trên \left( {a;b} \right) \Leftrightarrow g'\left( x \right) \le 0\,\,\forall x \in \left( {a;b} \right) và bằng 0 tại hữu hạn điểm. +) Dựa vào các đáp án, thay giá trị của {x_0} thuộc từng khoảng, tính g'\left( {{x_0}} \right) và loại đáp án. Lời giải chi tiết: Đặt g\left( x \right) = f\left( {{x^2} + 2x} \right) ta có g'\left( x \right) = \left( {2x + 2} \right)f'\left( {{x^2} + 2x} \right) = 2\left( {x + 1} \right)f'\left( {{x^2} + 2x} \right). Hàm số y = g\left( x \right) nghịch biến trên \left( {a;b} \right) \Leftrightarrow g'\left( x \right) \le 0\,\,\forall x \in \left( {a;b} \right) và bằng 0 tại hữu hạn điểm. Xét đáp án A ta có : g'\left( {\frac{1}{2}} \right) = 3f'\left( {\frac{5}{4}} \right) > 0 \Rightarrow Loại đáp án A. Xét đáp án C ta có : g'\left( {\frac{{ - 3}}{2}} \right) = 2f'\left( 0 \right) > 0 \Rightarrow Loại đáp án C. Xét đáp án D ta có g'\left( { - \frac{7}{2}} \right) = - 5f'\left( {\frac{{21}}{4}} \right) > 0 \Rightarrow Loại đáp án D. Chọn B. Câu hỏi 35 : Cho hàm số f\left( x \right) có bảng biến thiên như sau : Hàm số y = {\left( {f\left( x \right)} \right)^3} - 3.{\left( {f\left( x \right)} \right)^2} nghịch biến trên khoảng nào dưới đây ?
Đáp án: C Phương pháp giải: +) Sử dụng công thức đạo hàm hàm hợp tính y'. +) Lấy {x_0} thuộc từng khoảng đáp án, kiểm tra y'\left( {{x_0}} \right) và kết luận. Lời giải chi tiết: Ta có : y' = 3{f^2}\left( x \right)f'\left( x \right) - 6f\left( x \right)f'\left( x \right) = 3f\left( x \right)f'\left( x \right)\left[ {f\left( x \right) - 2} \right] Với x = 2,5 \Rightarrow y'\left( {2,5} \right) = 3f\left( {2,5} \right)f'\left( {2,5} \right)\left[ {f\left( {2,5} \right) - 2} \right] Ta có : \left\{ \begin{array}{l}1 < f\left( {2,5} \right) < 2 \Rightarrow \left\{ \begin{array}{l}f\left( {2,5} \right) > 0\\f\left( {2,5} \right) - 2 < 0\end{array} \right.\\f'\left( {2,5} \right) > 0\end{array} \right. \Rightarrow y'\left( {2,5} \right) < 0 \Rightarrow Loại các đáp án A, B và D. Chọn C. Câu hỏi 36 : Cho hàm số f\left( x \right) có đồ thị của hàm số y = f'\left( x \right) như hình vẽ:
Hàm số y = f\left( {2x - 1} \right) + \dfrac{{{x^3}}}{3} + {x^2} - 2x nghịch biến trên khoảng nào sau đây:
Đáp án: A Phương pháp giải: Hàm số y = f\left( x \right) nghịch biến trên \left( {a;b} \right) \Leftrightarrow f'\left( x \right) \le 0\,\,\forall x \in \left( {a;b} \right) và bằng 0 tại hữu hạn điểm. Lời giải chi tiết: Ta có y' = 2f'\left( {2x - 1} \right) + {x^2} + 2x - 2. Ta tìm tập hợp các giá trị của x làm cho y' < 0. Lấy x = - 5 \Rightarrow y'\left( { - 5} \right) = f'\left( { - 11} \right) + 13 > 0 \Rightarrow Loại đáp án B. Lấy x = 5 \Rightarrow y'\left( 5 \right) = f'\left( 9 \right) + 33 > 0 \Rightarrow Loại đáp án C. Lấy x = 7 \Rightarrow y'\left( 7 \right) = f'\left( {13} \right) + 61 > 0 \Rightarrow Loại đáp án D. Chọn A. Câu hỏi 37 : Cho hàm số y = \left| {{x^3} - mx + 1} \right|. Gọi S là tập tất cả các số tự nhiên m sao cho hàm số đồng biến trên \left[ {1; + \infty } \right). Tìm số phần tử của S.
Đáp án: A Phương pháp giải: Lời giải chi tiết: Xét hàm số y = f\left( x \right) = {x^3} - mx + 1,\,\,\,f'\left( x \right) = 3{x^2} - m Nhận xét: Đồ thị hàm số y = \left| {f\left( x \right)} \right| = \left| {{x^3} - mx + 1} \right| được dựng từ đồ thị hàm số y = f\left( x \right) bằng cách giữ lại phần đồ thị phía trên trục Ox và lấy đối xứng phần phía dưới Ox qua Ox (xóa bỏ phần đồ thị của y = f\left( x \right) nằm phía dưới Ox). TH1: Với m = 0 ta có: Hàm số y = f\left( x \right) = {x^3} + 1 đồng biến trên \mathbb{R} Có f\left( 1 \right) = 2 > 0 \Rightarrow Hàm số y = \left| {f\left( x \right)} \right| = \left| {{x^3} - mx + 1} \right| đồng biến trên \left[ {1; + \infty } \right) \Rightarrow m = 0: thỏa mãn. TH2: Với m > 0 ta có: f'\left( x \right) = 0 có 2 nghiệm phân biệt {x_1},\,{x_2}\left( {{x_1} < {x_2}} \right) Để hàm số y = \left| {{x^3} - mx + 1} \right| đồng biến trên \left[ {1; + \infty } \right) thì \left\{ \begin{array}{l}m > 0\\{x_1} < {x_2} \le 1\\f\left( 1 \right) \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\frac{{ - m}}{3} + 1 \ge 0\\2 - m \ge 0\end{array} \right. \Leftrightarrow 0 < m \le 2 Mà m \notin \mathbb{N} \Rightarrow m \in \left\{ {1;2} \right\} Vậy, S = \left\{ {0;\;1;\;2} \right\}. Số phần tử của S là 3. Chọn: A Câu hỏi 38 : Cho hàm số y = f\left( x \right) liên tục trên \mathbb{R} và có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số m để phương trình f\left( {\left| {\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}}} \right|} \right) = f\left( {{m^2} + 4m + 4} \right) có nghiệm?
Đáp án: D Phương pháp giải: + Đặt \dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}} = t, biến đổi đưa về dạng a\sin x + b\cos x = c, phương trình này có nghiệm khi {a^2} + {b^2} \ge {c^2} từ đó ta tìm ra được điều kiện của t. + Dựa vào đồ thị hàm số để xác định điều kiện nghiệm của phương trình f\left( x \right) = f\left( {\left| t \right|} \right) Từ đó suy ra điều kiện có nghiệm của phương trình đã cho. Chú ý rằng nếu hàm f\left( t \right) đồng biến (hoặc nghịch biến) trên \left( {a;b} \right) thì phương trình f\left( u \right) = f\left( v \right) nếu có nghiệm thì đó là nghiệm duy nhất trên \left( {a;b} \right) \Leftrightarrow u = v. Lời giải chi tiết: Vì - 1 \le \sin x \le 1; - 1 \le \cos x \le 1 nên 2\cos x - \sin x > - 3 \Rightarrow 2\cos x - \sin x + 4 > 0 Đặt \dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}} = t \Leftrightarrow 3\sin x - \cos x - 1 = t\left( {2\cos x - \sin x + 4} \right) \Leftrightarrow \cos x\left( {2t + 1} \right) - \sin x\left( {t + 3} \right) = - 4t - 1 Phương trình trên có nghiệm khi {\left( {2t + 1} \right)^2} + {\left( {t + 3} \right)^2} \ge {\left( { - 4t - 1} \right)^2} \Leftrightarrow 5{t^2} + 10t + 10 \ge 16{t^2} + 8t + 1 \Leftrightarrow 11{t^2} - 2t - 9 \le 0 \Leftrightarrow - \dfrac{9}{{11}} \le t \le 1 \Rightarrow 0 \le \left| t \right| \le 1 Từ đồ thị hàm số ta thấy hàm số f\left( x \right) đồng biến trên \left( {0;1} \right) Nên phương trình f\left( x \right) = f\left( {\left| t \right|} \right) với t \in \left[ {0;1} \right] có nghiệm duy nhất khi x = \left| t \right| \Rightarrow x \ge 0 Do đó phương trình f\left( {\left| {\dfrac{{3\sin x - \cos x - 1}}{{2\cos x - \sin x + 4}}} \right|} \right) = f\left( {{m^2} + m + 4} \right) có nghiệm \Leftrightarrow \left| t \right| = {m^2} + 4m + 4 có nghiệm với 0 \le \left| t \right| \le 1 \Leftrightarrow 0 \le {m^2} + 4m + 4 \le 1 \Leftrightarrow {\left( {m + 2} \right)^2} \le 1 \Leftrightarrow - 3 \le m \le - 1 Mà m \in \mathbb{Z} nên m \in \left\{ { - 3; - 2; - 1} \right\}. Vậy có 3 giá trị của m thỏa mãn yêu cầu. Chọn D. Câu hỏi 39 : Cho hàm số y = {\left( {x + a} \right)^3} + {\left( {x + b} \right)^3} - {x^3} với a,b là các số thực . Khi hàm số đồng biến trên R , hãy tìm giá trị nhỏ nhất của biểu thức A = 4\left( {{a^2} + {b^2}} \right) - \left( {a + b} \right) - ab
Đáp án: B Phương pháp giải: - Tính y'. - Hàm số đồng biến trên \mathbb{R} \Leftrightarrow y' \ge 0, \forall x \in \mathbb{R} - Biến đổi A về làm xuất hiện hằng đẳng thức và đánh giá GTNN. Lời giải chi tiết: TXĐ D = \mathbb{R}. Ta có y' = 3{\left( {x + a} \right)^2} + 3{\left( {x + b} \right)^2} - 3{x^2} = 3\left( {{x^2} + 2\left( {a + b} \right)x + {a^2} + {b^2}} \right) Để hàm số đồng biến trên \mathbb{R} \Leftrightarrow y' \ge 0, \forall x \in \mathbb{R} \Leftrightarrow {x^2} + 2\left( {a + b} \right)x + {a^2} + {b^2} \ge 0,\,\,\forall x \in \mathbb{R} \Leftrightarrow \Delta ' = 2ab \le 0 \Leftrightarrow ab \le 0 Khi đó A = 4{\left( {a + b} \right)^2} - \left( {a + b} \right) - 9ab = {\left( {2\left( {a + b} \right) - \dfrac{1}{4}} \right)^2} - 9ab - \dfrac{1}{{16}} \ge - \dfrac{1}{{16}},\,\,\forall ab \le 0. Dấu bằng xảy ra khi \left\{ \begin{array}{l}2\left( {a + b} \right) - \dfrac{1}{4} = 0\\ab = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = \dfrac{1}{8},b = 0\\a = 0,b = \dfrac{1}{8}\end{array} \right.. Vậy MinA = - \dfrac{1}{{16}} Chọn B. Câu hỏi 40 : Cho hàm số bậc ba y = f\left( x \right), hàm số y = f'\left( x \right) có đồ thị như hình vẽ. Hỏi hàm số g\left( x \right) = f\left( { - x - {x^2}} \right) nghịch biến trên khoảng nào dưới đây?
Đáp án: B Phương pháp giải: - Tính g'\left( x \right). - Xét dấu g'\left( x \right) trong từng khoảng đưa ra ở mỗi đáp án và kết luận. Lời giải chi tiết: Ta có: g\left( x \right) = f\left( { - x - {x^2}} \right) \Rightarrow g'\left( x \right) = - \left( {2x + 1} \right)f'\left( { - x - {x^2}} \right). Đáp án A: Trong khoảng \left( { - 2; - 1} \right) ta có: +) - \left( {2x + 1} \right) > 0 +) - 2 < - x - {x^2} < 0 nên f'\left( { - x - {x^2}} \right) > 0 Do đó g'\left( x \right) > 0 hay hàm số y = g\left( x \right) đồng biến trong khoảng này. Loại A. Đáp án B: Trong khoảng \left( {1;2} \right) ta có: +) - \left( {2x + 1} \right) < 0 +) - 6 < - x - {x^2} < - 2 nên f'\left( { - x - {x^2}} \right) > 0. Do đó g'\left( x \right) < 0 hay hàm số y = g\left( x \right) nghịch biến trong khoảng này. Chọn B.
|













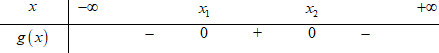
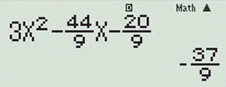
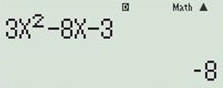

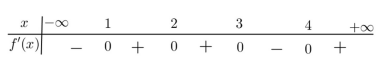
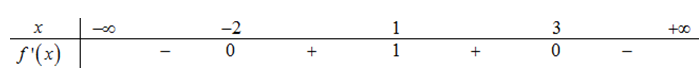 Hàm số
Hàm số