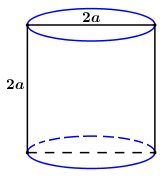
40 bài tập trắc nghiệm mặt trụ mức độ thông hiểuLàm bàiCâu hỏi 1 : Cho hình trụ có chiều cao bằng \(4a\), diện tích xung quanh bằng \(2\pi {a^2}\). Tìm bán kính đáy của hình trụ đó.
Đáp án: D Phương pháp giải: Diện tích xung quanh hình trụ có chiều cao \(h\), bán kính đáy \(R\) là: \({S_{xq}} = 2\pi Rh\). Lời giải chi tiết: Ta có : \({S_{xq}} = 2\pi Rh \Leftrightarrow R = \dfrac{{{S_{xq}}}}{{2\pi h}} = \dfrac{{2\pi {a^2}}}{{2\pi .4a}} = \dfrac{a}{4}\). Chọn D. Câu hỏi 2 : Thiết diện đi qua trục của một hình trụ là một hình vuông có độ dài cạnh bằng \(a\). Tính thể tích khối trụ đó.
Đáp án: B Phương pháp giải: - Từ giả thiết thiết diện qua trục của hình trụ là một hình vuông xác định bán kính đáy và chiều cao của khối trụ. - Áp dụng công thức tính thể tích khối trụ có chiều cao \(h\), bán kính đáy \(r\)là \(V = \pi {r^2}h\). Lời giải chi tiết:
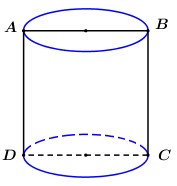
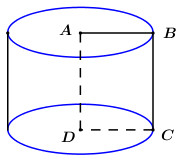
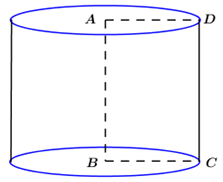
Giả sử thiết diện qua trục của hình trụ là hình vuông \(ABCD\) như hình vẽ, khi đó khối trụ đã cho có chiều cao \(h = AD = a\), bán kính đáy \(r = \dfrac{1}{2}AB = \dfrac{a}{2}\). Khi đó thể tích khối trụ là \(V = \pi {r^2}h = \pi {\left( {\dfrac{a}{2}} \right)^2}.a = \dfrac{{\pi {a^3}}}{4}.\) Chọn B. Câu hỏi 3 : Cho hình trụ có bán kính đáy bằng \(1\) và chiều cao bằng \(3\). Thiết diện của hình trụ cắt bởi mặt phẳng qua trục của nó có diện tích bằng:
Đáp án: D Phương pháp giải: Thiết diện qua trục của hình trụ có chiều cao \(h\), bán kính đáy \(r\) là hình chữ nhật có kích thước \(h \times 2r\). Lời giải chi tiết:
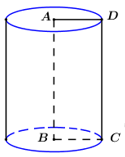
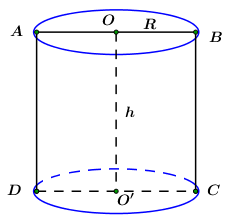
Giả sử thiết diện qua trục là hình chữ nhật \(ABCD\), ta có \(AD = h = 3,\,\,AB = 2r = 2\). Vậy \({S_{ABCD}} = 3.2 = 6\). Chọn D. Câu hỏi 4 : Cho hình trụ có chiều cao bằng \(5a\), cắt hình trụ bởi mặt phẳng song song với trục và cách trục một khoảng bằng \(3a\) được thiết diện có diện tích bằng \(20{a^2}\). Thể tích khối trụ là:
Đáp án: C Phương pháp giải: - Sử dụng định lí Pytago tính bán kính đáy của hình trụ. - Thể tích khối trụ có chiều cao \(h\), bán kính đáy \(R\) là \(V = \pi {R^2}h\). Lời giải chi tiết:
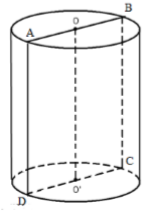
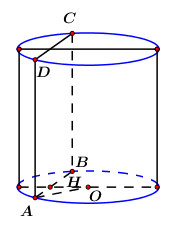
Giả sử thiết diện là hình chữ nhật \(ABCD\). Ta có: \({S_{ABCD}} = AB.BC \Rightarrow 20{a^2} = AB.5a \Leftrightarrow AB = 4a\) \( \Rightarrow AH = 2a\). Gọi \(O,\,\,O'\) lần lượt là tâm hai đáy của hình trụ, \(H\) là trung điểm của \(AB\). Ta có \(\left\{ \begin{array}{l}OH \bot AB\\OH \bot BC\end{array} \right. \Rightarrow OH \bot \left( {ABCD} \right) \Rightarrow OH = 3a\). Áp dụng định lí Pytago trong tam giác vuông \(OAH\) ta có: \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {9{a^2} + 4{a^2}} = a\sqrt {13} \). Vậy thể tích khối trụ là \(V = \pi .O{A^2}.BC = \pi .{\left( {a\sqrt {13} } \right)^2}.5a = 65\pi {a^3}\). Chọn C. Câu hỏi 5 : Tính diện tích toàn phần \({S_{tp}}\) của hình trụ tạo thành khi quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\), biết \(AB = 5\), \(BC = 2\).
Đáp án: B Phương pháp giải: - Quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta thu được khối trụ có chiều cao \(h = AB\), bán kính đáy \(r = BC\). - Diện tích toàn phần của hình trụ có chiều cao \(h\), bán kính đáy \(r\) là \(V = \pi {r^2}h + 2\pi {r^2}\). Lời giải chi tiết: Quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta thu được khối trụ có chiều cao \(h = AB = 5\), bán kính đáy \(r = BC = 2\). Vậy diện tích toàn phần của hình trụ là \(V = \pi {r^2}h + 2\pi {r^2} = \pi {.2^2}.5 + 2\pi {.2^2} = 28\pi \). Chọn B. Câu hỏi 6 : Cắt hình trụ bởi mặt phẳng \(\left( \alpha \right)\) vuông góc với mặt đáy, ta được thiết diện là hình vuông có diện tích bằng 16. Khoảng cách từ tâm đường tròn đáy của hình trụ đến mặt phẳng \(\left( \alpha \right)\) bằng 3. Thể tích khối trụ bằng:
Đáp án: B Phương pháp giải: Thể tích khối nón có bán kính đáy \(R\) và đường cao \(h\) là: \(V = \pi {R^2}h.\) Lời giải chi tiết:
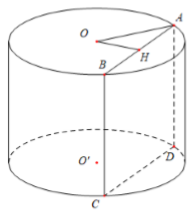
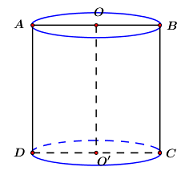
Ta có \(ABCD\) là hình vuông \( \Rightarrow {S_{ABCD}} = A{B^2} = 16\) \( \Rightarrow AB = AD = 4\) Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB\) Lại có: \(\left( {ABCD} \right)\) vuông góc với mặt phẳng đáy \( \Rightarrow OH \bot AD\) \( \Rightarrow OH \bot \left( {ABCD} \right)\) \( \Rightarrow d\left( {O;\,\,\left( {ABCD} \right)} \right) = OH = 3\) Áp dụng định lý Pitago cho \(\Delta OAH\) vuông tại \(H\) ta có: \(OA = \sqrt {O{H^2} + {{\left( {\dfrac{{AB}}{2}} \right)}^2}} = \sqrt {{3^2} + {2^2}} = \sqrt {13} \) Khi đó ta có thể tích của hình trụ đã cho là: \(V = \pi {R^2}h = \pi .O{A^2}.AD = \pi .13.4 = 52\pi .\) Chọn B. Câu hỏi 7 : Trong không gian, cho hình chữ nhật ABCD, \(AB = a\), \(AC = 2a\). Khi quay hình chữ nhật ABCD quanh cạnh AD thì đường gấp khúc ABCD tạo thành một hình trụ. Diện tích xung quanh của hình trụ đó bằng:
Đáp án: D Phương pháp giải: - Xác định đáy, chiều cao của hình trụ. - Áp dụng công thức tính diện tích xung quanh hình trụ: \(S = 2\pi rh\). Lời giải chi tiết:
Quay hình chữ nhật ABCD quanh cạnh AD ta được hình trụ có bán kính là \(r = AB = a\) và chiều cao là \(h = BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \). Vây diện tích xung quanh hình trụ:\(S = 2\pi rh = 2\pi a.a\sqrt 3 = 2\sqrt 3 \pi {a^2}.\) Chọn D. Câu hỏi 8 : Cho hình chữ nhật \(ABCD\) có \(AB = 4\) và \(AD = 3.\) Thể tích của khối trụ được tạo thành khi quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) bằng
Đáp án: A Phương pháp giải: - Khi quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta được khối trụ có chiều cao \(h = AB\), bán kính đáy \(r = AD\). - Thể tích khối trụ có chiều cao \(h\), bán kính đáy \(r\) là \(V = \pi {r^2}h\). Lời giải chi tiết: Khi quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta được khối trụ có chiều cao \(h = AB = 4\), bán kính đáy \(r = AD = 3\). Vậy thể tích khối trụ là \(V = \pi {r^2}h = \pi {.3^2}.4 = 36\pi \). Chọn A. Câu hỏi 9 : Một cái nồi có dạng hình trụ có chiều cao 60cm và diện tích đáy là \(900\pi \,\,c{m^2}\). Hỏi cần miếng kim loại hình chữ nhật có kích thước bao nhiêu để làm thân nồi?
Đáp án: B Phương pháp giải: - Tính bán kính đáy của hình trụ, sử dụng công thức tính diện tích hình tròn đáy: \(S = \pi {R^2}\). - Áp dụng công thức tính diện tích xung quanh hình trụ có chiều cao \(h\), bán kính đáy \(R\)là \({S_{xq}} = 2\pi Rh\). Lời giải chi tiết: Ta có hình trụ có diện tích đáy là \(S = \pi {R^2} = 900\pi \Leftrightarrow R = 30\,\,cm\). Diện tích xung quanh hình trụ là \(S = 2\pi Rh = 2\pi .30.60 = 60\pi .60\,\,\left( {c{m^2}} \right).\) Vậy cần miếng kim loại hình chữ nhật chiều dài \(60\pi cm\) và chiều rộng \(60\, cm\) Chọn B. Câu hỏi 10 : Thiết diện qua trục của hình trụ là một hình chữ nhật có diện tích bằng 10. Diện tích xung quanh của hình trụ đó bằng:
Đáp án: A Phương pháp giải: Diện tích xung quanh của hình trụ có bán kính đáy \(r\) và chiều cao \(h\) là: \({S_{xq}} = 2\pi rh.\) Lời giải chi tiết:
Ta có: \({S_{ABCD}} = AB.AD = 2rh = 10.\) \( \Rightarrow {S_{xq}} = 2\pi rh = 10\pi .\) Chọn A. Câu hỏi 11 : Cho khối trụ có chiều cao \(h = 2\) và bán kính mặt đáy \(r = 3.\) Thể tích của khối trụ đã cho bằng:
Đáp án: B Phương pháp giải: Thể tích khối trụ có chiều có \(h\) và bán kính đáy \(r\) là \(V = \pi {r^2}h.\) Lời giải chi tiết: Thể tích khối trụ đã cho là: \(V = \pi {r^2}h = \pi {.3^2}.2 = 18\pi .\) Chọn B. Câu hỏi 12 : Hình trụ có bán kính đáy bằng \(a\) và thiết diện qua trục là hình vuông, diện tích xung quanh hình trụ đó bằng:
Đáp án: D Phương pháp giải: Sử dụng dữ kiện thiết diện qua trục là hình vuông để tìm chiều cao hình trụ. Áp dụng công thức tính diện tích xung quanh hình trụ có chiều cao h, bán kính đáy r là: \({S_{xq}} = 2\pi rh\). Lời giải chi tiết: Vì thiết diện qua trục là hình vuông nên \(h = 2r = 2a.\) Vậy diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh = 2\pi .a.2a = 4\pi {a^2}.\) Chọn D. Câu hỏi 13 : Khối trụ tròn xoay có thể tích bằng \(144\pi \) và bán kính đáy bằng 6. Đường sinh của khối trụ bằng:
Đáp án: A Phương pháp giải: - Khối trụ có đường sinh bằng chiều cao. - Sử dụng công thức tính thể tích khối trụ có chiều cao h, bán kính đáy r là \(V = \pi {r^2}h\). Lời giải chi tiết: Ta có \(V = \pi {r^2}h \Leftrightarrow 144\pi = \pi {.6^2}.h \Leftrightarrow h = 4\). Vậy đường sinh của khối trụ bằng 4. Chọn A. Câu hỏi 14 : Tính thể tích khối trụ có có bán kính đáy bằng 2, đường cao bằng 3.
Đáp án: C Phương pháp giải: Công thức tính thể tích của khối trụ có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \pi {R^2}h.\) Lời giải chi tiết: Thể tích khối trụ có có bán kính đáy bằng 2, đường cao bằng 3 là: \(V = \pi {R^2}h = \pi {.2^2}.3 = 12\pi .\) Chọn C. Câu hỏi 15 : Trong không gian, cho hình chữ nhật \(ABCD\) có \(AB = 4,\,AC = 5\). Gọi \(M,N\) lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta thu được một hình trụ. Tính diện tích toàn phần \({S_{tp}}\) của hình trụ đó.
Đáp án: D Phương pháp giải: Sử dụng công thức tính diện tích toàn phần của hình trụ: \({S_{tp}} = 2\pi Rh + 2\pi {R^2}\), trong đó \(R,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ. Lời giải chi tiết:
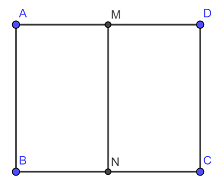
Quay hình chữ nhật ABCD quanh trục MN ta nhận được khối trụ có chiều cao \(h = AB\), bán kính đáy \(R = AM = \dfrac{1}{2}AD\). Áp dụng định lí Pytago trong tam giác vuông ACD ta có: \(AD = \sqrt {A{C^2} - A{B^2}} = \sqrt {{5^2} - {4^2}} = 3\). Hình trụ thu được có bán kính đáy \(R = \dfrac{{AD}}{2} = \dfrac{3}{2}\), đường cao \(h = AB = 4\), có diện tích toàn phần là: \({S_{tp}} = 2\pi Rh + 2\pi {R^2} = 2\pi .\dfrac{3}{2}.4 + 2\pi .{\left( {\dfrac{3}{2}} \right)^2} = \dfrac{{33}}{2}\pi \). Chọn D. Câu hỏi 16 : Cho hình trụ có thiết diện qua trục là hình vuông có cạnh bằng \(2a\). Thể tích của khối trụ giới hạn bởi hình trụ đã cho bằng:
Đáp án: D Phương pháp giải: - Xác định chiều cao và bán kính đáy của khối trụ. - Thể tích khối trụ chiều cao \(h\), bán kính đáy \(r\) là \(V = \pi {r^2}h\). Lời giải chi tiết:
Hình trụ có thiết diện qua trục là hình vuông có cạnh bằng \(2a\) nên có chiều cao \(h = 2a\) và bán kính đáy \(r = a\) . Vậy thể tích khối trụ là \(V = \pi {r^2}h = \pi .{a^2}.a = 2\pi {a^3}\). Chọn D. Câu hỏi 17 : Cho một hình trụ tròn xoay và hình vuông \(ABCD\) cạnh \(a\) có hai đỉnh liên tiếp \(A,\,\,B\) nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng \(ABCD\) tạo với đáy hình trụ góc \({45^0}\). Tính diện tích xung quanh hình trụ?
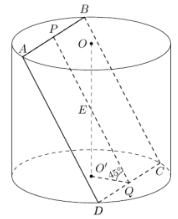
Đáp án: D Phương pháp giải: - Gọi \(P,\,\,Q,\,\,E\) lần lượt là trung điểm của \(AB,\,\,CD,\,\,OO'\). Xác định góc giữa \(\left( {ABCD} \right)\) và mặt đáy. - Sử dụng tỉ số lượng giác và định lí Pytago tính chiều cao \(h\) và bán kính đáy \(r\) của hình trụ. - Diện tích xung quanh của hình trụ có chiều cao \(h\) và bán kính đáy \(r\) là \({S_{xq}} = 2\pi rh\). Lời giải chi tiết:
Gọi \(P,\,\,Q,\,\,E\) lần lượt là trung điểm của \(AB,\,\,CD,\,\,OO'\). Dễ thấy góc giữa \(\left( {ABCD} \right)\) và mặt đáy là \(\angle O'QE = {45^0}\). Ta có: \(EQ = \dfrac{1}{2}BC = \dfrac{a}{2}\), tam giác \(O'EQ\) vuông cân tại \(O'\) nên \(O'Q = O'E = \dfrac{{EQ}}{{\sqrt 2 }} = \dfrac{a}{{2\sqrt 2 }}\). \( \Rightarrow OO' = 2O'E = \dfrac{a}{{\sqrt 2 }}\), bán kính mặt trụ là: \(r = O'C = \sqrt {O'{Q^2} + Q{C^2}} = \sqrt {{{\left( {\dfrac{a}{{2\sqrt 2 }}} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{4}\). Vậy diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi rh = 2\pi .\dfrac{{a\sqrt 6 }}{4}.\dfrac{{a\sqrt 2 }}{2} = \dfrac{{\pi {a^2}\sqrt 3 }}{2}\). Chọn D. Câu hỏi 18 : Hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng 20 cm. Thể tích của khối trụ tương ứng bằng:
Đáp án: D Phương pháp giải: Công thức tính thể tích của khối trụ có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \pi {R^2}h.\) Lời giải chi tiết:
Hình trụ có thiết diện qua trục là một hình vuông có cạnh bằng 20 cm \(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}h = 20\,cm\\2R = 20\,cm\end{array} \right. \Rightarrow \left\{ \begin{array}{l}h = 20\,\,cm\\R = 10\,\,cm\end{array} \right.\\ \Rightarrow V = \pi {R^2}h = \pi {.10^2}.20 = 2000\pi \,\,c{m^3}.\end{array}\) Chọn D. Câu hỏi 19 : Cho hình trụ có thể tích bằng \(48\pi \) và độ dài đường sinh bằng 3. Tìm bán kính đáy của hình trụ.
Đáp án: C Phương pháp giải: - Hình trụ có đường sinh l bằng chiều cao h. - Thể tích khối trụ có chiều cao h, bán kính đáy r là \(V = \pi {r^2}h\). Lời giải chi tiết: Hình trụ có đường sinh l = 3 nên có đường cao h = 3. Gọi r là bán kính đường tròn đáy của hình trụ. Theo bài ra ta có: \(V = \pi {r^2}h \Leftrightarrow 48\pi = \pi .{r^2}.3 \Leftrightarrow r = 4.\) Chọn C. Câu hỏi 20 : Cho khối trụ có chiều cao \(h = 8\), bán kính đường tròn đáy bằng 6, cắt khối trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng 4. Diện tích thiết diện tạo thành là:
Đáp án: C Phương pháp giải: - Nhận xét thiết diện là hình chữ nhật. - Sử dụng định lí Pytago xác định các kích thước của hình chữ nhật. - Hình chữ nhật có kích thước \(a \times b\) thì có diện tích \(S = a.b\). Lời giải chi tiết:
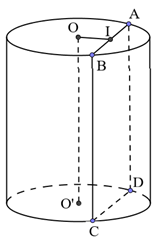
Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục một khoảng bằng \(4 < R\,\,\left( {R = 6} \right)\)\( \Rightarrow \) Thiết diện là hình chữ nhật. Giả sử thiết diện là hình chữ nhật ABCD (như hình vẽ), gọi I là trung điểm của AB. Theo đề bài ta có: \(OI = d\left( {OO';\left( {ABCD} \right)} \right) = 4,\) \(BC = h = 8,\,\,R = 6\) Tam giác OIA vuông tại I \( \Rightarrow IA = \sqrt {O{A^2} - O{I^2}} = \sqrt {{6^2} - {4^2}} = 2\sqrt 5 \)\( \Rightarrow AB = 4\sqrt 5 \) Diện tích của thiết diện là:\({S_{ABCD}} = AB.BC = 4\sqrt 5 .8 = 32\sqrt 5 \). Chọn C. Câu hỏi 21 : Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt bằng \(1\,m\) và \(1,2\,m.\) Chủ cơ sở dự định làm một bể nước mới, hình trụ, có cùng chiều cao và có thể tích bằng tổng thể tích của hai bể nước trên. Bán kính đáy của bể nước dự định làm gần nhất với kết quả nào dưới đây?
Đáp án: D Phương pháp giải: Lời giải chi tiết: Chọn D. Câu hỏi 22 : Cho khối trụ \(\left( T \right)\) có bán kính đáy bằng 4 và diện tích xung quanh bằng \(16\pi \). Tính thể tích \(V\) của khối trụ \(\left( T \right)\).
Đáp án: D Phương pháp giải: Diện tích xung quanh của hình trụ có chiều cao \(h\) và bán kính đáy \(r\) là \({S_{xq}} = 2\pi rh\) Tìm chiều cao của hình trụ. Khi đó, thể tích của khối trụ được tính bởi công thức \(V = \pi {r^2}h\) Lời giải chi tiết: Khối trụ đã cho có bán kính đáy \(r = 4\) và chiều cao bằng \(h\). Diện tích xung quanh của hình trụ bằng \(16\pi \) nên \(2\pi rh = 16\pi \Rightarrow h = 2\) Vậy thể tích của khối trụ đã cho là : \(V = \pi {r^2}h = \pi {.4^2}.2 = 32\pi \). Chọn D. Câu hỏi 23 : Cho hình trụ có bán kính đáy bằng \(3.\) Biết rằng khi cắt hình trụ đã cho bởi một mặt phẳng qua trục, thiết diện thu được là một hình vuông. Diện tích xung quanh của hình trụ đã cho bằng
Đáp án: B Phương pháp giải: - Thiết diện qua trục là hình vuông nên \(h = 2r\) với \(h,\,\,r\) lần lượt là chiều cao và bán kính đáy hình trụ. - Diện tích xung quanh của hình trụ có chiều cao \(h\), bán kính đáy \(r\) là \({S_{xq}} = 2\pi rh\). Lời giải chi tiết: Vì thiết diện qua trục là hình vuông nên chiều cao của hình trụ là \(h = 2r = 6\) (với \(r\) là bán kính đáy của hình trụ). Vậy diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi rh = 2\pi .3.6 = 36\pi \). Chọn B. Câu hỏi 24 : Cắt một hình trụ bởi mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh bằng \(3a\). Tính diện tích toàn phần của hình trụ đã cho.
Đáp án: B Phương pháp giải: - Cắt một hình trụ bởi mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh hình vuông bằng chiều cao hình trụ và gấp đôi bán kính đáy hình trụ. - Diện tích toàn phần hình trụ có chiều cao \(h\), bán kính đáy \(r\) là \({S_{tp}} = 2\pi r\left( {r + h} \right)\). Lời giải chi tiết: Gọi \(h\) và \(r\) lần lượt là chiều cao và bán kính đáy của hình trụ. Cắt một hình trụ bởi mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông có cạnh hình vuông bằng chiều cao hình trụ và gấp đôi bán kính đáy hình trụ, suy ra \(h = 2r = 3a \Rightarrow r = \dfrac{{3a}}{2}\). Vậy diện tích toàn phần hình trụ là: \({S_{tp}} = 2\pi r\left( {r + h} \right)\)\( = 2\pi .\dfrac{{3a}}{2}\left( {\dfrac{{3a}}{2} + 3a} \right) = \dfrac{{27\pi {a^2}}}{2}\). Chọn B. Câu hỏi 25 : Thể tích của khối trụ có chiều cao \(h = a\) và bán kính đáy \(r = 2a\) bằng bao nhiêu?
Đáp án: C Phương pháp giải: Công thức tính thể tích của khối trụ có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \pi {R^2}h.\) Lời giải chi tiết: Ta có: \(V = \pi {r^2}h = \pi .{\left( {2a} \right)^2}.a = 4\pi {a^3}.\) Chọn C. Câu hỏi 26 : Một khối trụ có bán kính đáy bằng 5 và khoảng cách giữa hai đáy bằng 7. Thể tích khối trụ bằng :
Đáp án: C Phương pháp giải: Công thức tính thể tích của khối trụ có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \pi {R^2}h.\) Lời giải chi tiết: Theo đề bài ta có \(r = 5;\,\,\,h = 7\) \( \Rightarrow V = \pi {r^2}h = \pi {5^2}.7 = 175\pi \) Chọn C. Câu hỏi 27 : Cho hình trụ có thiết diện qua trục là một hình vuông, diện tích mỗi mặt đáy bằng \(9\pi \,\,\left( {c{m^2}} \right)\). Tính diện tích xung quanh của hình trụ đó.
Đáp án: B Phương pháp giải: Phương pháp: - Thiết diện qua trục của một hình trụ là một hình chữ nhật có 1 cạnh là đường cao, cạnh còn lại là đường kính đường tròn đáy của hình trụ. - Tính chiều cao \(h\) và bán kính đáy \(r\) của hình trụ đã cho. - Diện tích xung quành của hình trụ được tính bằng công thức: \({S_{xq}} = 2\pi rh\). Lời giải chi tiết: Cách giải: Thiết diện qua trục của hình trụ đã cho là một hình vuông nên chiều cao và đường kính đường tròn đáy của hình trụ bằng nhau. Diện tích mỗi mặt đáy của hình trụ bằng \(9\pi \left( {c{m^2}} \right)\) nên \(\pi {r^2} = 9\pi \Leftrightarrow r = 3\,\,\left( {cm} \right).\) Suy ra chiều cao của hình trụ đã cho là: \(h = 2r = 6\left( {cm} \right).\) Diện tích xung quanh của hình trụ đã cho là: \({S_{xq}} = 2\pi rh = 2.\pi .3.6 = 36\pi \left( {c{m^2}} \right)\). Chọn B. Câu hỏi 28 : Nếu một hình trụ có độ dài đường cao bằng \(2a,\) bán kính đường tròn đáy bằng \(a\) thì có diện tích xung quanh bằng
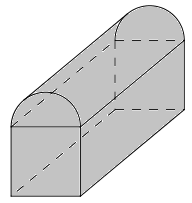
Đáp án: B Phương pháp giải: Công thức tính diện tích xung quanh hình trụ có bán kính đáy R, chiều cao h là: \({S_{xq}} = 2\pi Rh.\) Lời giải chi tiết: Ta có: \({S_{xq}} = 2\pi .a.2a = 4\pi {a^2}.\) Đáp án B. Câu hỏi 29 : Một hộp nữ trang được tạo thành từ một hình lập phương cạnh \(6cm\) và một nửa hình trụ có đường kính đáy bằng \(6cm\) (hình bên). Thể tích của hộp nữ trang này bằng:
Đáp án: C Phương pháp giải: Thể tích một nữ trang bằng tổng thể tích khối lập phương và nửa khối trụ. Lời giải chi tiết: + Thể tích khối lập phương cạnh 6 cm là \({V_1} = {6^3} = 216\,\,\left( {c{m^3}} \right)\). + Thể tích nửa khối trụ bán kính đáy r = 3cm, đường cao h = 6 cm là: \({V_2} = \dfrac{1}{2}.\left( {\pi {r^2}h} \right) = \dfrac{1}{2}\pi {.3^2}.6 = 27\pi \,\,\left( {c{m^3}} \right)\). Vậy thể tích một nữ trang là \(V = {V_1} + {V_2} = 216 + 27\pi \,\,\left( {c{m^3}} \right)\). Đáp án C. Câu hỏi 30 : Cho hình trụ bán kính \(5\,m,\) khoảng cách giữa hai đáy bằng \(7\,m.\) Cắt hình trụ bởi một mặt phẳng \(\left( P \right)\) song song với trục. Biết diện tích thiết diện bằng \(56\,{m^2}.\) Tính khoảng cách từ trục đến mặt phẳng \(\left( P \right).\)
Đáp án: B Phương pháp giải: Cho \(d//\left( \alpha \right),\,\,O \in d,\,\,\,H \in \left( \alpha \right)\) ta có: \(d\left( {d;\,\,\left( \alpha \right)} \right) = d\left( {O;\,\,\left( \alpha \right)} \right) = OH\) với \(OH \bot \left( \alpha \right).\) Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}OB = 5\,\,m\\OO' = BC = 7\,\,m\\{S_{ABCD}} = 56\,\,{m^2}\end{array} \right..\) \( \Rightarrow AB = \frac{{{S_{ABCD}}}}{{BC}}\frac{{56}}{7} = 8\,\,m.\) Gọi \(H\) là trung điểm của \(AB \Rightarrow \left\{ \begin{array}{l}AH = BH = 4\,\,m\\OH \bot AB = \left\{ H \right\}\end{array} \right..\) \( \Rightarrow OH \bot \left( {ABCD} \right).\) Lại có: \(OO'//\left( P \right) \equiv \left( {ABCD} \right)\) \( \Rightarrow d\left( {O;\,\,\,\left( {ABCD} \right)} \right) = OH.\) Áp dụng định lý Pitago ta có:\(OH = \sqrt {O{B^2} - B{H^2}} = \sqrt {{5^2} - {4^2}} = 3\,\,m.\) Chọn B. Câu hỏi 31 : Cho hình chữ nhật \(ABCD\) có \(AB = 2a\sqrt 3 ,\,\widehat {ADB} = 60^\circ .\) Gọi \(M,\,N\) lần lượt là trung điểm của \(AD,\,BC.\) Khối trụ tròn xoay tạo thành khi quay hình chữ nhật \(ABCD\) (kể cả điểm trong) xung quanh cạnh \(MN\) có thể tích bằng bao nhiêu ?
Đáp án: C Phương pháp giải: Thể tích khối trụ: \(V = \pi {r^2}h\) Lời giải chi tiết: Khi quay hình chữ nhật quanh \(MN\) ta được hình trụ bán kính \(MA\) và chiều cao \(MN = AB = AD\). Tam giác \(ABD\) có \(\widehat A = {90^0},AB = 2a\sqrt 3 \) nên \(AD = \dfrac{{AB}}{{\tan {{60}^0}}} = \dfrac{{2a\sqrt 3 }}{{\sqrt 3 }} = 2a\). Khi đó \(MA = \dfrac{1}{2}AD = a\). Vậy thể tích \(V = \pi M{A^2}.MN = \pi .{a^2}.2a\sqrt 3 = 2\pi {a^3}\sqrt 3 \). Chọn C Câu hỏi 32 : Cho \(ABCD\) là hình chữ nhật, \(AB = a,\,\,AD = b\). Quay hình chữ nhật \(ABCD\) xung quanh cạnh \(AB\) ta được một khối tròn xoay có thể tích bằng:
Đáp án: C Phương pháp giải: Quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta được hình trụ có chiều cao \(h = AB\) và bán kính đáy \(R = AD.\) Công thức tính thể tích của khối trụ có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \pi {R^2}h.\) Lời giải chi tiết: Quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta được hình trụ có chiều cao \(h = AB\) và bán kính đáy \(R = AD.\) \( \Rightarrow V = \pi .{b^2}a = \pi a{b^2}.\) Chọn C. Câu hỏi 33 : Một cái xúc xích dạng hình trụ có đường kính đáy 2cm và chiều cao 6cm, giả sử giá bán mỗi cm3 xúc xích là 500 đồng. Bạn An cần trả tiền để mua một gói 4 cái xúc xích. Số tiền gần đúng nhất cho 4 cái xúc xích là
Đáp án: C Phương pháp giải: - Tính thể tích của 1 cái xúc xích, sử dụng công thức tính thể tích khối trụ có chiều cao \(h\), bán kính đáy \(R\) là \(V = \pi {R^2}h\). - Tính giá bán 1 cái xúc xích. - Tính giá bán 4 cái xúc xích. Lời giải chi tiết: Thể tích của cái xúc xích là: \(V = \pi {R^2}h = \pi {\left( {\frac{2}{2}} \right)^2}.6 = 6\pi \,\,\left( {c{m^3}} \right)\). Giá bán 1 cái xúc xích là \(6\pi .500 = 3000\pi \) (đồng). Vậy giá bán 4 cái xúc xích là \(4.3000\pi = 12000\pi \approx 37999\) (đồng). Chọn C. Câu hỏi 34 : Một hình trụ có tỉ số giữa diện tích toàn phần và diện tích xung quanh bằng 3. Khẳng định nào sau đây là đúng?
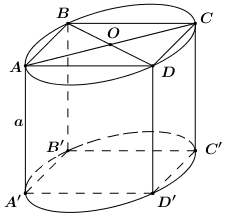
Đáp án: A Phương pháp giải: Công thức tính diện tích xung quanh hình trụ có bán kính đáy \(R,\;\) chiều cao \(h:\;\;{S_{xq}} = 2\pi Rh.\) Công thức tính diện tích toàn phần của hình trụ có bán kính đáy \(R,\;\) chiều cao \(h:\;\;{S_{tp}} = 2\pi Rh + 2\pi {R^2}.\) Lời giải chi tiết: Gọi bán kính và chiều cao của hình trụ đã cho lần lượt là \(R,\,\,h.\) Khi đó ta có: \(\begin{array}{l}\frac{{{S_{tp}}}}{{{S_{xq}}}} = 3 \Leftrightarrow \frac{{2\pi Rh + 2\pi {R^2}}}{{2\pi Rh}} = 3\\ \Leftrightarrow \pi Rh + \pi {R^2} = 3\pi Rh\\ \Leftrightarrow \pi {R^2} = 2\pi Rh\\ \Leftrightarrow R = 2h.\end{array}\) Chọn A. Câu hỏi 35 : Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Gọi \(\left( H \right)\) là hình trụ có hai đường tròn đáy lần lượt là đường tròn ngoại tiếp các hình vuông \(ABCD.A'B'C'D'\). Diện tích toàn phần của hình trụ \(\left( H \right)\) là:
Đáp án: D Phương pháp giải: Diện tích toàn phần của hình trụ có bán kính đáy \(R\), chiều cao \(h\) là: \({S_{tp}} = 2\pi R\left( {R + h} \right)\). Lời giải chi tiết: Gọi \(O = AC \cap BD\). Vì \(ABCD\) là hình vuông cạnh \(a \Rightarrow AC = a\sqrt 2 \). \( \Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\). Do đó hình trụ có bán kính đáy \(R = OA = \frac{{a\sqrt 2 }}{2}\), chiều cao \(h = AA' = a\). Diện tích toàn phần của hình trụ \(\left( H \right)\) là: \(\begin{array}{l}{S_{tp}} = 2\pi R\left( {h + R} \right) = 2\pi .\frac{{a\sqrt 2 }}{2}\left( {a + \frac{{a\sqrt 2 }}{2}} \right)\\\,\,\,\,\,\,\, = \frac{{\sqrt 2 \left( {2 + \sqrt 2 } \right)\pi {a^2}}}{2} = \left( {1 + \sqrt 2 } \right)\pi {a^2}\end{array}\) Chọn D. Câu hỏi 36 : Một hình trụ có diện tích xung quanh bằng \(S,\) diện tích đáy bằng diện tích một mặt cầu bán kính \(a,\) khi đó thể tích của hình trụ bằng :
Đáp án: A Phương pháp giải: Thể tích hình trụ \(V = \pi {R^2}h\), diện tích xung quanh \({S_{xq}} = 2\pi Rh\). Suy ra \(V = \dfrac{{{S_{xq}}.R}}{2}\). Lời giải chi tiết: Diện tích đáy \({S_d} = 4\pi {a^2} \Rightarrow \pi {R^2} = 4\pi {a^2} \Leftrightarrow R = 2a\). Do đó \(V = \dfrac{{{S_{xq}}.R}}{2} = \dfrac{{S.2a}}{2} = Sa\). Chọn A. Câu hỏi 37 : Một hình trụ \(\left( T \right)\) có bán kính đáy \(R\) và có thiết diện qua trục là hình vuông. Tính diện tích xung quanh \({S_{xq}}\) của khối trụ.
Đáp án: D Phương pháp giải: - Tìm mối quan hệ của \(h\) theo \(R\). - Áp dụng công thức tính diện tích xung quanh. Lời giải chi tiết: Ta có thiết diện qua trục của hình trụ là hình vuông nên \(h = 2R\). Vậy diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi Rh = 4\pi {R^2}.\) Chọn D. Câu hỏi 38 : Một hình trụ có diện tích xung quanh bằng \(4\pi \) và có thiết diện qua trục của nó là một hình vuông. Tính thể tích của khối trụ
Đáp án: B Phương pháp giải: Diện tích xung quanh của khối trụ là \(2\pi rh\) (\(r\)là bán kính đáy, \(h\) là chiều cao của khối trụ). Thể tich của khối trụ là \(\pi {r^2}h.\) Lời giải chi tiết: Thiết diện qua trục của khối trụ là hình vuông nên chiều cao của khối trụ bằng đường kính đáy. \( \Rightarrow h = 2r\) Diện tích xung quanh bằng \(4\pi \Rightarrow 2\pi rh = 4\pi \) \( \Rightarrow 2\pi .r.2r = 4\pi \Leftrightarrow {r^2} = 1 \Leftrightarrow r = 1 \Rightarrow h = 2\). Vậy thể tích của khối trụ là \(V = \pi {r^2}h = \pi {.1^2}.2 = 2\pi .\) Chọn B. Câu hỏi 39 : Cắt một hình trụ bằng một mặt phẳng qua trục của nó, ta được thiết diện là một hình vuông cạnh 2a. Diện tích xung quanh của hình trụ bằng
Đáp án: B Phương pháp giải: Diện tích xung quanh của hình trụ có bán kính đáy \(R\), chiều cao \(h\) là \({S_{xq}} = 2\pi Rh\). Lời giải chi tiết: Vì thiết diện qua trục là hình vuông nên ta có \(R = a,\,\,h = 2a\). Vậy diện tích xung quanh của hình trụ là: \({S_{xq}} = 2\pi Rh = 2\pi .a.2a = 4\pi {a^2}.\) Chọn B Câu hỏi 40 : Một hình trụ có diện tích xung quanh bằng \(4\pi {a^2}\)và độ dài đường cao bằng 2a. Tính bán kính đáy của hình trụ đó
Đáp án: C Phương pháp giải: Áp dụng công thức tính diện tích xung quanh của hình trụ: \({S_{xq}} = 2\pi Rh\) trong đó \(R,\,\,h\) lần lượt là bán kính đáy và chiều cao của hình trụ. Lời giải chi tiết: Ta có: \({S_{xq}} = 2\pi Rh = 4\pi {a^2} \Leftrightarrow 2\pi .R.2a \Leftrightarrow R = a.\) Chọn C
|