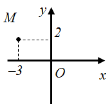40 bài tập trắc nghiệm hệ trục tọa độ mức độ nhận biết, thông hiểuLàm bàiCâu hỏi 1 : Trong mặt phẳng Oxy cho A(2;-3); B(4;7) tọa độ trung điểm I của đoạn thẳng AB là:
Đáp án: C Lời giải chi tiết: Gọi Ta có: $$\left\{ \matrix{ {x_I} = {{{x_A} + {x_B}} \over 2} \hfill \cr {y_I} = {{{y_A} + {y_B}} \over 2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ {x_I} = {{2 + 4} \over 2} = 3 \hfill \cr {y_I} = {{ - 3 + 7} \over 2} = 2 \hfill \cr} \right. \Rightarrow I\left( {3;2} \right)$$ Câu hỏi 2 : Cho tam giác \(ABC\) có \(A\left( {3;1} \right),\,\,B\left( {1; - 3} \right)\), đỉnh \(C\) nằm trên \(Oy\) và trọng tâm \(G\) nằm trên trục \(Ox\). Tìm tọa độ đỉnh \(C.\)
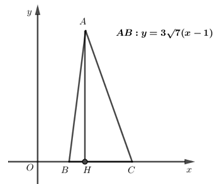
Đáp án: A Phương pháp giải: \(G({x_G};{y_G})\)là trọng tâm tam giác ABC: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\) Lời giải chi tiết: Theo đề bài ta có: \(C \in Oy;\,\,G \in O\,x \Rightarrow C\left( {0;{y_C}} \right),\,\,G\left( {{x_G};0} \right)\) \(G\) là trọng tâm tam giác \( \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{x_A} + {x_B} + {x_C} = 3{x_G}}\\{{y_A} + {y_B} + {y_C} = 3{y_G}}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}3 + 1 + 0 = 3{x_G}\\1 - 3 + {y_C} = 0\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_G} = \frac{4}{3}}\\{{y_C} = 2}\end{array}} \right. \Rightarrow \left\{ \begin{array}{l}G\left( {\frac{4}{3};\,\,0} \right)\\C\left( {0;\,\,2} \right)\end{array} \right..\) Vậy \(C\left( {0;2} \right).\) Chọn A. Câu hỏi 3 : Trong mặt phẳng với hệ toạ độ \(Oxy,\) cho \(\Delta ABC\) cân có đáy \(BC.\) Đỉnh \(A\) có toạ độ là các số dương, hai điểm \(B\) và \(C\) nằm trên trục \(Ox,\) phương trình cạnh \(AB\) là \(y = 3\sqrt 7 \left( {x - 1} \right).\) Biết chu vi tam giác \(ABC\) bằng \(18,\) tìm toạ độ các đỉnh \(A,\, B, \,C.\)
Đáp án: C Phương pháp giải: Sử dụng tính chất của tam giác cân và công thức tính chu vi tam giác để làm bài. Lời giải chi tiết:
Theo đề bài ta có: \(\begin{array}{l}\left\{ B \right\} = AB \cap Ox \Rightarrow B\left( {1;\,\,0} \right)\\A \in AB \Rightarrow A\left( {a;\,\,\,3\sqrt 7 \left( {a - 1} \right)} \right) \Rightarrow a > 1\,\,\,\,\left( {do{\rm{ }}{x_A} > 0,{y_A} > 0} \right)\end{array}\) Gọi \(AH\) là đường cao của \(\Delta ABC \Rightarrow H\) là hình chiếu của \(A\) trên \(Ox\) \( \Rightarrow H\left( {a;\,\,0} \right)\) Mà \(\Delta ABC\) là \(\Delta \) cân tại \(A \Rightarrow H\) là trung điểm của \(BC\) \(\begin{array}{l} \Rightarrow C\left( {2a - 1;0} \right) \Rightarrow \left\{ \begin{array}{l}\overrightarrow {BC} = \left( {2a - 2;\,\,0} \right)\\\overrightarrow {AB} = \left( {1 - a;\,\, - 3\sqrt 7 \left( {a - 1} \right)} \right)\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}BC = \sqrt {{{\left[ {2\left( {a - 1} \right)} \right]}^2}} = 2\left( {a - 1} \right)\,\,\,\,\left( {a > 1} \right)\\AC = AB = \sqrt {{{\left( {1 - a} \right)}^2} + 63\left( {a - 1} \right)} = 8\left( {a - 1} \right)\,\,\,\,\left( {a > 1} \right)\end{array} \right.\end{array}\) Chu vi \(\Delta ABC\) là \(18 \Rightarrow AB + BC + CA = 18\) \(\begin{array}{l}\, \Leftrightarrow \,2.8\left( {a - 1} \right) + 2\left( {a - 1} \right) = 18\\ \Leftrightarrow 18\left( {a - 1} \right) = 18\\ \Leftrightarrow a - 1 = 1\\ \Leftrightarrow a = 2\\ \Rightarrow \left\{ \begin{array}{l}C\left( {3;\,\,0} \right)\\A\left( {2;\,\,3\sqrt 7 } \right)\end{array} \right..\end{array}\) Chọn C Câu hỏi 4 : Cho hình bình hành \(ABCD\) có toạ độ tâm \(I\left( {3;2} \right)\) và hai đỉnh \(B\left( { - 1;3} \right);C\left( {8; - 1} \right).\) Tìm toạ độ hai đỉnh \(A,D.\)
Đáp án: C Phương pháp giải: \(I\left( {{x_I};{y_I}} \right)\) là trung điểm của cạnh \(AB\) với \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\) thì \(\left\{ {\begin{array}{*{20}{c}}{{x_I} = \frac{{{x_A} + {x_B}}}{2}}\\{{y_I} = \frac{{{y_A} + {y_B}}}{2}}\end{array}} \right.\) Lời giải chi tiết: \(I\) là trung điểm của \(BD \Rightarrow D = \left( {2{x_I} - {x_B};2{y_I} - {y_B}} \right) \Rightarrow D\left( {7;1} \right)\) \(I\) là trung điểm của \(AC \Rightarrow A = \left( {2{x_I} - {x_C};2{y_I} - {y_C}} \right) \Rightarrow A\left( { - 2;5} \right)\) Chọn C. Câu hỏi 5 : Trong hệ trục tọa độ \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\), cho vectơ \(\overrightarrow u = 3\overrightarrow j - 4\overrightarrow i \). Tọa độ của vectơ \(\overrightarrow u \) là
Đáp án: B Phương pháp giải: Trong hệ trục tọa độ \(\left( {O;\overrightarrow i ,\overrightarrow j } \right)\), vectơ \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \) có tọa độ \(\overrightarrow u = (a;b)\) Lời giải chi tiết: Ta có: \(\overrightarrow u = - 4\overrightarrow i + 3\overrightarrow j \Rightarrow \overrightarrow u = \left( { - 4;\,\,3} \right).\) Chọn B. Câu hỏi 6 : Trong mặt phẳng tọa độ \({\rm{Oxy}}\) cho tam giác \({\rm{ABC}}\) có trọng tâm \(G\left( {1;\,\,2} \right).\) Biết \(A\left( {2;\,\,2} \right)\,\,,\,B\left( {0; - 1} \right),\) tìm tọa độ điểm \(C:\)
Đáp án: D Phương pháp giải: Sử dụng công thức trọng tâm \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right..\) Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 = \frac{{2 + 0 + {x_C}}}{3}\\2 = \frac{{2 + \left( { - 1} \right) + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 1\\{y_C} = 5\end{array} \right. \Rightarrow C\left( {1;\,\,5} \right).\) Chọn D. Câu hỏi 7 : Trong mặt phẳng tọa độ \(Oxy\), cho tam giác ABC có \(A(2;\,\,1),\,B\left( {4;\,\, - 3} \right),\,C\left( {3;\,\,5} \right)\). Tìm tọa độ trọng tâm G của tam giác ABC.
Đáp án: B Phương pháp giải: Sử dụng công thức về tọa độ trọng tâm của tam giác. Lời giải chi tiết: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{2 + 4 + 3}}{3} = 3\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{1 - 3 + 5}}{3} = 1\end{array} \right. \Rightarrow G\left( {3;1} \right).\) Chọn B. Câu hỏi 8 : Trong mặt phẳng \(Oxy\), cho hai điểm \(A\left( { - 1;2} \right),B\left( {1; - 3} \right)\). Tìm tọa độ điểm \(D\) sao cho B là trung điểm của AD.
Đáp án: A Phương pháp giải: Áp dụng công thức tọa độ trung điểm. Lời giải chi tiết: Gọi \(D\left( {{x_D};{y_D}} \right)\). Vì \(B\) là trung điểm của \(AD \Rightarrow \left\{ \begin{array}{l}\,\,\,\,1\, = \frac{{ - 1 + {x_D}}}{2}\\ - 3 = \frac{{2 + {y_D}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} - 1 = 2\\{y_D} + 2 = - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 3\\{y_D} = - 8\end{array} \right. \Rightarrow D\left( {3; - 8} \right).\) Chọn A. Câu hỏi 9 : Trong mặt phẳng \(Oxy\), cho \(M\left( { - 1;5} \right)\) và \(N\left( {2;4} \right).\) Tọa độ của vectơ \(\overrightarrow {MN} \) là:
Đáp án: A Phương pháp giải: Cho hai điểm \(A\left( {{x_A};\,\,{y_A}} \right)\) và \(B\left( {{x_B};\,\,{y_B}} \right) \Rightarrow \overrightarrow {AB} = \left( {{x_B} - {x_A};\,\,{y_B} - {y_A}} \right).\) Lời giải chi tiết: Ta có: \(M\left( { - 1;\,\,5} \right),N\left( {2;\,\,4} \right) \Rightarrow \overrightarrow {MN} = \left( {3; - 1} \right).\) Chọn A. Câu hỏi 10 : Trong mặt phẳng \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\) cho các vectơ \(\overrightarrow u \left( { - 2;3} \right)\) và \(\overrightarrow v \left( {6;1} \right).\) Khi đó vectơ \(\overrightarrow x = 2\overrightarrow u - 3\overrightarrow v + \overrightarrow j \) có tọa độ bằng:
Đáp án: A Phương pháp giải: Sử dụng công thức cộng, trừ vectơ theo tọa độ. Lời giải chi tiết: \(\begin{array}{l}\overrightarrow x = 2\overrightarrow u - 3\overrightarrow v + \overrightarrow j = 2\left( { - 2\overrightarrow i + 3\overrightarrow j } \right) - 3\left( {6\overrightarrow i + \overrightarrow j } \right) + \overrightarrow j = - 22\overrightarrow i + 4\overrightarrow j .\\ \Rightarrow \overrightarrow x = \left( { - 22;\,\,4} \right).\end{array}\) Chọn A. Câu hỏi 11 : Trong mặt phẳng tọa độ \(Oxy\), cho hình bình hành \(ABCD.\) Biết \(A\left( {1;3} \right),B\left( { - 3;1} \right),C\left( { - 2;2} \right).\) Tọa độ điểm \(D\) là:
Đáp án: C Phương pháp giải: Dùng tính chất hình bình hành. Lời giải chi tiết: Gọi \(D\left( {a;b} \right).\) Do \(ABCD\) là hình bình hành \( \Rightarrow \overrightarrow {AB} = \overrightarrow {DC} .\) Mà \(\overrightarrow {AB} = \left( { - 4; - 2} \right),\,\,\,\overrightarrow {DC} = \left( { - 2 - a;\,\,\,2 - b} \right) \Rightarrow \left\{ \begin{array}{l} - 4 = - 2 - a\\ - 2 = 2 - b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 2\\b = 4\end{array} \right..\) Chọn C. Câu hỏi 12 : Trong hệ trục \(Oxy\), cho hai điểm \(A\left( {2;3} \right),\,\,B\left( { - 1;4} \right).\) Với \(M\) bất kì, tìm tọa độ \(\overrightarrow {MA} - \overrightarrow {MB} ?\)
Đáp án: B Phương pháp giải: Sử dụng công thức tọa độ của vectơ. Lời giải chi tiết: Ta có: \(\overrightarrow {MA} - \overrightarrow {MB} = \overrightarrow {BA} = \left( {3; - 1} \right).\) Chọn B. Câu hỏi 13 : Trong hệ trục \(Oxy\), cho điểm \(G\left( {1; - 2} \right).\) Tìm tọa độ điểm \(A \in Ox,B \in Oy\) sao cho \(G\) là trọng tâm tam giác \(OAB.\)
Đáp án: B Phương pháp giải: Sử dụng công thức tọa độ trọng tâm của tam giác. Lời giải chi tiết: Ta có:\(A \in Ox \Rightarrow A\left( {a;\,\,0} \right);\,\,B \in Oy \Rightarrow B\left( {0;\,\,b} \right).\) Vì \(G\) là trọng tâm tam giác \(OAB\) \( \Rightarrow \left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_O}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_O}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 = \frac{{a + 0 + 0}}{3}\\ - 2 = \frac{{0 + b + 0}}{3}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 3\\b = - 6\end{array} \right. \Rightarrow G\left( {3; - 6} \right).\) Chọn B. Câu hỏi 14 : Trong mặt phẳng tọa độ \(Oxy\) cho tam giác \(ABC\) có \(A\left( { - 4;7} \right),\,B\left( {a;b} \right),\,C\left( { - 1; - 3} \right).\) Tam giác \(ABC\) nhận \(G\left( { - 1;3} \right)\) làm trọng tâm. Tính \(T = 2a + b.\)
Đáp án: A Phương pháp giải: Điểm \(G\) là trọng tâm tam giác \(ABC\) thì \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right.\) Lời giải chi tiết: Điểm \(G\) là trọng tâm tam giác \(ABC\) thì \(\left\{ \begin{array}{l} - 1 = \frac{{ - 4 + a - 1}}{3}\\3 = \frac{{7 + b - 3}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 5 + a = - 3\\4 + b = 9\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 5\end{array} \right.\) \( \Rightarrow T = 2a + b = 2.2 + 5 = 9\) Chọn A. Câu hỏi 15 : Cho \(\overrightarrow u = \left( {2; - 2} \right),\,\,\overrightarrow v = \left( {1;8} \right)\). Khẳng định nào sau đây là đúng ?
Đáp án: A Phương pháp giải: Cho véc tơ \(\overrightarrow u = \left( {a;b} \right)\), khi đó \(\overrightarrow v = k\overrightarrow u \,\left( {k \ne 0} \right)\) cùng hướng với \(\overrightarrow u \Leftrightarrow k > 0\) và ngược hướng với \(\overrightarrow u \Leftrightarrow k < 0.\) Lời giải chi tiết: Ta có: \(\overrightarrow u + \overrightarrow v = \left( {2 + 1; - 2 + 8} \right) = \left( {3;6} \right) = 3\left( {1;2} \right) = 3\overrightarrow u \) Nên \(\overrightarrow u + \overrightarrow v \) và \(\overrightarrow u \) cùng hướng, do đó A đúng. Chọn A Câu hỏi 16 : Cho \(3\) điểm \(A\left( {1;4} \right);\,\,B\left( {3;2} \right)\,;\,\,C\left( {5;4} \right)\). Chu vi tam giác \(ABC\) bằng bao nhiêu ?
Đáp án: B Phương pháp giải: Chu vi tam giác bằng tổng ba cạnh. Cho \(A\left( {{x_1};{y_1}} \right);\,B\left( {{x_2};{y_2}} \right) \Rightarrow AB = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \) Lời giải chi tiết: Ta có: \(\begin{array}{l}AB = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( {2 - 4} \right)}^2}} = 2\sqrt 2 \\AC = \sqrt {{{\left( {5 - 1} \right)}^2} + {{\left( {4 - 4} \right)}^2}} = 4\\BC = \sqrt {{{\left( {5 - 3} \right)}^2} + {{\left( {4 - 2} \right)}^2}} = 2\sqrt 2 \end{array}\) Chu vi tam giác \(ABC\) bằng \(AB + BC + AC = 4 + 4\sqrt 2 .\) Chọn B Câu hỏi 17 : Cho tam giác \(ABC\) có \(A\left( {1;3} \right),\,\,B\left( {9;7} \right),\,\,C\left( {11; - 1} \right),\,\,M\) và \(N\) lần lượt là trung điểm của \(AB\) và \(AC.\) Tọa độ của \(\overrightarrow {MN} \) là :
Đáp án: B Phương pháp giải: Sử dụng tính chất đường trung bình: \(MN\) là đường trung bình của tam giác \(ABC\) thì \(\overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} \). Lời giải chi tiết: Do \(M,N\) là trung điểm của \(AB,AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\). \( \Rightarrow \overrightarrow {MN} = \frac{1}{2}\overrightarrow {BC} \). Mà \(\overrightarrow {BC} = \left( {2; - 8} \right)\) nên \(\overrightarrow {MN} = \frac{1}{2}\left( {2; - 8} \right) = \left( {1; - 4} \right)\). Chọn B. Câu hỏi 18 : Trong mặt phẳng tọa độ \(Oxy\), cho \(A\left( { - 1;2} \right)\) và \(B\left( {3; - 1} \right)\). Tọa độ của vectơ \(\overrightarrow {BA} \) là
Đáp án: D Phương pháp giải: Tọa độ véc tơ \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A}} \right)\) Lời giải chi tiết: \(A\left( { - 1;2} \right)\) và \(B\left( {3; - 1} \right)\)\( \Rightarrow \overrightarrow {BA} = \left( { - 1 - 3;2 + 1} \right) = \left( { - 4;3} \right)\). Chọn D. Câu hỏi 19 : Cho \(\overrightarrow a = \left( {2;1} \right),\overrightarrow b = \left( {3;4} \right),\overrightarrow c = \left( { - 7;2} \right).\) Tìm vectơ \(\overrightarrow p \) sao cho : \(4\overrightarrow p - 2\overrightarrow a = \overrightarrow b - 3\overrightarrow c \)
Đáp án: B Phương pháp giải: Sử dụng công thức \(k\overrightarrow a \pm l\overrightarrow b = \left( {k{x_1} \pm l{x_2};k{y_1} \pm l{y_2}} \right)\). Lời giải chi tiết: \(\begin{array}{l}4\overrightarrow p - 2\overrightarrow a = \overrightarrow b - 3\overrightarrow c \Leftrightarrow \overrightarrow p = \frac{1}{4}\left( {2\overrightarrow a + \overrightarrow b - 3\overrightarrow c } \right)\\ \Leftrightarrow \overrightarrow p = \frac{1}{4}\left( {2.2 + 3 - 3.\left( { - 7} \right);2.1 + 4 - 3.2} \right)\\ \Leftrightarrow \overrightarrow p = \frac{1}{4}\left( {28;0} \right) = \left( {7;0} \right).\end{array}\) Vậy \(\overrightarrow p = \left( {7;0} \right)\). Chọn B. Câu hỏi 20 : Trong mặt phẳng với hệ trục tọa độ \(Oxy\) cho điểm \(M\) như hình vẽ bên. Khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: Dựa vào đồ thị hàm số để suy ra tọa độ điểm \(M\) và từ đó tính tọa độ vecto \(\overrightarrow {OM} .\) Lời giải chi tiết: Ta có: \(M\left( { - 3;2} \right) \Rightarrow \overrightarrow {OM} = \left( { - 3;2} \right).\) Chọn C. Câu hỏi 21 : Vectơ nào sau đây cùng hướng với vectơ \(\overrightarrow a = \left( {2;3} \right)?\)
Đáp án: C Phương pháp giải: \(\overrightarrow a ,\overrightarrow b \) cùng hướng \( \Leftrightarrow \overrightarrow a = k\overrightarrow b \,\,\,\,\left( {k > 0} \right).\) Lời giải chi tiết: Ta có: \(\overrightarrow b = \left( {4;6} \right) = 2\left( {2;3} \right) = 2\overrightarrow a .\) Chọn C. Câu hỏi 22 : Trong mặt phẳng \(Oxy,\) cho tam giác \(EHF\) có \(E\left( { - 1;\,\,3} \right),H\left( {3; - 4} \right),F\left( {4;\,\,2} \right).\) Tìm tọa độ trọng tâm \(G\) của tam giác \(EHF.\)
Đáp án: D Phương pháp giải: Công thức tọa độ trọng tâm của tam giác. Lời giải chi tiết: Ta có:\(G\left( {{x_G};\,\,{y_G}} \right)\) là trọng tâm tam giác \(EHF\)\( \Rightarrow \left\{ \begin{array}{l}{x_G} = \frac{{ - 1 + 3 + 4}}{3} = 2\\{y_G} = \frac{{3 - 4 + 2}}{3} = \frac{1}{3}\end{array} \right..\) Chọn D. Câu hỏi 23 : Cho ba vectơ \(\overrightarrow a = \left( {2; - 2} \right),\overrightarrow b = \left( {1;4} \right),\overrightarrow c = \left( {5;2} \right).\) Biết \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b .\) Tính \(S = {m^2} + n.\)
Đáp án: B Phương pháp giải: Áp dụng công thức: \(\overrightarrow a = \left( {m;\,\,n} \right) \Rightarrow k\overrightarrow a = \left( {km;\,\,kn} \right).\) Lời giải chi tiết: Ta có: \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \Rightarrow \left\{ \begin{array}{l}5 = m.2 + n.1\\2 = m.\left( { - 2} \right) + n.4\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m = \frac{9}{5}\\n = \frac{7}{5}\end{array} \right. \Rightarrow {m^2} + n = \frac{{116}}{{25}}.\) Chọn B. Câu hỏi 24 : Trong mặt phẳng tọa độ \(Oxy,\) cho điểm \(B\left( { - 1;3} \right),D\left( {7; - 1} \right).\) Tìm tọa độ trung điểm \(I\) của đoạn \(BD.\)
Đáp án: B Phương pháp giải: Công thức tọa độ trung điểm. Lời giải chi tiết: Ta có: \(I\left( {{x_I};\,\,{y_I}} \right)\) là trung điểm của \(BD\) \( \Rightarrow \left\{ \begin{array}{l}{x_I} = \frac{{ - 1 + 7}}{2} = 3\\{y_I} = \frac{{3 - 1}}{2} = 1\end{array} \right. \Rightarrow I\left( {3;1} \right).\) Chọn B. Câu hỏi 25 : Trong mặt phẳng tọa độ \(Oxy,\) cho các điểm \(A\left( {1;4} \right),\,\,B\left( { - 3;2} \right),\,\,C\left( { - 3; - 5} \right),\,\,M\left( {{x_M};{y_M}} \right)\) thỏa \(\overrightarrow {MA} + \overrightarrow {MB} - 2\overrightarrow {AC} = \overrightarrow 0 ,\) khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: Sử dụng công thức trung điểm. Lời giải chi tiết: Gọi \(I\) là trung điểm \(AB.\) \(\begin{array}{l}A\left( {1;\,\,4} \right),\,\,\,B\left( { - 3;2} \right),\,\,\,C\left( { - 3; - 5} \right),\,\,\,M\left( {{x_M};{y_M}} \right)\\ \Rightarrow I\left( { - 1;\,\,3} \right)\\ \Rightarrow \left\{ \begin{array}{l}\overrightarrow {MI} = \left( { - 1 - {x_M};3 - {y_M}} \right)\\\overrightarrow {AC} = \left( { - 4; - 9} \right)\end{array} \right..\end{array}\) \(\overrightarrow {MA} + \overrightarrow {MB} - 2\overrightarrow {AC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {MI} = \overrightarrow {AC} \)\( \Leftrightarrow \left\{ \begin{array}{l} - 1 - {x_M} = - 4\\3 - {y_M} = - 9\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 3\\{y_M} = 12\end{array} \right..\) Chọn C. Câu hỏi 26 : Trong mặt phẳng tọa độ \(Oxy,\) cho hai điểm \(M\left( {2; - 3} \right),N\left( { - 1;2} \right)\). Tìm tọa độ điểm \(E\) thuộc trục hoành, điểm \(F\) thuộc trục tung sao cho tứ giác \(MNEF\) là hình bình hành.
Đáp án: C Phương pháp giải: Sử dụng tính chất của hình bình hành. Lời giải chi tiết: Gọi \(E\left( {a;0} \right),\,\,\,F\left( {0;b} \right).\) Vì \(MNEF\) là hình bình hành suy ra \(\overrightarrow {MN} = \overrightarrow {FE} \)\( \Rightarrow \left\{ \begin{array}{l} - 3 = a\\5 = - b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 3\\b = 5\end{array} \right..\) Chọn C. Câu hỏi 27 : Trong mặt phẳng tọa độ Oxy, cho hình bình hành ABCD với A(2;– 2), B(3; 4), C(– 1; 5). Khi đó điểm D có tọa độ là:
Đáp án: C Phương pháp giải: Tứ giác ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}{x_B} - {x_A} = {x_C} - {x_D}\\{y_B} - {y_A} = {y_C} - {y_D}\end{array} \right..\) Lời giải chi tiết: Gọi D(a; b). Khi đó ta có: ABCD là hình bình hành \( \Leftrightarrow \overrightarrow {AB} = \overrightarrow {DC} \) \(\begin{array}{l} \Leftrightarrow \left( {1;\,\,6} \right) = \left( { - 1 - a;\,\,5 - b} \right)\\ \Leftrightarrow \left\{ \begin{array}{l} - 1 - a = 1\\5 - b = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 2\\b = - 1\end{array} \right. \Rightarrow D\left( { - 2; - 1} \right).\end{array}\) Đáp án C. Câu hỏi 28 : Cho \(\overrightarrow u \)= (1;-2) và \(\overrightarrow v \) = (-2;2). Khi đó \(2\overrightarrow u + \overrightarrow v \) bằng:
Đáp án: C Phương pháp giải: Sử dụng các công thức cộng vectơ và nhân véctơ với 1 số. \(\begin{array}{l}\overrightarrow a = \left( {{x_1};{y_1}} \right);\,\,\overrightarrow b = \left( {{x_2};{y_2}} \right)\\ \Rightarrow k\overrightarrow a = \left( {k{x_1};k{y_1}} \right)\\\,\,\,\,\,\,\,\overrightarrow a + \overrightarrow b = \left( {{x_1} + {x_2};{y_1} + {y_2}} \right)\end{array}\) Lời giải chi tiết: Ta có \(\begin{array}{l}2\overrightarrow u = \left( {2; - 4} \right)\\\,\,\,\overrightarrow v = \left( { - 2;2} \right)\\ \Rightarrow 2\overrightarrow u + \overrightarrow v = \left( {0; - 2} \right)\end{array}\) Đáp án C. Câu hỏi 29 : Trong măt phẳng với hệ trục tọa độ \(\left( {O;\overrightarrow i ;\overrightarrow j } \right)\) cho các vectơ \(\overrightarrow u = 2\overrightarrow i - 3\overrightarrow j \) và \(\overrightarrow v = k\overrightarrow i + \frac{1}{3}\overrightarrow j \). Biết \(\overrightarrow u \bot \overrightarrow v \), khid đó k bằng:
Đáp án: C Phương pháp giải: - Xác định tọa độ các vectơ \(\overrightarrow u ,\,\,\overrightarrow v \) như sau: \(\overrightarrow u = x\overrightarrow i + y\overrightarrow j \) \( \Rightarrow \overrightarrow u \left( {x;y} \right)\). - \(\overrightarrow u \bot \overrightarrow v \Leftrightarrow \overrightarrow u .\overrightarrow v = 0\). Lời giải chi tiết: Ta có: \(\overrightarrow u = 2\overrightarrow i - 3\overrightarrow j \Rightarrow \overrightarrow u \left( {2; - 3} \right)\) và \(\overrightarrow v = k\overrightarrow i + \frac{1}{3}\overrightarrow j \Rightarrow \overrightarrow v \left( {k;\frac{1}{3}} \right)\). Vì \(\overrightarrow u \bot \overrightarrow v \) nên \(\overrightarrow u .\overrightarrow v = 0\) \(\begin{array}{l} \Leftrightarrow 2k - 3.\frac{1}{3} = 0\\ \Leftrightarrow 2k - 1 = 0\\ \Leftrightarrow k = \frac{1}{2}\end{array}\) Đáp án C. Câu hỏi 30 : Trong mặt phẳng với hệ trục tọa độ \(\left( {O;\,\,\overrightarrow i ;\,\,\overrightarrow j } \right)\) cho điểm M thỏa mãn \(\overrightarrow {OM} = - 2\overrightarrow i + 3\overrightarrow j .\) Tọa độ của M là:
Đáp án: C Phương pháp giải: Cho vetco \(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \Rightarrow \overrightarrow u = \left( {a;\,\,b} \right).\) Lời giải chi tiết: Ta có: \(\overrightarrow {OM} = - 2\overrightarrow i + 3\overrightarrow j \Rightarrow \overrightarrow {OM} = \left( { - 2;\,\,3} \right) \Rightarrow M\left( { - 2;\,\,3} \right).\) Đáp án C. Câu hỏi 31 : Trong mặt phẳng tọa độ Oxy có hai vectơ đơn vị trên hai trục là \(\overrightarrow i ;\overrightarrow j \). Cho \(\overrightarrow v = a.\overrightarrow i + b.\overrightarrow j \), nếu \(\overrightarrow v .\overrightarrow j = 3\) thì (a;b) có thể là cặp số nào sau đây?
Đáp án: A Phương pháp giải: - Với \(\overrightarrow i ,\overrightarrow j \) là các vector đơn vị ta có \(\overrightarrow i .\overrightarrow j = 0\,\,;\,\,{\overrightarrow i ^2} = {\overrightarrow j ^2} = 1.\) - Sử dụng công thức tính tích vô hướng hai vector theo tọa độ. Lời giải chi tiết: Vì \(\overrightarrow v = a.\overrightarrow i + b.\overrightarrow j \) nên \(\overrightarrow v .\overrightarrow j = 3 \Leftrightarrow (a.\overrightarrow i + b.\overrightarrow j ).\overrightarrow j = 3 \Leftrightarrow a.\overrightarrow i .\overrightarrow j + b.\overrightarrow j .\overrightarrow j = 3 \Leftrightarrow b.{\overrightarrow j ^2} = 3 \Leftrightarrow b = 3\) (vì \(\overrightarrow i \bot \overrightarrow j \) nên \(\overrightarrow i .\overrightarrow j = 0\)) Chọn A. Câu hỏi 32 : Cho hai điểm \(A\left( {1;2} \right),B\left( {9; - 4} \right)\). Độ dài đoạn thẳng AB bằng:
Đáp án: D Phương pháp giải: Tính độ dài đoạn thẳng khi biết tọa độ 2 điểm đầu mút \(AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} \) Lời giải chi tiết: Ta có: \(AB = \sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} = \sqrt {{{\left( {1 - 9} \right)}^2} + {{\left( {2 + 4} \right)}^2}} = 10.\) Chọn D. Câu hỏi 33 : \(A\left( {1;1} \right);\,\,B\left( {2;6} \right).\) Tìm M thuộc đoạn AB để \(MA = 2MB\).
Đáp án: A Phương pháp giải: Lời giải chi tiết: Giả sử \(\begin{array}{l}M\left( {a;b} \right).\,\,MA = 2MB \Rightarrow \overrightarrow {MA} = - 2\overrightarrow {MB} \\ \Leftrightarrow \left( {1 - a;1 - b} \right) = - 2\left( {2 - a;6 - b} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}1 - a = - 4 + 2a\\1 - b = - 12 + 2b\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = \frac{5}{3}\\b = \frac{{13}}{3}\end{array} \right. \Rightarrow M\left( {\frac{5}{3};\frac{{13}}{3}} \right)\end{array}\) Chọn A. Câu hỏi 34 : \(A\left( {1;1} \right);\,\,B\left( {2;5} \right);\,\,C\left( {4;1} \right)\). Tìm M để \(2\overrightarrow {MA} + 3\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)
Đáp án: D Phương pháp giải: Lời giải chi tiết: Cách 1: Tự luận Giả sử \(M\left( {x;y} \right)\) thỏa mãn \(2\overrightarrow {MA} + 3\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \) \(\begin{array}{l} \Leftrightarrow 2\left( {1 - x;1 - y} \right) + 3\left( {2 - x;5 - y} \right) + \left( {4 - x;1 - y} \right) = \left( {0;0} \right)\\ \Leftrightarrow \left\{ \begin{array}{l} - 6x + 12 = 0\\ - 6y + 18 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 3\end{array} \right. \Rightarrow M\left( {2;3} \right)\end{array}\) Cách 2: Trắc nghiệm \[\begin{array}{*{20}{c}}{}&{\left( {2;2} \right)}\\ + &{\left( {6;15} \right)}\\{}&{\left( {4;1} \right)}\\\hline{}&{\left( {12;18} \right):6}\end{array}\] \( \Rightarrow M\left( {2;3} \right)\) Chọn D. Câu hỏi 35 : \(A\left( {1;2} \right);\,\,B\left( { - 1;5} \right);\,\,C\left( {2;m} \right)\). Tìm m để \(C \in AB\).
Đáp án: B Phương pháp giải: Lời giải chi tiết: \(\overrightarrow {AC} = \left( {1;m - 2} \right);\,\,\overrightarrow {AB} = \left( { - 2;3} \right)\) Để \(C \in AB\) thì \(\overrightarrow {AC} //\overrightarrow {AB} \Rightarrow \frac{1}{{ - 2}} = \frac{{m - 2}}{3} \Rightarrow m = \frac{1}{2}\) Chọn B. Câu hỏi 36 : Trong mặt phẳng tọa độ Oxy cho hai điểm \(A\left( { - 3;2} \right);\,\,B\left( {1;5} \right)\). Khoảng cách giữa hai điểm A và B bằng bao nhiêu?
Đáp án: D Phương pháp giải: \(AB = \sqrt {{{\left( {{x_B} - {x_A}} \right)}^2} + {{\left( {{y_B} - {y_A}} \right)}^2}} .\) Lời giải chi tiết: \(AB = \sqrt {{{\left( {1 + 3} \right)}^2} + {{\left( {5 - 2} \right)}^2}} = \sqrt {16 + 9} = 5\). Chọn D. Câu hỏi 37 : Trong mp Oxy, cho \(\overrightarrow a = (1; - 2)\), \(\overrightarrow b = (3;4)\), \(\overrightarrow c = (5; - 1)\). Toạ độ vectơ \(\overrightarrow u = 2.\overrightarrow a + \overrightarrow b - \overrightarrow c \) là:
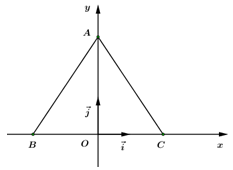
Đáp án: D Phương pháp giải: \(a = \left( {{a_1};{a_2}} \right);\,\,\overrightarrow b = \left( {{b_1};{b_2}} \right) \Rightarrow \overrightarrow a + \overrightarrow b = \left( {{a_1} + {b_1};{a_2} + {b_2}} \right)\) Lời giải chi tiết: Ta có: \(\overrightarrow u = 2.\overrightarrow a + \overrightarrow b - \overrightarrow c = \left( {2.1 + 3 - 5;\,\,2.\left( { - 2} \right) + 4 + 1} \right) = \left( {0;1} \right)\). Chọn D. Câu hỏi 38 : Trong hệ trục tọa độ \(\left( {O;\,\,\overrightarrow i ;\,\,\overrightarrow j } \right),\) cho tam giác đều \(ABC\) cạnh a, biết \(O\) là trung điểm \(BC,\) \(\overrightarrow i \) cùng hướng với \(\overrightarrow {OC} \), \(\overrightarrow j \) cùng hướng với \(\overrightarrow {OA} \). Tìm tọa độ tâm đường tròn ngoại tiếp tam giác \(ABC.\)
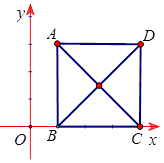
Đáp án: D Phương pháp giải: Vẽ hình và tìm tọa độ các đỉnh của tam giác. Lời giải chi tiết: Theo đề bài ta có hình vẽ như hình bên. Ta có \(O\) là trung điểm của \(BC \Rightarrow OB = OC = \frac{a}{2}\) và \(OA = \sqrt {{a^2} - \frac{{{a^2}}}{4}} = \frac{{a\sqrt 3 }}{2}\) \( \Rightarrow A\left( {0;\frac{{a\sqrt 3 }}{2}} \right),\,\,B\left( { - \frac{a}{2};0} \right),\,\,C\left( {\frac{a}{2};0} \right)\) Tâm đường tròn ngoại tiếp tam giác đều trùng với trọng tâm \(G\left( {0;\frac{{a\sqrt 3 }}{6}} \right).\) Chọn D. Câu hỏi 39 : Trong hệ trục tọa độ \(\left( {O;\,\,\overrightarrow i ;\,\,\overrightarrow j } \right),\) cho hình vuông \(ABCD\) có \(A\left( {1;\,3} \right)\). Biết điểm B thuộc trục \(\left( {O;\,\,\overrightarrow i } \right)\) và \(\overrightarrow {BC} \) cùng hướng với \(\overrightarrow i \). Tìm tọa độ vectơ \(\overrightarrow {AC} \).
Đáp án: C Phương pháp giải: Từ trục tọa độ lấy điểm \(A\) kết hợp giả thiết để suy ra điểm \(B,\,\,C,\,\,D.\) Lời giải chi tiết: Từ giả thiết ta xác định được hình vuông trên mặt phẳng tọa độ như hình vẽ. Theo đề bài ta có: \(B \in \left( {O;\,\,\overrightarrow i } \right),\,\,\overrightarrow {BC} \uparrow \uparrow \overrightarrow i ,\,\,\,A\left( {1;\,\,3} \right) \Rightarrow B\left( {1;\,\,0} \right) \Rightarrow AB = 3.\) \(ABCD\) là hình vuông \( \Rightarrow C\left( {4;\,\,0} \right);\,\,\,D\left( {4;\,\,3} \right).\) \( \Rightarrow \overrightarrow {AC} = \left( {3; - 3} \right).\) Chọn C. Câu hỏi 40 : Cho tam giác \(ABC\) có \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(BC,\,\,CA,\,\,AB\). Biết \(M\left( {1;\,\,1} \right),N\left( { - 2; - 3} \right),P\left( {2; - 1} \right)\). Tìm tọa độ các đỉnh của tam giác \(ABC\).
Đáp án: D Phương pháp giải: \(\overrightarrow {MN} = \overrightarrow {PA} \), từ đó tìm tọa độ điểm Lời giải chi tiết: Gọi \(A\left( {{x_A};\,\,{y_A}} \right).\) Ta có \(\overrightarrow {MN} \left( { - 3; - 4} \right),\,\,\overrightarrow {PA} \left( {{x_A} - 2;{y_A} + 1} \right) \Rightarrow \overrightarrow {MN} = \overrightarrow {PA} \) \( \Leftrightarrow \left\{ \begin{array}{l}{x_A} - 2 = - 3\\{y_A} + 1 = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = - 1\\{y_A} = - 5\end{array} \right. \Rightarrow A\left( { - 1; - 5} \right)\) \(N\) là trung điểm \(AC \Rightarrow C\left( { - 3; - 1} \right).\) \(M\) là trung điểm \(BC \Rightarrow B\left( {5;3} \right).\) Chọn D.
|













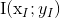 là trung điểm của đoạn thẳng AB.
là trung điểm của đoạn thẳng AB.