Phương pháp giải:

- Tìm điều kiện để phương trình hoành độ giao điểm có 2 nghiệm phân biệt.

- Áp dụng định lí Vi-ét.

Lời giải chi tiết:

Xét phương trình hoành độ giao điểm \({x^2} + 5x + 2m = 0\) (*).

Để đồ thị hàm số \(y = {x^2} + 5x + 2m\) cắt trục Ox tại 2 điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt \( \Leftrightarrow \Delta  = 25 - 8m > 0\) \( \Leftrightarrow m < \frac{{25}}{8}\).

Gọi \({x_1};{x_2}\) là hai nghiệm phân biệt của phương trình (*) \( \Rightarrow A\left( {{x_1};0} \right)\) và \(B\left( {{x_2};0} \right)\).

Áp dụng định lí Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 5\\{x_1}{x_2} = 2m\end{array} \right.\) (**).

Theo bài ra ta có:

OA = 4OB

\( \Leftrightarrow 4\left| {{x_1}} \right| = \left| {{x_2}} \right| \Leftrightarrow \left[ \begin{array}{l}4{x_1} = {x_2}\\ - 4{x_1} = {x_2}\end{array} \right.\)

TH1; \(4{x_1} = {x_2}\), thay vào hệ (**) ta có:

\(\left\{ \begin{array}{l}{x_1} + 4{x_1} = 5\\{x_1}.4{x_1} = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 1\\4 = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_1} = 1\\m = 2\,\,\left( {tm} \right)\end{array} \right.\).

TH1; \( - 4{x_1} = {x_2}\), thay vào hệ (**) ta có:

\(\left\{ \begin{array}{l}{x_1} - 4{x_1} = 5\\{x_1}.\left( { - 4{x_1}} \right) = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_1} =  - \frac{5}{3}\\ - \frac{{100}}{9} = 2m\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_1} =  - \frac{5}{3}\\m =  - \frac{{50}}{9}\,\,\left( {tm} \right)\end{array} \right.\).

\( \Rightarrow S = \left\{ {2; - \frac{{50}}{9}} \right\}\).

Vậy tổng các phần tử của S bằng \(2 + \left( { - \frac{{50}}{9}} \right) =  - \frac{{32}}{9}\).

Đáp án D.

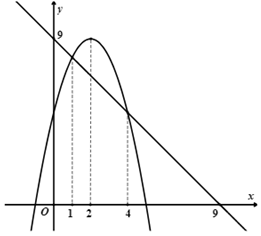
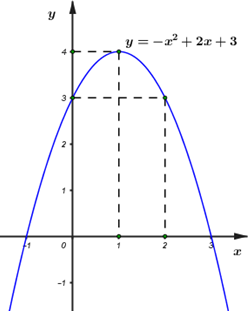
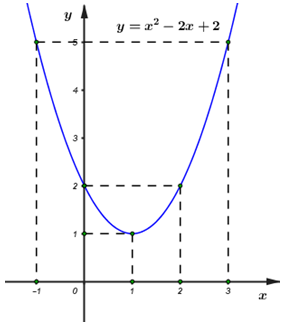
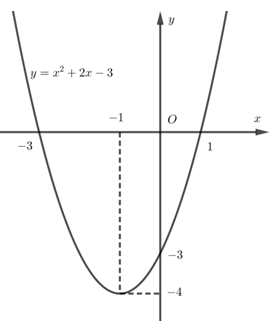
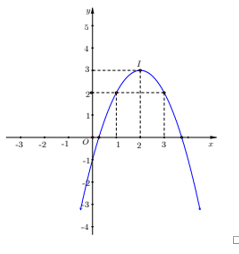
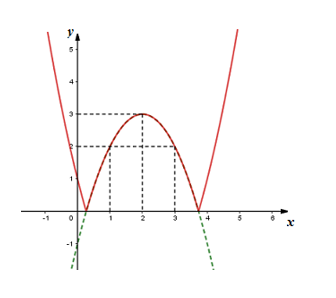
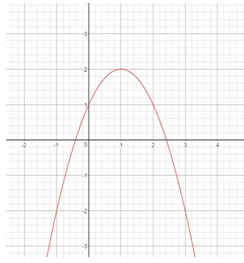
Phương pháp giải:

Đỉnh parabol \(\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\), lập hệ phương trình ẩn \(a,b\).

Lời giải chi tiết:

Ta có: \( - 2 = \frac{{ - b}}{{2a}} \Leftrightarrow  - 4a + b = 0\) (1)

Điểm \(S\left( { - 2; - 1} \right) \in P\) \( \Rightarrow 4a - 2b + 3 \Rightarrow 2a - b =  - 2\)  (2)

Từ (1) và (2) suy ra \(\left\{ \begin{array}{l} - 4a + b = 0\\2a - b =  - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 4\end{array} \right.\)

Vậy \(2a - b = 2 - 4 =  - 2\).

Chọn A.

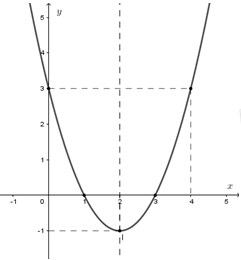
Phương pháp giải:

Từ hình vẽ ta xác định được trục đối xứng của Parabol và tọa độ một số điểm thuộc đồ thị hàm số

Từ đó xác định hệ số \(a,b,c\)

Sau đó tính \(f\left( { - 2} \right).\)

Lời giải chi tiết:

Gọi đường thẳng cắt parabol trên hình vẽ là \(y = mx + n\)

Vì đường thẳng cắt trục tung tại \(\left( {0;9} \right)\) và cắt trục hoành tại \(\left( {9;0} \right)\) nên \(y =  - x + 9\)

Từ đó tọa độ giao điểm của đường thẳng với Parabol lần lượt là \(\left( {4;5} \right);\left( {1;8} \right)\)

Từ hình vẽ ta thấy parabol có trục đối xứng \(x = 2\) và đi qua hai điểm có tọa độ \(\left( {4;5} \right);\left( {1;8} \right)\)

Từ đó ta có hệ :

\(\left\{ \begin{array}{l}16a + 4b + c = 5\\ - \frac{b}{{2a}} = 2\\a + b + c = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + b + c = 8\\b + 4a = 0\\16a + 4b + c = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 1\\b = 4\\c = 5\end{array} \right.\)

Nên \(\left( P \right):y = f\left( x \right) =  - {x^2} + 4x + 5\)

Suy ra \(f\left( { - 2} \right) =  - {\left( { - 2} \right)^2} + 4\left( { - 2} \right) + 5 =  - 7.\)

Chọn B.

Phương pháp giải:

Lập hệ phương trình ẩn \(a,b,c\) dựa vào các điều kiện bài cho.

Giải hệ tìm \(a,b,c\) và kết luận.

Lời giải chi tiết:

Ta có: \( - \frac{b}{{2a}} = 1 \Leftrightarrow 2a + b = 0\)  (1)

Điểm \(I\left( {1;2} \right) \in \left( P \right) \Leftrightarrow 2 = a + b + c\)  (2)

Điểm \(M\left( {2;3} \right) \in \left( P \right) \Leftrightarrow 3 = 4a + 2b + c\) (3)

Từ (1), (2) và (3) ta có: \(\left\{ \begin{array}{l}2a + b = 0\\a + b + c = 2\\4a + 2b + c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 2\\c = 3\end{array} \right.\)

Vậy \(\left( {a;b;c} \right) = \left( {1; - 2;3} \right)\).

Chọn D.

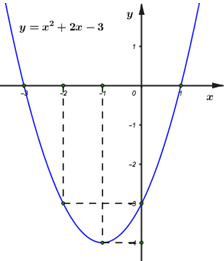
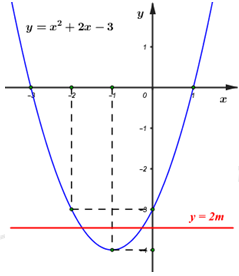
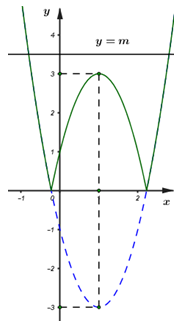
Phương pháp giải:

Sử dụng lý thuyết hàm số bậc hai:

- Trục đối xứng \(x =  - \frac{b}{{2a}}\).

- Điểm \(M \in \left( P \right)\) thì tọa độ của \(M\) thỏa mãn công thức hàm số của \(\left( P \right)\).

Lời giải chi tiết:

- Trục đối xứng \(x =  - 2\) nên \( - \frac{b}{{2a}} =  - 2 \Leftrightarrow b = 4a\) (1)

- Đồ thị đi qua \(A\left( { - 1;9} \right)\) nên \(9 = a.{\left( { - 1} \right)^2} + b.\left( { - 1} \right) + 3\) \( \Leftrightarrow a - b = 6\) (2)

Thay (1) vào (2) ta có: \(a - 4a = 6 \Leftrightarrow  - 3a = 6 \Leftrightarrow a =  - 2\).

Suy ra \(b = 4.\left( { - 2} \right) =  - 8\).

Vậy hàm số \(y =  - 2{x^2} - 8x + 3\).

Chọn A.

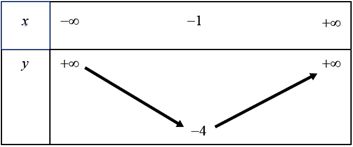
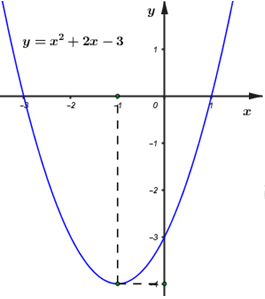
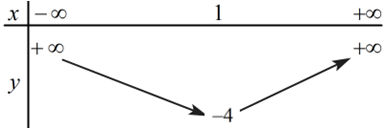
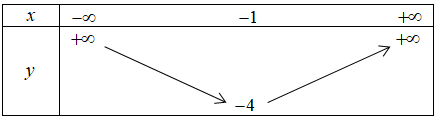
Phương pháp giải:

1) Tìm hoành độ đỉnh, trục đối xứng của Parabol, từ đó suy ra khoảng đồng biến nghịch biến và lập bảng biến thiên.

2) Xét phương trình hoành độ giao điểm tìm nghiệm.

3) Nhận xét điều kiện từ đồ thị đã vẽ.

Lời giải chi tiết:

1) Lập bảng biến thiên và vẽ đồ thị \(\left( P \right)\) của hàm số \(y = {x^2} + 2x-3\)

Ta có: \( - \frac{b}{{2a}} =  - \frac{2}{{2.1}} =  - 1, - \frac{\Delta }{{4a}} =  - 4\)

Vì \(a = 1 > 0\) nên hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\) và đồng biến trên \(\left( { - 1; + \infty } \right)\).

Bảng biến thiên:                        

Đồ thị có: Đỉnh \(P\left( { - 1; - 4} \right)\), cắt \(Ox\) tại \(\left( {1;0} \right),\left( { - 3;0} \right)\), cắt \(Oy\) tại \(\left( {0; - 3} \right)\), đi qua điểm \(\left( { - 2; - 3} \right)\).

Trục đối xứng \(x =  - 1\), bề lõm hướng lên trên.

2) Tìm tọa độ giao điểm của \(\left( P \right)\)và đường thẳng \(d:{\rm{ }}y{\rm{ }} = {\rm{ }}x{\rm{ }}--{\rm{ }}1\)

Xét phương trình hoành độ giao điểm của hai đồ thị hàm số:

\({x^2} + 2x - 3 = x - 1\) \( \Leftrightarrow {x^2} + x - 2 = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 1,y = 0\\x =  - 2,y =  - 3\end{array} \right.\)

Vậy giao điểm là \(A\left( {1;0} \right),B\left( { - 2; - 3} \right)\).

3) Tìm \(m\) sao cho đường thẳng \(y{\rm{ }} = {\rm{ }}2m\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ âm.

Đường thẳng \(y = 2m\) đi qua điểm \(\left( {0;2m} \right)\) và song song hoặc trùng với trục hoành.

Từ đồ thị ta thấy YCBT thỏa mãn khi \( - 4 < 2m <  - 3 \Leftrightarrow  - 2 < m <  - \frac{3}{2}\).

Vậy \( - 2 < m <  - \frac{3}{2}\).

Chọn A.

Phương pháp giải:

a) Tìm trục đối xứng, đỉnh, khoảng đồng biến nghịch biến, lập bảng biến thiên.

Tìm tọa độ các điểm đi qua và vẽ đồ thị.

b) Tìm điều kiện để phương trình có hai nghiệm phân biệt.

- Tìm hai nghiệm và suy ra tọa độ, dùng điều kiện \(OA = 3OB\) tìm \(m\).

Lời giải chi tiết:

a) Lập bảng biến thiên và vẽ đồ thị hàm số trên với \(m = 3.\)

Với \(m = 3\) ta có hàm số \(y = {x^2} - 4x + 3\)

Trục đối xứng \(x = 2.\)

Đỉnh parabol \(I\left( {2; - 1} \right)\)

Vì \(a > 0\) nên đồ thị hàm số quay bề lõm lên trên

BBT:

Hàm số đồng biến trên \(\left( {2; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;2} \right)\)

Bảng giá trị:

Đồ thị hàm số:

b) Tìm  \(m\) sao cho đồ thị cắt \(Ox\) tại \(2\) điểm phân biệt  \(A,\,B\) với  \(OA = 3OB.\)  (1,5đ)

Xét phương trình hoành độ giao điểm \({x^2} - 4x + m = 0\) (1)

Đồ thị cắt \(Ox\) tại hai điểm phân biệt \( \Leftrightarrow \Delta ' = 4 - m > 0 \Leftrightarrow m < 4\).

Khi đó (1) có hai nghiệm phân biệt \({x_1} = 2 - \sqrt {4 - m} ,{x_2} = 2 + \sqrt {4 - m} \).

TH1: \(A\left( {2 + \sqrt {4 - m} ;0} \right),B\left( {2 - \sqrt {4 - m} ;0} \right)\).

\(OA = 3OB\) \( \Leftrightarrow 2 + \sqrt {4 - m}  = 3\left| {2 - \sqrt {4 - m} } \right|\)

\( \Leftrightarrow 4 + 4 - m + 4\sqrt {4 - m} \) \( = 9\left( {4 + 4 - m - 4\sqrt {4 - m} } \right)\)

\( \Leftrightarrow 5\sqrt {4 - m}  = 8 - m\) \( \Leftrightarrow \left\{ \begin{array}{l}8 - m \ge 0\\25\left( {4 - m} \right) = 64 - 16m + {m^2}\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}m \le 8\\{m^2} + 9m - 36 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}m \le 8\\m = 3,m =  - 12\end{array} \right. \Leftrightarrow m = 3\,\,\,\left( {tm} \right)\)

Vậy \(m = 3\).

TH2: \(A\left( {2 - \sqrt {4 - m} ;0} \right),B\left( {2 + \sqrt {4 - m} ;0} \right)\).

\(OA = 3OB\) \( \Leftrightarrow \left| {2 - \sqrt {4 - m} } \right| = 3\left( {2 + \sqrt {4 - m} } \right)\)

\( \Leftrightarrow 4 + 4 - m - 4\sqrt {4 - m} \) \( = 9\left( {4 + 4 - m + 4\sqrt {4 - m} } \right)\)

\( \Leftrightarrow 5\sqrt {4 - m}  = m - 8\) (vô nghiệm do \(m < 4\) thì \(m - 8 < 0\))

Vậy có một giá trị duy nhất là \(m = 3\).

Chọn C.

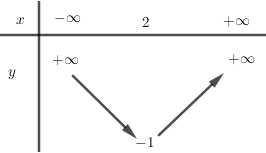
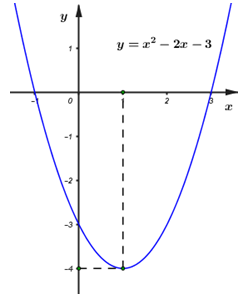
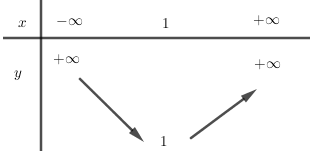
Phương pháp giải:

a) Tìm trục đối xứng, tọa độ đỉnh, khoảng đồng biến nghịch biến lập bảng biến thiên.

Tìm tọa độ các điểm đi qua và vẽ đồ thị.

b) Xét phương trình hoành độ giao điểm và tìm nghiệm, từ đó suy ra điều kiện.

Lời giải chi tiết:

a)  (1 điểm) Lập bảng biến thiên và vẽ đồ thị \(\left( P \right)\) của hàm số trên.

+) \( - \frac{b}{{2a}} = 1;\, - \frac{\Delta }{{4a}} = 4.\) Đỉnh \(I\left( {1;4} \right).\)

+) Trục đối xứng : \(x = 1.\)

+) Bảng biến thiên :

Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\), nghịch biến trên khoảng \(\left( {1; + \infty } \right).\)

Bảng giá trị

Đồ thị:

Cắt trục \(Oy\) tại \(\left( {0;3} \right)\), cắt trục \(Ox\) tại \(\left( { - 1;0} \right),\left( {3;0} \right)\).

Có trục đối xứng \(x = 1\), đỉnh \(\left( {1;4} \right)\).

b) (1 điểm) Tìm điều kiện của tham số \(m\) để đường thẳng \(y = 2mx - 4m + 3\) cắt \(\left( P \right)\) tại \(2\) điểm phân biệt có hoành độ lớn hơn \(1.\)

Xét phương trình: \({x^2} + 2\left( {m - 1} \right)x - 4m = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x =  - 2m\end{array} \right.\)

Yêu cầu bài toán \( \Leftrightarrow \left\{ \begin{array}{l} - 2m > 1\\ - 2m \ne 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < \frac{{ - 1}}{2}\\m \ne  - 1\end{array} \right.\)

\(KL:\, - 1 \ne m < \frac{{ - 1}}{2}.\)

Chọn A.

Phương pháp giải:

1) Sử dụng định nghĩa về hàm số chẵn, lẻ.

2) Lập bảng biến thiên và vẽ đồ thị như sách giáo khoa.

3) Thay tọa độ các điểm vào hàm số, sử dụng công thực tọa độ đỉnh.

Lời giải chi tiết:

1) Xét tính chẵn, lẻ của hàm số \(f\left( x \right) = {x^4} - 3{x^2} + 2.\)

Tập xác định : \(D = \mathbb{R}.\)

\( \Rightarrow \forall \,\,x \in D \Rightarrow  - x \in D.\)

Xét \(f\left( { - x} \right) = {\left( { - x} \right)^4} - 3{\left( { - x} \right)^2} + 2 = {x^4} - 3{x^2} + 2 \Rightarrow f\left( x \right) = f\left( { - x} \right).\)

Vậy \(f\left( x \right)\) là hàm số chẵn.

2) Lập bảng biến thiên và vẽ đồ thị hàm số : \(y = {x^2} + 2x - 3.\)

Tập xác định : \(D = \mathbb{R}.\)

Bảng biến thiên:

Đồ thị hàm số có đỉnh \(I\left( { - 1; - 4} \right)\) và nhận đường thẳng \(x =  - 1\) làm trục đối xứng.

Đồ thị hàm số:

3) Xác định \(a,\,\,b,\,\,c\) để parabol \(\left( P \right):\,\,y = a{x^2} + bx + c\) đi qua điểm \(A\left( {2;\,\,1} \right)\) và có đỉnh \(I\left( {1; - 1} \right).\)

Parabol đi qua điểm \(A\left( {2;1} \right)\) và có đỉnh \(I\left( {1; - 1} \right)\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}a{.2^2} + b.2 + c = 1\\\frac{{ - b}}{{2a}} = 1\\\frac{{ - \left( {{b^2} - 4ac} \right)}}{{4a}} =  - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\2a + b = 0\\{b^2} - 4ac - 4a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\b =  - 2a\\{\left( { - 2a} \right)^2} - 4ac - 4a = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\b =  - 2a\\4a\left( {a - c - 1} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b + c = 1\\2a + b = 0\\a - c = 1\,\,\,\left( {do\,\,\,a \ne 0} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - 4\\c = 1\end{array} \right..\end{array}\)

Vậy \(a = 2,b =  - 4,c = 1.\)

Chọn A.

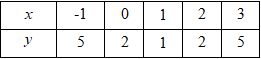
Phương pháp giải:

Cho parabol \(\left( P \right):\,\,\,y = a{x^2} + bx + c\,\,\,\left( {a \ne 0} \right)\) có tọa độ đỉnh là: \(I\left( { - \frac{b}{{2a}};\,\, - \frac{\Delta }{{4a}}} \right).\)

Lời giải chi tiết:

Vì \(\left( P \right)\) là parabol nên ta có \(a \ne 0.\)

Đồ thị \(\left( P \right)\) có điểm thấp nhất là \(B\left( { - 2;\,\,\,4} \right) \Rightarrow \) đồ thị hàm số có bề lõm hướng xuống dưới hay \(a > 0\) và \(B\) là đỉnh của đổ thị hàm số.

\( \Leftrightarrow \left\{ \begin{array}{l}\frac{{ - b}}{{2a}} =  - 2\\\frac{{ - \left( {{b^2} - 4ac} \right)}}{{4a}} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4a\\{b^2} - 4ac =  - 16a\end{array} \right.\)

Đồ thị \(\left( P \right)\) đi qua điểm \(A\left( {0;6} \right) \Rightarrow a{.0^2} + b.0 + c = 6 \Rightarrow c = 6.\)

Thay \(c = 6\) vào hệ trên ta được hệ phương trình:

\( \Leftrightarrow \left\{ \begin{array}{l}b = 4a\\{b^2} - 24a =  - 16a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4a\\{b^2} = 8a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4a\\16{a^2} - 8a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4a\\\left[ \begin{array}{l}a = 0\\a = \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = 2\end{array} \right..\)

Vậy parabol \(\left( P \right):\,\,y = \frac{1}{2}{x^2} + 2x + 6.\)

Chọn B.

Phương pháp giải:

Làm theo các bước khảo sát và vẽ đồ thị hàm số.

Lời giải chi tiết:

Khảo sát sự biến thiên và vẽ đồ thị hàm số \(y = {x^2} - 2x - 3.\)

* Tập xác định: \(D = \mathbb{R}\)

* Tọa độ đỉnh: \(I\left( {1; - \,4} \right).\)

* Sự biến thiên:

Vì \(a = 1 > 0\) nên hàm số đồng biến trên khoảng \(\left( {1; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ;1} \right).\)

Bảng biến thiên:

* Điểm đặc biệt:

* Đồ thị: Đồ thị hàm số là đường parabol có đỉnh \(I\left( {1; - 4} \right)\), hướng bề lõm lên trên và nhận đường thẳng \(x = 1\) làm trục đối xứng.

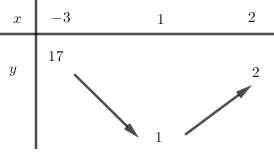
Phương pháp giải:

a) Với \(a > 0\) thì hàm số \(y = a{x^2} + bx + c\) đồng biến trên \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\)

b) Lập BBT của hàm số đã cho trên đoạn \(\left[ { - 3;2} \right]\) từ đó xác định GTLN và GTNN.

Lời giải chi tiết:

a) Lập bảng biến thiên và vẽ đồ thị của hàm số \(y = {x^2} - 2x + 2\).

Tập xác định: \(D = R\)

Đỉnh Parbol: \(I\left( {1;1} \right)\)

BBT:

Bảng giá trị:

Đồ thị hàm số:

b) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {x^2} - 2x + 2\) trên đoạn \(\left[ { - 3;2} \right]\).

BBT của hàm số \(y = {x^2} - 2x + 2\) trên đoạn \(\left[ { - 3;2} \right]\)

Từ BBT ta có:  GTLN của hàm số trên \(\left[ { - 3;2} \right]\) là \(y = 17 \Leftrightarrow x =  - 3\)

GTNN của hàm số trên \(\left[ { - 3;2} \right]\) là \(y = 2 \Leftrightarrow x = 2\)

Chọn D.

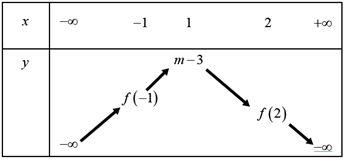
Phương pháp giải:

Dùng bảng biến thiên tìm giá trị lớn nhất của hàm số.

Lời giải chi tiết:

Xét hàm số: \(y =  - {x^2} + 2x + m - 4\) ta có tọa độ đỉnh của đồ thị hàm số là: \(I\left( {1;\,\,m - 3} \right)\)

Ta có BBT:

Từ bảng biến thiên suy ra giá trị lớn nhất của hàm số trên \(\left[ { - 1;2} \right]\) là \(m - 3.\)

Giá trị lớn nhất của hàm số trên \(\left[ { - 1;2} \right]\) bằng  \(3 \Leftrightarrow m - 3 = 3 \Leftrightarrow m = 6.\)

\( \Rightarrow m \in \left( {5;\,\,7} \right).\)

Chọn C.

Phương pháp giải:

- Lập hàm số biểu thị số cá thu hoạch được sau mỗi vụ theo \(x\).

- Tìm GTLN của hàm số và kết luận.

Lời giải chi tiết:

Sau mỗi vụ thu hoạch được số gam cá là: \(f\left( x \right) = x\left( {480 - 20x} \right) =  - 20{x^2} + 480x\).

Có \( - \frac{b}{{2a}} =  - \frac{{480}}{{2.\left( { - 20} \right)}} = 12\) nên hàm số đạt GTLN tại \(x = 12\).

Chọn B.

Phương pháp giải:

Hàm số: \(y = a{x^2} + bx + c\,\) với \(a < 0\) tăng (đồng biến) trên \(\left( { - \infty ;\,\, - \frac{b}{{2a}}} \right)\) và giảm (nghịch biến) trên \(\left( { - \frac{b}{{2a}}; + \infty } \right).\)

Lời giải chi tiết:

Ta có: \(y =  - {x^2} + 4x + 2\) có \(a =  - 1 < 0\)

\( \Rightarrow \) Hàm số tăng trên \(\left( { - \infty ;\,\,2} \right)\) và giảm trên \(\left( {2; + \infty } \right).\)

\( \Rightarrow \) Trong các đáp án, chỉ có đáp án A đúng.  

Chọn A.

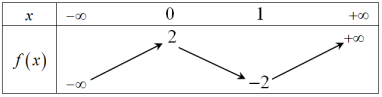
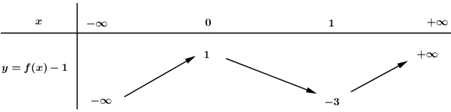
Phương pháp giải:

+) Số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là số giao điểm của hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right).\)

+) Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a \ne 0}\\{\Delta  = {b^2} - 4ac > 0}\end{array}} \right.\)

Lời giải chi tiết:

Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(d\) là :

\(\begin{array}{l}{x^2} - 4x + 3 = mx + 3 \Leftrightarrow x\left[ {x - \left( {m + 4} \right)} \right] = 0\,\,\,\,\left( * \right)\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\x - \left( {m + 4} \right) = 0\end{array} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = m + 4}\end{array}} \right.\end{array}\) 

\( \Rightarrow d\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A,B\,\, \Leftrightarrow \,\left( * \right)\) có hai nghiệm phân biệt

\( \Leftrightarrow 4 + m \ne 0 \Leftrightarrow m \ne  - 4.\)

+) Với \(x = 0 \Rightarrow y = 3 \Rightarrow A\left( {0;\,\,3} \right) \Rightarrow A \in Oy.\)

+) Với \(x = m + 4 \Rightarrow y = {m^2} + 4m + 3 \Rightarrow B\left( {m + 4;\,\,{m^2} + 4m + 3} \right).\)

Gọi \(H\)  là hình chiếu của \(B\) lên \(OA\) \((H\) là hình chiếu của \(B\) trên \(Oy).\)

\( \Rightarrow H\left( {0;\,\,{m^2} + 4m + 3} \right) \Rightarrow BH = \left| {{x_B}} \right| = \left| {4 + m} \right|.\) 

Theo giả thiết bài toán, ta có:

\({S_{\Delta OAB}} = \frac{9}{2} \Leftrightarrow \frac{1}{2}.OA.BH = \frac{9}{2} \Leftrightarrow \frac{1}{2}.3.\left| {m + 4} \right| = \frac{9}{2} \Leftrightarrow \left| {m + 4} \right| = 3 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m =  - 1\,\,\,\,\,\,\left( {tm} \right)}\\{m =  - 7\,\,\,\,\left( {tm} \right)}\end{array}} \right..\)

Chọn  D.

Phương pháp giải:

+) Từ hàm số \(y = f\left( x \right)\) có đồ thị \(\left( C \right)\) hãy suy ra đồ thị: \(y = f\left( x \right) - a\,\,\,\,\,\left( {a > 0} \right) \Rightarrow \) Tịnh tiến \(\left( C \right)\) xuống dưới \(a\) đơn vị theo phương \(Oy.\)

+) Vẽ đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)theo các bước sau:

B1: Giữ nguyên đồ thị \(y = f\left( x \right)\) \(\left( C \right)\) ở phía trên trục \(Ox.\)

B2: Xoá phần đồ thị \(\left( C \right)\) ở phía dưới \(Ox.\)

B3: Lấy đối xứng phần đồ thị \(\left( C \right)\) phía dưới lên trên qua trục \(Ox.\)

+) Số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là số giao điểm của hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right).\)

Lời giải chi tiết:

Dựa vào BBT của hàm số \(y = f\left( x \right),\) ta suy ra BBT của hàm số \(y = f\left( x \right) - 1:\) :

Dựa vào BBT của hàm số \(y = f\left( x \right) - 1,\) ta suy ra BBT của hàm số \(y = \left| {f\left( x \right) - 1} \right|\) :

Từ BBT, suy ra PT: \(\left| {f\left( x \right) - 1} \right| = 2m + 1\) có 4 nghiệm phân biệt \( \Leftrightarrow 1 < 2m + 1 < 3 \Leftrightarrow 0 < m < 1\)

Chọn B.

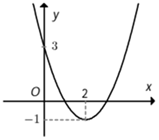
Phương pháp giải:

B1: Tham số hoá toạ độ điểm \(M\)

B2: Tính \(AM.\) Từ đó, quan sát các phương án để loại trừ và tính toán để đưa ra đáp án đúng.

Lời giải chi tiết:

Vì \(M \in \left( P \right):y = {x^2} \Rightarrow M\left( {t;{t^2}} \right) \Rightarrow \) loại C, D.

Ta có: \(AM = \sqrt {{{\left( {t - 2} \right)}^2} + {t^4}} .\) 

Đến đây, cách làm nhanh nhất là ta thay tọa độ điểm \(M\) ở hai đáp án A, B vào công thức tính độ dài \(AM\) để chọn đáp án đúng:

+) Với \(M\left( {1;\,\,1} \right) \Rightarrow AM = \sqrt {{{\left( {1 - 2} \right)}^2} + {1^4}}  = \sqrt 2 .\)

+) Với \(M\left( { - 1;\,\,1} \right) \Rightarrow AM = \sqrt {{{\left( { - 1 - 2} \right)}^2} + {{\left( { - 1} \right)}^4}}  = \sqrt {10} .\)

Vậy \(M\left( {1;\,\,1} \right)\) thỏa mãn bài toán.

Chọn  A.

Phương pháp giải:

+) Vẽ đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)theo các bước sau:

B1: Giữ nguyên đồ thị \(y = f\left( x \right)\) \(\left( C \right)\) ở phía trên trục \(Ox.\)

B2: Xoá phần đồ thị \(\left( C \right)\) ở phía dưới \(Ox.\)

B3: Lấy đối xứng phần đồ thị \(\left( C \right)\) phía dưới lên trên qua trục \(Ox.\)

+) Số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là số giao điểm của hai đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right).\)

Lời giải chi tiết:

+) Phương trình \(\left| {f\left( x \right)} \right| - 1 = m \Leftrightarrow \left| {f\left( x \right)} \right| = m + 1.\)

+) Đồ thị của hàm số \(y = \left| {f\left( x \right)} \right|\) là:

Dựa vào đồ thị, để phương trình \(\left| {f\left( x \right)} \right| = m + 1\) có hai nghiệm phân biệt  \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m + 1 > 1}\\{m + 1 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m > 0}\\{m =  - 1}\end{array}} \right.} \right.\)

Chọn  C

Phương pháp giải:

Đồ thị hàm số \(y = a{x^2} + bx + c\,\,(a \ne 0)\) là parabol có đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)

Thay tọa độ các điểm vào hàm số để có được hệ phương trình, giải để tìm a, b, c.

Lời giải chi tiết:

Parabol (P) : \(y = a{x^2} + bx + c,\,\,a \ne 0\) biết (P) đi qua \(A\left( {2;{\rm{ }}3} \right)\) và có đỉnh \(I\left( {1;{\rm{ }}2} \right).\)

\( \Rightarrow \left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = 1\\4a + 2b + c = 3\\a + b + c = 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2a + b = 0\\4a + 2b + c = 3\\a + b + c = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 2\\c = 3\end{array} \right. \Rightarrow y = {x^2} - 2x + 3\) 

Chọn C.

Phương pháp giải:

Đồ thị hàm số \(y = a{x^2} + bx + c\,\,(a \ne 0)\) là parabol có đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)

Lời giải chi tiết:

Hàm có có giá trị nhỏ nhất \( \Rightarrow a > 0\) và \({y_{\min }} = {y_I}\) là giá trị nhất của hàm số tại \(x = {x_I}\)

Từ dữ kiện đề bài ta có hệ phương trình:

\(\left\{ \begin{array}{l}{x_I} = \frac{1}{2}\\{y_I} = y\left( {\frac{1}{2}} \right) = \frac{3}{4}\\y\left( 1 \right) = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - \frac{b}{{2a}} = \frac{1}{2}\\\frac{1}{4}a + \frac{1}{2}b + c = \frac{3}{4}\\a + b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\;\;\left( {tm} \right)\\b =  - 1\\c = 1\end{array} \right. \Rightarrow y = {x^2} - x + 1\)

Chọn B.

Phương pháp giải:

Đồ thị hàm số \(y = a{x^2} + bx + c\,\,(a \ne 0)\) là parabol có đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)

Lời giải chi tiết:

Đồ thị hàm số \(y = a{x^2} + bx + c\,\,(a \ne 0)\) cắt trục tung tại điểm có tung độ bằng 2

\( \Rightarrow \) đồ thị hàm số đi qua điểm \(\left( {0;\;2} \right) \Rightarrow c = 2.\)

Lại có đồ thị hàm số có đỉnh là \(I\left( {\frac{1}{4};\;\frac{5}{4}} \right)\)  nên ta có hệ phương trình:

\(\left\{ \begin{array}{l} - \frac{b}{{2a}} = \frac{1}{4}\\\frac{1}{{16}}a + \frac{1}{4}b + c = \frac{5}{4}\\c = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2a =  - 4b\\a + 4b + 16c = 20\\c = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 12\\b =  - 6\\c = 2\end{array} \right.\)

Chọn C.

Phương pháp giải:

Thay tọa độ các điểm A, B, C vào phương trình của parabol, giải hệ phương trình để tìm a, b, c ta lập được phương trình của parabol.

Lời giải chi tiết:

Parabol \(y = a{x^2} + bx + c\) đi qua \(A\left( {0;--1} \right),{\rm{ }}B\left( {1;--1} \right),{\rm{ }}C\left( {--1;{\rm{ }}1} \right)\)

\( \Rightarrow \left\{ \begin{array}{l}c =  - 1\\a + b + c =  - 1\\a - b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 1\\c =  - 1\end{array} \right. \Rightarrow \left( P \right):\;\;y = {x^2} - x - 1.\)

Chọn B.

Phương pháp giải:

a) Đồ thị hàm số \(y = a{x^2} + bx + c\,\,(a \ne 0)\) là parabol có đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)

b) Áp dụng đầy đủ các bước lập BBT của đồ thị hàm số \(y = a{x^2} + bx + c\) sau đó vẽ đồ thị hàm số.

Lời giải chi tiết:

a) Viết phương trình parabol (P): \(y = a{x^2} + bx + c\) biết (P) đi qua điểm \(M( - 2; - 3)\)và nhận điểm \(I( - 1; - 4)\) làm đỉnh.

Theo đề bài ta có: \(\left\{ \begin{array}{l}a \ne 0\\4a - 2b + c =  - 3\\\frac{{ - b}}{{2a}} =  - 1\\a - b + c =  - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\4a - 2b + c =  - 3\\2a - b = 0\\a - b + c =  - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\a = 1\\b = 2\\c =  - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c =  - 3\end{array} \right..\)

Vậy phương trình parabol  (P): \(y = {x^2} + 2x - 3\)

b) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} + 2x - 3\)

+ Tập xác định \(D = R\).

+ Bảng biến thiên:

+ Vẽ đồ thị hàm số

+ Đỉnh \(I\left( { - 1; - 4} \right)\)

+ Trục đối xứng \(x =  - 1\)

+ Giao với trục tung \(A\left( {0; - 3} \right)\)

+ Giao với  trục hoành tại \(B\left( {1;0} \right);\,\,B'\left( { - 3;0} \right)\).

Phương pháp giải:

Thay tọa độ các điểm vào hàm số để tìm b, c từ đó tìm khẳng định đúng.

Lời giải chi tiết:

Đồ thị hàm số \(y = {x^2} + bx + c\) đi qua các điểm \(A\left( {0;2} \right)\,\,,\,\,B\left( {1;5} \right)\)

\( \Rightarrow \left\{ \begin{array}{l}c = 2\\1 + b + c = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 2\\b = 2\end{array} \right.\) \( \Rightarrow \) Hàm số \(y = {x^2} + 2x + 2 = {\left( {x + 1} \right)^2} + 1 \ge 1\) với mọi x thuộc tập xác định

 \( \Rightarrow \) Giá trị nhỏ nhất của hàm số bằng 1

Chọn A.

Phương pháp giải:

Đồ thị hàm số \(y = a{x^2} + bx + c\,\,(a \ne 0)\) là parabol có đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)

Lời giải chi tiết:

\(y = m{x^2} - 2mx - {m^2} - 1\,\,(m \ne 0)\) có đỉnh là  I

\(\Delta  = 4{m^2} + 4m\left( {{m^2} + 1} \right) = 4{m^3} + 4{m^2} + 4m\)

\( \Rightarrow I\left( {1; - {m^2} - m - 1} \right)\)

Để  I  nằm trên đường thẳng \(y = x - 2 \Leftrightarrow  - {m^2} - m - 1 = 1 - 2 \Leftrightarrow  - {m^2} - m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\;\;\left( {ktm} \right)\\m =  - 1\;\;\left( {tm} \right)\end{array} \right.\) 

Vậy \(m \in \left( { - 2;2} \right)\) 

Chọn C.

Phương pháp giải:

Đồ thị hàm số \(y = a{x^2} + bx + c\,\,(a \ne 0)\) là parabol có đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)

Lời giải chi tiết:

Parabol  \((P):y = {x^2} + ax + b\) có đỉnh \(I\left( { - \frac{a}{2}; - \frac{\Delta }{4}} \right)\)

Để  Parabol  (P) có đỉnh \(I\left( {1;\;2} \right) \Leftrightarrow \left\{ \begin{array}{l} - \frac{a}{2} = 1\\ - \frac{{{a^2} - 4b}}{4} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 2\\{a^2} - 4b + 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - 2\\b = 3\end{array} \right..\)

Chọn A.

Phương pháp giải:

Parabol \(\left( P \right):y = a\,{x^2} + bx + c,\,\,\left( {a \ne 0} \right)\) có trục đối xứng \(x =  - \frac{b}{{2a}}\).

Lời giải chi tiết:

Parabol \(y = a{x^2} + bx + c\) đi qua điểm \(M\left( {1; - 1} \right)\) và có trục đối xứng \(x = 2\) 

\( \Leftrightarrow \left\{ \begin{array}{l} - 1 = a{.1^2} + b.1 + 2\\ - \frac{b}{{2a}} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a + b =  - 3\\b =  - 4a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 4\end{array} \right. \Rightarrow y = {x^2} - 4x + 2\).

Chọn: A

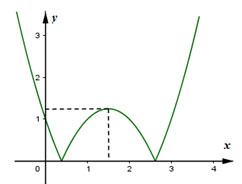
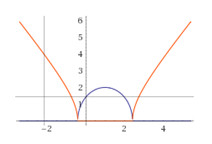
Phương pháp giải:

Vẽ đồ thị hàm số \(y = \left| {{x^2} - 3x + 1} \right|\). Tìm điều kiện của m để đường thẳng \(y = m\) cắt \(y = \left| {{x^2} - 3x + 1} \right|\) tại 4 điểm phân biệt.

Lời giải chi tiết:

\(y = \left| {{x^2} - 3x + 1} \right| = \left[ \begin{array}{l}{x^2} - 3x + 1\,\,khi\,\,x \in \left( { - \infty ;\frac{{3 - \sqrt 5 }}{2}} \right) \cup \left( {\frac{{3 + \sqrt 5 }}{2}; + \infty } \right)\\ - {x^2} + 3x - 1\,\,khi\,\,x \in \left( {\frac{{3 - \sqrt 5 }}{2};\frac{{3 + \sqrt 5 }}{2}} \right)\end{array} \right.\)

Vẽ hai đồ thị hàm số trên cùng 1 mặt phẳng tọa độ :

Hàm số \(y =  - {x^2} + 3x - 1\) có tọa độ đỉnh \(I\left( {\frac{3}{2};\frac{5}{4}} \right)\)

Để đồ thị hàm số \(y = \left| {{x^2} - 3x + 1} \right|\) cắt đường thẳng \(y = m\) tại 4 điểm phân biệt \( \Leftrightarrow 0 < m < \frac{5}{4}\).

Chọn B.

Phương pháp giải:

Số nghiệm của phương trình \(\left| {a{x^2} + bx + c} \right| = m\) là số giao điểm của đồ thị hàm số \(y = \left| {a{x^2} + bx + c} \right|\) và đường thẳng \(y = m\).

Lời giải chi tiết:

Từ đồ thị hàm số \(\left( P \right):\,\,y = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) ta suy ra đồ thị hàm số \(y = \left| {a{x^2} + bx + c} \right|\) như sau:

Dựa vào đồ thị hàm số ta thấy để đường thẳng \(y = m\) cắt đồ thị hàm số \(y = \left| {a{x^2} + bx + c} \right|\) tại 4 điểm phân biệt \( \Leftrightarrow 0 < m < 3\).

Chọn B.

Phương pháp giải:

Đường thẳng d cắt parabol (P) tại hai điểm phân biệt khi và chỉ khi phương trình hoành độ giao điểm có 2 nghiệm phân biệt.

Lời giải chi tiết:

Xét phương trình hoành độ giao điểm \({x^2} + 4x + 6 + 2m = 0\,\,\left( 1 \right)\) 

Để đường thẳng d: \(y =  - 2m\) cắt parabol (P): \(y = {x^2} + 4x + 6\) tại hai điểm phân biệt thì phương trình (1) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' > 0 \Leftrightarrow 4 - 6 - 2m > 0 \Leftrightarrow m <  - 1.\) 

Chọn B.

Phương pháp giải:

Số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và \(y = g\left( x \right)\) là số nghiệm của phương trình hoành độ giao điểm \(f\left( x \right) = g\left( x \right).\)

Lời giải chi tiết:

Xét phương trình hoành độ giao điểm 

\(3{x^2} - 6x + 5 = 1 - m \Leftrightarrow 3{x^2} - 6x + m + 4 = 0\,\,\left( * \right).\)

Để (P) và d cắt nhau tại 2 điểm phân biệt thì phương trình (*) có 2 nghiệm phân biệt

\( \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3 \ne 0\\9 - 3\left( {m + 4} \right) > 0\end{array} \right. \Leftrightarrow m < - 1.\)

Chọn B

Phương pháp giải:

Thay tọa độ các điểm A, B, C vào hàm số suy ra hệ ba phương trình ba ẩn, giải hệ phương trình tìm a, b, c.

Lời giải chi tiết:

Vì A, B, C thuộc parabol nên ta có:  \(\left\{ \matrix{- 1 = c \hfill \cr - 1 = a + b + c \hfill \cr 1 = a - b + c \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{a = 1 \hfill \cr b = - 1 \hfill \cr c = - 1 \hfill \cr} \right.\)

Chọn A.

Phương pháp giải:

Thiết lập phương trình hoành độ giao điểm sau đó tìm tọa độ trung điểm.

Trung điểm của AB có tọa độ \(\left( {{{{x_A} + {x_B}} \over 2},{{{y_A} + {y_B}} \over 2}} \right).\)

Lời giải chi tiết:

Phương trình hoành độ giao điểm của (P) và (d) là: \({x^2} - x + 1 = mx \Leftrightarrow {x^2} - \left( {m + 1} \right)x + 1 = 0\,\,\left( * \right)\).

Để (d) và (P) cắt nhau tại 2 điểm phân biệt A và B thì phương trình (*) có 2 nghiệm phân biệt

\( \Leftrightarrow \left\{ \matrix{  a \ne 0 \hfill \cr   \Delta  > 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  1 \ne 0 \hfill \cr   {\left( {m + 1} \right)^2} - 4 > 0 \hfill \cr}  \right. \Leftrightarrow {m^2} + 2m - 3 > 0 \Leftrightarrow \left[ \matrix{  x > 1 \hfill \cr   x <  - 3 \hfill \cr}  \right.\)

Khi đó theo hệ thức Vi-et ta có: \(\left\{ \matrix{  {x_A} + {x_B} =  - {b \over a} = m + 1 \hfill \cr   {x_A}{x_B} -  = {c \over a} = 1 \hfill \cr}  \right.\)

Gọi C là trung điểm của AB \( \Rightarrow C\left( {{{{x_A} + {x_B}} \over 2},{{{y_A} + {y_B}} \over 2}} \right) \Rightarrow {x_C} = x = {{m + 1} \over 2}\)

\({y_C} = {{{y_A} + {y_B}} \over 2} = {{m{x_A} + m{x_B}} \over 2} = {{m\left( {{x_A} + {x_B}} \right)} \over 2} = {{m\left( {m + 1} \right)} \over 2}.\)

Vậy \(C\left( {{{m + 1} \over 2};\,\,{{m\left( {m + 1} \right)} \over 2}} \right)\).

Chọn A.

Phương pháp giải:

a) Thực hiện đầy đủ các bước lập BBT và vẽ đồ thị hàm số (P).

b) Để đường thẳng \(y = x + 2m - 1\) cắt đồ thị (P) tại hai điểm phân biệt cùng phía với trục Oy khi và chỉ khi phương trình hoành độ giao điểm có hai nghiệm dương phân biệt.

Lời giải chi tiết:

a) TXĐ: D = R.

Ta có: \( - \frac{b}{{2a}} =  - \frac{{ - 4}}{{2.1}} = 2\) 

Khi x = 2 thì y = -1. (P) có đỉnh \(I\left( {2; - 1} \right)\) và có trục đối xứng x = 2.

a = 1 > 0 nên hàm số đồng biến trên \(\left( {2; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;2} \right)\)

Ta có BBT:

Vẽ đồ thị hàm số:

Giao điểm của đồ thị hàm số với trục Ox là (3; 0) và (1; 0)

Giao điểm của đồ thị hàm số với trục Oy là (0; 3).

Phương pháp giải:

Vẽ được đồ thị hàm số \(y = \left| {2{x^2} - 4x - 1} \right|\) và dựa vào đồ thị, tìm giao với đường thẳng \(y = m\)

Lời giải chi tiết:

Vẽ đồ thị \(y = \left| {2{x^2} - 4x - 1} \right|\) bằng cách:

Giữ nguyên phần nằm trên \(Ox\)  của đồ thị hàm số \(y = 2{x^2} - 4x - 1\);

Lấy đối xứng phần nằm dưới \(Ox\)  qua \(Ox.\)

Xóa bỏ phần nằm dưới \(Ox.\)

Ta có đồ thị hàm số như hình vẽ bên.

Nghiệm của \(\left| {2{x^2} - 4x - 1} \right| = m\) là giao của 2 đồ thị hàm số \(y = \left| {2{x^2} - 4x - 1} \right|\)

và \(y = m\) với \(y = m\) là đường thẳng song song \(Ox.\)

Khi đó để phương trình có 2 nghiệm thì \(\left[ \begin{array}{l}m = 0\\m > 3\end{array} \right.\)

Chọn B.

Phương pháp giải:

Lập phương trình hoành độ giao điểm \(\left( * \right)\)  của hai đồ thị hàm số.

Tìm điều kiện của \(m\) để phương trình \(\left( * \right)\) có hai nghiệm phân biệt.

Áp dụng định lý Vi-et để tìm giá trị nhỏ nhất của biểu thức \(O{A^2} + O{B^2}.\)

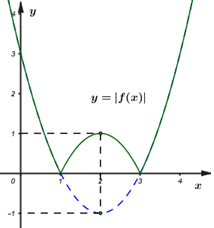
Lời giải chi tiết:

Xét phương trình hoành độ giao điểm của hai đồ thị hàm số:

\({x^2} - 2x - 2 = x + m \Leftrightarrow {x^2} - 3x - m - 2 = 0\,\,\,\,\,\,\left( * \right)\)

\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt

\( \Leftrightarrow \Delta  > 0 \Leftrightarrow 9 + 4\left( {m + 2} \right) > 0 \Leftrightarrow 4m + 17 > 0 \Leftrightarrow m >  - \frac{{17}}{4}.\)

Gọi \(A\left( {{x_A};\,\,{y_A}} \right),\,\,\,B\left( {{x_B};\,\,{y_B}} \right)\) là hai giao điểm của hai đồ thị hàm số.

\( \Rightarrow {x_A};\,\,{x_B}\) là hai nghiệm của phương trình \(\left( * \right).\)

Áp dụng định lý Vi-et ta có:\(\left\{ \begin{array}{l}{x_A} + {x_B} = 3\\{x_A}{x_B} =  - m - 2\end{array} \right..\)

Ta có: \(OA = \sqrt {x_A^2 + y_A^2} ,\,\,\,OB = \sqrt {x_B^2 + y_B^2} \)

\(\begin{array}{l} \Rightarrow O{A^2} + O{B^2} = x_A^2 + y_A^2 + x_B^2 + y_B^2 = \left( {x_A^2 + x_B^2} \right) + \left( {y_A^2 + y_B^2} \right)\\ = \left( {x_A^2 + x_B^2} \right) + \left[ {{{\left( {{x_A} + m} \right)}^2} + {{\left( {{x_B} + m} \right)}^2}} \right]\\ = x_A^2 + x_B^2 + x_A^2 + x_B^2 + 2m\left( {{x_A} + {x_B}} \right) + 2{m^2}\\ = 2{\left( {{x_A} + {x_B}} \right)^2} - 4{x_A}{x_B} + 2m\left( {{x_A} + {x_B}} \right) + 2{m^2}\end{array}\)

\(\begin{array}{l} = {2.3^2} + 4\left( {m + 2} \right) + 2m.3 + 2{m^2}\\ = 2{m^2} + 10m + 26 = 2\left( {{m^2} + 5m} \right) + 26\\ = 2{\left( {m + \frac{5}{2}} \right)^2} + \frac{{27}}{2} \ge \frac{{27}}{2}\end{array}\)

Dấu ‘‘=’’ xảy ra \( \Leftrightarrow m + \frac{5}{2} = 0 \Leftrightarrow m =  - \frac{5}{2}\,\,\,\,\left( {tm} \right).\)

Vậy \(O{A^2} + O{B^2}\) đạt giá trị nhỏ nhất khi \(m =  - \frac{5}{2}.\)

Chọn A.

Lời giải chi tiết:

Phương pháp:

- Phương pháp vẽ đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)

     Bước 1: Vẽ đồ thị hàm số \(y = f\left( x \right).\)

     Bước 2: Giữ phần đồ thị nằm phía trên trục Ox, lấy đối xứng phần đồ thị nằm phía duới trục Ox qua trục Ox.

      Bước 3: Xóa đi phần đồ thị nằm phía dưới trục Ox.

- Số nghiệm của phương trình \(\left| {f\left( x \right)} \right| = m\) là số giao điểm của đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) và đường thẳng y = m song song với trục hoành.

Cách giải

Ta có đồ thị hàm số \(y = \left| {a{x^2} + bx + c} \right|\) và đường thẳng y = m như hình vẽ.

Dựa vào đồ thị hàm số ta thấy phương trình có 4 nghiệm phân biệt khi và chỉ khi 0 < m < 2.

Chọn đáp án C.

Phương pháp giải:

Lời giải chi tiết:

Đồ thị hàm số đi qua \(A\left( {2;0} \right) \Rightarrow 4a + 2b + c = 0\,\,\left( 1 \right)\).

Đồ thị hàm số đi qua \(B\left( { - 2; - 8} \right) \Rightarrow 4a - 2b + c =  - 8\,\,\left( 2 \right)\).

Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}4a + 2b + c = 0\\4a - 2b + c =  - 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + c =  - 4\\b = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c =  - 4a - 4\\b = 2\end{array} \right.\)

\( \Rightarrow \left( P \right):\,\,y = a{x^2} + 2x - 4a - 4\).

Hàm số có giá trị lớn nhất bằng \(1 \Rightarrow \left\{ \begin{array}{l}a < 0\\ - \dfrac{\Delta }{{4a}} = 1\end{array} \right.\).

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}a < 0\\ - \dfrac{{{2^2} - 4.a\left( { - 4a - 4} \right)}}{{4a}} = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a < 0\\4 + 16{a^2} + 16a =  - 4a\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a < 0\\16{a^2} + 20a + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\left[ \begin{array}{l}a =  - \dfrac{1}{4}\\a =  - 1\end{array} \right.\,\,\left( {tm} \right)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a =  - \dfrac{1}{4}\\a =  - 1\end{array} \right.\end{array}\)  

Với \(a =  - \dfrac{1}{4} \Rightarrow \left\{ \begin{array}{l}b = 2\\c =  - 3\end{array} \right. \Rightarrow {a^2} + {b^2} + {c^2} = \dfrac{{209}}{{16}}\)

Với \(a =  - 1 \Rightarrow \left\{ \begin{array}{l}b = 2\\c = 0\end{array} \right. \Rightarrow {a^2} + {b^2} + {c^2} = 5\)

Vậy \({a^2} + {b^2} + {c^2} = 5\) hoặc \({a^2} + {b^2} + {c^2} = \dfrac{{209}}{{16}}\).

Chọn D.

Lời giải chi tiết:

Hướng dẫn giải chi tiết

Dễ thấy rằng hai giao điểm có cùng tung độ và có hoành độ đối xứng với nhau qua trục đối xứng \(x = {{{m^2} + 1} \over 2}\)

Từ đây suy ra \(T = {x_1} + {x_2} = 2{{{m^2} + 1} \over 2} = {m^2} + 1 \ge 1\,\,\forall m\)

Suy ra \({T_{\min }} = {\left( {{x_1} + {x_2}} \right)_{\min }} = 1\) và đạt được khi \(m = 0\).

Chọn C.