Phương pháp giải:

Gọi \(M\left( {x;y} \right)\) thay và đẳng thức bài cho tìm mối quan hệ giữa \(x\) và \(y\).

Từ đó suy ra tập hợp điểm M.

Lời giải chi tiết:

Gọi \(M\left( {x;y} \right)\) ta có:

\(AM = \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 0} \right)}^2}} \) \( = \sqrt {{{\left( {x - 2} \right)}^2} + {y^2}} \)

\( \Rightarrow M{A^2} = A{M^2} = {\left( {x - 2} \right)^2} + {y^2}\)

\(BM = \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - 2} \right)}^2}} \) \( = \sqrt {{x^2} + {{\left( {y - 2} \right)}^2}} \)

\( \Rightarrow M{B^2} = B{M^2} = {x^2} + {\left( {y - 2} \right)^2}\)

Do đó ta có: \(M{A^2} + M{B^2} = 12\)

\(\begin{array}{l} \Leftrightarrow {\left( {x - 2} \right)^2} + {y^2} + {x^2} + {\left( {y - 2} \right)^2} = 12\\ \Leftrightarrow {x^2} - 4x + 4 + {y^2} + {x^2} + {y^2} - 4y + 4 = 12\\ \Leftrightarrow 2{x^2} + 2{y^2} - 4x - 4y - 4 = 0\\ \Leftrightarrow {x^2} + {y^2} - 2x - 2y - 2 = 0\end{array}\)

Dễ thấy, phương trình trên là phương trình đường tròn có tâm \(I\left( {1;1} \right)\) và bán kính \(R = \sqrt {{1^2} + {1^2} - \left( { - 2} \right)}  = 2\).

Vậy tập hợp điểm M thỏa mãn \(M{A^2} + M{B^2} = 12\) là đường tròn tâm \(I\left( {1;1} \right)\) và bán kính \(R = 2\).

Chọn D.

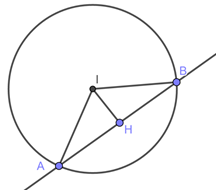
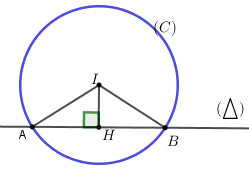
Phương pháp giải:

Bước 1: Gọi \(H\) là trung điểm dây \(AB \Rightarrow AH = HB = \frac{{AB}}{2}\) và \(IH \bot AB \Rightarrow IH = d\left( {I;d} \right)\)

Bước 2: Tính \({R^2} = A{I^2} = A{H^2} + I{H^2}\)(Áp dụng định lý Pithago trong tam giác vuông \(IAH\))

Bước 3: Lập phương trình đường tròn đi qua tâm \(I\) đã cho và bán kính \(R\) vừa tìm

Lời giải chi tiết:

Gọi \(H\) là trung điểm dây \(AB \Rightarrow AH = HB = \frac{{AB}}{2} = \frac{6}{2} = 3\) và \(IH \bot AB\)

\( \Rightarrow IH = d\left( {I;d} \right) = \frac{{\left| {3.\left( { - 1} \right) - 2 - 15} \right|}}{{\sqrt {{3^2} + {{\left( { - 1} \right)}^2}} }} = 2\sqrt {10} \)

Xét tam giác vuông \(IAH\)có: \(A{I^2} = I{H^2} + A{H^2} = {\left( {2\sqrt {10} } \right)^2} + {3^2} = 49\)

\( \Rightarrow {R^2} = 49\)

Phương trình đường tròn: \({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 49\)\( \Leftrightarrow {x^2} + {y^2} + 2x - 4y - 44 = 0\)

Chọn A.

Phương pháp giải:

Vì tâm của đường tròn nằm trên đường thẳng \(d:3x - y - 12 = 0\) nên ta gọi \(I\left( {a;\,\,3a - 12} \right)\) là tâm đường tròn.

Vì \(A,B\) nằm trên đường tròn nên \(IA = IB = R\) từ đó ta giải ra \(a \Rightarrow R\)

Lời giải chi tiết:

Vì tâm của đường tròn nằm trên đường thẳng \(d:3x - y - 12 = 0\) nên ta gọi \(I\left( {a;\,\,3a - 12} \right)\)là tâm đường tròn

Vì \(A,B\) nằm trên đường tròn nên ta có: \(IA = IB = R\)

\(\begin{array}{l} \Rightarrow I{A^2} = I{B^2} = {R^2}\\ \Leftrightarrow {\left( {a - 7} \right)^2} + {\left( {3a - 12 + 1} \right)^2} = {\left( {a - 1} \right)^2} + {\left( {3a - 12 - 5} \right)^2}\\ \Leftrightarrow {\left( {a - 7} \right)^2} + {\left( {3a - 11} \right)^2} = {\left( {a - 1} \right)^2} + {\left( {3a - 17} \right)^2}\\ \Leftrightarrow  - 14a + 49 - 66a + 121 =  - 2a + 1 - 102a + 289\\ \Leftrightarrow 24a = 120\\ \Leftrightarrow a = 5\\ \Rightarrow {R^2} = {\left( {5 - 7} \right)^2} + {\left( {3.5 - 11} \right)^2} = 20 \Rightarrow R = 2\sqrt 5 \end{array}\)

Chọn C.

Phương pháp giải:

+ Viết phương trình đường thẳng song song với đường thẳng \(d\).

+ Áp dụng CT tính khoảng cách .

Lời giải chi tiết:

Gọi \(d'\) là đường thẳng song song với \(d:\,\,3x + y - 2 = 0\).

\( \Rightarrow d':\,\,3x + y + m = 0\)

Gọi \(IH\) là khoảng cách từ \(I\) đến \(d'\), ta có:

 \(d\left( {I,\,\,d'} \right) = IH = \frac{{\left| { - 3 + 4 + m} \right|}}{5} = \frac{{\left| {m + 1} \right|}}{5}\)

Xét tam giác vuông \(IHB\) vuông tại \(H\) ta có: \(I{H^2} = I{B^2} - \left( {\frac{{A{B^2}}}{4}} \right) = 25 - 9 = 16\)

\( \Rightarrow \frac{{{{\left( {m + 1} \right)}^2}}}{{25}} = 16 \Leftrightarrow {\left( {m + 1} \right)^2} = 400 \Leftrightarrow \left| {m + 1} \right| = 20 \Rightarrow \left[ \begin{array}{l}m = 19\\m =  - 21\end{array} \right.\)

Với \(m = 19\), phương trình đường thẳng là \(d':3x + y + 19 = 0\)

Với \(m =  - 21\), phương trình đường thẳng là \(d':\,\,3x + y - 21 = 0\)

Chọn C.

Phương pháp giải:

+) Chứng minh đường thẳng \(\left( d \right)\) đi qua tâm \(I\)của đường tròn \(\left( C \right)\)

+) Đường tròn \(\left( C \right)\) nội tiếp hình vuông \(ABCD\) nên tọa độ điểm \(A\) là giao điểm của \(AI\) và hai tiếp tuyến của đường tròn \(\left( C \right)\)

Lời giải chi tiết:

Đường tròn \(\left( C \right):{x^2} + {y^2} - 8x + 6y + 21 = 0 \Rightarrow \left\{ \begin{array}{l}I\left( {4;\,\, - 3} \right)\\R = 2\end{array} \right.\)

Thay \(I\left( {4;\,\, - 3} \right)\) vào phương trình \(d:x + y - 1 = 0\) ta được: \(4 + \left( { - 3} \right) - 1 = 0\)

\( \Rightarrow I\left( {4;\,\, - 3} \right) \in d\)

Vì \(A \in d\) và \(I \in d\) nên \(AI\) là đường chéo của hình vuông ngoại tiếp đường tròn có bán kính \(R = 2.\)

Vậy \(AI\) là một đường chéo của hình vuông ngoại tiếp đường tròn, có bán kính \(R = 2\); \(x = 2\) và \(x = 6\) là \(2\) tiếp tuyến của \(\left( C \right)\)  nên ta có:

Trường hợp \(1\): \(A\) là giao điểm các đường \(d\) và \(x = 2 \Rightarrow A\left( {2;\,\, - 1} \right)\)

Trường hợp \(2\): \(A\) là giao điểm các đường \(d\) và \(x = 6 \Rightarrow A\left( {6;\,\, - 5} \right)\)

Vậy \(A\left( {2;\,\, - 1} \right)\) và \(A\left( {6;\,\, - 5} \right)\).

Chọn  D

Phương pháp giải:

Xác định tâm \(I\)và bán kính \(R\) của đường tròn \(\left( C \right)\).

+) Nếu \(I \in \left( \Delta  \right)\) thì độ dài dây cung bằng đường kính của đường tròn \(\left( C \right)\).

+) Nếu \(I \notin \left( \Delta  \right)\) thì xác định tọa độ giao điểm của \(\left( \Delta  \right)\) và \(\left( C \right)\).

Lời giải chi tiết:

Cách 1: Đường tròn \(\left( C \right):\,\,{(x - a)^2} + {(y - b)^2} = {R^2}\) có tâm \(I\left( {a;\,\,b} \right)\) và bán kính \(R\).

Vì \(a + b - a - b = 0\) nên điểm \(I\left( {a;\,\,b} \right)\) thuộc đường thẳng \(\left( d \right)\)

Suy ra, đường tròn \(\left( C \right)\) cắt đường thẳng \(\left( d \right)\) theo một dây cung có độ dài bằng đường kính \( = 2R\).

Cách 2:

Tọa độ giao điểm của \(\left( C \right)\) và \(\left( d \right)\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\\x + y - a - b = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\\y = a + b - x\end{array} \right.\)

\( \Rightarrow {\left( {x - a} \right)^2} + {\left( {x - a} \right)^2} = {R^2} \Leftrightarrow \left[ \begin{array}{l}x = a + \frac{R}{{\sqrt 2 }} \Rightarrow y = b - \frac{R}{{\sqrt 2 }}\\x = a - \frac{R}{{\sqrt 2 }} \Rightarrow y = b + \frac{R}{{\sqrt 2 }}\end{array} \right.\)

Vậy tọa độ giao điểm của \(\left( C \right)\) và \(\left( d \right)\) là \(A\left( {a + \frac{R}{{\sqrt 2 }};\,\,b - \frac{R}{{\sqrt 2 }}} \right)\) và \(B\left( {a - \frac{R}{{\sqrt 2 }};\,\,b + \frac{R}{{\sqrt 2 }}} \right)\).

\(AB = \sqrt {{{\left( {a - \frac{R}{{\sqrt 2 }} - a - \frac{R}{{\sqrt 2 }}} \right)}^2} + {{\left( {b + \frac{R}{{\sqrt 2 }} - b + \frac{R}{{\sqrt 2 }}} \right)}^2}}  = \sqrt {{{\left( { - \frac{{2R}}{{\sqrt 2 }}} \right)}^2} + {{\left( { - \frac{{2R}}{{\sqrt 2 }}} \right)}^2}}  = \sqrt {2 \cdot \frac{{4{R^2}}}{2}}  = \sqrt {4{R^2}}  = 2R\)

Vậy \(AB = 2R\).

Chọn  A

Phương pháp giải:

Xác định tọa độ của hai điểm \(M\) và \(N\).

Lời giải chi tiết:

Ta có: \(M \in d \Rightarrow M\left( {3b + 4;\,\,b} \right)\)

Vì \(N\) đối xứng với \(M\) qua \(A\left( {3;\,\,1} \right)\) suy ra \(N\left( {2 - 3b;\,\,2 - b} \right)\).

Mặt khác, \(N \in \left( C \right)\) nên ta có: \({\left( {2 - 3b} \right)^2} + {\left( {2 - b} \right)^2} - 4\left( {2 - b} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}b = 0\\b = \frac{6}{5}\end{array} \right.\)

+) Với \(b = 0 \Rightarrow M\left( {4;\,\,0} \right)\) và \(N\left( {2;\,\,2} \right)\)\( \Rightarrow MN = \sqrt {{{\left( {2 - 4} \right)}^2} + {{\left( {2 - 0} \right)}^2}}  = \sqrt {{2^2} + {2^2}}  = 2\sqrt 2 \)

+) Với \(b = \frac{6}{5} \Rightarrow M\left( {\frac{{38}}{5};\,\,\frac{6}{5}} \right)\) và \(N\left( { - \frac{8}{5};\,\,\frac{4}{5}} \right) \Rightarrow MN = \sqrt {{{\left( { - \frac{8}{5} - \frac{{38}}{5}} \right)}^2} + {{\left( {\frac{4}{5} - \frac{6}{5}} \right)}^2}}  = \sqrt {\frac{{6088}}{{25}}} \)

Vậy \(MN = 2\sqrt 2 \) và \(MN = \sqrt {\frac{{6088}}{{25}}} \).

Chọn  B

Phương pháp giải:

+) Viết phương trình tổng quát của đường thẳng \(\left( d \right)\).

+) Xác định khoảng cách từ điểm \(I\) đến đường thẳng \(\left( \Delta  \right)\) và sau đó tìm \(m\).

Lời giải chi tiết:

Ta có: \(\left( C \right):\,\,{\left( {x + 4} \right)^2} + {\left( {y - 3} \right)^2} = 25 \Rightarrow \left\{ \begin{array}{l}I\left( { - 4;\,\,3} \right)\\R = 5\end{array} \right.\)

Gọi \(H\) là trung điểm \(AB\), \(AH = 3\).

Do \(d \bot \Delta \) nên phương trình của \(d\) có dạng: \(4x + 3y + m = 0\)

Ta có: \(d\left( {I,\,\,\left( \Delta  \right)} \right) = IH = \sqrt {A{I^2} - A{H^2}}  = \sqrt {{5^2} - {3^2}}  = 4\)

\( \Rightarrow \frac{{\left| {4.\left( { - 4} \right) + 3.3 + m} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 4\)\( \Leftrightarrow \frac{{\left| { - 16 + 9 + m} \right|}}{5} = 4 \Leftrightarrow \left| { - 7 + m} \right| = 20 \Leftrightarrow \left[ \begin{array}{l} - 7 + m = 20\\ - 7 + m =  - 20\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 27\\m =  - 13\end{array} \right.\)

Với \(m = 27\) suy ra \(d:\,\,4x + 3y + 27 = 0\)

Với \(m =  - 13\) suy ra \(d:\,\,4x + 3y - 13 = 0\)

Vậy \(d:\,\,4x + 3y + 27 = 0\) hoặc \(d:\,\,4x + 3y - 13 = 0\).

Chọn  D

Phương pháp giải:

Để đường thẳng \(\left( d \right)\) cắt đường tròn \(\left( C \right)\) tại hai điểm phân biệt \(A\) và \(B\) thì \(d\left( {I,\,\,\left( d \right)} \right) < R\).

Lời giải chi tiết:

\(\left( C \right):\,\,{x^2} + {y^2} - 2x + 4y - 4 = 0 \Rightarrow \left\{ \begin{array}{l}I\left( {1;\,\, - 2} \right)\\R = 3\end{array} \right.\)

\(\left( d \right)\) cắt \(\left( C \right)\) tại hai điểm phân biệt \(A\) và \(B\)\( \Leftrightarrow d\left( {I,\,\,\left( d \right)} \right) < R\)

\( \Leftrightarrow \left| {\sqrt 2  - 2m + 1 - \sqrt 2 } \right| < 3\sqrt {2 + {m^2}} \)

\( \Leftrightarrow 1 - 4m + 4{m^2} < 18 + 9{m^2}\)

\( \Leftrightarrow 5{m^2} + 4m + 17 > 0\)

\( \Leftrightarrow 5.\left( {{m^2} + 2 \cdot m \cdot \frac{2}{5} + \frac{4}{5}} \right) + 13 > 0\)

\( \Leftrightarrow 5.{\left( {m + \frac{2}{5}} \right)^2} + 13 > 0\) luôn đúng với \(\forall m\)

Vậy \(m \in \mathbb{R}.\)

Chọn  C

Phương pháp giải:

Đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 1} \right)\) và bán kính \(R = \sqrt {10} .\)

Giả sử tiếp tuyến \(\Delta :\,\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right).\)

\(\Delta \) là tiếp tuyến của \(\left( C \right) \Rightarrow d\left( {I;\,\,\Delta } \right) = R = \sqrt {10} .\)

Theo đề bài ta có: \(\Delta \) tạo với \(d\) một góc \({45^0} \Rightarrow \cos {45^0} = \frac{{\left| {\overrightarrow {{n_\Delta }} .\overrightarrow {{n_d}} } \right|}}{{\left| {\overrightarrow {{n_\Delta }} } \right|.\left| {\overrightarrow {{n_d}} } \right|}}.\)

Giải phương trình để từ đó lập phương trình đường thẳng \(\Delta .\)

Lời giải chi tiết:

Ta có: \(\overrightarrow {{n_d}}  = \left( {2;\,\,1} \right).\)

Đường tròn \(\left( C \right)\) có tâm \(I\left( {1; - 1} \right)\) và bán kính \(R = \sqrt {10} .\)

Giả sử tiếp tuyến \(\Delta :\,\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right) \Rightarrow \overrightarrow {{n_\Delta }}  = \left( {a;\,\,b} \right).\)

\(\Delta \) là tiếp tuyến của \(\left( C \right) \Rightarrow d\left( {I;\,\,\Delta } \right) = R = \sqrt {10} .\)

\( \Leftrightarrow \frac{{\left| {a - b + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \sqrt {10}  \Leftrightarrow \left| {a - b + c} \right| = \sqrt {10\left( {{a^2} + {b^2}} \right)} \,\,\,\,\left( 1 \right)\)

Theo đề bài ta có: \(\Delta \) tạo với \(d\) một góc \({45^0} \Rightarrow \cos {45^0} = \frac{{\left| {\overrightarrow {{n_\Delta }} .\overrightarrow {{n_d}} } \right|}}{{\left| {\overrightarrow {{n_\Delta }} } \right|.\left| {\overrightarrow {{n_d}} } \right|}}\)

\(\begin{array}{l} \Leftrightarrow \frac{{\left| {2a + b} \right|}}{{\sqrt {{2^2} + 1} .\sqrt {{a^2} + {b^2}} }} = \frac{{\sqrt 2 }}{2}\\ \Leftrightarrow 2\left| {2a + b} \right| = \sqrt {10} .\sqrt {{a^2} + {b^2}}  \Leftrightarrow 4{\left( {2a + b} \right)^2} = 10\left( {{a^2} + {b^2}} \right)\\ \Leftrightarrow 6{a^2} + 16ab - 6{b^2} = 0 \Leftrightarrow 3{a^2} + 8ab - 3{b^2} = 0\\ \Leftrightarrow \left( {a + 3b} \right)\left( {3a - b} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}a + 3b = 0\\3a - b = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a =  - 3b\\a = \frac{b}{3}\end{array} \right.\end{array}\)

+) Với \(a =  - 3b \Rightarrow \left( 1 \right) \Leftrightarrow \left| { - 3b - b + c} \right| = \sqrt {10\left( {9{b^2} + {b^2}} \right)} \)

\(\begin{array}{l} \Leftrightarrow \left| {c - 4b} \right| = \sqrt {100{b^2}}  \Leftrightarrow \left| {c - 4b} \right| = 10\left| b \right|\\ \Leftrightarrow \left[ \begin{array}{l}c - 4b = 10b\\c - 4b =  - 10b\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}c = 14b\\c =  - 6b\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a =  - 3b\\c = 14b\end{array} \right. \Rightarrow {\Delta _1}:\,\,\, - 3x + y + 14 = 0\\\left\{ \begin{array}{l}a =  - 3b\\c =  - 6b\end{array} \right. \Rightarrow {\Delta _2}:\,\, - 3x + y - 6 = 0\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}{\Delta _1}:\,\,\,3x - y - 14 = 0\\{\Delta _2}:\,\,3x - y + 6 = 0\end{array} \right..\end{array}\)

+) Với \(a = \frac{b}{3} \Rightarrow \left( 1 \right) \Leftrightarrow \left| {\frac{b}{3} - b + c} \right| = \sqrt {10\left( {\frac{{{b^2}}}{9} + {b^2}} \right)} \)

\(\begin{array}{l} \Leftrightarrow \left| {c - \frac{{2b}}{3}} \right| = \sqrt {\frac{{100{b^2}}}{9}}  \Leftrightarrow \left| {c - \frac{{2b}}{3}} \right| = \frac{{10}}{3}\left| b \right|\\ \Leftrightarrow \left[ \begin{array}{l}c - \frac{{2b}}{3} = \frac{{10b}}{3}\\c - \frac{{2b}}{3} =  - \frac{{10b}}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}c = 4b\\c =  - \frac{8}{3}b\end{array} \right.\end{array}\)

\( \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = \frac{b}{3}\\c = 4b\end{array} \right. \Rightarrow {\Delta _3}:\,\,\,\frac{1}{3}x + y + 4 = 0\\\left\{ \begin{array}{l}a = \frac{b}{3}\\c =  - \frac{{8b}}{3}\end{array} \right. \Rightarrow {\Delta _4}:\,\,\frac{1}{3}x + y - \frac{8}{3} = 0\end{array} \right.\)

\( \Rightarrow \left[ \begin{array}{l}{\Delta _3}:\,\,\,x + 3y + 12 = 0\\{\Delta _4}:\,\,x + 3y - 8 = 0\end{array} \right..\)

Như vậy có 4 tiếp tuyến thỏa mãn bài toán.

Chọn  A.

Phương pháp giải:

Xác định tâm, tính bán kính các đường tròn và vị trí tương đối của hai đường tròn.

+) Nếu hai đường tròn tiếp xúc trong nhau thì có 1 đường tiếp tuyến chung.

+) Nếu hai đường tròn tiếp xúc ngoài nhau thì có 3 đường tiếp tuyến chung.

+) Nếu hai đường tròn ngoài nhau thì có 4 đường tiếp tuyến chung.

+) Nếu hai đường tròn đựng nhau thì không có tiếp tuyến chung.

+) Nếu hai đường tròn cắt nhau thì có 2 đường tiếp tuyến chung.

Gọi \(\Delta :\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\) là tiếp tuyến chung của hai đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\)

Khi đó ta có: \(\left\{ \begin{array}{l}d\left( {{I_1};\,\,\Delta } \right) = {R_1}\\d\left( {{I_2};\,\,\Delta } \right) = {R_2}\end{array} \right..\)

Lời giải chi tiết:

Ta có:

\(\left( {{C_1}} \right):\,\,\,{x^2} + {y^2} - 2x - 3 = 0\) có tâm \({I_1}\left( {1;\,\,0} \right)\) và bán kính \({R_1} = \sqrt {1 + 3}  = 2.\)

\(\left( {{C_2}} \right):\,\,{x^2} + {y^2} - 8x - 8y + 28 = 0\) có tâm \({I_2}\left( {4;\,\,4} \right)\) và bán kính \({R_2} = \sqrt {{4^2} + {4^2} - 28}  = 2.\)

\( \Rightarrow \overrightarrow {{I_1}{I_2}}  = \left( {3;\,\,4} \right) \Rightarrow {I_1}{I_2} = 5.\)

Lại có:\({R_1} + {R_2} = 2 + 2 = 4.\)

\( \Rightarrow {I_1}{I_2} = 5 > {R_1} + {R_2} = 4 \Rightarrow \left( {{C_1}} \right)\)  và \(\left( {{C_2}} \right)\) ngoài nhau.

\( \Rightarrow \) Hai đường tròn có 4 tiếp tuyến chung.

Gọi \(\Delta :\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\) là tiếp tuyến chung của hai đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\)

Khi đó ta có: \(\left\{ \begin{array}{l}d\left( {{I_1};\,\,\Delta } \right) = {R_1}\\d\left( {{I_2};\,\,\Delta } \right) = {R_2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}\frac{{\left| {a + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 2\\\frac{{\left| {4a + 4b + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left| {a + c} \right| = 2\sqrt {{a^2} + {b^2}} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\\left| {4a + 4b + c} \right| = 2\sqrt {{a^2} + {b^2}} \,\,\,\,\left( 2 \right)\end{array} \right.\)

\( \Rightarrow \left| {a + c} \right| = \left| {4a + 4b + c} \right| \Leftrightarrow \left[ \begin{array}{l}a + c = 4a + 4b + c\\a + c =  - 4a - 4b - c\end{array} \right.\)  \( \Leftrightarrow \left[ \begin{array}{l}3a + 4b = 0\\5a + 4b + 2c = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a =  - \frac{{4b}}{3}\\c =  - \frac{{5a + 4b}}{2}\end{array} \right..\)

+) Với \(a =  - \frac{{4b}}{3}\) \( \Rightarrow \left| {c - \frac{{4b}}{3}} \right| = 2\sqrt {\frac{{16}}{9}{b^2} + {b^2}} \) \( \Leftrightarrow \left| {c - \frac{{4b}}{3}} \right| = \frac{{10\left| b \right|}}{3}\)

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}c - \frac{{4b}}{3} = \frac{{10b}}{3}\\c - \frac{{4b}}{3} =  - \frac{{10b}}{3}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}c = \frac{{14b}}{3}\\c =  - 2b\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a =  - \frac{{4b}}{3}\\c = \frac{{14b}}{3}\end{array} \right.\\\left\{ \begin{array}{l}a =  - \frac{{4b}}{3}\\c =  - 2b\end{array} \right.\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}{\Delta _1}:\,\,\, - \frac{4}{3}x + y + \frac{{14}}{3} = 0\\{\Delta _2}:\,\, - \frac{4}{3}x + y - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{\Delta _1}:\,\,\,\,4x - 3y - 14 = 0\\{\Delta _2}:\,\,\,4x - 3y + 6 = 0\end{array} \right.\end{array}\)

+) Với \(c =  - \frac{{5a + 4b}}{2}\) \( \Rightarrow \left( 1 \right) \Leftrightarrow \left| {a - \frac{{5a - 4b}}{2}} \right| = 2\sqrt {{a^2} + {b^2}} \)

\(\begin{array}{l} \Leftrightarrow \left| {3a + 4b} \right| = 4\sqrt {{a^2} + {b^2}}  \Leftrightarrow {\left( {3a + 4b} \right)^2} = 16\left( {{a^2} + {b^2}} \right)\\ \Leftrightarrow 9{a^2} + 24ab + 16{b^2} = 16{a^2} + 16{b^2}\\ \Leftrightarrow a\left( {7a - 24b} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\7a - 24b = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 0 \Rightarrow c =  - 2b\\a = \frac{{24b}}{7} \Rightarrow c =  - \frac{{74b}}{7}\end{array} \right.\end{array}\)

\(\begin{array}{l} \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = 0\\c =  - 2b\end{array} \right.\\\left\{ \begin{array}{l}a = \frac{{24b}}{7}\\c =  - \frac{{74b}}{7}\end{array} \right.\end{array} \right. \Rightarrow \left[ \begin{array}{l}{\Delta _3}:\,\,\,y - 2 = 0\\{\Delta _4}:\,\,\,\frac{{24}}{7}x + y - \frac{{74}}{7} = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{\Delta _3}:\,\,y - 2 = 0\\{\Delta _4}:\,\,24x + 7y - 74 = 0\end{array} \right..\end{array}\)

Vậy có 4 đường tiếp tuyến thỏa mãn bài toán là: \(\left[ \begin{array}{l}{\Delta _1}:\,\,\,4x - 3y - 14 = 0\\{\Delta _2}:\,\,\,4x - 3y + 6 = 0\\{\Delta _3}:\,\,y - 2 = 0\\{\Delta _4}:\,\,24x + 7y - 74 = 0\end{array} \right..\)

Chọn B.

Phương pháp giải:

+) Viết phương trình đường thẳng \(\left( \Delta  \right)\) đi qua hai điểm \(B\) và \(C\).

+) Xác định tọa độ giao điểm của đường thẳng \(\left( \Delta  \right)\)với \(\left( C \right)\).

Lời giải chi tiết:

\(\left( C \right):\,\,{x^2} + {y^2} - 2x - 4y - 5 = 0 \Rightarrow \left\{ \begin{array}{l}I\left( {1;2} \right)\\R = \sqrt {10} \end{array} \right.\)

Để \(\Delta ABC\) đều thì \(I\) là trọng tâm của tam giác \(ABC\).

\(A\left( {0;\,\, - 1} \right),\,\,I\left( {1;\,\,2} \right) \Rightarrow \overrightarrow {AI}  = \left( {1;\,\,3} \right)\)

Gọi \(H\) là trung điểm của \(BC\). Suy ra, \(\overrightarrow {AI}  = 2\,.\,\overrightarrow {IH}  \Rightarrow H\left( {\frac{3}{2};\,\,\frac{7}{2}} \right)\).

Ta có:

\(\left( {BC} \right):\left\{ \begin{array}{l}{\mathop{\rm qua}\nolimits} \,H\left( {\frac{3}{2};\frac{7}{2}} \right)\\{{\vec n}_{BC}} = \overrightarrow {AI}  = \left( {1;\,\,3} \right)\end{array} \right. \Rightarrow \left( {BC} \right):\,\,1\,\,.\,\,\left( {x - \frac{3}{2}} \right) + 3\,\,.\,\,\left( {y - \frac{7}{2}} \right) = 0\)\( \Rightarrow \left( {BC} \right):\,\,x + 3y - 12 = 0\)

Vì \(B,\,\,C \in \left( C \right)\) nên tọa độ của \(B\) và \(C\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}{x^2} + {y^2} - 2x - 4y - 5 = 0\\x + 3y - 12 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} - 2x - 4y - 5 = 0\\x = 12 - 3y\end{array} \right.\)

\( \Rightarrow {\left( {12 - 3y} \right)^2} + {y^2} - 2\left( {12 - 3y} \right) - 4y - 5 = 0\)

\( \Leftrightarrow 144 - 72y + 9{y^2} + {y^2} - 24 + 6y - 4y - 5 = 0\)

\( \Leftrightarrow 10{y^2} - 70y + 115 = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}y = \frac{{3 - 3\sqrt 3 }}{2} \Rightarrow x = \frac{{7 + \sqrt 3 }}{2}\\y = \frac{{3 + 3\sqrt 3 }}{2} \Rightarrow x = \frac{{7 - \sqrt 3 }}{2}\end{array} \right.\)

Vậy \(B\left( {\frac{{7 + \sqrt 3 }}{2};\,\,\frac{{3 - 3\sqrt 3 }}{2}} \right),\,\,C\left( {\frac{{7 - \sqrt 3 }}{2};\,\,\frac{{3 + 3\sqrt 3 }}{2}} \right)\,\) hoặc \(B\left( {\frac{{7 - \sqrt 3 }}{2};\,\,\frac{{3 + 3\sqrt 3 }}{2}} \right),\,\,C\left( {\frac{{7 + \sqrt 3 }}{2};\,\,\frac{{3 - 3\sqrt 3 }}{2}} \right)\,\).

Chọn  A

Phương pháp giải:

Đường tròn \(\left( C \right)\) có tâm \(I\left( {0;\,\,0} \right)\) và bán kính \(R = 5.\)

Giả sử tiếp tuyến \(d:\,\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right).\)

\(d\) là tiếp tuyến của \(\left( C \right) \Rightarrow d\left( {I;\,\,d} \right) = R = 5.\)

Theo đề bài ta có: \(d\) tạo với \(\Delta \) một góc \(\alpha  \Rightarrow \cos \alpha  = \frac{{\left| {\overrightarrow {{n_\Delta }} .\overrightarrow {{n_d}} } \right|}}{{\left| {\overrightarrow {{n_\Delta }} } \right|.\left| {\overrightarrow {{n_d}} } \right|}}.\)

Giải phương trình để từ đó lập phương trình đường thẳng \(d.\)

Lời giải chi tiết:

Ta có: \(\overrightarrow {{n_\Delta }}  = \left( {1;\,\,2} \right).\) Đường tròn \(\left( C \right)\) có tâm \(I\left( {0;\,\,0} \right)\) và bán kính \(R = 5.\)

Giả sử tiếp tuyến \(d:\,\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right) \Rightarrow \overrightarrow {{n_d}}  = \left( {a;\,\,b} \right)\)

\(d\) là tiếp tuyến của \(\left( C \right) \Rightarrow d\left( {I;\,\,d} \right) = R = 5.\)

\( \Rightarrow \frac{{\left| c \right|}}{{\sqrt {{a^2} + {b^2}} }} = 5 \Leftrightarrow \left| c \right| = 5\sqrt {{a^2} + {b^2}} \,\,\,\,\left( * \right)\)

Theo đề bài ta có: \(d\) tạo với \(\Delta \) một góc \(\alpha  \Rightarrow \cos \alpha  = \frac{{\left| {\overrightarrow {{n_\Delta }} .\overrightarrow {{n_d}} } \right|}}{{\left| {\overrightarrow {{n_\Delta }} } \right|.\left| {\overrightarrow {{n_d}} } \right|}}.\)

\(\begin{array}{l} \Rightarrow \frac{2}{{\sqrt 5 }} = \frac{{\left| {a + 2b} \right|}}{{\sqrt 5 .\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \left| {a + 2b} \right| = 2\sqrt {{a^2} + {b^2}} \\ \Leftrightarrow {\left( {a + 2b} \right)^2} = 4{a^2} + 4{b^2} \Leftrightarrow 3{a^2} - 4ab = 0\\ \Leftrightarrow a\left( {3a - 4b} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\3a - 4b = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 0\\b = \frac{{3a}}{4}\end{array} \right..\end{array}\)

+) Với \(a = 0 \Rightarrow \overrightarrow {{n_d}}  = \left( {0;\,\,b} \right)\) \( \Rightarrow d:\,\,\,by + c = 0.\)

\( \Rightarrow \left( * \right) \Leftrightarrow \left| c \right| = 5\sqrt {{b^2}}  \Leftrightarrow \left| c \right| = 5\left| b \right|\)

\( \Leftrightarrow \left[ \begin{array}{l}c = 5b\\c =  - 5b\end{array} \right. \Rightarrow \left[ \begin{array}{l}{d_1}:\,\,\,y + 5 = 0\\{d_2}:\,\,\,y - 5 = 0\,\,\,\end{array} \right.\)

+) Với \(b = \frac{{3a}}{4} \Rightarrow \overrightarrow {{n_d}}  = \left( {a;\,\frac{{3a}}{4}} \right) = \frac{a}{4}\left( {4;\,\,3} \right)\)

\(\begin{array}{l} \Rightarrow \left( * \right) \Leftrightarrow \left| c \right| = 5\sqrt {{a^2} + \frac{{9{a^2}}}{{16}}}  \Leftrightarrow \left| c \right| = \frac{{25}}{4}\left| a \right|\\ \Leftrightarrow \left[ \begin{array}{l}c = \frac{{25a}}{4}\\c =  - \frac{{25a}}{4}\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}b = \frac{{3a}}{4}\\c = \frac{{25a}}{4}\end{array} \right.\\\left\{ \begin{array}{l}b = \frac{{3a}}{4}\\c =  - \frac{{25a}}{4}\end{array} \right.\end{array} \right. \Rightarrow \left[ \begin{array}{l}{d_3}:\,\,\,x + \frac{3}{4}y + \frac{{25}}{4} = 0\\{d_4}:\,\,\,x + \frac{3}{4}y - \frac{{25}}{4} = 0\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}{d_3}:\,\,\,4x + 3y + 25 = 0\\{d_4}:\,\,\,4x + 3y - 25 = 0\end{array} \right..\end{array}\)

Vậy có 4 tiếp tuyến thỏa mãn bài toán: \(\left[ \begin{array}{l}{d_1}:\,\,\,y + 5 = 0\\{d_2}:\,\,\,y - 5 = 0\\{d_3}:\,\,\,4x + 3y + 25 = 0\\{d_4}:\,\,\,4x + 3y - 25 = 0\end{array} \right..\)

Chọn D.

Phương pháp giải:

+) Đường tròn \(\left( C \right)\) có tâm \(I\)cắt \(\left( d \right)\) tại hai điểm phân biệt \(A\) và \(B\) thì \(d\left( {I,\,\,\left( d \right)} \right) < R\).

+) Áp dụng CT tính diện tích tam giác.

Lời giải chi tiết:

\(\left( C \right):\,\,{x^2} + {y^2} = 1 \Rightarrow \left\{ \begin{array}{l}O\left( {0;\,\,0} \right)\\R = 1\end{array} \right.\)

Vì \(\left( d \right)\) cắt \(\left( C \right)\) tại hai điểm phân biệt \(A\) và \(B\) nên \(d\left( {O;\,\,d} \right) < R \Rightarrow d\left( {O;\,\,d} \right) < 1\).

Ta có: \({S_{OAB}} = \frac{1}{2} \cdot OA \cdot OB \cdot \sin \widehat {AOB} = \frac{1}{2} \cdot \sin \widehat {AOB} \le \frac{1}{2}\)

Dấu “\( = \)” xảy ra khi \(\widehat {AOB} = {90^0}\).

\( \Rightarrow {S_{\Delta OAB}}\) lớn nhất \( \Leftrightarrow \widehat {AOB} = {90^0}\).

\( \Rightarrow \Delta OAB\) là tam giác vuông cân tại \(O\).

\( \Rightarrow d\left( {O;\,\,d} \right) = \frac{{\left| {1\,\,.\,\,0 + 1\,\,.\,\,0 + m} \right|}}{{\sqrt {{1^2} + {1^2}} }} = \frac{{\left| m \right|}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }} \Rightarrow \left| m \right| = 1 \Rightarrow \left[ \begin{array}{l}m = 1\\m =  - 1\end{array} \right.\)

Vậy \(m =  \pm 1\).

Chọn  C

Phương pháp giải:

Đường tròn \(\left( C \right):\,\,{x^2} + {y^2} + 2x - 4y - 4 = 0\) có tâm \(I\left( { - 1;\,\,2} \right)\) và bán kính \(R = 3.\)

Ta có: \(\overrightarrow {IA}  = \left( {3;\,\,3} \right) \Rightarrow IA = 3\sqrt 2  > R \Rightarrow A\)  nằm ngoài đường tròn \(\left( C \right).\)

Từ đó suy ra phương trình các đường tiếp tuyến của đường tròn \(\left( C \right)\) và tìm tọa độ các điểm \(M,\,\,N \Rightarrow MN.\)

Lời giải chi tiết:

Đường tròn \(\left( C \right):\,\,{x^2} + {y^2} + 2x - 4y - 4 = 0\) có tâm \(I\left( { - 1;\,\,2} \right)\) và bán kính \(R = 3.\)

Ta có: \(\overrightarrow {IA}  = \left( {3;\,\,3} \right) \Rightarrow IA = 3\sqrt 2  > R \Rightarrow A\)  nằm ngoài đường tròn \(\left( C \right).\)

\( \Rightarrow \) Từ \(A\) có thể kẻ được 2 đường tiếp tuyến với đường tròn \(\left( C \right).\)

Gọi tiếp tuyến của đường tròn \(\left( C \right)\) kẻ từ \(A\left( {2;\,5} \right)\) và có VTPT là \(\overrightarrow n  = \left( {a;\,\,b} \right).\) 

\(\begin{array}{l} \Rightarrow d:\,\,\,a\left( {x - 2} \right) + b\left( {y - 5} \right) = 0\\ \Rightarrow d:\,\,\,ax + by - 2a - 5b = 0\end{array}\)

\(\begin{array}{l} \Rightarrow d\left( {I;\,\,d} \right) = R \Leftrightarrow \frac{{\left| { - a + 2b - 2a - 5b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 3\\ \Leftrightarrow \left| { - 3a - 3b} \right| = 3\sqrt {{a^2} + {b^2}} \\ \Leftrightarrow \left| {a + b} \right| = \sqrt {{a^2} + {b^2}} \\ \Leftrightarrow {a^2} + {b^2} + 2ab = {a^2} + {b^2}\\ \Leftrightarrow ab = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0 \Rightarrow {d_1}:\,\,\,\,y - 5 = 0\\b = 0 \Rightarrow {d_2}:\,\,\,x - 2 = 0\end{array} \right..\end{array}\)

Vậy có hai tiếp tuyến là \({d_1}:\,\,\,y = 5\) và \({d_2}:\,\,x = 2.\)

Gọi \(M = {d_1} \cap \left( C \right) \Rightarrow \) Tọa độ điểm \(M\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}y = 5\\{x^2} + {y^2} - 2x - 6y + 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 5\\x =  - 1\end{array} \right. \Rightarrow M\left( { - 1;\,\,5} \right).\)

Gọi \(N = {d_2} \cap \left( C \right) \Rightarrow \) Tọa độ điểm \(N\) là nghiệm của hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}x = 2\\{x^2} + {y^2} - 2x - 6y + 6 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right. \Rightarrow N\left( {2;\,\,2} \right).\\ \Rightarrow MN = \sqrt {{{\left( {2 + 1} \right)}^2} + {{\left( {2 - 5} \right)}^2}}  = 3\sqrt 2 .\end{array}\)

Chọn  A.

Phương pháp giải:

Đường tròn \(\left( C \right):\,\,\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\) có tâm \(I\left( {1;\, - 2} \right)\) và bán kính \(R = 3.\)

\(\Delta PAB\) là tam giác đều \( \Leftrightarrow PA = 2AI = 6.\)

\( \Rightarrow P \in \left( {C'} \right)\) với \(\left( {C'} \right)\) là đường tròn tâm \(I\left( {1; - 2} \right)\) và có bán kính \(R' = 6cm.\)

\( \Rightarrow \) \(P\) là giao điểm của \(d:\,\,\,3x - 4y + m = 0\) và \(\left( {C'} \right).\)

Mà có duy nhất một điểm \(P\) mà từ \(P\) có thể kẻ được hai tiếp tuyến \(PA,\,\,PB\) với \(A,\,\,B\) là các tiếp điểm sao cho \(\Delta PAB\) là tam giác đều. 

\( \Rightarrow d\) tiếp xúc với \(\left( {C'} \right)\) hay \(d'\) là tiếp tuyến của \(\left( {C'} \right)\) tại \(P.\)

\( \Rightarrow d\left( {I;\,\,d} \right) = 6.\)

Lời giải chi tiết:

Đường tròn \(\left( C \right):\,\,\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 9\) có tâm \(I\left( {1;\, - 2} \right)\) và bán kính \(R = 3.\)

\(\Delta PAB\) là tam giác đều \( \Leftrightarrow PI = 2AI = 6.\)

\( \Rightarrow P \in \left( {C'} \right)\) với \(\left( {C'} \right)\) là đường tròn tâm \(I\left( {1; - 2} \right)\) và có bán kính \(R' = 6cm.\)

\( \Rightarrow \left( {C'} \right):\,\,\,\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 36.\)

\( \Rightarrow \) \(P\) là giao điểm của \(d:\,\,\,3x - 4y + m = 0\) và \(\left( {C'} \right).\)

Mà có duy nhất một điểm \(P\) mà từ \(P\) có thể kẻ được hai tiếp tuyến \(PA,\,\,PB\) với \(A,\,\,B\) là các tiếp điểm sao cho \(\Delta PAB\) là tam giác đều. 

\( \Rightarrow d\) tiếp xúc với \(\left( {C'} \right)\) hay \(d'\) là tiếp tuyến của \(\left( {C'} \right)\) tại \(P.\)

\(\begin{array}{l} \Rightarrow d\left( {I;\,\,d} \right) = 6 \Leftrightarrow \frac{{\left| {3 + 4.2 + m} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 6\\ \Leftrightarrow \left| {11 + m} \right| = 30 \Leftrightarrow \left[ \begin{array}{l}m + 11 = 30\\m + 11 =  - 30\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 19\\m =  - 41\end{array} \right..\end{array}\)

Chọn  D.

Phương pháp giải:

Đường tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {5;\,\,0} \right)\) và bán kính \({R_1} = 5.\) 

Đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( { - 2;\,\,1} \right)\) và bán kính \({R_2} = \sqrt {{2^2} + 1 + 20}  = 5.\) 

\( \Rightarrow {I_1}{I_2} = \sqrt {{{\left( { - 2 - 5} \right)}^2} + 1}  = 5\sqrt 2  < {R_1} + {R_2} = 10\)

\( \Rightarrow \) Hai đường tròn đã cho cắt nhau \( \Rightarrow \) hai đường tròn có 2 đường tiếp tuyến chung.

Gọi \(\Delta :\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\) là tiếp tuyến chung của hai đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\)

Khi đó ta có: \(\left\{ \begin{array}{l}d\left( {{I_1};\,\,\Delta } \right) = {R_1}\\d\left( {{I_2};\,\,\Delta } \right) = {R_2}\end{array} \right..\)

Lời giải chi tiết:

Đường tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {5;\,\,0} \right)\) và bán kính \({R_1} = 5.\) 

Đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( { - 2;\,\,1} \right)\) và bán kính \({R_2} = \sqrt {{2^2} + 1 + 20}  = 5.\) 

\( \Rightarrow {I_1}{I_2} = \sqrt {{{\left( { - 2 - 5} \right)}^2} + 1}  = 5\sqrt 2  < {R_1} + {R_2} = 10\)

\( \Rightarrow \) Hai đường tròn đã cho cắt nhau \( \Rightarrow \) hai đường tròn có 2 đường tiếp tuyến chung.

Gọi \(\Delta :\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\) là tiếp tuyến chung của hai đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\)

Khi đó ta có: \(\left\{ \begin{array}{l}d\left( {{I_1};\,\,\Delta } \right) = {R_1}\\d\left( {{I_2};\,\,\Delta } \right) = {R_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{\left| {5a + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 5\\\frac{{\left| { - 2a + b + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 5\end{array} \right.\)

\(\begin{array}{l} \Rightarrow \frac{{\left| {5a + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \frac{{\left| { - 2a + b + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\\ \Leftrightarrow \left| {5a + c} \right| = \left| { - 2a + b + c} \right| \Leftrightarrow \left[ \begin{array}{l}5a + c =  - 2a + b + c\\5a + c = 2a - b - c\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}b = 7a\\3a + b + 2c = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}b = 7a\\b =  - 3a - 2c\end{array} \right.\end{array}\)

+) Với \(b = 7a \Rightarrow \frac{{\left| {5a + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 5 \Leftrightarrow \left| {5a + c} \right| = 5\sqrt {{a^2} + 49{a^2}} \)

\(\begin{array}{l} \Leftrightarrow \left| {5a + c} \right| = 25\sqrt 2 \left| a \right| \Leftrightarrow \left[ \begin{array}{l}5a + c = 25\sqrt 2 a\\5a + c =  - 25\sqrt 2 a\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}c = \left( {25\sqrt 2  - 5} \right)a\\c =  - \left( {25\sqrt 2  + 5} \right)a\end{array} \right. \Rightarrow \left[ \begin{array}{l}{\Delta _1}:\,\,\,x + 7y + 25\sqrt 2  - 5 = 0\\{\Delta _2}:\,\,\,x + 7y - 25\sqrt 2  - 5 = 0\end{array} \right.\end{array}\)

+) Với \(b =  - 3a - 2c \Rightarrow \frac{{\left| {5a + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 5\)

\(\begin{array}{l} \Leftrightarrow \left| {5a + c} \right| = 5\sqrt {{a^2} + {{\left( {3a + 2c} \right)}^2}} \\ \Leftrightarrow \left| {5a + c} \right| = 5\sqrt {10{a^2} + 12ac + 4{c^2}} \\ \Leftrightarrow 25{a^2} + 10ac + {c^2} = 25\left( {10{a^2} + 12ac + 4{c^2}} \right)\\ \Leftrightarrow 225{a^2} + 290ac + 99c = 0\end{array}\)

\( \Rightarrow \) Phương trình vô nghiệm.

Vậy có hai tiếp tuyến thỏa mãn bài toán: \(\left[ \begin{array}{l}{\Delta _1}:\,\,\,x + 7y + 25\sqrt 2  - 5 = 0\\{\Delta _2}:\,\,\,x + 7y - 25\sqrt 2  - 5 = 0\end{array} \right.\)

Chọn C.

Phương pháp giải:

Đường tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {0;\,\,2} \right)\) và bán kính \({R_1} = \sqrt {{2^2} + 5}  = 3.\) 

Đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( {3;\,\, - 4} \right)\) và bán kính \({R_2} = \sqrt {{3^2} + {4^2} - 16}  = 3.\) 

\( \Rightarrow {I_1}{I_2} = \sqrt {{3^2} + {{\left( { - 4 - 2} \right)}^2}}  = 3\sqrt 5  > {R_1} + {R_2} = 6\)

\( \Rightarrow \) Hai đường tròn đã cho ngoài \( \Rightarrow \) hai đường tròn có 4 đường tiếp tuyến chung.

Gọi \(\Delta :\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\) là tiếp tuyến chung của hai đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\)

Khi đó ta có: \(\left\{ \begin{array}{l}d\left( {{I_1};\,\,\Delta } \right) = {R_1}\\d\left( {{I_2};\,\,\Delta } \right) = {R_2}\end{array} \right..\)

Lời giải chi tiết:

Đường tròn \(\left( {{C_1}} \right)\) có tâm \({I_1}\left( {0;\,\,2} \right)\) và bán kính \({R_1} = \sqrt {{2^2} + 5}  = 3.\) 

Đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2}\left( {3;\,\, - 4} \right)\) và bán kính \({R_2} = \sqrt {{3^2} + {4^2} - 16}  = 3.\) 

\( \Rightarrow {I_1}{I_2} = \sqrt {{3^2} + {{\left( { - 4 - 2} \right)}^2}}  = 3\sqrt 5  > {R_1} + {R_2} = 6\)

\( \Rightarrow \) Hai đường tròn đã cho ngoài \( \Rightarrow \) hai đường tròn có 4 đường tiếp tuyến chung.

Gọi \(\Delta :\,\,ax + by + c = 0\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)\) là tiếp tuyến chung của hai đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right).\)

Khi đó ta có: \(\left\{ \begin{array}{l}d\left( {{I_1};\,\,\Delta } \right) = {R_1}\\d\left( {{I_2};\,\,\Delta } \right) = {R_2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{\left| {2b + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 3\\\frac{{\left| {3a - 4b + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 3\end{array} \right.\)

\(\begin{array}{l} \Rightarrow \left| {2b + c} \right| = \left| {3a - 4b + c} \right| \Leftrightarrow \left[ \begin{array}{l}2b + c = 3a - 4b + c\\2b + c =  - 3a + 4b - c\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}3a = 6b\\3a - 2b + 2c = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 2b\\b = \frac{{3a + 2c}}{2}\end{array} \right.\end{array}\)

+) Với \(a = 2b \Rightarrow \frac{{\left| {2b + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 3 \Leftrightarrow \left| {2b + c} \right| = 3\sqrt {4{b^2} + {b^2}} \)

\(\begin{array}{l} \Leftrightarrow \left| {2b + c} \right| = 3\sqrt 5 \left| b \right| \Leftrightarrow \left[ \begin{array}{l}2b + c = 3\sqrt 5 b\\2b + c =  - 3\sqrt 5 b\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}c = \left( {3\sqrt 5  - 2} \right)b\\c =  - \left( {3\sqrt 5  + 2} \right)b\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = 2b\\c = \left( {3\sqrt 5  - 2} \right)b\end{array} \right.\\\left\{ \begin{array}{l}a = 2b\\c =  - \left( {3\sqrt 5  + 2} \right)b\end{array} \right.\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}{\Delta _1}:\,\,\,2x + y + 3\sqrt 5  - 2 = 0\\{\Delta _2}:\,\,2x + y - 3\sqrt 5  - 2 = 0\end{array} \right.\end{array}\)

+) Với \(b = \frac{{3a + 2c}}{2} \Rightarrow \frac{{\left| {2b + c} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 3 \Leftrightarrow \left| {3a + 2c + c} \right| = 3\sqrt {{a^2} + {{\left( {\frac{{3a + 2c}}{2}} \right)}^2}} \)

\(\begin{array}{l} \Leftrightarrow \left| {3a + 3c} \right| = 3\sqrt {\frac{{13{a^2} + 12ac + 4{c^2}}}{4}} \\ \Leftrightarrow \left| {a + c} \right| = \sqrt {\frac{{13{a^2} + 12ac + 4{c^2}}}{4}} \\ \Leftrightarrow 4{\left( {a + c} \right)^2} = 13{a^2} + 12ac + 4{c^2}\\ \Leftrightarrow 9{a^2} + 4ac = 0 \Leftrightarrow a\left( {9a + 4c} \right) = 0\end{array}\)

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}a = 0\\9a + 4c = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 0\\a =  - \frac{4}{9}c\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = 0\\b = c\end{array} \right.\\\left\{ \begin{array}{l}a =  - \frac{4}{9}c\\b = \frac{1}{3}c\end{array} \right.\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}{\Delta _3}:\,\,\,y + 1 = 0\\{\Delta _4}:\,\, - \frac{4}{9}x + \frac{1}{3}y + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{\Delta _3}:\,\,\,y + 1 = 0\\{\Delta _4}:\,\,\,4x - 3y - 9 = 0\end{array} \right..\end{array}\)

Chọn D.

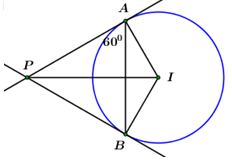
Phương pháp giải:

Đường tròn \(\left( C \right)\) có tâm \(I\left( { - 1;\,\,2} \right)\) và bán kính \(R = \sqrt {1 + {2^2}}  = \sqrt 5 .\)

Ta có: \(M \in d \Rightarrow M\left( {m;\,\,m + 1} \right).\)

Theo đề bài ta có:\(\angle AMB = {60^0} \Rightarrow \Delta AMB\) đều \( \Rightarrow MI = 2IA = 2R = 2\sqrt 5 .\)

Lời giải chi tiết:

Đường tròn \(\left( C \right)\) có tâm \(I\left( { - 1;\,\,2} \right)\) và bán kính \(R = \sqrt {1 + {2^2}}  = \sqrt 5 .\)

 Ta có: \(M \in d \Rightarrow M\left( {m;\,\,m + 1} \right).\)

Theo đề bài ta có:\(\angle AMB = {60^0} \Rightarrow \Delta AMB\) đều \( \Rightarrow MI = 2IA = 2R.\)

\( \Rightarrow M \in \left( {C'} \right)\) với \(\left( {C'} \right)\) là đường tròn tâm \(I\left( { - 1;\,\,2} \right)\) và có bán kính \(R' = 2\sqrt 5 cm.\)

\( \Rightarrow \left( {C'} \right):\,\,\,\,{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 20.\)

\( \Rightarrow \) \(M\) là giao điểm của \(d:\,\,\,x - y + 1 = 0\) và \(\left( {C'} \right).\)

\(\begin{array}{l} \Rightarrow {\left( {m + 1} \right)^2} + {\left( {m + 1 - 2} \right)^2} = 20\\ \Leftrightarrow {m^2} + 2m + 1 + {m^2} - 2m + 1 = 20\\ \Leftrightarrow 2{m^2} = 18\\ \Leftrightarrow {m^2} = 9\\ \Leftrightarrow \left[ \begin{array}{l}m = 3\\m =  - 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}M\left( {3;\,\,4} \right)\\M\left( { - 3; - 2} \right)\end{array} \right..\end{array}\)

Chọn A.

Phương pháp giải:

+) Gọi \(I\left( {a;\,\,b} \right)\) là tâm của đường tròn \(\left( C \right)\)

+) \(IM = R\)

Lời giải chi tiết:

Gọi \(I\left( {a;\,\,b} \right)\) là tâm của đường tròn \(\left( C \right)\).

Trên mặt phẳng tọa độ \(Oxy\), vì \(M\left( {2;\,\,1} \right)\) thuộc góc phần tư thứ (I) và đường tròn tiếp xúc hai trục \(Ox,\,\,Oy\) nên \(I\left( {a;\,\,a} \right)\) với \(a > 0\).

Ta có: \({R^2} = {a^2} = I{M^2} = {\left( {a - 2} \right)^2} + {\left( {a - 1} \right)^2}\)

\( \Rightarrow {a^2} = {\left( {a - 2} \right)^2} + {\left( {a - 1} \right)^2}\)

\( \Leftrightarrow {a^2} = {a^2} - 4a + 4 + {a^2} - 2a + 1\)

\( \Leftrightarrow {a^2} - 6a + 5 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}a = 1\\a = 5\end{array} \right.\)

+) Với \(a = 1\) \( \Rightarrow I\left( {1;\,\,1} \right),\,\,R = 1\).

\( \Rightarrow \) Phương trình đường tròn \(\left( C \right):\,\,{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\)

+) Với \(a = 5 \Rightarrow I\left( {5;\,\,5} \right),\,\,R = 5\)

\( \Rightarrow \) Phưng trình đường tròn \(\left( C \right):\,\,{\left( {x - 5} \right)^2} + {\left( {y - 5} \right)^2} = 25\)

Chọn  A.

Phương pháp giải:

Viết phương trình đường trung trực của đoạn thẳng để xác định tọa tâm của đường tròn \(C\).

Lời giải chi tiết:

Gọi \(I\) là tâm của đường tròn \(\left( C \right)\)

\(\left( {AB} \right):\,\,x - y + 1 = 0 \Rightarrow \overrightarrow {{n_{AB}}}  = \left( {1;\, - 1} \right),\,\,\overrightarrow {{u_{AB}}}  = \left( {1;\,\,1} \right).\)

Gọi \(M\) là trung điểm của đoạn thẳng \(AB\)\( \Rightarrow M\left( {2;\,\,3} \right)\)

Phương trình đường thẳng trung trực của đoạn \(AB\) là \(d:x - 2 + y - 3 = 0 \Leftrightarrow x + y - 5 = 0\)

\( \Rightarrow I\left( {a;\,\,5 - a} \right)\) với \(a \in \mathbb{Z}\)

Ta có: \(R = IA = d\left( {I;\,\,\Delta } \right) = \sqrt {{{\left( {a - 1} \right)}^2} + {{\left( {a - 3} \right)}^2}}  = \frac{{\left| {2a + 2} \right|}}{{\sqrt {10} }}\)

\(\begin{array}{l} \Leftrightarrow 10\left( {{a^2} - 2a + 1 + {a^2} - 6a + 9} \right) = 4{a^2} + 8a + 4\\ \Leftrightarrow 16{a^2} - 88a - 96 = 0\\ \Leftrightarrow \left[ \begin{array}{l}a = 4\,\,\,\left( {tm} \right)\\a = \frac{3}{2}\,\,\,\left( {ktm} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}I\left( {4;\,\,\,1} \right)\\R = \sqrt {10} \end{array} \right..\end{array}\)

Vậy phương trình đường tròn là: \({\left( {x - 4} \right)^2} + {\left( {y - 1} \right)^2} = 10\)\( \Leftrightarrow {x^2} + {y^2} - 8x - 2y + 7 = 0.\)

Chọn  D.

Phương pháp giải:

Chứng minh ba điểm \(ABC\) là tam giác vuông.

Khi đó, độ dài cạnh huyền sẽ là đường kính của đường tròn đi qua ba điểm \(A\left( {0;\,\,4} \right),\,\,B\left( {3;\,\,4} \right),\,\,C\left( {3;\,\,0} \right).\)

Lời giải chi tiết:

Ta có: \(A\left( {0;\,\,4} \right),\,\,B\left( {3;\,\,4} \right),\,\,C\left( {3;\,\,0} \right)\)

\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AB}  = \left( {3;\,\,0} \right)\\\overrightarrow {AC}  = \left( {3;\,\, - 4} \right)\\\overrightarrow {BC}  = \left( {0;\,\, - 4} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}AB = 3\\AC = 5\\BC = 4\end{array} \right.\)

Vì \({5^2} = {4^2} + 3{}^2 \Rightarrow \)\(A{C^2} = A{B^2} + B{C^2}\)

\( \Rightarrow \Delta ABC\) vuông tại \(C\) (định lý Py-ta-go đảo).

\( \Rightarrow \)\(AC\) là đường kính của đường tròn \(\left( C \right)\)\( \Rightarrow R = \frac{{AC}}{2} = \frac{5}{2}\)

Chọn  D.

Phương pháp giải:

+) Phương trình đường tròn tâm \(I\left( {a;\,\,b} \right)\), bán kính \(R\).

Lời giải chi tiết:

\(\left( C \right)\) có \(I\left( { - 2\sqrt 3 ;0} \right)\), \(R = 4\).

Gọi \(J\) là tâm đường tròn cần tìm: \(J(a;b)\)\( \Rightarrow \left( {C'} \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = 4\)

Do \(\left( C \right)\) và \(\left( {C'} \right)\) tiếp xúc ngoài với nhau \( \Rightarrow \sqrt {{{\left( {a + 2\sqrt 3 } \right)}^2} + {b^2}}  = 4 + 2 = 6\)\( \Leftrightarrow {a^2} + 4\sqrt 3 a + {b^2} = 28\)

Vì \(A\left( {0;2} \right)\) là tiếp điểm cho nên : \({\left( {0 - a} \right)^2} + {\left( {2 - b} \right)^2} = 4\left( 2 \right)\)

Do đó ta có hệ: \(\left\{ \begin{array}{l}{\left( {a + 2\sqrt 3 } \right)^2} + {b^2} = 36\\{a^2} + {\left( {2 - b} \right)^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} + 4\sqrt 3 a + {b^2} = 24\\{a^2} - 4b + {b^2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \sqrt 3 \\b = 3\end{array} \right.\)

Giải hệ tìm được: \(b = 3\) và \(a = \sqrt 3  \Rightarrow \left( {C'} \right):{\left( {x - \sqrt 3 } \right)^2} + {\left( {y - 3} \right)^2} = 4\).

Chọn  B.

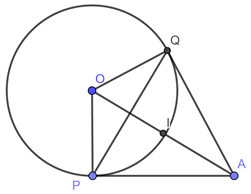
Phương pháp giải:

Chứng minh tứ giác \(OQPA\) là tứ giác nội tiếp đường tròn đường kính \(OA \Rightarrow I\) là trung điểm của \(OA.\)

Lời giải chi tiết:

Đường tròn \(\left( C \right):\,\,\,{x^2} + {y^2} = 4\) có tâm \(O\left( {0;0} \right)\) và bán kính \(R = 2.\)

Ta có: \(A\left( {6;\,\,2} \right) \Rightarrow \overrightarrow {OA}  = \left( {6;\,\,2} \right) \Rightarrow OA = 2\sqrt {10}  > R \Rightarrow \) \(A\left( {6;2} \right)\) nằm ngoài đường tròn.

Lại có: \(I\) là tâm đường tròn ngoại tiếp \(\Delta APQ\) với \(P,\,Q\) là hai tiếp điểm của hai tiếp tuyến kẻ từ \(A\) đến đường tròn \(\left( C \right).\)

Khi đó ta chứng minh được tứ giác \(OPAQ\) là tứ giác nội tiếp.

Lại có: \(\angle OQA = \angle OPA \Rightarrow \) Tâm \(I\) của đường tròn ngoại tiếp tứ giác \(OPAQ\) hay đường tròn ngoại tiếp \(\Delta APQ\) là trung điểm \(OA \Rightarrow \)\(I\left( {3;1} \right)\)

Chọn C.

Phương pháp giải:

+ Xác định tọa độ của hai điểm \(A\) và \(B\)lần lượt là giao điểm của đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) với \(d\).

+ Xác định tọa độ thỏa mãn đề bài: \(MA = 2MB\)

Lời giải chi tiết:

Giả sử đường thẳng \(d\) cắt \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) lần lượt tại hai điểm \(A\) và \(B\).

Ta có:

\(\left( {{C_1}} \right):\,\,{x^2} + {\rm{ }}{y^2}--2x--2y + 1 = 0 \Rightarrow \left\{ \begin{array}{l}{I_1}\left( {1;\,\,1} \right)\\{R_1} = 1\end{array} \right.\)

\(({C_2}):\,\,{x^2} + {\rm{ }}{y^2} + 4x--5 = 0 \Rightarrow \left\{ \begin{array}{l}I\left( { - 2;\,\,0} \right)\\{R_2} = 3\end{array} \right.\)

Gọi \(d\) là đường thẳng qua \(M\) có véc tơ chỉ phương \(\vec u = \left( {a;\,\,b} \right) \Rightarrow d:\,\,\left\{ \begin{array}{l}x = 1 + at\\y = bt\end{array} \right.\).

Đường thẳng \(d\) cắt \(\left( {{C_1}} \right)\) tại \(A\) nên tọa  độ điểm \(A\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}{x^2} + {\rm{ }}{y^2}--2x--2y + 1 = 0\\x = 1 + at\\y = bt\end{array} \right.\)

\( \Rightarrow {\left( {1 + at} \right)^2} + {b^2}{t^2} - 2\left( {1 + at} \right) - 2bt + 1 = 0\)

\( \Leftrightarrow 1 + 2at + {a^2}{t^2} + {b^2}{t^2} - 2 - 2at - 2bt + 1 = 0\)

\( \Leftrightarrow {a^2}{t^2} + {b^2}{t^2} - 2bt = 0\)

\( \Leftrightarrow \left( {{a^2} + {b^2}} \right){t^2} - 2bt = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \frac{{2b}}{{{a^2} + {b^2}}}\end{array} \right.\)

Với \(t = 0 \Rightarrow M\left( {1;\,\,0} \right)\)

Với \(t = \frac{{2b}}{{{a^2} + {b^2}}} \Rightarrow A\left( {1 + \frac{{2ab}}{{{a^2} + {b^2}}};\frac{{2{b^2}}}{{{a^2} + {b^2}}}} \right)\)

Đường thẳng \(d\) cắt \(\left( {{C_2}} \right)\) tại \(B\) nên tọa  độ điểm \(B\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}{x^2} + {\rm{ }}{y^2} + 4x--5 = 0\\x = 1 + at\\y = bt\end{array} \right.\)

\( \Rightarrow {\left( {1 + at} \right)^2} + {b^2}{t^2} + 4.\left( {1 + at} \right) - 5 = 0\)

\( \Leftrightarrow \left( {{a^2} + {b^2}} \right){t^2} + 6at = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}t = 0\\t =  - \frac{{6a}}{{{a^2} + {b^2}}}\end{array} \right.\)

Với \(t = 0 \Rightarrow M\left( {1;\,\,0} \right)\)

Với \(t =  - \frac{{6a}}{{{a^2} + {b^2}}}\)\( \Rightarrow B\left( {1 - \frac{{6{a^2}}}{{{a^2} + {b^2}}};\,\, - \frac{{6ab}}{{{a^2} + {b^2}}}} \right)\)

Theo đề bài, ta có: \(MA = 2MB \Leftrightarrow M{A^2} = 4M{B^2}\)

\( \Rightarrow {\left( {\frac{{2ab}}{{{a^2} + {b^2}}}} \right)^2} + {\left( {\frac{{2{b^2}}}{{{a^2} + {b^2}}}} \right)^2} = 4\left[ {{{\left( {\frac{{6{a^2}}}{{{a^2} + {b^2}}}} \right)}^2} + {{\left( {\frac{{6ab}}{{{a^2} + {b^2}}}} \right)}^2}} \right]\)

\( \Leftrightarrow \frac{{4{b^2}}}{{{a^2} + {b^2}}} = 4.\frac{{36{a^2}}}{{{a^2} + {b^2}}} \Leftrightarrow {b^2} = 36{a^2} \Leftrightarrow \left[ \begin{array}{l}b = 6a\\b =  - 6a\end{array} \right.\)

Với \(b =  - 6a \Rightarrow d:6x + y - 6 = 0\)

Với \(b = 6a \Rightarrow d:6x - y - 6 = 0\)

Chọn  D

Phương pháp giải:

+ Xác định tâm và bán kính của đường tròn \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\).

+ Viết phương trình đường thẳng \(d\) đi qua \(A\) và nhận \(\vec u = \left( {a;\,\,b} \right)\) là VTCP.

+ Xác định tọa độ \(B\) và \(C\) lần lượt là giao điểm của đường thẳng \(\left( d \right)\) với \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\).

+ Đường thẳng \(d\) đi qua \(A\) cắt \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) theo hai dây cung có độ dài bằng nhau thì \(A\) là trung điểm của \(BC\).

Lời giải chi tiết:

Ta có: \(\left( {{C_1}} \right):\,\,{x^2} + {y^2} = 13 \Rightarrow \left\{ \begin{array}{l}I\left( {0;0} \right)\\{R_1} = \sqrt {13} \end{array} \right.\) và \(\left( {{C_2}} \right):\,\;{\left( {x - 6} \right)^2} + {y^2} \Rightarrow \left\{ \begin{array}{l}J\left( {6;\,\,0} \right)\\{R_2} = \sqrt {25} \end{array} \right.\)

Gọi đường thẳng \(d\) qua \(A\left( {2;\,\,3} \right)\) có véc tơ chỉ phương \(\overrightarrow u  = \left( {a;b} \right) \Rightarrow d:\left\{ \begin{array}{l}x = 2 + at\\y = 3 + bt\end{array} \right.\).

Vì \(d\) cắt \(\left( {{C_1}} \right)\) tại \(A\), \(B\) nên tọa điểm \(A\) và  \(B\) là nghiệm của hệ phương trình:\(\left\{ \begin{array}{l}x = 2 + at\\y = 3 + bt\\{x^2} + {y^2} = 13\end{array} \right. \Leftrightarrow \left[ {\left( {{a^2} + {b^2}} \right){t^2} + 2\left( {2a + 3b} \right)t} \right] = 0 \Rightarrow t =  - \frac{{2a + 3b}}{{{a^2} + {b^2}}}\) \( \Rightarrow B\left( {\frac{{b\left( {2b - 3a} \right)}}{{{a^2} + {b^2}}};\,\,\frac{{a\left( {3a - 2b} \right)}}{{{a^2} + {b^2}}}} \right)\).

Tương tự \(d\) cắt \(\left( {{C_2}} \right)\) tại \(A\), \(C\) thì tọa độ của \(A\),\(C\) là nghiệm của hệ phương trình:

\( \Leftrightarrow \left\{ \begin{array}{l}x = 2 + at\\y = 3 + bt\\{\left( {x - 6} \right)^2} + {y^2} = 25\end{array} \right. \Rightarrow t = \frac{{2\left( {4a - 3b} \right)}}{{{a^2} + {b^2}}} \Leftrightarrow C\left( {\frac{{10{a^2} - 6ab + 2{b^2}}}{{{a^2} + {b^2}}};\,\,\frac{{3{a^2} + 8ab - 3{b^2}}}{{{a^2} + {b^2}}}} \right)\)

Nếu 2 dây cung bằng nhau thì \(A\) là trung điểm của \(BC\). Từ đó ta có phương trình :

\(a = 0 \Rightarrow d:\,\,\left\{ \begin{array}{l}x = 2\\y = 3 + t\end{array} \right.\)

\(a = \frac{3}{2}b \Rightarrow \vec u = \left( {\frac{3}{2}b;\,\,b} \right){\rm{ // }}\overrightarrow {u'}  = \left( {3;\,\,2} \right) \Rightarrow d:\left\{ \begin{array}{l}x = 2 + 3t\\y = 3 + 2t\end{array} \right.\)

\( \Leftrightarrow \frac{{\left( {2{b^2} - 3ab} \right)}}{{{a^2} + {b^2}}} + \frac{{10{a^2} - 6ab + 2{b^2}}}{{{a^2} + {b^2}}} = 4 \Leftrightarrow 6{a^2} - 9ab = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\a = \frac{3}{2}\end{array} \right.\)

Vậy có 2 đường thẳng \(d\) là: \(d:x - 2 = 0\) và \(d:2x - 3y + 5 = 0\).

Chọn  A

Phương pháp giải:

+) Xác định tâm và bán kính của đường tròn đã cho

+) Áp dụng công thức tính diện tích tam giác để tìm \(m\).

Lời giải chi tiết:

+) \(\left( C \right):{x^2} + {y^2} - 2x - 2my + {m^2} - 24 = 0 \Rightarrow \left\{ \begin{array}{l}I\left( {1;m} \right)\\R = 5\end{array} \right.\)

+) \(\Delta  \cap \left( C \right) = \left\{ {A;\,B} \right\}\). Gọi \(H\) là trung điểm của \(AB\).

\(IH = d\left( {I,\Delta } \right) = \frac{{\left| {m + 4m} \right|}}{{\sqrt {{m^2} + 16} }} = \frac{{\left| {5m} \right|}}{{\sqrt {{m^2} + 16} }}\)

\(AH = \sqrt {I{A^2} - I{H^2}}  = \sqrt {25 - \frac{{{{\left( {5m} \right)}^2}}}{{{m^2} + 16}}}  = \frac{{20}}{{\sqrt {{m^2} + 16} }}\)

Ta có: \({S_{IAB}} = 12 \Rightarrow \frac{1}{2} \cdot IH \cdot AB = 12\)

\( \Rightarrow IH.\frac{{AB}}{2} = 12 \Leftrightarrow IH.AH = 12\)\( \Leftrightarrow 3{m^2} - 25\left| m \right| + 48 = 0 \Leftrightarrow \left[ \begin{array}{l}m =  \pm 3\\m =  \pm \frac{{16}}{3}\end{array} \right.\)

Vậy có \(4\) giá trị của \(m\) thỏa mãn.

Chọn  A.

Phương pháp giải:

Hai tiếp tuyến tại \(A\), \(B\) của đường tròn tâm \(I\) vuông góc và cắt nhau tại \(M\) khi đó \(IBMA\) là hình vuông.

\(M \in d \Rightarrow \) Tọa độ của điểm \(M\)

Áp dụng các tính chất của hình vuông, định lý Pytago để xác định tọa độ điểm \(M\)

Lời giải chi tiết:

\(\left( C \right):{x^2} + {y^2} - 4x - 2y - 1\,\, = \,\,0 \Rightarrow \left\{ \begin{array}{l}I\left( {2;1} \right)\\R = 2\end{array} \right.\).

\(M\) thuộc \(d\) suy ra \(M(t; - 1 - t)\).

Nếu hai tiếp tuyến vuông góc với nhau thì \(MAIB\) là hình vuông (\(A\),\(B\) là 2 tiếp điểm).

Do đó \(AB = MI = IA\sqrt 2  = R\sqrt 2  = \sqrt 6 .\sqrt 2  = 2\sqrt 3 \)

Ta có : \(MI = \sqrt {{{\left( {2 - t} \right)}^2} + {{\left( {2 + t} \right)}^2}}  = \sqrt {2{t^2} + 8}  = 2\sqrt 3 \)

Do đó : \(2{t^2} + 8 = 12\)\( \Leftrightarrow {t^2} = 2\)\( \Leftrightarrow \left[ \begin{array}{l}t =  - \sqrt 2  \Rightarrow {M_1}\left( { - \sqrt 2 ;\sqrt 2  - 1} \right)\\t = \sqrt 2  \Rightarrow {M_2}\left( {\sqrt 2 ; - \sqrt 2  - 1} \right)\end{array} \right.\)

Chọn  A.

Phương pháp giải:

+) Xác định tâm và bán kính của đường tròn \(\left( {{C_1}} \right),\,\,\left( {{C_2}} \right)\)

+) Xác định phương trình đường thẳng \(d\) cắt \(\left( {{C_1}} \right)\) tại hai điểm \(A,\,\,B\);   đường thẳng \(d\) cắt \(\left( {{C_2}} \right)\) tại hai điểm \(A,\,\,C\);

Lời giải chi tiết:

Theo giả thiết : \(\left( {{C_1}} \right):\;I = \left( {0;0} \right),R = \sqrt {13} .\left( {{C_2}} \right);J\left( {6;0} \right),R' = 5\)

Gọi đường thẳng \(d\) qua \(A\left( {2;3} \right)\) có véc tơ chỉ phương \(\overrightarrow u  = \left( {a;b} \right) \Rightarrow d:\left\{ \begin{array}{l}x = 2 + at\\y = 3 + bt\end{array} \right.\)

\(d\) cắt \(\left( {{C_1}} \right)\) tại \(A\), \(B\): \( \Leftrightarrow \left\{ \begin{array}{l}x = 2 + at\\y = 3 + bt\\{x^2} + {y^2} = 13\end{array} \right. \Leftrightarrow \left[ {\left( {{a^2} + {b^2}} \right){t^2} + 2\left( {2a + 3b} \right)t} \right] = 0 \Rightarrow t =  - \frac{{2a + 3b}}{{{a^2} + {b^2}}}\)

\( \Leftrightarrow B\left( {\frac{{b\left( {2b - 3a} \right)}}{{{a^2} + {b^2}}};\frac{{a\left( {3a - 2b} \right)}}{{{a^2} + {b^2}}}} \right)\).

Tương tự \(d\) cắt \(\left( {{C_2}} \right)\) tại \(A\), \(C\) thì tọa độ của \(A\), \(C\) là nghiệm của hệ : \( \Leftrightarrow \left\{ \begin{array}{l}x = 2 + at\\y = 3 + bt\\{\left( {x - 6} \right)^2} + {y^2} = 25\end{array} \right. \Rightarrow t = \frac{{2\left( {4a - 3b} \right)}}{{{a^2} + {b^2}}}\)\( \Leftrightarrow C\left( {\frac{{10{a^2} - 6ab + 2{b^2}}}{{{a^2} + {b^2}}};\frac{{3{a^2} + 8ab - 3{b^2}}}{{{a^2} + {b^2}}}} \right)\)

Nếu 2 dây cung bằng nhau thì \(A\) là trung điểm của \(A\),\(C\). Từ đó ta có phương trình :

\( \Leftrightarrow \frac{{\left( {2{b^2} - 3ab} \right)}}{{{a^2} + {b^2}}} + \frac{{10{a^2} - 6ab + 2{b^2}}}{{{a^2} + {b^2}}} = 4\)\( \Leftrightarrow 6{a^2} - 9ab = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\a = \frac{3}{2}b\end{array} \right.\)

Với \(a = 0 \Rightarrow \left( d \right):\,\,\left\{ \begin{array}{l}x = 2\\y = 3 + t\end{array} \right. \Rightarrow \left( d \right):x - 2 = 0\).

Với \(a = \frac{3}{2}b \Rightarrow \left( {d'} \right):\left\{ \begin{array}{l}x = 2 + 3t\\y = 3 + 2t\end{array} \right. \Rightarrow \left( {d'} \right):2x - 3y + 5 = 0\)

Vậy ta có hai đường thẳng \(\left( d \right):x - 2 = 0\)  và \(\left( {d'} \right):2x - 3y + 5 = 0\)

Chọn  A.

Phương pháp giải:

Đường tròn \(\left( C \right)\) có tâm \(I\left( {1;\,\,3} \right)\) và bán kính \(R = 2.\)

Ta có: \(\overrightarrow {IM}  = \left( { - 4;\, - 2} \right) \Rightarrow IM = 2\sqrt 5  > R \Rightarrow M\) nằm ngoài đường tròn \(\left( C \right).\)

Gọi \(T\left( {{x_0};\,\,{y_0}} \right)\) là tiếp điểm của tiếp tuyến kẻ từ \(M\) đến \(\left( C \right).\)

Khi đó ta có: \(\left\{ \begin{array}{l}T \in \left( C \right)\\\overrightarrow {MT}  = \overrightarrow {IT} \end{array} \right. \Rightarrow \left\{ \begin{array}{l}T \in \left( C \right)\\\overrightarrow {MT} .\overrightarrow {IT}  = 0\end{array} \right..\)

Lời giải chi tiết:

Đường tròn \(\left( C \right)\) có tâm \(I\left( {1;\,\,3} \right)\) và bán kính \(R = 2.\)

Ta có: \(\overrightarrow {IM}  = \left( { - 4;\, - 2} \right) \Rightarrow IM = 2\sqrt 5  > R \Rightarrow M\) nằm ngoài đường tròn \(\left( C \right).\)

Gọi \(T\left( {{x_0};\,\,{y_0}} \right)\) là tiếp điểm của tiếp tuyến kẻ từ \(M\) đến \(\left( C \right).\)

Khi đó ta có: \(\left\{ \begin{array}{l}T \in \left( C \right)\\\overrightarrow {MT}  = \overrightarrow {IT} \end{array} \right. \Rightarrow \left\{ \begin{array}{l}T \in \left( C \right)\\\overrightarrow {MT} .\overrightarrow {IT}  = 0\end{array} \right..\)

Ta có: \(\overrightarrow {MT}  = \left( {{x_0} + 3;\,\,{y_0} - 1} \right),\,\,\overrightarrow {IT}  = \left( {{x_0} - 1;\,\,{y_0} - 3} \right).\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}x_0^2 + y_0^2 - 2{x_0} - 6{y_0} + 6 = 0\\x_0^2 + y_0^2 + 2{x_0} - 4{y_0} = 0\end{array} \right.\\ \Rightarrow 2{x_0} + {y_0} - 3 = 0\,\,\,\,\left( * \right).\end{array}\)

Như vậy tọa độ các tiếp điểm \({T_1}\) và \({T_2}\) của các tiếp tuyến kẻ từ \(M\) đến \(\left( C \right)\) đều thỏa mãn đẳng thức \(\left( * \right).\)

\( \Rightarrow {T_1}{T_2}:\,\,\,2x + y - 3 = 0.\)

Chọn C.

Phương pháp giải:

Đường tròn \(\left( {{C_1}} \right)\) tiếp xúc với hai trục tọa độ nên \({I_1} \in {d_1}:\,\,\,y = x\) hooặc \({I_1} \in {d_2}:\,\,\,y =  - x.\) \( \Rightarrow {I_1}\left( {a; \pm a} \right)\,\,\,\,\,\left( {a > 0} \right).\)

Đường tròn \(\left( {{C_1}} \right)\) có tâm \({I_1},\) bán kính \({R_1}\) tiếp xúc ngoài với đường tròn \(\left( {{C_2}} \right)\) có tâm \({I_2},\) bán kính \({R_2}\)

\( \Rightarrow {I_1}{I_2} = {R_1} + {R_2}.\)

Lời giải chi tiết:

Đường tròn \(\left( {{C_1}} \right)\) tiếp xúc với hai trục tọa độ nên \({I_1} \in {d_1}:\,\,\,y = x\) hooặc \({I_1} \in {d_2}:\,\,\,y =  - x.\) \( \Rightarrow {I_1}\left( {a; \pm a} \right)\,\,\,\,\,\left( {a > 0} \right).\)

Đường tròn \(\left( C \right)\) có tâm \(I\left( {6;\,\,2} \right)\) và bán kính \(R = \sqrt {{6^2} + {2^2} - 36}  = 2.\)

TH1: Xét \({I_1}\left( {a;\,\,a} \right) \Rightarrow {R_1} = a.\) 

Khi đó ta có:\(\left( C \right),\,\,\left( {{C_1}} \right)\) tiếp xúc ngoài với nhau

\(\begin{array}{l} \Leftrightarrow I{I_1} = {R_1} + {R_2} \Leftrightarrow \sqrt {{{\left( {a - 6} \right)}^2} + {{\left( {a - 2} \right)}^2}}  = 2 + a\\ \Leftrightarrow \sqrt {2{a^2} - 16a + 40}  = a + 2\\ \Leftrightarrow 2{a^2} - 16a + 40 = {a^2} + 4a + 4\\ \Leftrightarrow {a^2} - 20a + 36 = 0\\ \Leftrightarrow \left( {a - 2} \right)\left( {a - 18} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}a - 2 = 0\\a - 18 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 2\,\,\left( {tm} \right)\\a = 18\,\,\left( {tm} \right)\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{I_1}\left( {2;\,\,2} \right)\\{R_1} = 2\end{array} \right.\\\left\{ \begin{array}{l}{I_1}\left( {18;\,\,\,18} \right)\\{R_1} = 18\end{array} \right.\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}\left( {{C_1}} \right):\,\,\,{\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\\\left( {{C_1}} \right):\,\,\,{\left( {x - 18} \right)^2} + {\left( {y - 18} \right)^2} = 324\end{array} \right..\end{array}\)

TH2: Xét \({I_1}\left( {a;\, - a} \right) \Rightarrow {R_1} = a.\) 

Khi đó ta có:\(\left( C \right),\,\,\left( {{C_1}} \right)\) tiếp xúc ngoài với nhau

\(\begin{array}{l} \Leftrightarrow I{I_1} = {R_1} + {R_2} \Leftrightarrow \sqrt {{{\left( {a - 6} \right)}^2} + {{\left( {a + 2} \right)}^2}}  = 2 + a\\ \Leftrightarrow \sqrt {2{a^2} - 8a + 40}  = a + 2\\ \Leftrightarrow 2{a^2} - 8a + 40 = {a^2} + 4a + 4\\ \Leftrightarrow {a^2} - 12a + 36 = 0 \Leftrightarrow {\left( {a - 6} \right)^2} = 0\\ \Leftrightarrow a - 6 = 0 \Leftrightarrow a = 6 \Rightarrow \left\{ \begin{array}{l}{I_1}\left( {2;\,\,2} \right)\\{R_1} = 2\end{array} \right.\\ \Rightarrow \left( {{C_1}} \right):\,\,\,{\left( {x - 6} \right)^2} + {\left( {y - 6} \right)^2} = 36.\end{array}\)

Vậy có 3 đường tròn thỏa mãn bài toán.

Chọn D.

Phương pháp giải:

Viết phương trình AB từ đó tìm được tọa độ điểm A,B. Tìm tọa độ điểm N là giao điểm của AI và BC, từ đó suy ra tọa độ điểm C

Lời giải chi tiết:

Trong mặt phẳng Oxy, cho tam giác ABC cân tại A, nội tiếp trong đường tròn \(\left( C \right):{x^2} + {y^2} + 2x - 4y + 1 = 0\) và \(M\left( {0,1} \right)\). Tìm tọa độ các đỉnh của tam giác ABC biết M là trung điểm cạnh AB và A có hoành độ dương.

Đường tròn \(\left( C \right)\) có tâm \(I\left( { - 1;2} \right)\) bán kính \(R = 2\)

\( \Rightarrow IA = IB\) mà \(MA = MB\) (M là trung điểm cạnh AB)

\( \Rightarrow \) IM là đường trung trực của đoạn AB

Đường thẳng AB đi qua \(M\left( {0;1} \right)\) nhận \(\overrightarrow {IM}  = \left( {1; - 1} \right)\) làm VTPT

\( \Rightarrow \) Phương trình \(\left( {AB} \right):x - y + 1 = 0\)

Tọa độ A,B là nghiệm của hệ:

\(\left\{ \begin{array}{l}x - y + 1 = 0\\{x^2} + {y^2} + 2x - 4y + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1;y = 2\\x =  - 1;y = 0\end{array} \right.\)

\( \Rightarrow A\left( {1;2} \right),B\left( { - 1;0} \right)\) (do \({x_A} > 0\))

Đường thẳng AI đi qua \(A\left( {1;2} \right)\) nhận \(\overrightarrow {IA}  = \left( {2;0} \right)\) làm VTCP

\( \Rightarrow \) Phương trình \(\left( {AI} \right):y - 2 = 0\)

Đường thẳng BC đi qua \(B\left( { - 1;0} \right)\) nhận \(\overrightarrow {IA}  = \left( {2;0} \right)\) làm VTPT (tam giác ABC cân tại A)

\( \Rightarrow \) Phương trình \(\left( {BC} \right):x + 1 = 0\)

Gọi N là giao điểm của AI và BC, tọa độ điểm N là nghiệm của hệ:

\(\left\{ \begin{array}{l}y - 2 = 0\\x + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = 2\end{array} \right. \Rightarrow N\left( { - 1;2} \right)\)

Do tam giác ABC cân tại A nên N là trung điểm của BC \( \Rightarrow C\left( { - 1;4} \right)\)

Chọn B.

Phương pháp giải:

Xác định tâm I và bán kính của đường tròn \(\left( C \right)\), tính AI theo hình vẽ, gọi A theo 1 chữ tìm tọa độ của A

Lời giải chi tiết:

Đường tròn \(\left( C \right)\) có tâm \(I\left( {4; - 3} \right)\) bán kính \(R = \sqrt {16 + 9 - 21}  = 2\)

\( \Rightarrow \left( C \right):\,\,\,{\left( {x - 4} \right)^2} + {\left( {y - 4} \right)^2} = 4.\)

Do hình vuông ABCD ngoại tiếp \(\left( C \right)\)

\(\begin{array}{l} \Rightarrow MN = 2R = 4 = AB = AD\\ \Rightarrow AM = \frac{1}{2}AD = 2\\ \Rightarrow A{I^2} = {2^2} + {2^2} = 8\end{array}\)

 Gọi \(A\left( {a;\,\,1 - a} \right) \in \left( d \right) \Rightarrow {\left( {4 - a} \right)^2} + {\left( {a - 4} \right)^2} = 8\)

\( \Leftrightarrow 2{\left( {a - 4} \right)^2} = 8 \Leftrightarrow \left[ \begin{array}{l}a - 4 = 2\\a - 4 =  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 6 \Rightarrow A\left( {6; - 5} \right)\\a = 2 \Rightarrow A\left( {2; - 1} \right)\end{array} \right.\) 

Chọn D.

Phương pháp giải:

Sử dụng phương trình đường tròn để tìm giá trị lớn nhất của \(Q\) từ đó tìm \(x,y.\)

Lời giải chi tiết:

Ta có \(Q = \sqrt {{{\left( {x + 1} \right)}^2} + {{\left( {y - 3} \right)}^2}}  + \sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} \)

\(\begin{array}{l} \Rightarrow {Q^2} = {\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} + 2\sqrt {{{\left( {x + 1} \right)}^2} + {{\left( {y - 3} \right)}^2}} .\sqrt {{{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} \\ \le 2\left[ {{{\left( {x + 1} \right)}^2} + {{\left( {y - 3} \right)}^2} + {{\left( {x - 1} \right)}^2} + {{\left( {y + 1} \right)}^2}} \right] = 4\left( {{x^2} + {y^2} - 2y + 6} \right) = 4\left[ {{x^2} + {{\left( {y - 1} \right)}^2}} \right] + 20.\end{array}\) 

Vì Q đạt giá trị lớn nhất nên \({Q^2}\) đạt giá trị lớn nhất \( \Leftrightarrow {x^2} + {\left( {y - 1} \right)^2}\) đạt giá trị lớn nhất

Ta có x, y là hai số thực thỏa mãn \({\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 5\)

\( \Rightarrow \) \(\left( {x;y} \right)\) là tọa độ điểm thuộc đường tròn \(\left( C \right)\) tâm \(A\left( {4;3} \right)\) bán kính \(R = \sqrt 5 \)

Mặt khác để \({x^2} + {\left( {y - 1} \right)^2}\) đạt giá trị lớn nhất  \( \Leftrightarrow \left( {x;\,y} \right)\) cũng là điểm thuộc đường tròn \(\left( {C'} \right)\) tâm \(I\left( {0;1} \right)\) sao cho bán kính lớn nhất.

Gọi \(\left( C \right)\) giao tia đối của tia AI tại B

Ta có: \(IA = \sqrt {{4^2} + {2^2}}  = \sqrt {20}  = 2\sqrt 5  > R\)

\( \Rightarrow \) I nằm ngoài đường tròn \(\left( C \right)\)

\( \Rightarrow \) Để thỏa mãn đề bài \( \Leftrightarrow B\left( {x;y} \right)\)

\(\overrightarrow {IA}  = \left( {4;2} \right) \Rightarrow \overrightarrow n  = \left( { - 2;4} \right)\)

Phương trình IA: \( - 2x + 4\left( {y - 1} \right) = 0 \Leftrightarrow  - x + 2y - 2 = 0\)

\(\begin{array}{l}\left\{ \begin{array}{l}B \in \left( {IA} \right)\\B \in \left( C \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l} - x + 2y - 2 = 0\\{\left( {x - 4} \right)^2} + {\left( {y - 3} \right)^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 2\\{\left( {2y - 6} \right)^2} + {\left( {y - 3} \right)^2} = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 2\\5{\left( {y - 3} \right)^2} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 2\\\left[ \begin{array}{l}y - 3 = 1\\y - 3 =  - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y - 2\\\left[ \begin{array}{l}y = 4\\y = 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 6\\y = 4\end{array} \right.\\\left\{ \begin{array}{l}x = 2\\y = 2\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}B\left( {6;4} \right)\\B\left( {2;2} \right)\end{array} \right.\end{array}\)

Vì B và I khác phía với A \( \Rightarrow B\left( {6;4} \right)\)

\( \Rightarrow P = x + y = 6 + 4 = 10\)

Chọn B.

Phương pháp giải:

Sử dụng phương trình đường tròn để tìm giá trị lớn nhất của \(P.\)

Lời giải chi tiết:

Ta có \(x,y\) là hai số thực thỏa mãn \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 4\)

\( \Rightarrow \left( {x;y} \right)\)  là tọa độ điểm thuộc đường tròn \(\left( C \right)\) tâm \(A\left( {1;1} \right)\) bán kính \(R = 2\)

Mặt khác để \(P = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {y - 5} \right)}^2}} \) đạt giá trị lớn nhất \( \Leftrightarrow \left( {x;y} \right)\)  cũng là điểm thuộc đường tròn \(\left( {C'} \right)\) tâm \(I\left( {3;5} \right)\) sao cho bán kính \(R' = P = \sqrt {{{\left( {x - 3} \right)}^2} + {{\left( {y - 5} \right)}^2}} \)  lớn nhất.

Gọi \(\left( C \right)\) giao tia đối của tia AI tại B

Ta có \(IA = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 4} \right)}^2}}  = \sqrt {20}  = 2\sqrt 5  > R\)

\( \Rightarrow \) I nằm ngoài đường tròn \(\left( C \right)\)

\( \Rightarrow \) Để thỏa mãn đề bài \( \Leftrightarrow R' = IB\)

\( \Leftrightarrow P = IA + AB = 2\sqrt 5  + 2 = 2\left( {\sqrt 5  + 1} \right)\)

Chọn D.

Phương pháp giải:

+) \(d\) cắt đường tròn \(\left( C \right)\) theo dây cung có độ dài \(l\) nên khoảng cách từ tâm đường tròn đến \(d\) là\(h = \sqrt {{R^2} - {{\left( {\frac{l}{2}} \right)}^2}} .\)

Lời giải chi tiết:

Giả sử phương trình đường thẳng \(d\) cần tìm và đi qua điểm \(\left( {1;2} \right)\) là \(d:a\left( {x - 1} \right) + b\left( {y - 2} \right) = 0\)\( \Leftrightarrow ax + by - a - 2b = 0\,\,\,\,\left( {{a^2} + {b^2} > 0} \right)\)

Vì \(d\) cắt \(\left( C \right)\) theo dây cung có độ dài  \(l = 8\) nên khoảng cách từ tâm \(I\left( {2; - 1} \right)\) của \(\left( C \right)\) đến \(d\) là:

\(IH = \sqrt {{R^2} - {{\left( {\frac{l}{2}} \right)}^2}}  = \sqrt {25 - {4^2}}  = 3.\)

\( \Rightarrow d\left( {I,d} \right) = \left| {\frac{{2a - b - a - 2b}}{{\sqrt {{a^2} + {b^2}} }}} \right| = 3\)\( \Leftrightarrow \left| {a - 3b} \right| = 3\sqrt {{a^2} + {b^2}} \)

\( \Leftrightarrow 8{a^2} + 6ab = 0 \Leftrightarrow \left[ \begin{array}{l}a = 0\\a =  - \frac{3}{4}b\end{array} \right.\)

+) \(a = 0\); chọn \(b = 1\) suy ra \(d:y - 2 = 0\)

+) \(a = 3;\,\,\,b =  - 4\)\( \Rightarrow d:3x - 4y + 5 = 0\)

Chọn  C.

Phương pháp giải:

Lời giải chi tiết:

\(\left( {{\Delta _\alpha }} \right):\,\,\left( {x - 1} \right)\cos \alpha  + \left( {y - 1} \right)\sin \alpha  - 4 = 0 \Leftrightarrow x\cos \alpha  + y\sin \alpha  - \cos \alpha  - \sin \alpha  - 4 = 0\)

+) Giả sử (C) có tâm \(I\left( {a;b} \right)\) , bán kính R. \(\left( {{\Delta _m}} \right)\) luôn tiếp xúc với đường tròn (C)

\(\begin{array}{l} \Leftrightarrow d\left( {I;{\Delta _\alpha }} \right) = R,\forall \alpha \\ \Leftrightarrow \frac{{\left| {a\cos \alpha  + b\sin \alpha  - \cos \alpha  - \sin \alpha  - 4} \right|}}{{\sqrt {{{\cos }^2}\alpha  + {{\sin }^2}\alpha } }} = R,\forall \alpha \\ \Leftrightarrow \left| {\left( {a - 1} \right)\cos \alpha  + \left( {b - 1} \right)\sin \alpha  - 4} \right| = R,\forall \alpha \\ \Leftrightarrow \left\{ \begin{array}{l}a - 1 = 0\\b - 1 = 0\\R = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 1\\R = 4\end{array} \right.\end{array}\)

Vậy phương trình đường tròn (C) cần tìm là: \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 16\)

Chọn D.

Phương pháp giải:

Lời giải chi tiết:

+) Ta có: \(I\left( { - 2; - 2} \right);R = \sqrt {4 + 4 - 6}  = \sqrt 2 \)

+) Vẽ \(IH \bot AB\)  Khi đó H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây cung).

+) \({S_{ABI}} = \frac{1}{2}IH.AB = IH.HA\)

+) Tam giác vuông IAH vuông tại H ta có: \(I{H^2} + H{A^2} = I{A^2} = 2\)

Theo Cosi ta có: \(\frac{{I{H^2} + H{A^2}}}{2} \ge \sqrt {I{H^2}.H{A^2}}  \Rightarrow IH.HA \le 1 \Rightarrow {S_{ABI\,\,\max }} = 1 \Leftrightarrow IH = HA = 1\) (IH =1 <R thỏa mãn điều kiện)

+) \(d\left( {I,\Delta } \right) = 1 \Leftrightarrow \frac{{\left| { - 2 - 2m - 2m + 3} \right|}}{{\sqrt {1 + {m^2}} }} = 1 \Leftrightarrow \left| { - 4m + 1} \right| = \sqrt {1 + {m^2}} \)

\( \Leftrightarrow 16{m^2} - 8m + 1 = 1 + {m^2} \Leftrightarrow 15{m^2} - 8m = 0 \Leftrightarrow \left[ \begin{array}{l}
m = 0\\
m = \frac{8}{{15}}
\end{array} \right.\)

Vậy \(\left[ \begin{array}{l}m = 0\\m = \frac{8}{{15}}\end{array} \right.\) thỏa mãn yêu cầu bài toán.

Chọn C.

Phương pháp giải:

Sử dụng phương pháp tách tọa độ: \(\left( C \right):\;\;{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}.\)

Tiếp tuyến \(\left( d \right)\) tiếp xúc với \(\left( C \right)\) tại \(T\left( {{x_0};\;{y_0}} \right)\) có phương trình: \(\left( {x - a} \right)\left( {{x_0} - a} \right) + \left( {y - b} \right)\left( {{y_0} - b} \right) = {R^2}.\)

Lời giải chi tiết:

Theo đề bài ta có \(M \in \left( d \right) \Rightarrow M\left( {a;\;2a + 10} \right).\)

Giả sử \(A\left( {{x_A};\;{y_A}} \right).\) Phương trình tiếp tuyến \(MA\) của đường tròn \(\left( C \right)\) là: \(x.{x_A} + y.{y_A} - 4 = 0.\)

Vì \(M \in MA \Rightarrow a{x_A} + \left( {2a + 10} \right){y_A} - 4 = 0\;\;\;\left( 1 \right).\)

Giả sử \(B\left( {{x_B};\;{y_B}} \right).\) Phương trình tiếp tuyến \(MB\) của đường tròn \(\left( C \right)\) là: \(x.{x_B} + y.{y_B} - 4 = 0.\)

Vì \(M \in MB \Rightarrow a{x_B} + \left( {2a + 10} \right){y_B} - 4 = 0\;\;\;\left( 2 \right).\)

Từ (1) và (2) ta có phương trình đường thẳng \(AB\) là: \(ax + \left( {2a + 10} \right)y - 4 = 0.\)

Theo đề bài ta có \(AB\) qua \(N\left( {1;\;0} \right) \Rightarrow a.1 + \left( {2a + 10} \right).0 - 4 = 0 \Leftrightarrow a = 4.\)

\( \Rightarrow M = \left( {a;\;2a + 10} \right) = \left( {4;\;18} \right).\)

Chọn D.