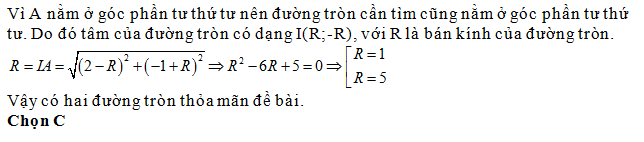Phương pháp giải:

Lời giải chi tiết:

\(\eqalign{
& 2{x^2} + 2{y^2} - 3x + 4y-1 = 0 \cr
& \Rightarrow {x^2} + {y^2} - {3 \over 2}x + 2y-{1 \over 2} = 0 \cr
& \Rightarrow {\left( {x - {3 \over 4}} \right)^2} + {\left( {y + 1} \right)^2} = {1 \over 2} + {9 \over {16}} + 1 = {{33} \over {16}} \cr
& \Rightarrow I\left( {{3 \over 4}; - 1} \right);R = {{\sqrt {33} } \over 4} \cr} \)

Chọn C.

Lời giải chi tiết:

Lời giải chi tiết:

Phương pháp giải:

Biến đổi tương đương\({{x}^{2}}+{{y}^{2}}+2ax+2by+c=0\Leftrightarrow {{\left( x+a \right)}^{2}}+{{\left( y+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-c\)

Lời giải chi tiết:

\({{x}^{2}}+{{y}^{2}}+2ax+2by+c=0,\)là phương trình đường tròn khi \({{R}^{2}}={{a}^{2}}+{{b}^{2}}-c\). Điều này có nghĩa là \({{a}^{2}}+{{b}^{2}}-c>0\)  hay \({{a}^{2}}+{{b}^{2}}>c\).

Chọn D.

Phương pháp giải:

Biến đổi phương trình về dạng \({{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{R}^{2}}\), sử dụng điều kiện \({{R}^{2}}>0\)

Lời giải chi tiết:

\({{x}^{2}}+{{y}^{2}}-2\left( m+2 \right)x+4my+19m-6=0\,\,\,\,\left( * \right)\)

(*) là phương trình đường tròn khi \({{\left( m+2 \right)}^{2}}+{{\left( 2m \right)}^{2}}-19m+6>0\Leftrightarrow 5{{m}^{2}}-15m+10>0\)\(\Leftrightarrow \) \(m<1\) hoặc \(m>2\)

Chọn C.

Phương pháp giải:

+) Phương trình đường tròn có dạng \({{x}^{2}}+{{y}^{2}}+2ax+2by+c=0\) với các hệ số \(a,b,c\) thỏa mãn điều kiện \({{a}^{2}}+{{b}^{2}}>c\)có tâm \(I(-a;-b)\)và bán kính \(R=\sqrt{{{a}^{2}}+{{b}^{2}}-c}\)

+) \((C)\) đi qua điểm \(M({{x}_{0}};{{y}_{0}})\) khi và chỉ khi \({{x}_{0}}^{2}+{{y}_{0}}^{2}+2a{{x}_{0}}+2b{{y}_{0}}+c=0\)

+) \((C)\) không đi qua điểm \(N({{x}_{0}};{{y}_{0}})\) khi và chỉ khi \({{x}_{0}}^{2}+{{y}_{0}}^{2}+2a{{x}_{0}}+2b{{y}_{0}}+c\ne 0\)

Lời giải chi tiết:

\((C):{{x}^{2}}+{{y}^{2}}+2x+4y-20=0\) có \(a=-1,\,\,b=-2,c=-20\) sẽ có tâm \(I\left( -1;-2 \right)\) và bán kính \(R=\sqrt{{{1}^{2}}+{{2}^{2}}+20}=5\). Suy ra mệnh đề sai là mệnh đề ở đáp án A.

Chọn A.

Phương pháp giải:

Phương trình đường tròn (C) có đường kính AB có tâm I là trung điểm của AB và bán kính \(R=\frac{AB}{2}\). Sau đó áp dụng cách viết phương trình đường tròn có tâm tâm \(I(a;b)\) và bán kính \(R\) là:  \({{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{R}^{2}}\)

Lời giải chi tiết:

Gọi I là trung điểm của AB.

Khi đó \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2} = \frac{{6 - 2}}{2} = 2\\{y_I} = \frac{{{y_A} + {y_B}}}{2} = \frac{{2 + 0}}{2} = 1\end{array} \right. \Rightarrow I\left( {2;1} \right)\)

Mặt khác \(R=\frac{AB}{2}=\frac{\sqrt{{{\left( 6+2 \right)}^{2}}+{{\left( 2-0 \right)}^{2}}}}{2}=\frac{2\sqrt{17}}{2}=\sqrt{17}\)

Khi đó, (C) có dạng là:  \({{\left( x-2 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=17\).

Chọn A.

Phương pháp giải:

Tìm điểm \(I({{x}_{I}};{{y}_{I}})\) nằm trên đường thẳng \(x+y+2=0\) và thỏa mãn điều kiện \(IA=IB\). Phương trình đường tròn (C) có tâm  \(I({{x}_{I}};{{y}_{I}})\) và bán kính \(R=IA=IB\).

Lời giải chi tiết:

Giả sử điểm \(I({{x}_{I}};{{y}_{I}})\) là tâm của đường tròn (C). Vì I nằm trên đường thẳng \(x+y+2=0\) nên ta có \({{x}_{I}}+{{y}_{I}}+2=0\)   (1)

Vì đường tròn (C) đi qua hai điểm \(A\left( 0;1 \right),\,\,B\left( 1;0 \right)\) nên ta có \(IA=IB\). Điều này tương đương với

\(I{{A}^{2}}=I{{B}^{2}}\)  hay

\(\begin{array}{l}{\left( {{x_I}} \right)^2} + {\left( {1 - {y_I}} \right)^2} = {\left( {1 - {x_I}} \right)^2} + {\left( {{y_I}} \right)^2}\\ \Leftrightarrow x_I^2 + y_I^2 - 2{y_I} + 1 = x_I^2 - 2{x_I} + 1 + y_I^2\\ \Leftrightarrow {x_I} = {y_I}\,\,\,\,\left( 2 \right)\end{array}\)

Từ (1) và (2) suy ra \({{x}_{I}}={{y}_{I}}=-2\). Suy ra \(I\left( -1;-1 \right)\).

Mặt khác ta có \(R=IA=\sqrt{{{\left( -1 \right)}^{2}}+{{\left( -1-1 \right)}^{2}}}=\sqrt{5}\) 

Vậy (C) có dạng \({{\left( x+1 \right)}^{2}}+{{\left( y+1 \right)}^{2}}=5\)

Chọn D

Phương pháp giải:

Thay trực tiếp tọa độ của 3 điểm vào phương trình trong mỗi đáp án.

 Nếu xuất hiện một mệnh đề sai ở bước nào thì dừng lại và kết luận phương trình đó không qua 3 điểm A,B,C. Nếu có đủ 3 mệnh đề đúng thì kết luận phương trình đó qua 3 điểm A,B,C.

Lời giải chi tiết:

Cách làm:

A. \({{x}^{2}}+{{y}^{2}}=8\). Ta thay \(A(0;2)\) vào phương trình có \({{0}^{2}}+{{2}^{2}}=8\) là mệnh đề sai. Loại A

B. \({{x}^{2}}+{{y}^{2}}+2x+4=0\). Ta thay \(A(0;2)\) vào phương trình có \({{0}^{2}}+{{2}^{2}}+2.0+4=0\) là mệnh đề sai. Loại B

C. \({{x}^{2}}+{{y}^{2}}-2x-8=0\) Ta thay \(A(0;2)\) vào phương trình có \({{0}^{2}}+{{2}^{2}}-2.0-8=0\) là mệnh đề sai. Loại C.

Chọn D.

Phương pháp giải:

\(\left( C \right)\) tiếp xúc \(\text{Ox}\Rightarrow R=d\left( I,\text{Ox} \right)\)

Lời giải chi tiết:

\(\left( C \right)\) tiếp xúc \(\text{Ox}\Rightarrow R=d\left( I,\text{Ox} \right)\). Mặt khác \(I\left( 6;-7 \right)\Rightarrow R=|-7|=7\)

\(\left( C \right)\) tâm \(I(6;-7),\,R=7\Rightarrow \left( C \right):{{\left( x-6 \right)}^{2}}+{{\left( y+7 \right)}^{2}}={{7}^{2}}\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 12x + 36 + {y^2} + 14y + 49 = 49\\ \Leftrightarrow {x^2} + {y^2} - 12x + 14y + 36 = 0\end{array}\)

Chọn B.

Phương pháp giải:

\(\left( C \right)\) tiếp xúc \(\text{Oy}\Rightarrow R=d\left( I,\text{Oy} \right)\)

Lời giải chi tiết:

\(\left( C \right)\) tiếp xúc \(\text{Oy}\Rightarrow R=d\left( I,\text{Oy} \right)\). Mặt khác \(I\left( 5;-2 \right)\Rightarrow R=\left| 5 \right|=5\)

\(\left( C \right)\) tâm \(I(5;-2),\,R=5\Rightarrow \left( C \right):{{\left( x-5 \right)}^{2}}+{{\left( y+2 \right)}^{2}}={{5}^{2}}\)

\(\begin{array}{l} \Leftrightarrow {x^2} - 10x + 25 + {y^2} + 4y + 4 = 25\\ \Leftrightarrow {x^2} + {y^2} - 10x + 4y + 4 = 0\end{array}\)

Chọn A.

Phương pháp giải:

Đường tròn (C)  tiếp xúc với đường thẳng \(\Delta :\)khi ta có  \(d\left( I;\Delta  \right)=R\)

Áp dụng công thức tính khoảng cách từ điểm \(I({{x}_{0}};{{y}_{0}})\) đến  \(\Delta :\,\,ax+by+c=0\)  là: \(d\left( I;\Delta  \right)=\frac{\left| \text{a}{{\text{x}}_{0}}+b{{y}_{0}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\)

Lời giải chi tiết:

\(\left( C \right)\) tiếp xúc \(d\Rightarrow R=d(I,d)=\frac{|-2+2.2+1|}{\sqrt{{{1}^{2}}+{{2}^{2}}}}=\frac{3}{\sqrt{5}}\)

\(\left( C \right)\) tâm \(I\left( -2;2 \right),\,R=\frac{3}{\sqrt{5}}\Rightarrow \left( C \right):{{(x+2)}^{2}}+{{\left( y-2 \right)}^{2}}=\frac{9}{5}\)

\(\begin{array}{l} \Leftrightarrow {x^2} + 4x + 4 + {y^2} - 4y + 4 = \frac{9}{5}\\ \Leftrightarrow {x^2} + {y^2} + 4x - 4y + \frac{{31}}{5} = 0\end{array}\)   

Chọn B.

Phương pháp giải:

Giả sử đường tròn tâm I, bán kính R. Sử dụng tính chất:

Đường tròn tiếp xúc với đường thẳng  d tại A nên ta có: \(\left\{ \begin{array}{l}\overrightarrow {AI} .\overrightarrow {{u_d}}  = 0\\R = AI\end{array} \right.\).

Lời giải chi tiết:

Đường tròn có tâm thuộc đường thẳng \(\Delta :2x+y=0\) , giả sử \(I(i;-2i)\).

Vì đường tròn tiếp xúc với đường thẳng  \(d:x-7y+10=0\) tại \(A(4;2)\) nên ta có: \(\left\{ \begin{array}{l}\overrightarrow {AI} .\overrightarrow {{u_d}}  = 0\\R = AI\end{array} \right.\).

 Mà \(\overrightarrow{AI}=\left( i-4;-2i-2 \right),\overrightarrow{{{u}_{d}}}=\left( 7;1 \right)\)  nên ta có

\(7(i-4)+1.(-2i-2)=0\Leftrightarrow 5i-30=0\Leftrightarrow i=6\Rightarrow I(6;-12)\)

Và  \(\overrightarrow{AI}=\left( 2;-14 \right)\Rightarrow R=AI=\sqrt{{{2}^{2}}+{{\left( -14 \right)}^{2}}}=10\sqrt{2}\).

Vậy ta có phương trình \({{\left( x-6 \right)}^{2}}+{{\left( y+12 \right)}^{2}}=200\)  

Chọn D.

Phương pháp giải:

Giả sử đường tròn có tâm I và bán kính R. Sử dụng tính chất:

Lời giải chi tiết:

Giả sử đường tròn có tâm \(I(a;b)\)

Vì đường tròn tiếp xúc với đường thẳng \((d):2x+y-3=0\)   tại \(B(1;1)\) nên ta có: \(\overrightarrow{BI}.\overrightarrow{{{u}_{d}}}=0\).

 Mà \(\overrightarrow{BI}=\left( a-1;b-1 \right),\overrightarrow{{{u}_{d}}}=(1;-2)\)  nên ta có

\(1\left( a-1 \right)-2\left( b-1 \right)=0\Leftrightarrow a-2b+1=0\,\,\,\,\left( 1 \right)\)

Vì đường tròn qua \(A\left( 3;3 \right)\) nên ta có \(R=IA=IB\)

\(IA=IB\Leftrightarrow {{\left( a-3 \right)}^{2}}+{{\left( b-3 \right)}^{2}}={{\left( a-1 \right)}^{2}}+{{\left( b-1 \right)}^{2}}\Leftrightarrow -4a-4b+16=0\Leftrightarrow a+b=4\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta có hệ \(\left\{ \begin{array}{l}a - 2b + 1 = 0\\a + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{7}{3}\\b = \frac{5}{3}\end{array} \right. \Rightarrow I\left( {\frac{7}{3};\frac{5}{3}} \right)\)

Ta có \(R=BI=\sqrt{{{\left( \frac{7}{3}-1 \right)}^{2}}+{{\left( \frac{5}{3}-1 \right)}^{2}}}=\sqrt{\frac{20}{9}}\)

Vậy ta có phương trình \({{\left( x-\frac{7}{3} \right)}^{2}}+{{\left( y-\frac{5}{3} \right)}^{2}}=\frac{20}{9}\)

Chọn A.

Phương pháp giải:

Đường tròn (C)  tiếp xúc với đường thẳng \(\Delta :\) khi ta có  \(d(I;\Delta )=R\)

Áp dụng công thức tính khoảng cách từ điểm \(I({{x}_{0}};{{y}_{0}})\) đến \(\Delta :\,\,ax+by+c=0\)  là \(d\left( I;\Delta  \right)=\frac{\left| \text{a}{{\text{x}}_{0}}+b{{y}_{0}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\)

Lời giải chi tiết:

Giả sử \(I(a;b)\) là tâm của đường tròn (C) với \(a>0\)  

Theo giả thiết \(I(a;b)\) nằm trên đường thẳng \(d:\)\(x+y+1=0\) nên ta có \(I(a;-1-a)\).

Vì đường tròn (C) có bán kính bằng 5, tiếp xúc với đường thẳng \(\Delta :\)\(3x+4y-20=0\)  nên ta có

\(d(I;\Delta )=R\)  \(\frac{{\left| {3.a + 4\left( { - 1 - a} \right) - 20} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 5 \Leftrightarrow \left| { - a - 24} \right| = 25 \Leftrightarrow \left[ \begin{array}{l} - a - 24 = 25\\ - a - 24 =  - 25\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a =  - 49\\a = 1\end{array} \right.\)

Vì  \(a>0\)  nên chọn a = 1.

\((C)\) có tâm \(I\left( 1;-2 \right)\) và \(R=5\)\(\Rightarrow (C):{{\left( x-1 \right)}^{2}}+{{\left( y+2 \right)}^{2}}=25\)

Chọn C.

Phương pháp giải:

Đường tròn đường kính AB có tâm I là trung điểm của AB, bán kính \(R = \frac{{AB}}{2}\).

Lời giải chi tiết:

Tọa độ trung điểm I của AB:  \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = \frac{{1 + 3}}{2}\\{y_I} = \frac{{1 + 5}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_I} = 2\\{y_I} = 3\end{array} \right. \Rightarrow I(2;3)\)

\(R = \frac{{AB}}{2} = \frac{{\sqrt {{{(3 - 1)}^2} + {{(5 - 1)}^2}} }}{2} = \sqrt 5 \)

Phương trình đường tròn đường kính AB: \({(x - 2)^2} + {(y - 3)^2} = 5 \Leftrightarrow {x^2} + {y^2} - 4x - 6y + 8 = 0\)

Chọn: A

Phương pháp giải:

Giải hệ phương trình tọa độ giao điểm: \(\left\{ \begin{array}{l}{x^2} + {y^2} - 2 = 0\\{x^2} + {y^2} - 2x = 0\end{array} \right.\)

Lời giải chi tiết:

Tọa độ giao điểm của hai đường tròn \(\left( {{C_1}} \right):\,\,{x^2} + {y^2} - 2 = 0\) và \(\left( {{C_2}} \right):{x^2} + {y^2} - 2x = 0\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}{x^2} + {y^2} - 2 = 0\\{x^2} + {y^2} - 2x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} - 2 = 0\\2 - 2x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{1^2} + {y^2} - 2 = 0\\x = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}y = 1\\y =  - 1\end{array} \right.\\x = 1\end{array} \right.\)

Vậy, tọa độ 2 giao điểm là \(\left( {1; - 1} \right)\) và \(\left( {1;1} \right)\).

Chọn: C

Phương pháp giải:

Lời giải chi tiết:

+) Ta có: \(R = d\left( {I;\Delta } \right) = \frac{{\left| {2.2 + 1 + 4} \right|}}{{\sqrt {{2^2} + {1^2}} }} = \frac{9}{{\sqrt 5 }}\)

+) Phương trình đường tròn (C) là: \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{81}}{5}\) .

Chọn D.

Phương pháp giải:

Đường tròn \({x^2} + {y^2} - 2ax - 2by + c = 0\) có tâm \(I\left( {a;b} \right)\), bán kính \(R = \sqrt {{a^2} + {b^2} - c} \)

Lời giải chi tiết:

Đường tròn \(\left( C \right):{x^2} + {y^2} + 4x + 6y - 12 = 0\) có tâm \(I\left( { - 2; - 3} \right)\)

Chọn A.

Phương pháp giải:

Đường thẳng \(\Delta \) là tiếp xúc với đường tròn \(\left( {O,R} \right) \Leftrightarrow d\left( {O,\Delta } \right) = R\)

Lời giải chi tiết:

Đường tròn có tâm \(I\left( {3;4} \right)\) tiếp xúc với đường thẳng \(\Delta :3x + 4y - 10 = 0\)

\( \Leftrightarrow R = d\left( {I,\Delta } \right) = \frac{{\left| {3.3 + 4.4 - 10} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{15}}{5} = 3\)

Chọn C.

Phương pháp giải:

Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( {O,R} \right)\) tại \(A \in \left( {O,R} \right)\)\( \Leftrightarrow OA \bot \Delta \) tại A

Lời giải chi tiết:

Đường tròn \(\left( C \right)\) có tâm \(O\left( {1;2} \right)\) và bán kính \(R = 3.\)

Gọi \(\Delta \) là tiếp tuyến của \(\left( C \right)\) tại A

Ta có: \(\overrightarrow {OA}  = \left( {0;3} \right)\) là một VTCP của \(\Delta \)

 Phương trình \(\Delta \): \(0.\left( {x - 1} \right) + 3\left( {y - 5} \right) = 0 \Leftrightarrow y - 5 = 0\)

Chọn A.

Phương pháp giải:

Đường tròn \(\left( C \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = c\) có tâm \(I\left( {a;b} \right)\), bán kính \(R = \sqrt c \)

Lời giải chi tiết:

Phương trình đường tròn \((C)\) có tâm \(I\left( {2; - 3} \right)\) và có bán kính \(R = 4\) là \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 16\)

Chọn D.

Phương pháp giải:

Đường tròn \(\left( C \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = c\) có tâm \(I\left( {a;b} \right)\), bán kính \(R = \sqrt c \)

Lời giải chi tiết:

Đường tròn \((C):{\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\) có tâm \(I\left( { - 1;2} \right)\), bán kính \(R = 2\)

Dễ thấy \(d\left( {I,Oy} \right) = 1 < 2 = R\) nên đường tròn \(\left( C \right)\) cắt trục \(Oy\) tại hai điểm phân biệt.

Chọn D.

Phương pháp giải:

Đường thẳng \(\Delta \) là tiếp tuyến của đường tròn \(\left( {O;R} \right) \Leftrightarrow d\left( {O,\Delta } \right) = R\)

Lời giải chi tiết:

Đường tròn tâm \(I\left( {1;3} \right)\) tiếp xúc với đường thẳng \(\Delta :3x + 4y = 0\)

\( \Leftrightarrow R = d\left( {I,\Delta } \right) = \frac{{\left| {3.1 + 4.3} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{15}}{5} = 3\)

Chọn A.

Phương pháp giải:

Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( C \right)\) tâm I  bán kính R \( \Leftrightarrow d\left( {I;\Delta } \right) = R.\)

Cho đường thẳng \(\Delta :ax + by + c = 0\) và điểm \({M_0}\left( {{x_0};{y_0}} \right) \Rightarrow d\left( {{M_0};\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}.\)  

Lời giải chi tiết:

Đường tròn \(\left( C \right)\) có tâm \(I\left( {0;0} \right)\) bán kính \(R = \sqrt {0 + 0 + 16}  = 4\)

Đường thẳng \(\Delta \) tiếp xúc với đường tròn \(\left( C \right)\)\( \Leftrightarrow d\left( {I;\Delta } \right) = R\)

\( \Leftrightarrow \frac{{\left| {m - 1} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 4 \Leftrightarrow \left| {m - 1} \right| = 20 \Leftrightarrow \left[ \begin{array}{l}m - 1 = 20\\m - 1 =  - 20\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 21\\m =  - 19\end{array} \right.\)

Chọn D.

Phương pháp giải:

Phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình đường tròn \( \Leftrightarrow {a^2} + {b^2} - c > 0\).

Lời giải chi tiết:

\({x^2} + {y^2} + 2mx - 4\left( {m + 1} \right)y + 4{m^2} + 5m + 2 = 0\,\,\,\left( 1 \right)\)

Có \(a =  - m,\,\,b = 2\left( {m + 1} \right),\) \(c = 4{m^2} + 5m + 2\)

(1) là phương trình đường tròn \( \Leftrightarrow {a^2} + {b^2} - c > 0\)

\(\begin{array}{l} \Leftrightarrow {\left( { - m} \right)^2} + 4{\left( {m + 1} \right)^2} - \left( {4{m^2} + 5m + 2} \right) > 0\\ \Leftrightarrow {m^2} + 4\left( {{m^2} + 2m + 1} \right) - 4{m^2} - 5m - 2 > 0\\ \Leftrightarrow {m^2} + 4{m^2} + 8m + 4 - 4{m^2} - 5m - 2 > 0\\ \Leftrightarrow {m^2} + 3m + 2 > 0\\ \Leftrightarrow \left( {m + 1} \right)\left( {m + 2} \right) > 0\\ \Leftrightarrow \left[ \begin{array}{l}m >  - 1\\m <  - 2\end{array} \right.\end{array}\)

Chọn C.

Phương pháp giải:

Cách 1: Xác định tọa độ giao điểm của đường tròn \(\left( C \right)\) và đường thẳng \(\left( \Delta  \right)\)

Cách 2: So sánh khoảng cách từ tâm đường tròn \(\left( C \right)\) đến đường thẳng \(\left( \Delta  \right)\) với \(R\)

Lời giải chi tiết:

Đường tròn \(\left( C \right):\,\,{x^2} + {y^2} - 4x - 2y = 0\) có tọa độ tâm \(I\left( {2;\,\,1} \right)\) và \(R = \sqrt 5 \)

Thay \(I\left( {2;\,\,1} \right)\) vào \(\Delta :\,\,x + 2y + 1 = 0\) ta được: \(2 + 2.1 + 1 = 5 \ne 0\)

\( \Rightarrow I\left( {2;\,\,1} \right) \notin \left( \Delta  \right)\)

\( \Rightarrow \Delta \) không đi qua tâm của \(\left( C \right)\)

Tọa độ giao điểm của \(\Delta \) và \(\left( C \right)\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}{x^2} + {y^2} - 4x - 2y = 0\\x + 2y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} - 4x - 2y = 0\\x =  - 2y - 1\end{array} \right.\)

\( \Rightarrow {\left( { - 2y - 1} \right)^2} + {y^2} - 4.\left( { - 2y - 1} \right) - 2y = 0\)

\( \Leftrightarrow 4{y^2} + 4y + 1 + {y^2} + 8y + 4 - 2y = 0\)

\( \Leftrightarrow 5{y^2} + 10y + 5 = 0\)

\( \Leftrightarrow y =  - 1\)

Với \(y =  - 1 \Rightarrow x = 1\)

Vậy tọa độ giao điểm của \(\Delta \) và \(\left( C \right)\) là \(\left( {1;\,\, - 1} \right)\).

Vậy \(\Delta \) tiếp xúc với \(\left( C \right)\).

Chọn  C

Phương pháp giải:

+) Viết phương trình đường thẳng \(\left( \Delta  \right)\) đi qua hai điểm đã cho.

+)  So sánh khoảng cách từ tâm của đường tròn \(\left( C \right)\) đến đường thẳng \(\left( \Delta  \right)\) với bán kính.

(Để đường tròn \(\left( C \right)\) không cắt đường thẳng \(\left( \Delta  \right)\) thì khoảng cách từ tâm của đường tròn \(\left( C \right)\) đến đường thẳn \(\left( \Delta  \right)\) lớn hơn bán kính)

Lời giải chi tiết:

\(\left( C \right):\,\,{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 25 \Rightarrow \left\{ \begin{array}{l}I\left( {2;\,\,1} \right)\\R = 5\end{array} \right.\)

Phương trình đường thẳng  đi qua hai điểm \(\left( {2;\,\,6} \right)\) và \(\left( {45;\,\,50} \right)\) là:

\(\frac{{x - 2}}{{43}} = \frac{{y - 6}}{{44}} \Leftrightarrow 44\,.\left( {x - 2} \right) = 43.\left( {y - 6} \right) \Leftrightarrow 44x - 88 = 43y - 258 \Leftrightarrow 44x - 43y + 170 = 0\)

Phương trình đường thẳng  đi qua hai điểm \(\left( {3;\, - 2} \right)\) và \(\left( {19;\,\,33} \right)\)  là :

\(\frac{{x - 3}}{{16}} = \frac{{y + 2}}{{35}} \Leftrightarrow 35\left( {x - 3} \right) = 16\left( {y + 2} \right) \Leftrightarrow 35x - 105 = 16y + 32 \Leftrightarrow 35x - 16y - 137 = 0\)

Khoảng cách từ tâm đến các đường thẳng là:

\({d_A} = \frac{{215}}{{\sqrt {3785} }} < R;\,\,\,{d_B} = 3 < R;\,\,\,{d_C} = \frac{{19}}{{\sqrt {1481} }} < R;\,\,{d_D} = 6 > R\)

Chọn  D

Phương pháp giải:

Đường tròn đường kính AB có tâm là trung điểm AB và bán kính \(R = \frac{{AB}}{2}\).

Công thức viết phương trình đường tròn biết tâm \(I\left( {a;b} \right)\) bán kính \(R\) là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\)

Lời giải chi tiết:

Gọi I là trung điểm của AB. Khi đó \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_I} = \frac{{1 + \left( { - 3} \right)}}{2} =  - 1\\{y_I} = \frac{{3 + 5}}{2} = 4\end{array} \right.\)  \( \Rightarrow I\left( { - 1;4} \right)\)

Ta có: \(AB = \sqrt {{{\left( { - 3 - 1} \right)}^2} + {{\left( {5 - 3} \right)}^2}} \) \( = 2\sqrt 5 \)

Đường tròn đường kính AB có tâm \(I\left( { - 1;4} \right)\) bán kính \(R = \frac{{AB}}{2} = \frac{{2\sqrt 5 }}{2} = \sqrt 5 \) nên có phương trình:

\({\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = {\left( {\sqrt 5 } \right)^2}\)\( \Leftrightarrow {\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = 5\)

Chọn D.

Phương pháp giải:

Phương trình đường tròn tâm \(I\left( {a;\,\,b} \right)\) và bán kính \(R\) là \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}.\)

Lời giải chi tiết:

Phương trình đường tròn tâm \(I\left( {1; - 5} \right)\) và bán kính \(R = 2\sqrt 3 \) là \({\left( {x - 1} \right)^2} + {\left( {y + 5} \right)^2} = 12\)

Chọn A.