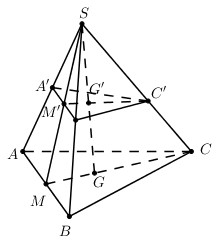
40 bài tập hai đường thẳng chéo nhau và hai đường thẳng song song mức độ vận dụng, vận dụng caoLàm bàiCâu hỏi 1 : Cho tứ diện ABCD có tất cả các cạnh đều bằng a. Gọi \({{G}_{1}},{{G}_{2}}\) lần lượt là trọng tâm tam giác BCD và ACD. Khi đó đoạn thẳng \({{G}_{1}}{{G}_{2}}\) bằng:
Đáp án: B Phương pháp giải: - Sử dụng định lí Ta-let đảo. Lời giải chi tiết: Ta có: \(\frac{E{{G}_{1}}}{EB}=\frac{E{{G}_{2}}}{EA}=\frac{1}{3}\Rightarrow {{G}_{1}}{{G}_{2}}\parallel AB\) (Định lí Ta-let đảo) Khi đó ta có: \(\frac{E{{G}_{1}}}{EB}=\frac{1}{3}=\frac{{{G}_{1}}{{G}_{2}}}{AB}\Rightarrow {{G}_{1}}{{G}_{2}}=\frac{1}{3}AB=\frac{a}{3}.\) Chọn B. Câu hỏi 2 : Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Hình chiếu của A lên mặt phẳng (A’B’C’) là trung điểm H của A’B’. Gọi M là trung điểm của B’C’. Tính cosin của góc giữa hai đường thẳng A’M, AB’ biết \(AH=\frac{a}{2}.\)
Đáp án: C Phương pháp giải: Sử dụng các phương pháp xác định góc – khoảng cách trong không gian Lời giải chi tiết:
Gọi H là trung điểm của \(A'B'\)\(\Rightarrow \,\,AH=\frac{a}{2}.\) Gọi N là trung điểm của BC \(\Rightarrow AN//A'M\) Khi đó \(\widehat{\left( A'M;AB' \right)}=\widehat{\left( AN;AB' \right)}\). Trong tam giác vuông HAB’ ta có \(AB'=\sqrt{A{{H}^{2}}+H{{B}^{2}}}=\frac{a\sqrt{2}}{2}\). Gọi K là trung điểm của AB. Khi đó \(B'K\parallel AH\Rightarrow B'K\bot KN\) \(\Rightarrow B'N=\sqrt{B'{{K}^{2}}+K{{N}^{2}}}=\sqrt{{{\left( \frac{a}{2} \right)}^{2}}+{{\left( \frac{a}{2} \right)}^{2}}}=\frac{a\sqrt{2}}{2}\). Tam giác ABC đều cạnh a nên \(AN=\frac{a\sqrt{3}}{2}\) Áp dụng hệ quả của định lý hàm số cosin trong \(\Delta \,AB'N\) ta có \(\cos \widehat{\left( A'M;AB' \right)}=\left| \cos \widehat{NAB'} \right|=\frac{\left| \frac{2{{a}^{2}}}{4}+\frac{3{{a}^{2}}}{4}-\frac{2{{a}^{2}}}{4} \right|}{2.\frac{a\sqrt{2}}{2}.\frac{a\sqrt{3}}{2}}=\frac{\sqrt{6}}{4}.\) . Chọn C. Câu hỏi 3 : Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(AB=2a,BC=a\). Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB, góc giữa đường thẳng SC và mặt phẳng đáy bằng 600. Tính cosin góc giữa hai đường thẳng SB và AC.
Đáp án: A Phương pháp giải: Sử dụng công thức \(\overrightarrow{SB}.\overrightarrow{AC}=SB.AC.\cos \left( SB;AC \right).\) Lời giải chi tiết:
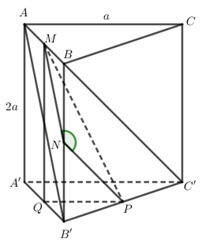
\(HC=\sqrt{B{{H}^{2}}+B{{C}^{2}}}=\sqrt{{{a}^{2}}+{{a}^{2}}}=a\sqrt{2}\) Ta có \(\left( SC;\left( ABCD \right) \right)=\left( SC;HC \right)=\widehat{SCH}={{60}^{0}}\) Xét tam giác vuông SHC có \(SH=HC.\tan 60=a\sqrt{2}.\sqrt{3}=a\sqrt{6}\) Ta có: \(\begin{align} AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{4{{a}^{2}}+{{a}^{2}}}=a\sqrt{5} \\ SB=\sqrt{S{{H}^{2}}+H{{B}^{2}}}=\sqrt{6{{a}^{2}}+{{a}^{2}}}=a\sqrt{7} \\ \end{align}\) Ta có: \(\begin{align} \overrightarrow{SB}.\overrightarrow{AC}=\left( \overrightarrow{SH}+\overrightarrow{HB} \right).\overrightarrow{AC}=\underbrace{\overrightarrow{SH}.\overrightarrow{AC}}_{\overrightarrow{0}}+\overrightarrow{HB}.\overrightarrow{AC}=\overrightarrow{HB}.\overrightarrow{AC} \\ \Rightarrow \overrightarrow{SB}.\overrightarrow{AC}=HB.AC.\cos \left( HB;AC \right)=HB.AC.\cos \widehat{BAC}=HB.AC.\frac{AB}{AC}=a.2a=2{{a}^{2}} \\ \end{align}\) Lại có \(\overrightarrow{SB}.\overrightarrow{AC}=SB.AC.\cos \left( SB;AC \right)\Rightarrow \cos \left( SB;AC \right)=\frac{\overrightarrow{SB}.\overrightarrow{AC}}{SB.AC}=\frac{2{{a}^{2}}}{a\sqrt{7}.a\sqrt{5}}=\frac{2}{\sqrt{35}}\) Chọn A. Câu hỏi 4 : Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, \(AB=BC=a,\,\,AD=2a\), SA vuông góc với mặt đáy (ABCD), SA = a. Gọi M, N lần lượt là trung điểm của SB, CD. Tính cosin của góc giữa MN và AC.
Đáp án: D Phương pháp giải: Từ N kẻ NE // AC \(\Rightarrow \widehat{\left( MN;AC \right)}=\widehat{\left( MN;EN \right)}\) Lời giải chi tiết: Gọi E là trung điểm của AD ta có EN // AC \(\Rightarrow \widehat{\left( MN;AC \right)}=\widehat{\left( MN;EN \right)}\) Gọi G là trung điểm của AB \(\Rightarrow MG//SA\Rightarrow MG\bot \left( ABCD \right)\Rightarrow MG\bot GN\) \(\begin{array}{l}\left\{ \begin{array}{l}MG = \frac{1}{2}SA = \frac{a}{2}\\GN = \frac{{AD + BC}}{2} = \frac{{3a}}{2}\end{array} \right. \Rightarrow MN = \frac{{a\sqrt {10} }}{2}\\EN = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\\GE = \sqrt {\frac{{{a^2}}}{4} + {a^2}} = \frac{{a\sqrt 5 }}{2} \Rightarrow ME = \sqrt {\frac{{{a^2}}}{4} + \frac{{5{a^2}}}{4}} = \frac{{a\sqrt 6 }}{2}\end{array}\) Áp dụng định lí Cosin trong tam giác MNE có : \(\begin{align} \cos \widehat{MNE}=\frac{M{{N}^{2}}+N{{E}^{2}}-M{{E}^{2}}}{2MN.NE}=\frac{3\sqrt{5}}{10}>0 \\ \Rightarrow \cos \widehat{\left( MN;AC \right)}=\cos \widehat{\left( MN;EN \right)}=\frac{3\sqrt{5}}{10} \\ \end{align}\) Chọn D. Câu hỏi 5 : Cho hình lăng trụ \(ABC.A'B'C'\) có đáy ABC là tam giác vuông tại A, \(AB=a,\,AC=a\sqrt{3}\). Hình chiếu vuông góc của A’ lên mặt phẳng (ABC) là trung điểm H của BC, \(A'H=a\sqrt{3}\). Gọi \(\varphi \) là góc giữa hai đường thẳng A’B và B’C. Tính \(\cos \varphi \).
Đáp án: B Phương pháp giải: Sử dụng công thức Côsin: \({{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A\) Lời giải chi tiết: Dựng hình bình hành ABCD (tâm I). Khi đó, A’B’CD là hình bình hành (do \(\overrightarrow{A'B'}=\overrightarrow{AB}=\overrightarrow{DC}\)) \(\Rightarrow A'D//B'C\Rightarrow \left( \widehat{A'B;B'C} \right)=\left( \widehat{A'B;A'D} \right)\) Tam giác ABC vuông tại A \(\begin{align} \Rightarrow BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=\sqrt{{{a}^{2}}+{{\left( a\sqrt{3} \right)}^{2}}} \\ =2a \\ \end{align}\) H là trung điểm của BC \(\Rightarrow HB=HC=a\) Tam giác A’BH vuông tại H \(\Rightarrow A'B=\sqrt{A'{{H}^{2}}+H{{B}^{2}}}=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}+{{a}^{2}}}=2a\) Tam giác ABC vuông tại A \(\Rightarrow \cos \widehat{ABC}=\frac{AB}{BC}=\frac{a}{2a}=\frac{1}{2}\) ABCD là hình bình hành \(\Rightarrow AB//CD\Rightarrow \widehat{DCB}={{180}^{0}}-\widehat{ABC}\Rightarrow \cos \widehat{DCB}=-\cos \widehat{ABC}=-\frac{1}{2}\) Tam giác BCD: \(BD=\sqrt{B{{C}^{2}}+C{{D}^{2}}-2BC.CD.\cos \widehat{DCB}}=\sqrt{{{\left( 2a \right)}^{2}}+{{a}^{2}}-2.2a.a.\frac{-1}{2}}=a\sqrt{7}\) Tam giác CDH: \(HD=\sqrt{C{{H}^{2}}+C{{D}^{2}}-2CH.CD.\cos \widehat{DCB}}=\sqrt{{{a}^{2}}+{{a}^{2}}-2a.a.\frac{-1}{2}}=a\sqrt{3}\) Tam giác A’DH vuông tại H: \(A'D=\sqrt{A'{{H}^{2}}+H{{D}^{2}}}=\sqrt{{{\left( a\sqrt{3} \right)}^{2}}+{{\left( a\sqrt{3} \right)}^{2}}}=a\sqrt{6}\) Tam giác A’BH: \(\cos \widehat{BA'D}=\frac{A'{{D}^{2}}+A'{{B}^{2}}-B{{D}^{2}}}{2A'D.A'B}=\frac{{{\left( a\sqrt{6} \right)}^{2}}+{{(2a)}^{2}}-{{\left( \sqrt{7}a \right)}^{2}}}{2.a\sqrt{6}.2a}=\frac{3}{4\sqrt{6}}=\frac{\sqrt{6}}{8}\) . Chọn: B Câu hỏi 6 : Cho hình chóp tứ giác đều S.ABCD đáy ABCD là hình vuông, E là điểm đối xứng của D qua trung điểm của SA. Gọi M, N lần lượt là trung điểm của AE và BC. Góc giữa hai đường thẳng MN và BD bằng:
Đáp án: A Phương pháp giải: Gọi P là trung điểm của CD \(\Rightarrow NP//BD\Rightarrow \widehat{\left( MN;BD \right)}=\widehat{\left( MN;NP \right)}\). Gọi H là hình chiếu của M trên (ABCD), chứng minh \(NP\bot \left( MNH \right)\). Lời giải chi tiết: Gọi P là trung điểm của CD \(\Rightarrow NP//BD\Rightarrow \widehat{\left( MN;BD \right)}=\widehat{\left( MN;NP \right)}\). Gọi I là trung điểm của SA, K là trung điểm của AO \(\Rightarrow IK//SO\Rightarrow IK\bot \left( ABCD \right)\). Gọi H là hình chiếu của M trên (ABCD) \(\Rightarrow HK//MI\Rightarrow MIKH\) là hình bình hành \(\Rightarrow HK=MI\). Mặt khác MI là đường trung bình của tam giác EAD \(\Rightarrow MI//AD//BC\) và \(MK=\frac{1}{2}AD=\frac{1}{2}BC=NC\) \(\Rightarrow HKCN\) là hình bình hành \(\Rightarrow HN//AC\). Mà \(AC\bot BD\Rightarrow AC\bot NP\Rightarrow HN\bot NP\). Ta có \(\left\{ \begin{align} NP\bot HN \\ NP\bot MH \\ \end{align} \right.\Rightarrow NP\bot \left( MNH \right)\Rightarrow NP\bot MN\Rightarrow \widehat{\left( MN;NP \right)}={{90}^{0}}\). Chọn A. Câu hỏi 7 : Cho hình lăng trụ tam giác đều \(ABC.{A}'{B}'{C}'\) có \(AB=a\) và \(A{A}'=\sqrt{2}a.\) Góc giữa hai đường thẳng \(A{B}'\) và \(B{C}'\) bằng
Đáp án: D Phương pháp giải: Sử dụng tích vô hướng để tìm góc giữa hai đường thẳng trong không gian Lời giải chi tiết: Ta có \(\left\{ \begin{align} & \overrightarrow{A{B}'}=\overrightarrow{AB}+\overrightarrow{B{B}'} \\ & \overrightarrow{B{C}'}=\overrightarrow{BC}+\overrightarrow{C{C}'}=\overrightarrow{BC}+\overrightarrow{B{B}'} \\ \end{align} \right.\Rightarrow \overrightarrow{A{B}'}.\overrightarrow{B{C}'}=AB.BC.\cos {{120}^{0}}+B{{{B}'}^{2}}=\frac{3}{2}{{a}^{2}}.\) Suy ra \(\cos \left( A{B}';B{C}' \right)=\frac{\left| \overrightarrow{A{B}'}.\overrightarrow{B{C}'} \right|}{A{B}'.B{C}'}=\frac{\frac{3}{2}{{a}^{2}}}{\sqrt{A{{B}^{2}}+B{{{{B}'}}^{2}}}.\sqrt{B{{C}^{2}}+C{{{{C}'}}^{2}}}}=\frac{\frac{3}{2}{{a}^{2}}}{{{a}^{2}}+{{\left( a\sqrt{2} \right)}^{2}}}=\frac{1}{2}.\) Vậy góc giữa hai đường thẳng \(A{B}'\) và \(B{C}'\) bằng \({{60}^{0}}.\) Chọn D
Câu hỏi 8 : Chọn mệnh đề đúng trong các mệnh đề sau:
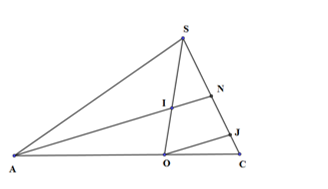
Đáp án: D Phương pháp giải: Lời giải chi tiết: Đáp án A hiển nhiên sai. Đáp án B: Ba đường thẳng phân biệt đôi một cắt nhau có thể đồng quy tại 1 điểm, khi đó chúng không nhất thiết đồng phẳng. Đáp án C: Ba đường thẳng đôi một cắt nhau thì có thể chúng đồng phẳng cắt nhau, không nhất thiết đồng quy. Chọn đáp án D. Câu hỏi 9 : Cho hình chóp \(S.ABCD\) có đáy là hình thang ABCD với \(AD//BC\) và \(AD = 2BC\). Gọi M là điểm trên cạnh SD thỏa mãn \(SM=\frac{1}{3}SD\). Mặt phẳng \(\left( {ABM} \right)\) cắt cạnh bên SC tại điểm N. Tính tỉ số \(\frac{{SN}}{{SC}}\).
Đáp án: A Phương pháp giải: Lời giải chi tiết:
Gọi O là giao điểm của AC và BD; I là giao điểm của SO và BM; N là giao điểm của AI và SC \( \Rightarrow I = \left( {ABM} \right) \cap SC\) Do ABCD là hình thang với \(AD//BC\) và \(AD = 2BC\), gọi O là giao điểm của AC và BD \( \Rightarrow \frac{{OC}}{{OA}} = \frac{{OB}}{{OD}} = \frac{{BC}}{{AD}} = \frac{1}{2} \Rightarrow \frac{{OA}}{{AC}} = \frac{{OD}}{{BD}} = \frac{2}{3}\) \( \Rightarrow OM//SB\) và \(\frac{{OM}}{{SB}} = \frac{2}{3}\) \( \Rightarrow \frac{{IO}}{{IS}} = \frac{{MO}}{{SB}} = \frac{2}{3}\) Kẻ \(OJ//AN,\,\left( {J \in AN} \right)\) Xét tam giác ANC có: \(OJ//AN,\,\,\frac{{OA}}{{AC}} = \frac{2}{3} \Rightarrow \frac{{NJ}}{{NC}} = \frac{2}{3}\,\, \Rightarrow \overrightarrow {NJ} = \frac{2}{3}\overrightarrow {NC} \) Xét tam giác ANC có: \(IN//OJ,\,\,\frac{{SI}}{{IO}} = \frac{3}{2} \Rightarrow \frac{{SN}}{{NJ}} = \frac{3}{2}\,\, \Rightarrow \overrightarrow {SN} = \frac{3}{2}\overrightarrow {NJ} \) \( \Rightarrow \overrightarrow {SN} = \overrightarrow {NC} \Rightarrow \overrightarrow {SN} = \frac{1}{2}\overrightarrow {SC} \Rightarrow \frac{{SN}}{{SC}} = \frac{1}{2}\). Chọn: A Câu hỏi 10 : Cho hình chóp S.ABCD có đáy ABCD là hình thang, đáy lớn là AB. Điểm M là trung điểm CD. Mặt phẳng \(\left( \alpha \right)\) qua M, song song với BC và SA. Mặt phẳng\(\left( \alpha \right)\) cắt AB tại E và cắt SB tại F. Thiết diện của hình chóp \(S.ABCD\) cắt bởi \(\left( \alpha \right)\) là hình gì?
Đáp án: C Phương pháp giải: Dựa vào yếu tố song song xác định thiết diện. Lời giải chi tiết:
Trong \(\left( {ABCD} \right)\) kẻ \(ME//CD,\,\left( {E \in AB} \right)\) Trong \(\left( {SAB} \right)\) kẻ \(EF//SA,\,\left( {F \in SB} \right)\) Trong \(\left( {SBC} \right)\) kẻ \(FK//BC,\,\left( {K \in SC} \right)\) Khi đó, \(\left( {MEFK} \right)\) là mặt phẳng qua M và song song với BC và SA\( \Rightarrow \left( {MEFK} \right) \equiv \left( \alpha \right)\) Thiết diện của hình chóp \(S.ABCD\) cắt bởi \(\left( \alpha \right)\) là tứ giác MEFK Ta có: \(KF//ME\left( {//BC} \right) \Rightarrow MEFK\)là hình thang Do \(MEBC\) là hình bình hành \( \Rightarrow ME = BC\) \(KF//BC \Rightarrow \frac{{KF}}{{BC}} = \frac{{SF}}{{SB}} < 1 \Rightarrow KF < BC \Rightarrow KF < ME\) \( \Rightarrow MEFK\)là hình thang có đáy lớn là ME. Chọn: C Câu hỏi 11 : Cho hình chóp S.ABCD có đáy ABCD là hình thang với đáy lớn AB. Gọi I, J lần lượt là trung điểm của AD, BC. Lấy G là trọng tâm tam giác SAB. Tìm điều kiện để thiết diện của hình chóp S.ABCD với mặt phẳng (IJG) là hình bình hành.
Đáp án: D Phương pháp giải: Lời giải chi tiết:
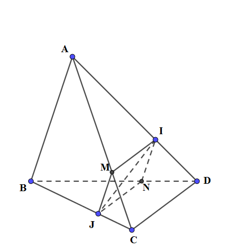
Ta có: \(\left( {IJG} \right) \cup \left( {SAB} \right) = EF,\,\,\left( {E \in SA,\,F \in SB} \right)\) và đi qua G, song song với AB // IJ Suy ra thiết diện là hình thang EFJI. Do G là trọng tâm tam giác SAB, EF // AB \( \Rightarrow EF = \frac{2}{3}AB\) Do IJ là đường trung bình của hình thang ABCD \( \Rightarrow IJ = \frac{{AB + CD}}{2}\) Để thiết diện là hình bình hành thì \(EF = IJ \Leftrightarrow \frac{2}{3}AB = \frac{1}{2}\left( {AB + CD} \right) \Leftrightarrow AB = 3CD\). Chọn: D Câu hỏi 12 : Cho tứ diện ABCD. Gọi I, J lần lượt thuộc các cạnh AD, BC sao cho IA = 2ID và JB = 2JC. Gọi (P) là mặt phẳng qua IJ và song song với AB. Thiết diện của mặt phẳng (P) và tứ diện ABCD là:
Đáp án: B Phương pháp giải: Xác định thiết diện của hình chóp cắt bởi mặt phẳng (P). Sử dụng định lí Ta-lét. Lời giải chi tiết:
Kẻ MJ // AB, \(M \in AC\); NI // AB \(N \in BD\) \( \Rightarrow M,N,I,J\) đồng phẳng và \(\left( {MINJ} \right) \equiv \left( P \right)\) Thiết diện của mặt phẳng (P) và tứ diện ABCD là tứ giác MINJ, có: \(MJ//NI\) và \(MJ = IN\) (do \(\frac{{MJ}}{{AB}} = \frac{{JC}}{{BC}} = \frac{1}{3},\,\,\frac{{IN}}{{AB}} = \frac{{ND}}{{BD}} = \frac{1}{3}\)) \( \Rightarrow MINJ\) là hình bình hành. Chọn: B Câu hỏi 13 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M, N, K lần lượt là trung điểm của các cạnh DC, BC, SA. Gọi H là giao điểm của AC và MN. Gọi (P) là mặt phẳng qua H, song song với CD và SB, thiết diện tạo bởi (P) và hình chóp S.ABCD là hình gì?
Đáp án: D Phương pháp giải: Nếu hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cùng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó. Lời giải chi tiết:
Trong (ABCD), dựng EF qua H song song CD \(\left( {E \in AD,\,\,F \in BC} \right)\) Trong (SBC) dựng GF // SB \(\left( {G \in SC} \right)\) Trong (SCD) dựng GP // CD \(\left( {P \in SD} \right)\) \( \Rightarrow PG//EF\left( {//CD} \right) \Rightarrow P,G,F,E\) đồng phẳng Ta có: \(\left( {EFGP} \right)//CD,\,\,\left( {EFGP} \right)//SB,\,\,H \in \left( {EFGP} \right)\) \( \Rightarrow \left( {EFGP} \right)\) trùng với (P) \( \Rightarrow \)Thiết diện tạo bởi (P) và hình chóp S.ABCD là tứ giác EFGP. Lại có, \(EF//PG \Rightarrow EFPG\) là hình thang. Chọn: D Câu hỏi 14 : Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC và AD. Gọi Q là giao điểm của CD và mặt phẳng (MNP). Tìm khẳng định sai ?
Đáp án: B Phương pháp giải: +) Xác định điểm Q. +) Sử dụng định lí : Giao tuyến của 3 mặt phẳng phân biệt hoặc đồng quy, hoặc đôi một song song. Lời giải chi tiết: (MNP) và (BCD) có N chung. \(\left\{ \begin{array}{l}MP \subset \left( {MNP} \right)\\BD \subset \left( {BCD} \right)\\MP//BD\end{array} \right. \Rightarrow \) Giao tuyến của 2 mặt phẳng (MNP) và (BCD) là đường thẳng đi qua N và song song với MP và BD. Trong (BCD) kẻ \(NQ//BD\,\,\left( {Q \in CD} \right) \Rightarrow Q = CD \cap \left( {MNP} \right)\). Ta có: \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {BCD} \right) = NQ\\\left( {MNPQ} \right) \cap \left( {ABD} \right) = MP\\\left( {ABD} \right) \cap \left( {BCD} \right) = BD\\MP//BD\end{array} \right. \Rightarrow MP//NQ//BD\) \( \Rightarrow \) D đúng. Ta có : \(MP//NQ;\,\,MP = NQ = \frac{1}{2}BD \Rightarrow MNPQ\) là hình bình hành\( \Rightarrow C\) đúng. \( \Rightarrow MN//PQ\). CMTT ta có MN // AC // PQ. Vậy đáp án B sai. Chọn B.
Câu hỏi 15 : Cho hình chóp S.ABCD có đáy ABCD là hình thang với AB // CD và \(AB = 2DC\). Gọi O là giao điểm của AC và BD, G là trọng tâm tam giác SBC, H là giao điểm của DG và (SAC). Tỉ số \(\dfrac{{GH}}{{GD}}\) bằng:
Đáp án: C Phương pháp giải: Áp dụng định lí Ta-lét. Lời giải chi tiết:
Gọi M là trung điểm của BC, \(I = AC \cap DM\). Trong (SDM) gọi \(H = DG \cap SI\) ta có: \(\begin{array}{l}I \in AC \Rightarrow I \in \left( {SAC} \right) \Rightarrow SI \subset SAC\\H \in SI \Rightarrow H \in \left( {SAC} \right) \Rightarrow H = DG \cap \left( {SAC} \right)\end{array}\). Gọi N là trung điểm của AD, \(E = AC \cap MN\) \( \Rightarrow MN\) là đường trung bình của hình thang ABCD \( \Rightarrow MN//AB//CD\) và \(MN = \dfrac{{AB + CD}}{2} = \dfrac{{2CD + CD}}{2} = \dfrac{{3CD}}{2}\). Áp dụng định lí Ta-lét ta có: \(\dfrac{{NE}}{{CD}} = \dfrac{{AN}}{{AD}} = \dfrac{1}{2} \Rightarrow NE = \dfrac{1}{2}CD \Rightarrow ME = \dfrac{3}{2}CD - \dfrac{1}{2}CD = CD\) \(\dfrac{{IM}}{{ID}} = \dfrac{{CD}}{{MN}} = \dfrac{{ME}}{{CD}} = 1 \Rightarrow IM = ID\). Kẻ \(GK//DM\), áp dụng định lí Vi-ét ta có : \(\dfrac{{GH}}{{DH}} = \dfrac{{KG}}{{ID}} = \dfrac{{KG}}{{IM}} = \dfrac{{KG}}{{IM}} = \dfrac{{SG}}{{SM}} = \dfrac{2}{3}\) \( \Rightarrow \dfrac{{GH}}{{GH + DH}} = \dfrac{2}{{2 + 3}} = \dfrac{2}{5} \Rightarrow \dfrac{{GH}}{{GD}} = \dfrac{2}{5}\). Chọn C. Câu hỏi 16 : Cho hình chóp S.ABCD có đáy ABCD là hình thang với các cạnh đáy AB, CD. Gọi I, J lần lượt là trung điểm của AD, BC và G là trọng tâm tam giác SAB. Điều kiện nào của AB và CD để thiết diện của hình chóp khi cắt bởi mặt phẳng (IJG) là hình bình hành?
Đáp án: D Phương pháp giải: Dựa vào các yếu tố song song xác định thiết diện. Lời giải chi tiết: Qua G dựng EF song song AB (\(E \in SB,F \in SA\)) IJ là đường trung bình của hình thang ABCD \( \Rightarrow \left\{ \begin{array}{l}IJ//AB//CD\\IJ = \dfrac{{AB + CD}}{2}\end{array} \right.\) Ta có: \(\left\{ \begin{array}{l}IJ//AB\\AB//EF\end{array} \right. \Rightarrow IJ//EF \Rightarrow I,J,E,F\) đồng phẳng \( \Rightarrow I,J,E,F,G\) đồng phẳng \( \Rightarrow \left( {GIJ} \right) \equiv \left( {IJEF} \right)\) Thiết diện của \(\left( {GIJ} \right)\) với hình chóp là hình thang \(IJEF,\,\left( {IJ//EF} \right)\) Để thiết diện là hình bình hành thì \(IJ = EF\)\( \Leftrightarrow \dfrac{{AB + CD}}{2} = \dfrac{2}{3}AB\) (do \(\dfrac{{EF}}{{AB}} = \dfrac{{SE}}{{SB}} = \dfrac{{SG}}{{SM}} = \dfrac{2}{3}\)) \( \Leftrightarrow 3AB + 3CD = 4AB \Leftrightarrow AB = 3CD\) Chọn: D Câu hỏi 17 : Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SD, điểm N thuộc cạnh SA sao cho SN = 3AN . Đường thẳng MN cắt mặt phẳng (ABCD) tại P, đường thẳng PC cắt cạnh AB tại K . Trình bày cách xác định điểm K và tính tỉ số \(\dfrac{{KA}}{{KB}}\).
Đáp án: C Phương pháp giải: Lời giải chi tiết:
Trong mp(SAD) gọi \(P = MN \cap AD\) Ta có: \(\left\{ \begin{array}{l}P \in MN\\P \in AD \subset \left( {ABCD} \right)\end{array} \right. \Rightarrow P = MN \cap \left( {ABCD} \right)\) Trong mp(ABCD) gọi \(K = PC \cap AB\). Khi đó điểm K là điểm cần dựng. Từ \(SA = 3AN\,\,\left( {gt} \right)\) suy ra \(AN = \dfrac{1}{4}SA\) Gọi E là trung điểm AD. Ta có ME là đường trung bình của tam giác SAD \( \Rightarrow ME//SA\) \( \Rightarrow AN//ME\). Áp dụng định lí Talet ta có : \(\dfrac{{PA}}{{PE}} = \dfrac{{AN}}{{ME}} = \dfrac{{\dfrac{1}{4}SA}}{{\dfrac{1}{2}SA}} = \dfrac{1}{2} \Rightarrow \dfrac{{PA}}{{PD}} = \dfrac{1}{3}\) Trong mặt phẳng (ABCD), có AK / / CD nên ta có: \(\dfrac{{AK}}{{CD}} = \dfrac{{PA}}{{PD}} = \dfrac{1}{3} \Rightarrow \dfrac{{AK}}{{AB}} = \dfrac{1}{3}\,\,\left( {do\,\,AB = CD} \right) \Rightarrow \dfrac{{AK}}{{BK}} = \dfrac{1}{2}\). Câu hỏi 18 : Cho hình hộp ABCD.A'B'C'D'. Gọi G và G' là trọng tâm các tam giác BDA' và A’CC’. Khẳng định nào sau đây đúng?
Đáp án: D Phương pháp giải: Sử dụng định lí Ta-lét. Lời giải chi tiết:
Gọi \(O = AC \cap BD,\,\,O' = A'C' \cap B'D',I = AC' \cap A'C\). Do ACC’A’ là hình bình hành => I là trung điểm của A’C \(\Rightarrow G \in AI \Rightarrow G \in AC'\). Chứng minh tương tự ta có \(G' \in AC'\). Do G là trọng tâm tam giác BDA’ nên \(\frac{{A'G}}{{OG}} = 2\). Áp dụng định lí Ta-lét ta có: \(\frac{{A'G}}{{OG}} = \frac{{GC'}}{{AG}} = 2 \Rightarrow AG = \frac{1}{3}AC'\). Chứng minh tương tự ta có \(G'C' = \frac{1}{3}AC'\). Vậy \(GG' = \frac{1}{3}AC'\). Chọn D. Câu hỏi 19 : Cho tứ diện \(ABCD\) có \(AB = CD = a.\) Gọi \(M,\;N\) lần lượt là trung điểm của \(AD\) và \(BC.\) Biết \(MN = \dfrac{{\sqrt 3 a}}{2},\) góc giữa đường thẳng\(AB\) và \(CD\) bằng:
Đáp án: C Phương pháp giải: Góc giữa hai đường thẳng \(a;\;b\) là góc giữa hai đường thẳng \(a',\;b'\) với \(a//a',\;\;b//b'.\) Công thức định lý hàm số cos trong \(\Delta ABC\) với các cạnh \(a,\;b,\;c\) là: \({a^2} = {b^2} + {c^2} - 2bc\cos A.\) Lời giải chi tiết:
Gọi P là trung điểm của AC ta có: PM // CD và PN // AB \( \Rightarrow \angle \left( {AB;CD} \right) = \angle \left( {PM;PN} \right)\). Do PM, PN lần lượt là đường trung bình của tam giác ACD và tam giác ABC \( \Rightarrow PM = \dfrac{{CD}}{2} = \dfrac{a}{2};\,\,PN = \dfrac{{AB}}{2} = \dfrac{a}{2}\) Xét tam giác PMN có: \(\cos \angle MPN = \dfrac{{P{M^2} + P{N^2} - M{N^2}}}{{2.PM.PN}} = \dfrac{{\dfrac{{{a^2}}}{4} + \dfrac{{{a^2}}}{4} - \dfrac{{3{a^2}}}{4}}}{{2.\dfrac{a}{2}.\dfrac{a}{2}}} = - \dfrac{1}{2} \Rightarrow \angle MPN = {120^0}\). Vậy \(\angle \left( {PM;PN} \right) = {180^0} - {120^0} = {60^0}\). Chọn C. Câu hỏi 20 : Cho tứ diện ABCD có \(AB=AC=AD= a,\) \(\widehat {BAC} = {60^0},\) \(\widehat {CAD} = {60^0},\) \(\widehat {DAB} = {90^0}.\) Khoảng cách giữa hai đường thẳng \(AC\) và \(BD\) là:
Đáp án: B Phương pháp giải: Sử dụng định lý Py-ta-go và hệ thức lượng trong tam giác vuông để làm bài toán. Lời giải chi tiết: Ta có: \(\angle BAC = \angle CAD = {60^0},\,\,AB = AC = AD = A\) \( \Rightarrow \Delta ABC,\,\,\,\Delta ACD\) đều \( \Rightarrow BC = CD = a.\) Có \(\angle BAD = {90^0} \Rightarrow BD = \sqrt {A{B^2} + A{{\rm{D}}^2}} = a\sqrt 2 .\) \( \Rightarrow \Delta BCD\) vuông cân tại \(C.\) Gọi \(H\) là trung điểm của \(BD.\) Kẻ \(KH \bot AC.\) \( \Rightarrow \left\{ \begin{array}{l}CH \bot BD\\AH \bot BD\end{array} \right. \Rightarrow BD \bot \left( {CAH} \right) \Rightarrow BD \bot KH\) \( \Rightarrow d\left( {AC,\,BD} \right) = KH.\) Xét \(\Delta AHC\) vuông tại \(H\) có đường cao \(KH\) ta có: \(KH = \frac{{HC.AH}}{{\sqrt {H{C^2} + H{A^2}} }} = \frac{{\frac{1}{4}B{D^2}}}{{\sqrt {\frac{1}{4}B{D^2} + \frac{1}{4}B{D^2}} }} = \frac{{\sqrt 2 }}{4}BD = \frac{{\sqrt 2 }}{4}.a\sqrt 2 = \frac{a}{2}.\) Chọn B. Câu hỏi 21 : Cho tứ diện đều \(ABCD\) có cạnh bằng \(a.\) Gọi M là trung điểm cạnh AB, \(\alpha \) là góc giữa hai đường thẳng BD và CM. Tính \(\cos \alpha \).
Đáp án: C Phương pháp giải: Gọi \(N\) là trung điểm của \(AD \Rightarrow \angle \left( {CM;BD} \right) = \angle \left( {CM;MN} \right)\). Lời giải chi tiết:
Gọi \(N\) là trung điểm của \(AD \Rightarrow MN//BD\). \( \Rightarrow \angle \left( {CM;BD} \right) = \angle \left( {CM;MN} \right)\). Dễ thấy \(\Delta ABC = \Delta ADC \Rightarrow CM = CN \Rightarrow \Delta CMN\) cân tại \(C\). Gọi \(H\) là trung điểm của \(MN \Rightarrow CH \bot MN\). Ta có: Tam giác \(ABC\) cân tại \(a \Rightarrow CM = \dfrac{{a\sqrt 3 }}{2}\). \(MN\) là đường trung bình của \(\Delta ABD \Rightarrow MN = \dfrac{1}{2}BD = \dfrac{a}{2}\). \( \Rightarrow MH = \dfrac{1}{2}MN = \dfrac{a}{4}\). Xét tam giác vuông \(CMH\) có: \(\cos \angle CMH = \dfrac{{MH}}{{CM}} = \dfrac{{\dfrac{a}{4}}}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{\sqrt 3 }}{6}\) . Vậy \(\cos \alpha = \dfrac{{\sqrt 3 }}{6}\). Chọn C. Câu hỏi 22 : Cho lăng trụ tam giác đều \(ABC.A'B'C'\) có đáy làm tam giác đều cạnh \(a,AA' = 2a\). Gọi \(\alpha \) là góc giữa \(AB'\) và \(BC'\). Tính \(\cos \alpha \).
Đáp án: D Phương pháp giải: - Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,BB',B'C'\). - Sử dụng tính chất góc giữa hai đường thẳng chéo nhau bằng góc giữa hai đường thẳng cùng thuộc 1 mặt phẳng mà lần lượt song song với hai đường thẳng đã cho. Lời giải chi tiết:
Gọi \(M,N,P\) lần lượt là trung điểm của \(AB,BB',B'C'\). Ta có: \(MN//AB'\) và \(NP//BC'\) (đường trung bình trong tam giác) Do đó góc giữa hai đường thẳng \(AB'\) và \(BC'\) bằng góc giữa hai đường thẳng \(MN\) và \(NP\). Gọi \(Q\) là trung điểm của \(A'B'\) thì \(MQ \bot \left( {A'B'C'} \right) \Rightarrow MQ \bot QP\). Tam giác \(MQP\) có \(MQ = AA' = 2a,\,\,QP = \dfrac{1}{2}A'C' = \dfrac{a}{2}\) \( \Rightarrow MP = \sqrt {M{Q^2} + Q{P^2}} = \sqrt {4{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt {17} }}{2}\) Lại có \(MN = \dfrac{1}{2}AB' = \dfrac{1}{2}\sqrt {A{B^2} + BB{'^2}} = \dfrac{1}{2}\sqrt {{a^2} + 4{a^2}} = \dfrac{{a\sqrt 5 }}{2}\); \(NP = \dfrac{1}{2}BC' = \dfrac{1}{2}\sqrt {BB{'^2} + B'C{'^2}} = \dfrac{1}{2}\sqrt {4{a^2} + {a^2}} = \dfrac{{a\sqrt 5 }}{2}\) Áp dụng định lý hàm số cô sin trong tam giác \(MNP\) ta có: \(\cos \widehat {MNP} = \dfrac{{M{N^2} + N{P^2} - M{P^2}}}{{2MN.NP}} = \dfrac{{\dfrac{{5{a^2}}}{4} + \dfrac{{5{a^2}}}{4} - \dfrac{{17{a^2}}}{4}}}{{2.\dfrac{{a\sqrt 5 }}{2}.\dfrac{{a\sqrt 5 }}{2}}} = - \dfrac{7}{{10}} < 0\) Do đó góc giữa hai đường thẳng \(MN\) và \(NP\) thỏa mãn \(\cos \widehat {\left( {MN,MP} \right)} = \dfrac{7}{{10}}\). Chọn D. Câu hỏi 23 : Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Tính khoảng cách giữa hai đường thẳng \(BC'\) và \(CD'\).
Đáp án: C Phương pháp giải: +) Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa đường này và mặt phẳng song song với nó chứa đường kia. +) Sử dụng phương pháp đổi đỉnh. Lời giải chi tiết: Ta có \(AD'//BC' \Rightarrow BC'//\left( {ACD'} \right)\) \( \Rightarrow d\left( {BC';CD'} \right) = d\left( {BC';\left( {ACD'} \right)} \right) = d\left( {B;\left( {ACD'} \right)} \right)\) . Gọi \(O = AC \cap BD\) ta có \(BD \cap \left( {ACD'} \right) = O\) \( \Rightarrow \dfrac{{d\left( {B;\left( {ACD'} \right)} \right)}}{{d\left( {D;\left( {ACD'} \right)} \right)}} = \dfrac{{BO}}{{DO}} = 1 \Rightarrow d\left( {B;\left( {ACD'} \right)} \right) = d\left( {D;\left( {ACD'} \right)} \right)\) Ta có \(\left\{ \begin{array}{l}AC \bot OD\\AC \bot DD'\end{array} \right. \Rightarrow AC \bot \left( {ODD'} \right)\). Trong \(\left( {ODD'} \right)\) kẻ \(DH \bot OD' \Rightarrow DH \bot AC\) \( \Rightarrow DH \bot \left( {ACD'} \right) \Rightarrow DH = d\left( {D;\left( {ACD'} \right)} \right)\) \(ABCD\) là hình vuông cạnh \(a \Rightarrow BD = a\sqrt 2 \Rightarrow OD = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}\). Áp dụng hệ thức lượng trong tam giác vuông \(ODD'\) ta có: \(DH = \dfrac{{DO.DD'}}{{\sqrt {D{O^2} + DD{'^2}} }} = \dfrac{{\dfrac{{a\sqrt 2 }}{2}.a}}{{\sqrt {\dfrac{{{a^2}}}{2} + {a^2}} }} = \dfrac{{a\sqrt 3 }}{3}\). Vậy \(d\left( {BC';CD'} \right) = \dfrac{{a\sqrt 3 }}{3}\). Chọn C. Câu hỏi 24 : Cho hình chóp tam giác \(S.ABC\) có đáy \(ABC\) là một tam giác vuông cân tại \(B\) với trọng tâm \(G\), cạnh bên \(SA\) tạo với đáy\(\left( {ABC} \right)\) một góc \({30^0}\). Biết hai mặt phẳng \(\left( {SBG} \right)\) và \(\left( {SCG} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABC} \right)\). Tính cosin của góc giữa hai đường thẳng \(SA\) và \(BC\).
Đáp án: C Phương pháp giải: +) Gọi \(M,\,\,N,\,\,P,\,\,Q\) lần lượt là trung điểm của \(AB,\,\,SC,\,\,BC,\,\,AC\). Chứng minh \(\angle \left( {SA;BC} \right) = \angle \left( {NQ;MQ} \right)\). +) Áp dụng định lí cosin trong tam giác \(MNQ\). Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}\left( {SBG} \right) \bot \left( {ABC} \right)\\\left( {SCG} \right) \bot \left( {ABC} \right)\\\left( {SBG} \right) \cap \left( {SCG} \right) = SG\end{array} \right. \Rightarrow SG \bot \left( {ABC} \right)\). Gọi \(M,\,\,N,\,\,P,\,\,Q\) lần lượt là trung điểm của \(AB,\,\,SC,\,\,BC,\,\,AC\). Đặt \(AB = BC = 1 \Rightarrow AC = \sqrt 2 \). Ta có: \(\angle \left( {SA;\left( {ABC} \right)} \right) = \angle \left( {SA;GA} \right) = \angle SAG = {30^0}\). Ta có \(NQ\) là đường trung bình của tamg giác \(SAC \Rightarrow NQ//SA\). \(MQ\) là đường trung bình của tam giác \(ABC \Rightarrow MQ//BC\). \( \Rightarrow \angle \left( {SA;BC} \right) = \angle \left( {NQ;MQ} \right)\).
Ta có: \(AP = \sqrt {1 + \frac{1}{4}} = \frac{{\sqrt 5 }}{2} = CM \Rightarrow AG = \frac{2}{3}AP = \frac{{\sqrt 5 }}{3}\). \( \Rightarrow SG = AG.\tan {30^0} = \frac{{\sqrt 5 }}{3}.\frac{{\sqrt 3 }}{3} = \frac{{\sqrt {15} }}{9};\,\,SA = \frac{{AG}}{{\cos {{30}^0}}} = \frac{{2\sqrt {15} }}{9}\). \( \Rightarrow NQ = \frac{1}{2}SA = \frac{{\sqrt {15} }}{9}\) và \(MQ = \frac{1}{2}BC = \frac{1}{2}\). Ta có \(MC = \frac{{\sqrt 5 }}{2} \Rightarrow GC = \frac{2}{3}MC = \frac{{\sqrt 5 }}{3};\,\,GM = \frac{1}{3}MC = \frac{{\sqrt 5 }}{6}\). Áp dụng định lí Pytago ta có: \(SC = \sqrt {S{G^2} + G{C^2}} = \frac{{2\sqrt {15} }}{9};\,\,SM = \sqrt {S{G^2} + G{M^2}} = \frac{{\sqrt {105} }}{{18}}\). Xét tam giác \(SMC\) ta có: \(M{N^2} = \frac{{S{M^2} + M{C^2}}}{2} - \frac{{S{C^2}}}{4} = \frac{{65}}{{108}} \Leftrightarrow MN = \frac{{\sqrt {195} }}{{18}}\). Áp dụng định lí cosin trong tam giác \(MNQ\) : \(\cos \angle MQN = \frac{{M{Q^2} + N{Q^2} - M{N^2}}}{{2.MQ.NQ}} = \frac{{\frac{1}{4} + \frac{5}{{27}} - \frac{{65}}{{108}}}}{{2.\frac{1}{2}.\frac{{\sqrt {15} }}{9}}} = \frac{{ - \frac{1}{6}}}{{\frac{{\sqrt {15} }}{9}}} = - \frac{{\sqrt {15} }}{{10}} < 0\). Vậy \(\cos \angle \left( {NQ;MQ} \right) = \frac{{15}}{{10}} = \cos \angle \left( {SA;BC} \right)\). Chọn C. Câu hỏi 25 : Cho tứ diện \(ABCD\) có \(AB = CD\) và \(AB \bot CD\). Gọi \(I,\,\,J,\,\,E,\,\,F\) lần lượt là trung điểm của \(AC,\,\,BC,\,\,BD,\,\,AD\) . Góc \(\left( {IE;IF} \right)\) bằng:
Đáp án: A Phương pháp giải: Chứng minh tứ giác \(IJEF\) là tứ giác đặc biệt. Lời giải chi tiết: Ta có \(IF\) là đường trung bình của tam giác \(ACD\); \(JE\) là đường trung bình của tam giác \(BCD\). \(\begin{array}{l} \Rightarrow IF//CD;\,\,JE//CD;\,\,IF = \dfrac{1}{2}CD;\,\,JE = \dfrac{1}{2}CD\\ \Rightarrow IF//JE;\,\,IF = JE\end{array}\) \( \Rightarrow IJEF\) là hình bình hành (Tứ giác có cặp cạnh đối song song bằng nhau). \(IJ\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow IJ = \dfrac{1}{2}AB = \dfrac{1}{2}CD = IF\). \(IJ//AB;\,\,IF//CD;\,\,AB \bot CD \Rightarrow IJ \bot IF\). \( \Rightarrow IJEF\) là hình vuông \( \Rightarrow \angle \left( {IE;IF} \right) = {45^0}\). Chọn A. Câu hỏi 26 : Cho tứ diện \(ABCD\) có \(AB = AC = AD\) và \(\widehat {BAC} = \widehat {BAD} = 60^\circ .\) Xác định góc giữa hai đường thẳng \(AB\) và \(CD.\)
Đáp án: A Phương pháp giải: Lấy \(N\) là trung điểm \(AB.\) Chứng minh \(AB \bot \left( {NCD} \right)\) từ đó suy ra góc giữa \(AB\) và \(CD.\) Lời giải chi tiết:
Các tam giác \(ABC\) và \(ABD\) đều là tam giác cân có 1 góc bằng \({60^0}\,\,\,\left( {gt} \right)\) nên \(\Delta ABC;\Delta ABD\) là các tam giác đều. Lấy \(N\) là trung điểm \(AB.\) Khi đó \(CN \bot AB;\,DN \bot AB\) (tính chất tam giác đều) \( \Rightarrow AB \bot \left( {DCN} \right) \Rightarrow AB \bot DC\) Nên góc giữa \(AB\) và \(CD\) là \(90^\circ .\) Chọn A. Câu hỏi 27 : Cho khối chóp S.ABC có \(\left( {SAB} \right) \bot \left( {ABC} \right),\)\(\left( {SAC} \right) \bot \left( {ABC} \right),SA = a,AB = AC = 2a,\) \(BC = 2a\sqrt 2 .\) Gọi M là trung điểm của BC. Khoảng cách giữa hai đường thẳng SM và AC bằng
Đáp án: B Phương pháp giải: Khoảng cách giữa hai đường thẳng chéo nhau là khoảng cách giữa đường này và mặt chứa đường kia Lời giải chi tiết: Xét tam giác \(ABC\) có \(A{B^2} + A{C^2} = 4{a^2} + 4{a^2} = 8{a^2} = B{C^2} \Rightarrow \Delta ABC\) vuông tại \(A\) (Định lí Pytago đảo). Gọi \(N\) là trung điểm của \(AB \Rightarrow MN//AC\) (MN là đường trung bình của tam giác ABC). \( \Rightarrow \left( {SMN} \right)//AC \Rightarrow d\left( {SM;AC} \right) = d\left( {AC;\left( {SMN} \right)} \right) = d\left( {A;\left( {SMN} \right)} \right)\). Ta có: \(\left\{ \begin{array}{l}MN//AC\\AB \bot AC\end{array} \right. \Rightarrow MN \bot AB\). \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAC} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {SAC} \right) = SA\end{array} \right. \Rightarrow SA \bot \left( {ABC} \right) \Rightarrow SA \bot MN\). \( \Rightarrow MN \bot \left( {SAB} \right)\). Trong \(\left( {SAB} \right)\) kẻ \(AH \bot SN\,\,\left( {H \in SN} \right)\) ta có: \(\left\{ \begin{array}{l}AH \bot SN\\AH \bot MN\end{array} \right. \Rightarrow AH \bot \left( {SMN} \right) \Rightarrow d\left( {A;\left( {SMN} \right)} \right) = AH\). Áp dụng hệ thức lượng trong tam giác vuông \(SAN\) ta có: \(AH = \frac{{SA.AN}}{{\sqrt {S{A^2} + A{N^2}} }} = \frac{{{a^2}}}{{a\sqrt 2 }} = \frac{{a\sqrt 2 }}{2}\). Vậy \(d\left( {SM;AC} \right) = \frac{{a\sqrt 2 }}{2}\). Chọn B. Câu hỏi 28 : Cho hình chóp \(S.ABCD\) có đáy là hình vuông \(ABCD\) cạnh bằng \(a\) và các cạnh bên đều bằng \(a\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AD\) và \(SD\). Số đo của góc \(\left( {MN;SC} \right)\) bằng:
Đáp án: C Phương pháp giải: Chứng minh \(\angle \left( {MN;SC} \right) = \angle \left( {SA;SC} \right)\). Lời giải chi tiết: Ta thấy \(MN\) là đường trung bình của tam giác \(SAD\). \( \Rightarrow MN//SA \Rightarrow \angle \left( {MN;SC} \right) = \angle \left( {SA;SC} \right)\). \(ABCD\) là hình vuông cạnh \(a \Rightarrow AC = a\sqrt 2 \). Lại có \(SA = SC = a \Rightarrow S{A^2} + S{C^2} = A{C^2} = 2{a^2} \Rightarrow \Delta SAC\) vuông cân tại \(S\). \( \Rightarrow \angle ASC = {90^0}\). Vậy \(\angle \left( {MN;SC} \right) = {90^0}\). Chọn C. Câu hỏi 29 : Cho tứ diện gần đều \(ABCD\), biết \(AB = CD = 5,AC = BD = \sqrt {34} ,AD = BC = \sqrt {41} \). Tính sin của góc giữa hai đường thẳng \(AB\) và \(CD\).
Đáp án: A Phương pháp giải: Lời giải chi tiết:
Gọi I, J, K, P lần lượt là trung điểm của AD, AC, BC, BD. Khi đó, AB // IP // JK, CD // IJ // KP \( \Rightarrow \) \(\left( {\widehat {AB;CD}} \right) = \left( {\widehat {IP;KP}} \right)\) Ta có: \(KP = \dfrac{1}{2}CD = \dfrac{5}{2}\), \(IP = \dfrac{1}{2}AB = \dfrac{5}{2}\) \(A{K^2} = \dfrac{{A{B^2} + A{C^2}}}{2} - \dfrac{{B{C^2}}}{4} = \dfrac{{25 + 34}}{2} - \dfrac{{41}}{4} = \dfrac{{77}}{4} = D{K^2}\) Tam giác \(AKD\) cân tại K, \(KI\) là trung tuyến \( \Rightarrow KI \bot AD \Rightarrow I{K^2} = A{K^2} - A{I^2} = \dfrac{{77}}{4} - \dfrac{{41}}{4} = 9\) \(\cos \widehat {IPK} = \dfrac{{I{P^2} + K{P^2} - I{K^2}}}{{2.IP.KP}} = \dfrac{{\dfrac{{25}}{4} + \dfrac{{25}}{4} - 9}}{{2.\dfrac{5}{2}.\dfrac{5}{2}}} = \dfrac{7}{{25}} > 0 \Rightarrow \widehat {IPK} < {90^0}\) \( \Rightarrow \left( {\widehat {AB;CD}} \right) = \left( {\widehat {IP;KP}} \right) = \widehat {IPK} \Rightarrow \sin \left( {\widehat {AB;CD}} \right) = \sin \widehat {IPK} = \sqrt {1 - {{\left( {\dfrac{7}{{25}}} \right)}^2}} = \dfrac{{24}}{{25}}\). Chọn: A Câu hỏi 30 : Cho hình chóp \(S.ABCD\) có đáy là hình bình hành (tham khảo hình vẽ). Một mặt phẳng đồng thời song song với \(AC\) và \(SB\) lần lượt cắt các đoạn thẳng \(SA,AB,BC,SC,SD,BD\) tương ứng tại \(M,N,E,F,I,J\). Có bao nhiêu khẳng định sai trong các khẳng định sau?
I) \(IJ//SB\) II) \(MF//AC\) III) Tứ giác \(MNEF\) là hình bình hành.
Đáp án: C Phương pháp giải: Dựng hình và nhận xét. Lời giải chi tiết:
Lấy \(M\) bất kì thuộc \(SA\). Trong \(\left( {SAB} \right)\), kẻ \(MN//SB\left( {N \in AB} \right)\). Trong \(\left( {ABCD} \right)\), kẻ \(NE//AC\left( {E \in BC} \right)\). Trong \(\left( {SBC} \right)\), kẻ \(EF//SB\left( {F \in SC} \right)\). Trong \(\left( {ABCD} \right)\), gọi \(NE \cap BD = J\). Trong \(\left( {SBD} \right)\), kẻ \(JI//SB\left( {I \in SD} \right)\). Từ đó ta được mặt phẳng \(\left( {MNEFI} \right)\) thỏa mãn bài toán và các điểm \(M,N,E,F,J,I\). Dễ thấy, \(SB//JI\) nên \(\left( I \right)\) đúng. \(MF//AC\) nên \(\left( {II} \right)\) đúng. Tứ giác \(MNEF\) có \(NE//MF\) (cùng \(//AC\)) và \(FE//MN\) (cùng song song \(SB\)) nên tứ giác \(MNEF\) là hình bình hành. Vậy cả ba khẳng định đều đúng. Chọn C Câu hỏi 31 : Cho hình hộp \(ABCD.A'B'C'D'\) (tham khảo hình vẽ). Hai điểm \(M,N\) lần lượt nằm trên hai cạnh \(AD,CC'\) sao cho \(AM = \dfrac{1}{2}AD,CN = \dfrac{1}{4}CC'\). Thiết diện của hình hộp cắt bởi mặt phẳng chứa đường thẳng \(MN\) và song song với mặt phẳng \(\left( {ACB'} \right)\) là
Đáp án: D Phương pháp giải: Chứng minh \(MN\) cắt mặt phẳng \(\left( {ACB'} \right)\) dẫn đến không có mặt phẳng cần tìm. Lời giải chi tiết:
Qua \(N\) kẻ \(NE//BC\left( {E \in BB'} \right)\), \(NE \cap B'C = K\). Dễ thấy \(NE//BC//AD\) nên các điểm \(A,M,N,E\) cùng thuộc mặt phẳng \(\left( {ADNE} \right)\). Lại có \(K = NE \cap CB'\)\( \Rightarrow K \in CB' \subset \left( {ACB'} \right) \Rightarrow AK \subset \left( {ACB'} \right)\) Trong mặt phẳng \(\left( {ADMN} \right)\) gọi \(H = MN \cap AK \Rightarrow \left\{ \begin{array}{l}H \in MN\\H \in AK \subset \left( {ACB'} \right)\end{array} \right.\)\( \Rightarrow H = MN \cap \left( {ACB'} \right)\) Do đó không có mặt phẳng nào chứa \(MN\) và song song \(\left( {ACB'} \right)\). Vậy không có thiết diện cần tìm. Chọn D Câu hỏi 32 : Cho hình hộp \(ABCD.A'B'C'D'\) (tham khảo hình vẽ). Gọi \(M\) là trung điểm cạnh \(A'D'\) và \(\left( \alpha \right)\) là mặt phẳng đi qua \(M\), song song với các đường thẳng \(BB',AC.\) Gọi \(T\) là giao điểm của đường thẳng \(BC\) và mặt phẳng \(\left( \alpha \right)\). Tính tỉ số \(\dfrac{{TB}}{{TC}}.\)
Đáp án: C Phương pháp giải: + Dựng mặt phẳng \(\left( \alpha \right)\) dựa vào mối quan hệ song song với \(BB',AC\) + Từ đó tính tỉ số \(\dfrac{{TB}}{{TC}}\) Lời giải chi tiết:
Gọi \(N,E\) lần lượt là trung điểm của \(AD,DC\) Ta có \(MN//AA'//BB'\) và \(NE//AC\) (do \(NE\) là đường trung bình của tam giác \(DAC\)) Suy ra \(\left( \alpha \right) \equiv \left( {MNE} \right)\) Trong \(\left( {ABCD} \right)\), kéo dài \(NE\) cắt \(BC\) tại \(T\). Suy ra \(ANTC\) là hình bình hành (do \(AN//TC;NT//AC\)) Do đó \(TC = AN = \dfrac{1}{2}AD = \dfrac{1}{2}BC\) Ta có \(\left( {MNE} \right) \cap BC = \left\{ T \right\}\) nên \(\dfrac{{TB}}{{TC}} = \dfrac{{\dfrac{3}{2}BC}}{{\dfrac{1}{2}BC}} = 3\) Chọn C Câu hỏi 33 : Cho tứ diện \(ABCD\) có \(BC = 9,AC = 6\) và \(BD = 3\) (tham khảo hình vẽ). Điểm \(M\) di chuyển trên cạnh \(BC.\) Mặt phẳng \(\left( \alpha \right)\) qua \(M,\) song song với \(AC\) và \(BD\) cắt tứ diện theo thiết diện là một tứ giác. Khi \(M\) di chuyển đến vị trí \({M_0}\) để thiết diện đó là một hình thoi, hãy tính tích \({M_0}B.{M_0}C.\)
Đáp án: C Phương pháp giải: + Dựng mặt phẳng \(\left( \alpha \right)\) theo mối quan hệ song song với \(AC,BD\) + Tìm thiết diện của mặt phẳng \(\left( \alpha \right)\) với hình chóp + Dựa vào điều kiện hình thoi và định lý Ta-lét để tính toán. Lời giải chi tiết:
Trong \(\left( {ABC} \right)\) kẻ \(MH//AC\left( {H \in AB} \right)\) Trong \(\left( {BCD} \right)\) kẻ \(ME//DB\left( {E \in DC} \right)\) Trong \(\left( {ABD} \right)\) kẻ \(HN//AD\left( {N \in AD} \right)\) Suy ra \(HN//ME\). Theo định lý Ta-lét ta có : \(\dfrac{{HN}}{{BD}} = \dfrac{{AH}}{{AB}} = \dfrac{{MC}}{{BC}} = \dfrac{{ME}}{{BD}} \Rightarrow HN = ME\) Từ đó \(MENH\) là hình bình hành. Ta có \(\left( \alpha \right) \equiv \left( {MENH} \right)\) và \(\left\{ \begin{array}{l}\left( {MENH} \right) \cap \left( {ABC} \right) = MH\\\left( {MENH} \right) \cap \left( {BCD} \right) = ME\\\left( {MENH} \right) \cap \left( {ABD} \right) = NH\\\left( {MENH} \right) \cap \left( {ACD} \right) = NE\end{array} \right.\) nên thiết diện cần tìm là hình bình hành \(MENH\) Để \(MENH\) là hình thoi thì \(MH = ME\) + Giả sử \(MC = a\left( {0 < a < 9} \right) \Rightarrow MB = 9 - a\) Theo định lý Ta-lét ta có \(\dfrac{{ME}}{{BD}} = \dfrac{{MC}}{{BC}} \Leftrightarrow \dfrac{{ME}}{3} = \dfrac{a}{9} \Leftrightarrow ME = \dfrac{a}{3}\) Theo định lý Ta-lét ta có \(\dfrac{{MH}}{{AC}} = \dfrac{{BM}}{{BC}} \Leftrightarrow \dfrac{{MH}}{6} = \dfrac{{9 - a}}{9} \Leftrightarrow MH = \dfrac{{18 - 2a}}{3}\) Mà \(ME = MH \Leftrightarrow \dfrac{a}{3} = \dfrac{{18 - 2a}}{3} \Leftrightarrow a = 18 - 2a \Leftrightarrow a = 6\) Suy ra \({M_0}C = 6;{M_0}B = 3 \Rightarrow {M_0}B.{M_0}C = 6.3 = 18\) Chọn C Câu hỏi 34 : Trong mặt phẳng \(\left( P \right)\) cho hình bình hành \(ABCD\). Gọi \(Ax,\,\,By,\,\,Cz,\,\,Dt\) lần lượt là các đường thẳng song song với nhau đi qua \(A,\,\,B,\,\,C,\,\,D\) và nằm về cùng một phía của măt phẳng \(\left( P \right)\) đồng thời không nằm trong \(\left( P \right)\). Một mặt phẳng \(\left( \alpha \right)\) lần lượt cắt \(Ax,\,\,By,\,\,Cz,\,\,Dt\) tại \(A',\,\,B',\,\,C',\,\,D'\) biết \(BB' = 5,2\,\,cm\), \(CC' = 8,6\,\,cm\) , \(DD' = 7,8\,\,cm\). Tính \(AA'\).
Đáp án: D Phương pháp giải: Dựa vào tính chất đường trung bình của hình thang. Lời giải chi tiết:
Do \(Ax,\,\,By,\,\,Cz,\,\,Dt\) song song với nhau cắt mặt phẳng \(\left( \alpha \right)\) lần lượt tại\(A',\,\,B',\,\,C',\,\,D'\) nên \(A'B'C'D'\) là hình bình hành và có tâm là \(O'\). Gọi \(O\) là tâm hình bình hành \(ABCD\). Ta có \(OO'\) là đường trung bình của hình thang \(BDD'B',\,\,ACC'A'\). \(\begin{array}{l} \Rightarrow \dfrac{{A'A + CC'}}{2} = O'O = \dfrac{{BB' + D'D}}{2}\\ \Leftrightarrow A'A + CC' = BB' + D'D\\ \Leftrightarrow A'A = 5,2 + 7,8 - 8,6 = 4,4cm\end{array}\) Chọn D. Câu hỏi 35 : Cho hình chóp \(S.ABCD\) đáy là hình bình hành tâm \(O\). Gọi \(M,\,\,N,\,\,P\) lần lượt là trung điểm của \(SA\), \(SC,\) \(OB\). Gọi \(Q\) là giao điểm của \(SD\) với \(mp\left( {MNP} \right)\). Tính \(\dfrac{{SQ}}{{SD}}.\)
Đáp án: A Phương pháp giải: Tìm điểm Q.\(\) Sử dụng định lí Menelaus để tính tỉ số. Lời giải chi tiết: Trong \(\left( {ABCD} \right)\) lấy \(PH\parallel MN\)\((H \in CD)\) Trong \(\left( {SCD} \right)\) gọi \(Q = NH \cap SD\) Áp dụng định lí Menelaus trong tam giác \(SCD\) với cát tuyến \(QNH\) ta có: \(\dfrac{{HD}}{{HC}}.\dfrac{{NC}}{{NS}}.\dfrac{{QS}}{{QD}} = 1\) Mà \(N\) là trung điểm của \(SC \Rightarrow \dfrac{{NC}}{{NS}} = 1\). Mặt khác áp dụng định lí Ta-lét trong tam giác \(DPH\) ta có \(\dfrac{{HD}}{{HC}} = \dfrac{{DP}}{{OP}} = 3\)(vì \(P\) là trung điểm của \(OB\)). Do đó ta có \(\dfrac{{QS}}{{QD}} = \dfrac{1}{3} \Rightarrow \dfrac{{SQ}}{{SD}} = \dfrac{1}{4}\) Chọn A. Trong \(\left( {ABCD} \right)\) lấy \(PH\parallel MN\)\((H \in CD)\) Trong \(\left( {SCD} \right)\) gọi \(Q = NH \cap SD\) Áp dụng định lí Menelaus trong tam giác \(SCD\) với cát tuyến \(QNH\) ta có: \(\dfrac{{HD}}{{HC}}.\dfrac{{NC}}{{NS}}.\dfrac{{QS}}{{QD}} = 1\) Mà \(N\) là trung điểm của \(SC \Rightarrow \dfrac{{NC}}{{NS}} = 1\). Mặt khác áp dụng định lí Ta-lét trong tam giác \(DPH\) ta có \(\dfrac{{HD}}{{HC}} = \dfrac{{DP}}{{OP}} = 3\)(vì \(P\) là trung điểm của \(OB\)). Do đó ta có \(\dfrac{{QS}}{{QD}} = \dfrac{1}{3} \Rightarrow \dfrac{{SQ}}{{SD}} = \dfrac{1}{4}\) Chọn A. Câu hỏi 36 : Cho tứ diện \(ABCD\) có\(AC = a,\,\,BD = 3a\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(AD\) và \(BC.\) Biết \(AC\) vuông góc với\(BD\). Tính độ dài đoạn thẳng \(MN\) theo \(a.\)
Đáp án: C Phương pháp giải: - Gọi \(P\) là trung điểm của \(AB\). Tính \(PM,\,\,PN\). - Chứng minh \(\Delta PMN\) vuông, áp dụng định lí Pytago tính \(MN\). Lời giải chi tiết:
Gọi \(P\) là trung điểm của \(AB\). Ta có: \(PM,\,\,PN\) lần lượt là đường trung bình của \(\Delta ACD,\,\,\Delta ABC\) nên \(PM = \dfrac{1}{2}BD = \dfrac{{3a}}{2}\), \(PN = \dfrac{1}{2}AC = \dfrac{a}{2}\) và \(\left\{ \begin{array}{l}PM\parallel BD\\PN\parallel AC\end{array} \right.\). Mà \(AC \bot BD\,\,\left( {gt} \right)\) nên \(PM \bot PN\), do đó tam giác \(PMN\) vuông tại \(P\). Áp dụng định lí Pytago ta có: \(MN = \sqrt {P{M^2} + P{N^2}} \) \( = \sqrt {\dfrac{{9{a^2}}}{4} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt {10} }}{2}\). Chọn C. Câu hỏi 37 : Cho tứ diện \(ABCD\). Gọi \(M,\,N\)lần lượt là trung điểm của các cạnh \(AB\), \(CD\). \(G\)là trung điểm của \(MN\), \(I\)là giao điểm của đường thẳng \(AG\)và mặt phẳng \(\left( {BCD} \right)\). Tính tỉ số \(\dfrac{{GI}}{{GA}}\)?
Đáp án: D Phương pháp giải: Vẽ hình sau đó sử dụng định lý Ta-lét trong tam giác. Lời giải chi tiết:
Trog \(\left( {ABN} \right)\) qua \(M\)kẻ đường thẳng song song với \(AI\) cắt \(BN\) tại \(J\). Xét tam giác \(MNJ\) ta có: \(\left\{ \begin{array}{l}GI//MJ\\GN = GM\,\left( {gt} \right)\end{array} \right. \Rightarrow GI = \dfrac{1}{2}.MJ\,\,\,\,\left( 1 \right)\) Xét tam giác \(BAI\) ta có: \(\left\{ \begin{array}{l}MJ//AI\\MA = MB\end{array} \right. \Rightarrow MJ = \dfrac{1}{2}.AI\,\,\,\left( 2 \right)\) Từ \(\left( 1 \right)\& \left( 2 \right) \Rightarrow GI = \dfrac{1}{4}.AI \Leftrightarrow \dfrac{{GI}}{{GA}} = \dfrac{1}{3}.\) Chọn D. Câu hỏi 38 : Cho tứ diện \(ABCD\) có \(AB = CD = a\), \(EF = \dfrac{{a\sqrt 3 }}{2}\) (\(E,\,\,F\) lần lượt là trung điểm của \(BC\) và\(AD\)). Số đo góc giữa hai đường thẳng \(AB\) và \(CD\) là:
Đáp án: C Phương pháp giải: - \(\left\{ \begin{array}{l}a\parallel a'\\b\parallel b'\end{array} \right. \Rightarrow \angle \left( {a;b} \right) = \angle \left( {a';b'} \right)\). - Sử dụng định lí Cosin trong tam giác. Lời giải chi tiết:
Gọi \(G\) là trung điểm của \(AC\). Vì \(EG,\,\,FG\) lần lượt là đường trung bình của tam giác \(ABC\) và \(ACD\) nên \(EG\parallel AB,\,\,FG\parallel CD\) (tính chất đường trung bình). Do đó \(\angle \left( {AB;CD} \right) = \angle \left( {EG;FG} \right)\). Ta có: \(EG = \dfrac{1}{2}AB = \dfrac{a}{2}\), \(FG = \dfrac{1}{2}CD = \dfrac{a}{2}\). Áp dụng định lí Cosin trong ta giác \(GEF\) ta có: \(\begin{array}{l}\cos \angle EGF = \dfrac{{G{E^2} + G{F^2} - E{F^2}}}{{2GE.GF}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\dfrac{{{a^2}}}{4} + \dfrac{{{a^2}}}{4} - \dfrac{{3{a^2}}}{4}}}{{2.\dfrac{a}{2}.\dfrac{a}{2}}} = - \dfrac{1}{2}\end{array}\) \( \Rightarrow \angle EGF = {120^0}\) \(\angle \left( {GE;GF} \right) = {180^0} - {120^0} = {60^0}\). Vậy \(\angle \left( {AB;CD} \right) = {60^0}\). Chọn C. Câu hỏi 39 : Cho hình chóp S.ABC có A’, B’ lần lượt là trung điểm SA, SB, G là trọng tâm tam giác ABC. C’ là điểm di động trên cạnh SC. Gọi G’ là giao điểm của SG với (A’B’C’). Khi C’ di động trên SC, biểu thức nào sau đây có giá trị không thay đổi?
Đáp án: D Phương pháp giải: Áp dụng định lí Menelaus trong tam giác. Cho tam giác ABC, một đường thẳng d cắt BC, AC, AB lần lượt tại A’, B’, C’, khi đó ta có: \(\dfrac{{A'B}}{{A'C}}.\dfrac{{B'C}}{{B'A}}.\dfrac{{C'A}}{{C'B}} = 1\).
Lời giải chi tiết:
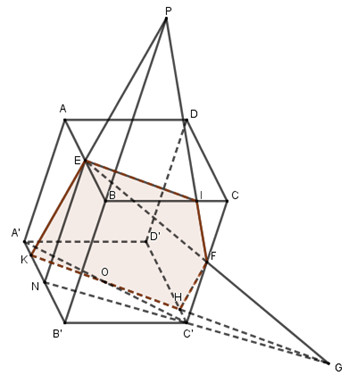
Gọi P là trung điểm của SC, \(N = M'P \cap SG\). Ta dễ dàng chứng minh được N là trung điểm của SG. Áp dụng định lí Menelaus trong tam giác SNP có : \(\dfrac{{G'S}}{{G'N}}.\dfrac{{M'N}}{{M'P}}.\dfrac{{C'P}}{{C'S}} = 1\,\,\,\left( * \right)\). Áp dụng định lí Ta-lét ta có : \(\dfrac{{M'N}}{{MG}} = \dfrac{1}{2};\,\,\dfrac{{NP}}{{GC}} = \dfrac{1}{2} \Leftrightarrow \dfrac{{M'N}}{{MG}} = \dfrac{{NP}}{{GC}} \Rightarrow \dfrac{{M'N}}{{NP}} = \dfrac{{MG}}{{GC}} = \dfrac{1}{2} \Rightarrow \dfrac{{M'N}}{{M'P}} = \dfrac{1}{3}\) Thay vào (*) ta có \(\dfrac{{G'S}}{{G'N}}.\dfrac{1}{3}.\dfrac{{C'P}}{{C'S}} = 1 \Leftrightarrow \dfrac{{G'S}}{{G'N}}.\dfrac{{C'P}}{{C'S}} = 3 \Leftrightarrow \dfrac{{C'P}}{{C'S}} = 3.\dfrac{{G'N}}{{G'S}}\,\,\,\left( {**} \right)\). Ta có : \(\begin{array}{l}\dfrac{{G'S}}{{G'N}} = \dfrac{{NG'}}{{SG'}} = \dfrac{{SN - SG'}}{{SG'}} = \dfrac{{\dfrac{1}{2}SG}}{{SG'}} - 1 = \dfrac{1}{2}\dfrac{{SG}}{{SG'}} - 1\\\dfrac{{C'P}}{{C'S}} = \dfrac{{PC'}}{{SC'}} = \dfrac{{SP - SC'}}{{SC'}} = \dfrac{{\dfrac{1}{2}SC}}{{SC'}} - 1 = \dfrac{1}{2}\dfrac{{SC}}{{SC'}} - 1\end{array}\) Thay vào (**) \( \Rightarrow \dfrac{1}{2}\dfrac{{SC}}{{SC'}} - 1 = 3\left( {\dfrac{1}{2}\dfrac{{SG}}{{SG'}} - 1} \right) \Leftrightarrow \dfrac{1}{2}\left( {3\dfrac{{SG}}{{SG'}} - \dfrac{{SC}}{{SC'}}} \right) = 2 \Leftrightarrow 3\dfrac{{SG}}{{SG'}} - \dfrac{{SC}}{{SC'}} = 4 = const\). Chọn D. Câu hỏi 40 : Gọi \(N\) là trung điểm của \(A'B'\), \(G\) là giao điểm của \(NC'\) với \(EF\). Từ đó mở rộng mặt phẳng \(\left( {FOE} \right)\) rồi tìm giao tuyến của \(\left( {FOE} \right)\) với các mặt của hình hộp. Phương pháp giải: Lời giải chi tiết:
Gọi \(N\) là trung điểm của \(A'B'\)\( \Rightarrow NE//FC'\) nên bốn điểm \(N,E,F,C\) đồng phẳng. Trong \(\left( {NEFC} \right)\), gọi \(G = NC' \cap EF \Rightarrow G \in EF \subset \left( {FOE} \right)\). Trong \(\left( {A'B'C'D'} \right)\), gọi \(H,K\) lần lượt là giao điểm của \(GO\) với \(D'C',A'B'\) Khi đó \(\left( {FOE} \right) \equiv \left( {GKE} \right)\). Trong \(\left( {ABB'A'} \right)\), gọi \(P = KE \cap B'B\) \( \Rightarrow P \in BB' \subset \left( {BCC'B'} \right)\) Trong \(\left( {BCC'B'} \right)\), gọi \(I = PF \cap BC\) \( \Rightarrow \left\{ \begin{array}{l}I \in BC\\I \in PF \subset \left( {GKE} \right) \equiv \left( {FOE} \right)\end{array} \right.\) \( \Rightarrow I = BC \cap \left( {FOE} \right)\). Khi đó \(\begin{array}{l}\left( {FOE} \right) \cap \left( {A'B'C'D'} \right) = HK\\\left( {FOE} \right) \cap \left( {ABB'A'} \right) = KE\\\left( {FOE} \right) \cap \left( {ABCD} \right) = EI\\\left( {FOE} \right) \cap \left( {BCC'B'} \right) = IF\\\left( {FOE} \right) \cap \left( {DCC'D'} \right) = FH\end{array}\) Thiết diện là ngũ giác \(EIFHK\). Ta có, \(\dfrac{{IB}}{{IC}} = \dfrac{{PB}}{{CF}}\), \(CF = \dfrac{1}{2}CC'\) \( \Rightarrow \dfrac{{PB}}{{CF}} = \dfrac{{PB}}{{\dfrac{1}{2}CC'}} = 2.\dfrac{{PB}}{{BB'}}\) \(HC'//KN \Rightarrow \dfrac{{HC'}}{{KN}} = \dfrac{{GC'}}{{GN}}\) Mà \(C'F//NE \Rightarrow \dfrac{{GC'}}{{GN}} = \dfrac{{C'F}}{{NE}} = \dfrac{1}{2}\) \( \Rightarrow \dfrac{{HC'}}{{KN}} = \dfrac{1}{2} \Rightarrow \dfrac{{A'K}}{{KN}} = \dfrac{1}{2}\) \( \Rightarrow \dfrac{{A'K}}{{A'N}} = \dfrac{1}{3} \Rightarrow \dfrac{{A'K}}{{A'B'}} = \dfrac{1}{6}\) \( \Rightarrow \dfrac{{KN}}{{A'N}} = \dfrac{2}{3} = \dfrac{{K'N}}{{NB'}} \Rightarrow \dfrac{{K'N}}{{KB'}} = \dfrac{2}{5}\) \( \Rightarrow \dfrac{{NE}}{{PB'}} = \dfrac{2}{5} \Rightarrow \dfrac{{BB'}}{{PB'}} = \dfrac{2}{5}\) \( \Rightarrow \dfrac{{PB}}{{PB'}} = \dfrac{3}{5} \Rightarrow \dfrac{{PB}}{{BB'}} = \dfrac{3}{2}\) Vậy \(\dfrac{{IB}}{{IC}} = \dfrac{{PB}}{{CF}} = 2.\dfrac{{PB}}{{BB'}} = 2.\dfrac{3}{2} = 3\).
|