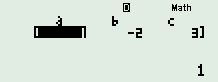
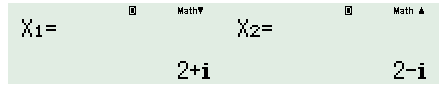30 bài tập phương trình bậc hai với hệ số thực mức độ nhận biếtLàm bàiCâu hỏi 1 : Các nghiệm của phương trình: \({{z}^{2}}-(3-i)z+4-3i=0\) là:
Đáp án: A Phương pháp giải: Phương pháp giải phương trình bậc hai trên tập số phức: \(a{{x}^{2}}+bx+c=0\left( a\ne 0,a,b,c\in C \right)\) - Tính \(\Delta ={{b}^{2}}-4ac\). - Tìm một căn bậc hai của \(\Delta \). - Áp dụng công thức nghiệm \({{x}_{1,2}}=\frac{-b\pm \sqrt{\Delta }}{2a}\). Lời giải chi tiết: Phương trình: \({{z}^{2}}-(3-i)z+4-3i=0\) Có: \(\Delta ={{\left( 3-i \right)}^{2}}-4(4-3i)=9-6i+{{i}^{2}}-16+12i\) \(=-8+6i=1+2.3i+9{{i}^{2}}={{\left( 1+3i \right)}^{2}}\) \(\Rightarrow \sqrt{\Delta }=\sqrt{{{\left( 1+3i \right)}^{2}}}=\left| 1+3i \right|\) Phương trình có \(2\) nghiệm là: \({{z}_{1}}=\frac{3-i-1-3i}{2}=1-2i\);\({{z}_{2}}=\frac{3-i+1+3i}{2}=2+i\) Chọn A Câu hỏi 2 : Các nghiệm \({{z}_{1}}=\frac{-1-5i\sqrt{5}}{3};{{z}_{2}}=\frac{-1+5i\sqrt{5}}{3}\) là nghiệm của phương trình nào sau đây:
Đáp án: B Phương pháp giải: Nếu có \({{z}_{1}}+{{z}_{2}}=S;{{z}_{1}}.{{z}_{2}}=P\) thì \({{z}_{1}},{{z}_{2}}\) là nghiệm của phương trình bậc hai \({{z}^{2}}-Sz+P=0\). Lời giải chi tiết: Ta có: \({{z}_{1}}+{{z}_{2}}=\frac{-1-5i\sqrt{5}}{3}+\frac{-1+5i\sqrt{5}}{3}=\frac{-2}{3}\) \({{z}_{1}}.{{z}_{2}}=\frac{-1-5i\sqrt{5}}{3}.\frac{-1+5i\sqrt{5}}{3}=\frac{126}{9}=\frac{42}{3}\) \(\Rightarrow {{z}_{1}};{{z}_{2}}\) là các nghiệm của phương trình: \({{z}^{2}}+\frac{2}{3}z+\frac{42}{3}=0\Leftrightarrow 3{{z}^{2}}+2z+42=0\) Chọn B Câu hỏi 3 : Nghiệm phức có phần ảo dương của phương trình \({{z}^{2}}-z+4=0\) là
Đáp án: C Phương pháp giải: Phương trình \(a{{z}^{2}}+bz+c=0\) có hai nghiệm phân biệt \({{z}_{1}}=\frac{-\,b+\delta }{2a};\,\,{{z}_{2}}=\frac{-\,b-\delta }{2a}\) với \(\delta \) là căn bậc hai của biệt thức \(\Delta ={{b}^{2}}-4ac.\) Lời giải chi tiết: Ta có \({{z}^{2}}-z+4=0\Leftrightarrow {{z}^{2}}-2.z.\frac{1}{2}+\frac{1}{4}=-\,\frac{15}{4}\Leftrightarrow {{\left( z-\frac{1}{2} \right)}^{2}}={{\left( \frac{i\sqrt{15}}{2} \right)}^{2}}\Rightarrow \left[ \begin{align} z=\frac{1}{2}+\frac{\sqrt{15}}{2}i \\ z=\frac{1}{2}-\frac{\sqrt{15}}{2}i \\ \end{align} \right..\) Vậy số nghiệm phức có phần ảo dương là \(z=\frac{1}{2}+\frac{\sqrt{15}}{2}i.\) Chọn C Câu hỏi 4 : Gọi \({{z}_{1}},\,\,{{z}_{2}}\) là hai nghiệm phức của phương trình \({{z}^{2}}+2z+10=0.\) Tính giá trị của biểu thức \(A={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}.\)
Đáp án: C Phương pháp giải: Giải phương trình phức bậc hai và tính môđun của từng số phức. Lời giải chi tiết: Ta có \({{z}^{2}}+2z+10=0\Leftrightarrow {{\left( z+1 \right)}^{2}}=-\,9\Leftrightarrow {{\left( z+1 \right)}^{2}}={{\left( 3i \right)}^{2}}\Leftrightarrow \left[ \begin{align} & z=-\,1+3i \\ & z=-\,1-3i \\\end{align} \right..\) Khi đó \(A={{\left| {{z}_{1}} \right|}^{2}}+{{\left| {{z}_{2}} \right|}^{2}}={{\left| -\,1+3i \right|}^{2}}+{{\left| -\,1-3i \right|}^{2}}=10+10=20.\) Chọn C. Câu hỏi 5 : Kí hiệu \({{z}_{1}},{{z}_{2}}\) là hai nghiệm phức của phương trình \({{z}^{2}}+z+1=0\). Giá trị của biểu thức \(P=z_{1}^{2}+z_{2}^{2}+{{z}_{1}}{{z}_{2}}\) bằng:
Đáp án: C Phương pháp giải: Sử dụng định lí Vi-et. Lời giải chi tiết: \({{z}_{1}},{{z}_{2}}\) là hai nghiệm phức của phương trình \({{z}^{2}}+z+1=0\) nên theo định lí Vi-et ta có: \(\left\{ \begin{align} & {{z}_{1}}+{{z}_{2}}=-\frac{b}{a}=-1 \\ & {{z}_{1}}{{z}_{2}}=\frac{c}{a}=1 \\ \end{align} \right.\) \(P=z_{1}^{2}+z_{2}^{2}+{{z}_{1}}{{z}_{2}}={{\left( {{z}_{1}}+{{z}_{2}} \right)}^{2}}-{{z}_{1}}{{z}_{2}}={{\left( -1 \right)}^{2}}-1=0\) Chọn C Câu hỏi 6 : Tìm phần thực của số phức \(z_{1}^{2}+z_{2}^{2},\) biết rằng \({{z}_{1}},\,\,{{z}_{2}}\) là hai nghiệm phức của phương trình \({{z}^{2}}-4z+5=0.\)
Đáp án: B Phương pháp giải: Áp dụng định lí Vi-et của phương trình bậc hai. Lời giải chi tiết: Ta có \({{z}^{2}}-4z+5=0\Rightarrow \,\,\left\{ \begin{align} {{z}_{1}}+{{z}_{2}}=4 \\ {{z}_{1}}{{z}_{2}}=5 \\\end{align} \right.\Rightarrow \,\,z_{1}^{2}+z_{2}^{2}={{\left( {{z}_{1}}+{{z}_{2}} \right)}^{2}}2{{z}_{1}}{{z}_{2}}={{4}^{2}}-2.5=6.\) Chọn B. Câu hỏi 7 : Nghiệm phức có phần ảo dương của phương trình \({{z}^{2}}-z+1=0\) là \(z=a+bi,\,\,a,b\in R\). Tính \(a+\sqrt{3}b\)
Đáp án: A Phương pháp giải: Tìm nghiệm phức có phần ảo dương của phương trình \({{z}^{2}}-z+1=0\) bằng MTCT. Lời giải chi tiết: Sử dụng MTCT ta tính được nghiệm phức có phần ảo dương của phương trình trên là \(z=\frac{1}{2}+\frac{\sqrt{3}}{2}i\Rightarrow \left\{ \begin{align} a=\frac{1}{2} \\ b=\frac{\sqrt{3}}{2} \\ \end{align} \right.\Rightarrow a+\sqrt{3}b=\frac{1}{2}+\frac{3}{2}=2\) Chọn A. Câu hỏi 8 : Gọi \({{z}_{1}},\,\,{{z}_{2}}\) là hai nghiệm phức của phương trình \({{z}^{2}}+6z+13=0\) trong đó \({{z}_{1}}\) là số phức có phần ảo âm. Tìm số phức \(\omega ={{z}_{1}}+2{{z}_{2}}.\)
Đáp án: B Phương pháp giải: Giải phương trình bậc hai tìm nghiệm phức Lời giải chi tiết: Ta có \({{z}^{2}}+6z+13=0\Leftrightarrow {{z}^{2}}+6z+9=-4\Leftrightarrow {{\left( z+3 \right)}^{2}}={{\left( 2i \right)}^{2}}\Leftrightarrow \left[ \begin{align} & {{z}_{1}}=-\,3-2i \\ & {{z}_{2}}=-\,3+2i \\ \end{align} \right..\) Vậy \(\omega ={{z}_{1}}+2{{z}_{2}}=-2-2i+2\left( -3+2i \right)=-\,9+2i.\) Chọn B Câu hỏi 9 : Cho \({{z}_{1}}\) và \({{z}_{2}}\) là hai nghiệm phức của phương trình \(2{{z}^{2}}+6z+5=0\), trong đó \({{z}_{2}}\) có phần ảo âm. Phần thực và phần ảo của số phức \({{z}_{1}}+3{{z}_{2}}\) lần lượt là
Đáp án: C Phương pháp giải: Bấm máy tính để giải phương trình phức hệ số thực Lời giải chi tiết: Ta có \(2{{z}^{2}}+6z+5=0\,\,\Leftrightarrow \left[ \begin{align} & {{z}_{1}}=-\frac{3}{2}+\frac{1}{2}i \\ & {{z}_{2}}=-\frac{3}{2}-\frac{1}{2}i \\ \end{align} \right.\). Vậy \({{z}_{1}}+3{{z}_{2}}=-\frac{3}{2}+\frac{1}{2}i+3\left( -\frac{3}{2}-\frac{1}{2}i \right)=-\,6-i.\) Chọn C Câu hỏi 10 : Cho các số phức \({{z}_{1}}=3+2i,\,\,{{z}_{2}}=3-2i.\) Phương trình bậc hai có hai nghiệm \({{z}_{1}}\) và \({z_2}\) là
Đáp án: C Phương pháp giải: Tính tổng và tích hai nghiệm, áp dụng Viet đảo để tìm phương trình bậc hai Lời giải chi tiết: Ta có \(\left\{ \begin{align} & {{z}_{1}}+{{z}_{2}}=3+2i+3-2i=6 \\ & {{z}_{1}}{{z}_{2}}=\left( 3+2i \right)\left( 3-2i \right)=9+4=13 \\\end{align} \right.\Rightarrow \,\,{{z}_{1}},\,\,{{z}_{2}}\) là nghiệm phương trình \({z^2} - 6z + 13 = 0.\) Chọn C Câu hỏi 11 : Cho hai số phức \({z_1} = 2 + 3i,\,\,{z_2} = 3 - 2i\). Tích \({z_1}.{z_2}\) bằng
Đáp án: C Phương pháp giải: Lời giải chi tiết: \({z_1} = 2 + 3i,\,\,{z_2} = 3 - 2i \Rightarrow {z_1}.{z_2} = \left( {2 + 3i} \right).\left( {3 - 2i} \right) = 6 - 4i + 9i - 6{i^2} = 6 - 4i + 9i + 6 = 12 + 5i\) Chọn: C Câu hỏi 12 : Giải phương trình \({z^2} - 4z + 5 = 0\) trên tập số phức ta được các nghiệm:
Đáp án: B Phương pháp giải: Sử dụng MTCT. Lời giải chi tiết: Sử dụng MTCT ta tính được : Chọn B. Câu hỏi 13 : Phương trình bậc hai nào dưới đây nhận hai số phức \(2 + 3i\) và \(2 - 3i\) làm nghiệm?
Đáp án: C Phương pháp giải: Sử dụng định lý: Nếu \(\left\{ \begin{array}{l}{z_1} + {z_2} = S\\{z_1}{z_2} = P\end{array} \right.\) thì \({z_1},{z_2}\) là nghiệm của phương trình \({z^2} - Sz + P = 0\). Lời giải chi tiết: Ta có \(\left\{ \begin{array}{l}\left( {2 - 3i} \right)\left( {2 + 3i} \right) = 13\\\left( {2 - 3i} \right) + \left( {2 + 3i} \right) = 4\end{array} \right.\). Vậy hai số phức \(2 + 3i\) và \(2 - 3i\) là nghiệm của phương trình \({z^2} - 4z + 13 = 0\). Chọn C. Câu hỏi 14 : Cho số phức z = 1 + 2i. Tìm tổng phần thực và phần ảo của số phức \(w = 2z + \overline z \).
Đáp án: B Phương pháp giải: Sử dụng các công thức cộng trừ số phức, xác định số phức \(w\). Lời giải chi tiết: Ta có: \(\begin{array}{l}z = 1 + 2i \Rightarrow \overline z = 1 - 2i\\w = 2.z + \overline z = 2 + 4i + 1 - 2i = 3 + 2i \Rightarrow \left\{ \begin{array}{l}{\mathop{\rm Re}\nolimits} w = 3\\{\mathop{\rm Im}\nolimits} w = 2\end{array} \right.\end{array}\) Tổng phần thực và phần ảo của \(w = 2z + \overline z \) là: \(3 + 2 = 5\) Chọn B. Câu hỏi 15 : Cho số phức \(z = 1 - i\) . Biểu diễn số \({z^2}\) là điểm:
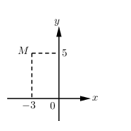
Đáp án: D Phương pháp giải: Điểm biểu diễn của số phức \(z = a + bi,\,\,\left( {a,b \in \mathbb{R}} \right)\) là điểm \(M\left( {a;b} \right)\). Lời giải chi tiết: \(z = 1 - i \Rightarrow {z^2} = {\left( {1 - i} \right)^2} = - 2i\), có điểm biểu diễn là: \(N\left( {0; - 2} \right)\). Chọn: D Câu hỏi 16 : Điểm \(M\) trong hình vẽ biểu diễn số phức \(z.\) Chọn kết luận đúng về số phức \(\overline z .\)
Đáp án: D Phương pháp giải: Cho số phức \(z = x + yi\;\;\left( {x,\;y \in \mathbb{R}} \right) \Rightarrow M\left( {x;\;y} \right)\) là điểm biểu diễn số phức \(z.\) Cho số phức \(z = a + bi \Rightarrow \overline z = a - bi.\) Lời giải chi tiết: Ta thấy \(M\left( { - 3;\,5} \right)\) biểu diễn số phức \(z \Rightarrow z = - 3 + 5i \Rightarrow \overline z = - 3 - 5i.\) Chọn D. Câu hỏi 17 : Phương trình nào dưới đây nhận được hai số phức \( - \sqrt 3 i\) và \(\sqrt 3 i\) là nghiệm?
Đáp án: B Phương pháp giải: Phương trình nhận được hai số phức \({z_1}\) và \({z_2}\) là nghiệm là \(\left( {z - {z_1}} \right)\left( {z - {z_2}} \right) = 0\). Lời giải chi tiết: Phương trình \(\left( {z - \sqrt 3 i} \right)\left( {z + \sqrt 3 i} \right) = 0 \Leftrightarrow {z^2} + 3 = 0\) nhận được hai số phức \( - \sqrt 3 i\) và \(\sqrt 3 i\) là nghiệm. Chọn: B Câu hỏi 18 : Tập nghiệm của phương trình \({x^2} + 9 = 0\) trên tập số phức là:
Đáp án: D Phương pháp giải: Lời giải chi tiết: Ta có: \({x^2} + 9 = 0 \Leftrightarrow {x^2} = - 9 \Leftrightarrow x = \pm 3i\) Tập nghiệm của phương trình \({x^2} + 9 = 0\) trên tập số phức là: \(\left\{ { - 3i;3i} \right\}\). Chọn: D Câu hỏi 19 : Tìm số phức \(z\) có phần ảo dương thỏa mãn \({z^2} - 2z + 10 = 0\).
Đáp án: A Phương pháp giải: Sử dụng MTCT giải phương trình và kết luận. Lời giải chi tiết: \({z^2} - 2z + 10 = 0 \Rightarrow \left[ \begin{array}{l}z = 1 + 3i\\z = 1 - 3i\end{array} \right.\) Vậy số phức \(z\) có phần ảo dương thỏa mãn \({z^2} - 2z + 10 = 0\) là \(z = 1 + 3i\). Chọn A Câu hỏi 20 : Gọi \({z_1}\)và \({z_2}\) là hai nghiệm phức của phương trình \(2{z^2} - 3z + 12 = 0\). Khi đó \({z_1} + {z_2}\) bằng
Đáp án: A Phương pháp giải: Sử dụng định lí Vi-ét. Lời giải chi tiết: Áp dụng định lí Vi-ét ta có: \({z_1} + {z_2} = \dfrac{3}{2}\). Chọn A. Câu hỏi 21 : Phương trình \(a{x^2} + bx + c = 0\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai nghiệm phức phân biệt khi và chỉ khi:
Đáp án: C Phương pháp giải: Phương trình \(a{x^2} + bx + c = 0\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có hai nghiệm phức phân biệt khi và chỉ khi: \(\left\{ \begin{array}{l}a \ne 0\\{b^2} - 4ac < 0\end{array} \right.\) Chọn C Lời giải chi tiết: Câu hỏi 22 : Xét phương trình bậc hai \(a{z^2} + bz + c = 0\) trên tập \(\mathbb{C}\,\,\left( {a \ne 0,\,\,a,b,c \in \mathbb{R}} \right)\). Tìm điều kiện cần và đủ để phương trình có hai nghiệm \({z_1}\) và \({z_2}\) là hai số phức liên hợp với nhau.
Đáp án: D Phương pháp giải: Biện luận số nghiệm của phương trình bậc hai. Lời giải chi tiết: Điều kiện cần và đủ để phương trình có hai nghiệm \({z_1}\) và \({z_2}\) là hai số phức liên hợp với nhau là \({b^2} - 4ac \le 0\). Chọn: D Câu hỏi 23 : Kí hiệu \({z_1},\,\,{z_2}\) là hai nghiệm phức của phương trình \({z^2} - 3z + 3 = 0\). Giá trị của \({\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2}\) bằng:
Đáp án: C Phương pháp giải: +) Giải phương trình tìm \({z_1},\,\,{z_2}\). +) \(z = a + bi \Rightarrow \left| z \right| = \sqrt {{a^2} + {b^2}} \). Lời giải chi tiết: \({z^2} - 3z + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = \dfrac{3}{2} + \dfrac{{\sqrt 3 }}{2}i\\{z_2} = \dfrac{3}{2} - \dfrac{{\sqrt 3 }}{2}i\end{array} \right. \Rightarrow \left| {{z_1}^2} \right| = {\left| {{z_2}} \right|^2} = 3\). Vậy \({\left| {{z_1}} \right|^2} + {\left| {{z_2}} \right|^2} = 6\) Chọn C Câu hỏi 24 : Biết phương trình \({z^2} + az + b = 0,\,\,\left( {a,b \in \mathbb{R}} \right)\) có một nghiệm là \(4 + 5i\), tìm nghiệm còn lại.
Đáp án: D Phương pháp giải: Phương trình bậc hai có nghiệm phức thì có 2 nghiệm phức là liên hợp của nhau. Lời giải chi tiết: Phương trình \({z^2} + az + b = 0,\,\,\left( {a,b \in \mathbb{R}} \right)\) có một nghiệm là \(4 + 5i \Rightarrow \) Nghiệm còn lại là \(4 - 5i\). Chọn: D Câu hỏi 25 : Kí hiệu \({z_1},\,{z_2}\) là hai nghiệm phức của phương trình \({z^2} - 6z + 25 = 0\). Giá trị của \(\left| {{z_1}} \right| + \left| {{z_2}} \right| + {z_1}.{z_2}\) bằng
Đáp án: D Phương pháp giải: Giải phương trình tìm \({z_1},\,\,{z_2}\). Lời giải chi tiết: \(\begin{array}{l}{z^2} - 6z + 25 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = 3 + 4i\\{z_2} = 3 - 4i\end{array} \right. \Rightarrow \left| {{z_1}} \right| = \left| {{z_2}} \right| = 5\\ \Rightarrow \left| {{z_1}} \right| + \left| {{z_2}} \right| + {z_1}.{z_2} = 5 + 5 + \left( {3 + 4i} \right)\left( {3 - 4i} \right) = 10 + 25 = 35\end{array}\) Chọn D. Câu hỏi 26 : Giải phương trình \({z^2} - 2z + 3 = 0\) trên tậ số phức ta được các nghiệm:
Đáp án: D Phương pháp giải: Sử dụng máy tính bấm nghiệm của phương trình. Lời giải chi tiết: \({z^2} - 2z + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = 1 + \sqrt 2 i\\{z_2} = 1 - \sqrt 2 i\end{array} \right..\)
Chọn D. Câu hỏi 27 : Gọi các số phức \({z_1};\,\,{z_2}\) là các nghiệm của phương trình \(3{z^2} - 2z + 12 = 0\). Giá trị biểu thức \(M = 2\left| {{z_1}} \right| - 3\left| {{z_2}} \right|\) bằng
Đáp án: C Phương pháp giải: - Giải phương trình bậc hai tìm hai nghiệm \({z_1},\,\,{z_2}\). - Số phức \(z = a + bi\) có môđun \(\left| z \right| = \sqrt {{a^2} + {b^2}} \). Tính \(\left| {{z_1}} \right|,\,\,\left| {{z_2}} \right|\). - Thay vào tính giá trị biểu thức \(M\). Lời giải chi tiết: Phương trình \(3{z^2} - 2z + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}{z_1} = \dfrac{1}{3} + \dfrac{{\sqrt {35} }}{3}i\\{z_2} = \dfrac{1}{3} - \dfrac{{\sqrt {35} }}{3}i\end{array} \right.\)\( \Rightarrow \left| {{z_1}} \right| = \left| {{z_2}} \right| = 2\). Vậy \(M = 2\left| {{z_1}} \right| - 3\left| {{z_2}} \right| = 2.2 - 3.2 = - 2.\) Chọn C. Câu hỏi 28 : Nghiệm phức có phần ảo dương của phương trình \({z^2} - 2z + 5 = 0\) là:
Đáp án: D Phương pháp giải: Tìm hai nghiệm phức của phương trình, sử dụng MTCT. Lời giải chi tiết: Phương trình \({z^2} - 2z + 5 = 0 \Leftrightarrow \left[ \begin{array}{l}z = 1 + 2i\\z = 1 - 2i\end{array} \right.\) Vậy nghiệm phức có phần ảo dương là \(z = 1 + 2i.\) Chọn D. Câu hỏi 29 : Hai nghiệm của phương trình \({z^2} + 4z + 13 = 0\) trên tập số phức là
Đáp án: B Phương pháp giải: Sử dụng máy tính để tìm nghiệm của phương trình. Lời giải chi tiết: \({z^2} + 4z + 13 = 0 \Leftrightarrow \left\{ \begin{array}{l}{z_1} = - 2 - 3i\\{z_2} = - 2 + 3i\end{array} \right.\). Chọn B. Câu hỏi 30 : Trong không gian Oxyz, khoảng cách từ điểm \(M\left( {2; - 3;0} \right)\) đến mặt phẳng \(\left( P \right):\,\,x + 5y - 2z + 1 = 0\) bằng
Đáp án: A Phương pháp giải: Khoảng cách từ \(M\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):\,\,Ax + By + Cz + D = 0\) là \(d\left( {M;\left( P \right)} \right) = \dfrac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\). Lời giải chi tiết: \(d\left( {M;\left( P \right)} \right) = \dfrac{{\left| {2 + 5\left( { - 3} \right) - 2.0 + 1} \right|}}{{\sqrt {1 + {5^2} + {{\left( { - 2} \right)}^2}} }} = \dfrac{{2\sqrt {30} }}{5}.\) Chọn A.
|