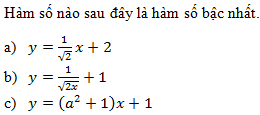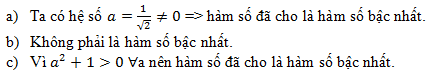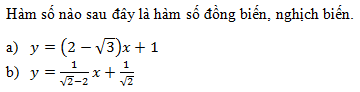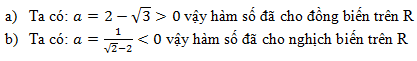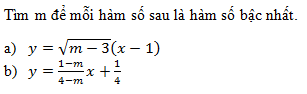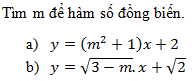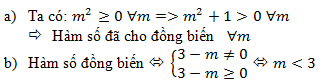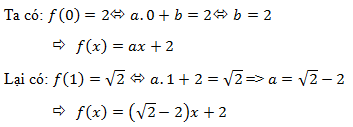25 bài tập cơ bản về Hàm số bậc nhất

Câu hỏi 1 :

Tìm điều kiện xác định của hàm số sau:

Câu 1: $y = \sqrt {{x^2} - 2x - 3}$

$\left[ \begin{array}{l} x \ge 3\\ x \le - 1 \end{array} \right.$
$- 1 \le x \le 3$
$- 1 < x < 3$
$\left[ \begin{array}{l} x > 3\\ x < - 1 \end{array} \right.$

Đáp án: A

Phương pháp giải:

Hàm số $y = \sqrt {f\left( x \right)}$ có điều kiện là $f\left( x \right) \ge 0$

Hàm số $y = \sqrt {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}}$ có điều kiện là $\left\{ \begin{array}{l}\dfrac{{f\left( x \right)}}{{g\left( x \right)}} \ge 0\\g\left( x \right) \ne 0\end{array} \right.$

Lời giải chi tiết:

Điều kiện ${x^2} - 2x - 3 \ge 0 \Leftrightarrow \left( {x + 1} \right)\left( {x - 3} \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 3\\x \le - 1\end{array} \right.$

Đáp án - Lời giải

Câu 2: $y = \sqrt {\dfrac{{x - 1}}{{2 - x}}}$

$1 \le x \le 2$
$\left[ \begin{array}{l} x > 2\\ x \le 1 \end{array} \right.$
$1 \le x < 2$
$\left[ \begin{array}{l} x \ge 2\\ x \le 1 \end{array} \right.$

Đáp án: C

Phương pháp giải:

Hàm số $y = \sqrt {f\left( x \right)}$ có điều kiện là $f\left( x \right) \ge 0$

Hàm số $y = \sqrt {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}}$ có điều kiện là $\left\{ \begin{array}{l}\dfrac{{f\left( x \right)}}{{g\left( x \right)}} \ge 0\\g\left( x \right) \ne 0\end{array} \right.$

Lời giải chi tiết:

Điều kiện $\left\{ \begin{array}{l}\dfrac{{x - 1}}{{2 - x}} \ge 0\\x \ne 2\end{array} \right. \Leftrightarrow 1 \le x < 2$

Đáp án - Lời giải

Câu 3: $y = 2 - x$

$x \in \backslash \left\{ 0 \right\}$
$x \in \mathbb{R}$ .
$x \ge 0$
$x<0$

Đáp án: B

Phương pháp giải:

Hàm số $y = \sqrt {f\left( x \right)}$ có điều kiện là $f\left( x \right) \ge 0$

Hàm số $y = \sqrt {\dfrac{{f\left( x \right)}}{{g\left( x \right)}}}$ có điều kiện là $\left\{ \begin{array}{l}\dfrac{{f\left( x \right)}}{{g\left( x \right)}} \ge 0\\g\left( x \right) \ne 0\end{array} \right.$

Lời giải chi tiết:

Điều kiện $x \in \mathbb{R}$ .

Đáp án - Lời giải

Câu hỏi 2 :

Cho hàm số $f\left( x \right) = \sqrt {x + 2\sqrt x + 1}$

Câu 1: Tìm tập xác định của hàm số

$x > 0$
$x \ge 0$
$x \ge 0,\,\,x \ne 1$
$x \ge 0,\,\,x \ne \pm 1$

Đáp án: B

Phương pháp giải:

Hàm số $y = \sqrt {f\left( x \right)}$ có điều kiện là $f\left( x \right) \ge 0$

Lời giải chi tiết:

ĐKXĐ: $\left\{ \begin{array}{l}x + 2\sqrt x + 1 \ge 0\\x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {\sqrt x + 1} \right)^2} \ge 0\,\,\left( {luon\,\,dung} \right)\\x \ge 0\end{array} \right. \Rightarrow x \ge 0$

Đáp án - Lời giải

Câu 2: Tính $f\left( {3 + 2\sqrt 2 } \right)$ .

$f\left( {3 + 2\sqrt 2 } \right) = 2\sqrt 2 + 2$
$f\left( {3 + 2\sqrt 2 } \right) = 2\sqrt 2 + 3$
$f\left( {3 + 2\sqrt 2 } \right) = \sqrt 2 + 1$
$f\left( {3 + 2\sqrt 2 } \right) = \sqrt 2 + 2$

Đáp án: D

Phương pháp giải:

+) Rút gọn hàm $f\left( x \right) = \sqrt {x + 2\sqrt x + 1}$ .

+) Thay $x = 3 + 2\sqrt 2$ .

Lời giải chi tiết:

Với $x \ge 0$ ta có : $f\left( x \right) = \sqrt {x + 2\sqrt x + 1} = \sqrt {{{\left( {\sqrt x + 1} \right)}^2}} = \left| {\sqrt x + 1} \right| = \sqrt x + 1\,\,\left( {Do\,\,\sqrt x + 1 > 0\,\,\forall x \ge 0} \right)$

Ta có : $x = 3 + 2\sqrt 2 = {\left( {\sqrt 2 + 1} \right)^2} \Rightarrow \sqrt x = \sqrt {{{\left( {\sqrt 2 + 1} \right)}^2}} = \sqrt 2 + 1$
Suy ra : $f\left( {3 + 2\sqrt 2 } \right) = \left( {\sqrt 2 + 1} \right) + 1 = \sqrt 2 + 2$

Đáp án - Lời giải

Câu hỏi 3 :

A Hàm số a) và b).
B Hàm số a) và c).
C Hàm số b) và c).
D Hàm số a), b) và c).

Đáp án: B

Phương pháp giải:

Lời giải chi tiết:

Vậy hàm số a) và c) là hàm số bậc nhất

Đáp án - Lời giải

Câu hỏi 4 :

A a) là hàm số nghịch biến.

b) là hàm số nghịch biến.
B a) là hàm số đồng biến.

b) là hàm số đồng biến.
C a) là hàm số đồng biến.

b) là hàm số nghịch biến.
D a) là hàm số nghịch biến.

b) là hàm số đồng biến.

Đáp án: C

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 5 :

Trong các hàm số dưới đây, hàm số nào là hàm số bậc nhất?

$y = \frac{1}{x} + 2$
$y = {x^2}$
$y = - 2x + 1$
$y = 2{x^2} + 1$

Đáp án: C

Phương pháp giải:

Hàm số bậc nhất có dạng $y = ax + b\,\,\,\left( {a \ne 0} \right)$

Lời giải chi tiết:

Trong các hàm số ở các đáp án, chỉ có đáp án C có hàm số là hàm số bậc nhất một ẩn.

Chọn C.

Đáp án - Lời giải

Câu hỏi 6 :

Hàm số $y = ax + 1$ đồng biến trên $\mathbb{R}$ khi và chỉ khi

$a \le 0$
$a < 0$
$a \ge 0$
$a > 0$

Đáp án: D

Phương pháp giải:

Hàm số bậc nhất $y = ax + b\,\,\left( {a \ne 0} \right)$ đồng biến trên $\mathbb{R} \Leftrightarrow a > 0.$

Lời giải chi tiết:

Hàm số $y = ax + 1$ đồng biến trên $\mathbb{R} \Leftrightarrow a > 0.$

Chọn D.

Đáp án - Lời giải

Câu hỏi 7 :

Hệ số góc của đường thẳng $y = - 2x - 1$ là:

$- 2$
$- 1$
$1$
$2$ .

Đáp án: A

Phương pháp giải:

Phương trình đường thẳng có dạng $y = kx + b$ có hệ số góc là $k.$

Lời giải chi tiết:

Phương trình đường thẳng $y = - 2x - 1$ có hệ số góc là $- 2$

Chọn A

Đáp án - Lời giải

Câu hỏi 8 :

Hàm số nào sau đây là hàm số bậc nhất?

$y = 2{x^2}$
$y = \sqrt x + 1$
$y = 1 - 2x$
$y = - \frac{1}{x}$

Đáp án: C

Phương pháp giải:

Hàm số $y = ax + b\,\,$ là hàm số bậc nhất $\Leftrightarrow a \ne 0.$

Lời giải chi tiết:

Trong các đáp án đã cho, chỉ có đáp án C có hàm số là hàm số bậc nhất.

Chọn C.

Đáp án - Lời giải

Câu hỏi 9 :

Đường thẳng $y = 4x - 5$ có hệ số góc bằng

$5$
$- 5$
$- 4$
$4$

Đáp án: D

Phương pháp giải:

Đường thẳng $y = ax + b\,\,\,\left( {a \ne 0} \right)$ có hệ số góc là $a.$

Lời giải chi tiết:

Đường thẳng $y = 4x - 5$ có hệ số góc là $a = 4.$

Chọn D.

Đáp án - Lời giải

Câu hỏi 10 :

Hàm số nào dưới đây là hàm số đồng biến trên $\mathbb{R}?$

$y = - \frac{1}{2}x$
$y = - 2x$
$y = 2x + 1$
$y = - 3x + 1$

Đáp án: C

Phương pháp giải:

Hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ đồng biến trên $\mathbb{R}$ khi $a > 0$ và nghịch biến trên $\mathbb{R}$ khi $a < 0.$

Lời giải chi tiết:

Trong các đáp án, chỉ có đáp án C có hàm số $y = 2x + 1$ có $a = 2 > 0$ nên hàm số đồng biến trên $\mathbb{R}.$

Chọn C.

Đáp án - Lời giải

Câu hỏi 11 :

Trong các hàm số sau, hàm số nào là hàm số bậc nhất?

$y = - 4x + 3.$
$y = 2 + \dfrac{1}{x}.$
$y = \sqrt x + 3.$
$y = 2{x^2}.$

Đáp án: A

Phương pháp giải:

Hàm số bậc nhất là hàm số có dạng $y = ax + b\,\,\left( {a \ne 0} \right)$ .

Lời giải chi tiết:

Hàm số $y = - 4x + 3$ là hàm số bậc nhất.

Chọn A.

Đáp án - Lời giải

Câu hỏi 12 :

Tìm $m$ để hàm số $y = \left( {m + 2} \right)x - 5$ đồng biến trên $\mathbb{R}$ .

$m > - 2.$
$m = - 2.$
$m \ne - 2.$
$m < - 2.$

Đáp án: A

Phương pháp giải:

Cho hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ :

- Hàm số đồng biến trên $\mathbb{R}$ khi $a > 0$ .

- Hàm số đồng biến trên $\mathbb{R}$ khi $a < 0$ .

Lời giải chi tiết:

Hàm số $y = \left( {m + 2} \right)x - 5$ đồng biến trên $\mathbb{R}$ khi và chỉ khi $m + 2 > 0 \Leftrightarrow m > - 2$ .

Chọn A.

Đáp án - Lời giải

Câu hỏi 13 :

Trong các hàm số sau, hàm số nào nghịch biến trên $\mathbb{R}$ ?

$y = 2x - 7.$
$y = - 3x + 5.$
$y = - 2{x^2}.$
$y = 5{x^2}.$

Đáp án: B

Phương pháp giải:

Hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ nghịch biến trên $\mathbb{R}$ khi $a < 0.$

Lời giải chi tiết:

Trong các đáp án, chỉ có hàm số $y = - 3x + 5$ là hàm số nghịch biến trên $\mathbb{R}.$

Chọn B.

Đáp án - Lời giải

Câu hỏi 14 :

Trong các hàm số sau, hàm số nào đồng biến trên $R$ ?

$y = 1 - x$
$y = 2x - 3$
$y = \left( {1 - \sqrt 2 } \right)x$
$y = - 2x + 6$

Đáp án: B

Phương pháp giải:

Hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ đồng biến trên $\mathbb{R}$ khi $a > 0$ , nghịch biến trên $\mathbb{R}$ khi $a < 0.$

Lời giải chi tiết:

Trong các hàm số đã cho hàm số $y = 2x - 3$ đồng biến trên $\mathbb{R}.$

Chọn B.

Đáp án - Lời giải

Câu hỏi 15 :

Trong các hàm số sau, hàm số nào là đồng biến trên $\mathbb{R}?$

$y = - x + 5$
$y = 2x + 1$
$y = 2019 - 2x$
$y = 2020$

Đáp án: B

Phương pháp giải:

Hàm số $y = ax + b\,\,\,\left( {a \ne 0} \right)$ đồng biến trên $\mathbb{R} \Leftrightarrow a > 0.$

Lời giải chi tiết:

Trong các hàm số ở các đáp án chỉ có đáp án B là hàm số có hệ số góc $a = 2 > 0 \Rightarrow y = 2x + 1$ là hàm số đồng biến trên $\mathbb{R}.$

Chọn B.

Đáp án - Lời giải

Câu hỏi 16 :

$\begin{array}{l} a)\,\,m > 3\\ b)\,\,m \ne 4 \end{array}$
$\begin{array}{l} a)\,\,m > 3\\ b)\,\,m \ne 1 \end{array}$
$\begin{array}{l} a)\,\,m \ge 3\\ b)\,\,\left\{ \begin{array}{l} m \ne 1\\ m \ne 4 \end{array} \right. \end{array}$
$\begin{array}{l} a)\,\,m > 3\\ b)\,\,\left\{ \begin{array}{l} m \ne 1\\ m \ne 4 \end{array} \right. \end{array}$

Đáp án: D

Phương pháp giải:

Lời giải chi tiết:

$\eqalign{& a)\,\,DK:\left\{ \matrix{m - 3 \ge 0 \hfill \cr m - 3 \ne 0 \hfill \cr} \right. \Leftrightarrow m > 3 \cr & b)\,\,DK:\left\{ \matrix{{{1 - m} \over {4 - m}} \ne 0 \hfill \cr 4 - m \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{1 - m \ne 0 \hfill \cr 4 - m \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{m \ne 1 \hfill \cr m \ne 4 \hfill \cr} \right. \cr}$

Đáp án - Lời giải

Câu hỏi 17 :

$\begin{array}{l} a)\,\,\forall m\\ b)\,\,m < 3 \end{array}$
$\begin{array}{l} a)\,\,m \ne - 1\\ b)\,\,m < 3 \end{array}$
$\begin{array}{l} a)\,\,m \ne 1\\ b)\,\,m > 3 \end{array}$
$\begin{array}{l} a)\,\,m \ne - 1\\ b)\,\,m > 3 \end{array}$

Đáp án: A

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 18 :

$\begin{array}{l} a = \sqrt 2 - 2\\ b = -2 \end{array}$
$\begin{array}{l} a = \sqrt 2 - 2\\ b = 2 \end{array}$
$\begin{array}{l} a = \sqrt 2 + 2\\ b = 2 \end{array}$
$\begin{array}{l} a = \sqrt 2 + 2\\ b =- 2 \end{array}$

Đáp án: B

Phương pháp giải:

Lời giải chi tiết:

Đáp án - Lời giải

Câu hỏi 19 :

Điều kiện để hàm số bậc nhất $y = \left( {1 - m} \right)x + m\,\,\left( {m \ne 1} \right)$ là hàm số nghịch biến là:

$m > 1$
$m \ge 1$
$m \le 1$
$m < 1$

Đáp án: A

Phương pháp giải:

Hàm số $y = ax + b$ nghịch biến $\Leftrightarrow a < 0.$

Lời giải chi tiết:

Hàm số nghịch biến $\Leftrightarrow 1 - m < 0 \Leftrightarrow m > 1.$

Chọn A.

Đáp án - Lời giải

Câu hỏi 20 :

Với giá trị nào của a thì hàm số $y = \left( {a - 5} \right)x + 1$ đồng biến trên tập $\mathbb{R}$ ?

$a < 5$
$a > 5$
$a = 5$
$a > - 5$

Đáp án: B

Phương pháp giải:

Hàm số $y = ax + b$ đồng biến $\Leftrightarrow a > 0.$

Lời giải chi tiết:

Hàm số đồng biến $\Leftrightarrow a - 5 > 0 \Leftrightarrow a > 5.$

Chọn B.

Đáp án - Lời giải

Câu hỏi 21 :

Hàm số $y = (m - 2017)x + 2018$ đồng biến khi

$m \ne 2017$
$m \ge 2017$
$m > 2017$
$m < 2017$

Đáp án: C

Phương pháp giải:

Hàm số $y = ax + b\,\,$ đồng biến khi $a > 0$ .

Lời giải chi tiết:

Hàm số $y = (m - 2017)x + 2018$ đồng biến khi $m - 2017 > 0\,\, \Leftrightarrow \,\,m > 2017$ .

Chọn C.

Đáp án - Lời giải

Câu hỏi 22 :

Tìm tất cả các giá trị của $m$ để hàm số bậc nhất $y = \left( {2019 - m} \right)x + 2020$ nghịch biến trên $\mathbb{R}.$

$m > - 2019$
$m > 2019$
$m < 2019$
$m < - 2019$

Đáp án: B

Phương pháp giải:

Hàm số $y = ax + b\,\,\,\left( {a \ne 0} \right)$ nghịch biến trên $\mathbb{R} \Leftrightarrow a < 0.$

Lời giải chi tiết:

Hàm số bậc nhất $y = \left( {2019 - m} \right)x + 2020$ nghịch biến trên $\mathbb{R}$

$\Leftrightarrow 2019 - m < 0 \Leftrightarrow m > 2019.$

Chọn B.

Đáp án - Lời giải

Câu hỏi 23 :

Tìm $m$ để hàm số $y = \left( {1 - 2m} \right)x + 3$ là hàm số đồng biến?

$m < \frac{1}{2}$
$m > \frac{1}{2}$
$m \le \frac{1}{2}$
$m \ge \frac{1}{2}$

Đáp án: A

Phương pháp giải:

Hàm số $y = ax + b\,\,\,\left( {a \ne 0} \right)$ đồng biến $\Leftrightarrow a > 0$ , nghịch biến $\Leftrightarrow a < 0.$

Lời giải chi tiết:

Hàm số $y = \left( {1 - 2m} \right)x + 3$ đồng biến $\Leftrightarrow 1 - 2m > 0 \Rightarrow m < \frac{1}{2}.$

Chọn A

Đáp án - Lời giải

Câu hỏi 24 :

Tìm tất cả các giá trị của $m$ để hàm số $y = \left( {1 - m} \right)x + m + 1$ đồng biến trên $\mathbb{R}.$

$m > 1$
$m < 1$
$m < - 1$
$m > - 1$

Đáp án: B

Phương pháp giải:

Hàm số $y = ax + b\,\,\left( {a \ne 0} \right)$ đồng biến trên $\mathbb{R}$ khi $a > 0$ và nghịch biến trên $\mathbb{R}$ khi $a < 0.$

Lời giải chi tiết:

Hàm số $y = \left( {1 - m} \right)x + m + 1$ đồng biến trên $\mathbb{R} \Leftrightarrow 1 - m > 0 \Leftrightarrow m < 1.$

Chọn B.

Đáp án - Lời giải

Câu hỏi 25 :

Điều kiện để hàm số $y = \left( { - m + 3} \right)x - 3$ đồng biến trên $\mathbb{R}$ là:

$m = 3$
$m < 3$
$m \ge 3$
$x \ne 3$

Đáp án: B

Phương pháp giải:

Hàm số $y = ax + b$ đồng biến trên $\mathbb{R} \Leftrightarrow a > 0.$

Lời giải chi tiết:

Hàm số $y = \left( { - m + 3} \right)x - 3$ đồng biến trên $\mathbb{R} \Leftrightarrow - m + 3 > 0 \Leftrightarrow m < 3.$

Chọn B.

Đáp án - Lời giải

25 bài tập cơ bản về Hàm số bậc nhất

15 bài tập vận dụng về Hàm số bậc nhất