15 bài tập vận dụng về Hàm số bậc nhấtLàm bàiCâu hỏi 1 : Điều kiện để hàm số y=(−m+3)x−3 đồng biến trên R là:
Đáp án: B Phương pháp giải: Hàm số y=ax+b đồng biến trên R⇔a>0. Lời giải chi tiết: Hàm số y=(−m+3)x−3 đồng biến trên R⇔−m+3>0⇔m<3. Chọn B. Câu hỏi 2 : Cho các điểm sau, điểm nào không thuộc đồ thị của hàm số y=−3x+1?
Đáp án: A Phương pháp giải: Thay tọa độ các điểm trong các đáp án vào công thức hàm số đã cho và chọn đáp án đúng. Lời giải chi tiết: +) Xét điểm M(1;−4) ta có: −3.1+1=−2≠−4⇒M∉d:y=−3x+1. Chọn A. Câu hỏi 3 :
Đáp án: A Phương pháp giải: Lời giải chi tiết:
Câu hỏi 4 : Tìm điểm mà hàm số y=(m−2)x+3m luôn đi qua trong mặt phẳng tọa độ Oxy.
Đáp án: D Phương pháp giải: Đưa hàm số ban đầu về dạng m.f(x;y)+g(x;y)=0. Điểm đồ thị luôn đi qua là nghiệm của hệ phương trình {f(x;y)=0g(x;y)=0 Lời giải chi tiết: y=(m−2)x+3m Giả sử đồ thị đi qua điểm C(x0;y0)cố định. Ta có y0=(m−2)x0+3m⇔m(x0+3)−(2x0+y0)=0 đúng ∀m {x0+3=02x0+y0=0⇔{x=−3y0=6 Vậy đồ thị hàm số luôn đi qua điểm (−3;6) Câu hỏi 5 : Hãy biểu diễn y theo x được cho dưới đây. Biểu thị nào là một hàm số bậc nhất : Câu 1: Chu vi y của hình vuông cạnh x.
Đáp án: A Phương pháp giải: Sử dụng các công thức tính chu vi: +) Chu vi hình vuông cạnh a là C=4a. Lời giải chi tiết: Câu 2: Chu vi y của đường tròn bán kính x.
Đáp án: A Phương pháp giải: Sử dụng các công thức tính chu vi: +) Chu vi đường tròn bán kính a là C=2πa. Lời giải chi tiết: Đường tròn có đường bán kinh bằng x thì chu vi là 2πx Suy ra y=2πx là hàm số bậc nhất. Câu hỏi 6 : Một xí nghiệp may cần thanh lý 1410 bộ quần áo. Biết mỗi ngày xí nghiệp đó bán được 30 bộ quần áo. Gọi x là số ngày đã bán, y là số bộ quần áo còn lại sau x ngày bán. Câu 1: Hãy lập công thức tính y theo x.
Đáp án: B Phương pháp giải: Tính số quần áo bán được sau x ngày bán từ đó suy ra y theo x. Lời giải chi tiết: Mỗi ngày xí nghiệp đó bán được 30 bộ quần áo nên sau x ngày bán xí nghiệp đó bán được 30x bộ quần áo. y là số bộ quần áo còn lại sau x ngày bán ⇒y=1410−30x (1) Chọn B. Câu 2: Xí nghiệp cần bao nhiêu ngày để bán hết số bộ quần áo cần thanh lý?
Đáp án: C Phương pháp giải: Bán hết thì y=0 thế vào công thức ở a) để tính số ngày x. Lời giải chi tiết: Để xí nghiệp bán hết số bộ quần áo cần thanh lý thì y=0 thế vào (1) ⇒1410−30x=0⇔30x=1410⇔x=47 (ngày) Vậy xí nghiệp cần 47 ngày để bán hết số bộ quần áo cần thanh lý. Chọn C. Câu hỏi 7 : Tại bề mặt đại dương, áp suất nước bằng áp suất khí quyển và là 1 atm (atmosphere). Bên dưới mặt nước, áp suất nước tăng thêm 1 atm cho mỗi 10 mét sâu xuống. Biết rằng mối liên hệ giữa áp suất y(atm) và độ sâu x(m) dưới mặt nước là một hàm số bậc nhất có dạng y=ax+b. Câu 1: Xác định các hệ số a và b Dựa vào giả thiết bài toán suy ra các giá trị x,y tương ứng, từ đó tìm a,b. b
Đáp án: C Phương pháp giải: Dựa vào giả thiết bài toán suy ra các giá trị x,y tương ứng, từ đó tìm a,b. Lời giải chi tiết: y=ax+b Tại bề mặt đại dương, áp suất nước là 1atm nên ta có: 1=a.0+b⇔b=1. Ở độ sâu 10m, áp suất nước tăng thêm 1atm nên ta có: 2=a.10+1⇔10a=1⇔a=110. Vậy a=110,b=1. Chọn C. Câu 2: Một người thợ lặn đang ở độ sâu bao nhiêu nếu người ấy chịu một áp suất là 2,85atm?
Đáp án: B Phương pháp giải: Thay y=2,85 vào hàm số đã tìm được ở ý a) để tìm x. Lời giải chi tiết: Ta có hàm số biểu thị mối liên hệ giữa áp suất và độ sau dưới mặt nước là: y=110x+1. Người thợ lặn chịu được áp suất 2,85atm nên ta có: 2,85=110.x+1⇔110x=1,85⇔x=18,5m. Vậy người thợ lặn ở độ sau 18,5m thì chịu được áp suất 2,85atm. Chọn B. Câu hỏi 8 : Cho hàm số y=(a−2)x+5 có đồ thị là đường thẳng d. Câu 1: Với giá trị nào của a thì hàm số trên đồng biến trên R.
Đáp án: A Phương pháp giải: Hàm số y=ax+b đồng biến trên R ⇔a>0 Lời giải chi tiết: Hàm số y=(a−2)x+5 là hàm số đồng biến trên R⇔a−2>0⇔a>2. Chọn A. Câu 2: Tìm a để đường thẳng d đi qua điểm M(2;3).
Đáp án: D Phương pháp giải: Điểm M(x0;y0) thuộc đường thẳng d:y=ax+b⇔y0=ax0+b Lời giải chi tiết: Thay x=2;y=3 vào hàm số y=(a−2)x+5 ta được 3=(a−2).2+5⇔2a−4+5=3⇔2a=2⇔a=1. Với a=1 thì đường thẳng d đi qua đểmM(2;3). Chọn D. Câu hỏi 9 : Số giá trị nguyên của m để hàm số y=(m2−9)x+3 nghịch biến là
Đáp án: A Phương pháp giải: Hàm số y=ax+b(a≠0) nghịch biến ⇔a<0. Lời giải chi tiết: Hàm số y=(m2−9)x+3 nghịch biến ⇔m2−9<0⇔−3<m<3. Lại có m∈Z⇒m∈{−2;−1;0;1;2}. Vậy có 5 giá trị nguyên của m thỏa mãn bài toán. Chọn A. Câu hỏi 10 : Cho hàm số y=f(x)=(1+m4)x+1, với m là tham số. Khẳng định nào sau đây đúng?
Đáp án: C Phương pháp giải: Hàm số y=ax+b(a≠0) đồng biến khi a>0 và nghịch biến khi a<0. Hàm số y=ax+b(a≠0) đồng biến ⇒∀x1>x2 ta có: f(x1)>f(x2). Hàm số y=ax+b(a≠0) nghịch biến ⇒∀x1>x2 ta có: f(x1)<f(x2). Lời giải chi tiết: Hàm số y=f(x)=(1+m4)x+1 có a=1+m4>0∀m⇒ hàm số đã cho đồng biến trên R. Khi đó chỉ có đáp án C đúng vì 2<3⇒f(2)<f(3). Chọn C. Câu hỏi 11 : Phương trình đường thẳng d có hệ số góc bằng 5 và đi qua điểm A(−1;1) là:
Đáp án: B Phương pháp giải: Gọi phương trình đường thẳng cần tìm theo công thức chung và theo những dữ kiện đã cho của bài để giải. Lời giải chi tiết: Gọi phương trình đường thẳng cần tìm có dạng: y=ax+b Theo bài ra có: a=5 và đi qua điểm A(−1;1) nên: 1=5.(−1)+b⇒b=6 Vậy phương trình cần tìm là y=5x+6. Chọn B Câu hỏi 12 : Biển Chết là hồ nước mặn nhất trên trái đất. Đây là nơi hoàn toàn bị bao bọc mà không có nước biển thoát ra ngoài. Điểm độc đáo của Biển Chết là sở hữu độ mặn cao gấp 9,6 lần so với nước biển thường. Đây là một trong những điểm du lịch độc đáo, du khách không bao giờ bị chìm và tận hưởng công dụng của muối biển đối với sức khỏe. (Biết rằng, nước biển thường có độ mặn là 3,5%) Thầy Tưởng lấy 500g nước Biển Chết và 400g nước biển thường rồi đổ chung vào một cái thùng. Sau đó, thầy cho thêm vào thùng 10 lít nước ngọt nữa. Hỏi nước trong thùng có thể là nước lợ được không? Biết nước lợ có độ mặn dao động từ 0,5%−1730%.
Đáp án: A Phương pháp giải: Bình luận về bài toán: Đây là một bài tập cơ bản của môn Hóa Học, để làm được bài tập này các em chỉ cần vận đụng công thức: C%=mctmdd..100⇒mct=mdd.C%100 Khối lượng chất tan (ở đây là muối) sau khi trộn lẫn bằng tổng khối lượng chất tan trong các dung dịch ban đầu. Khối lượng dung dịch sau khi trộn lẫn bằng tổng khối lượng của các dung dịch đem trộn + khối lượng nước thêm vào ( nếu có) 1 lít nước ngọt xem như có khối lượng = 1kg = 1000g Lời giải chi tiết: Nồng độ muối trong nước Biển Chết: 9,6. 3,5% = 33,6 % Khối lượng muối có trong 500g nước Biển Chết: m1=500.33,6100=168g Khối lượng muối có trong 400g nước biển thường: m1=400.3,5100=14g Khối lượng muối sau khi cho nước Biển Chết vào nước biển thường: m = m1 + m2 = 168 + 14 = 182g Nồng độ muối sau khi cho thêm vào thùng 10 lít nước ngọt: 182500+400+10000.100=1,67%>1730%⇒ nước trong thùng không phải là nước lợ. Câu hỏi 13 : Một anh công nhân dự định sau 9 năm sẽ mua được căn chung cư nhỏ trị giá 700 triệu đồng. Biết rằng, lương khởi điểm của anh công nhân đó là 5 triệu đồng/ tháng. Và cứ 3 năm, anh lại được sếp tăng lương thêm 7% vì anh làm việc rất chăm chỉ và hiệu suất cao. Hỏi sau 9 năm làm việc, anh công nhân có thể mua được căn chung cư như dự định không? Giả sử như toàn bộ tiền lương của anh dùng để mua nhà và không có bất cứ rủi ro nào khác xảy ra.
Đáp án: B Phương pháp giải: Lời giải chi tiết: Một năm có 12 tháng ⇒3 năm có 36 tháng. Mỗi tháng lương của anh là 5 triệu đồng ⇒trong 3 năm đầu tiên tổng tiền lương anh có là: T1=5.36=180 (triệu đồng) Trong 3 năm tiếp theo, anh được tăng lương thệm 7% nữa so với 3 năm đầu tiên, nên tổng số tiền anh có được trong 3 năm này là: T2=T1+7 (triệu đồng) Trong 3 năm tiếp theo, anh lại được tăng thêm 7% so với 3 năm trước, nên trong 3 năm này anh sẽ nhận được số tiền là: T3=T2+7(triệu đồng) Vậy tổng số tiền sau 9 năm anh công nhân nhận được là: T=T1+T2+T3=180+192,6+206,082=578,682(triệu đồng) < 700 triệu đồng. Như vậy, sau 9 năm anh công nhân chưa thể mua được căn chung cư mà anh mơ ước. Câu hỏi 14 : Năm nay số dân ở một thành phố A có 2 000 000 người. Hỏi 2 năm sau số dân của thành phố A là bao nhiêu người? Biết rằng bình quân mỗi năm số dân của thành phố A này tăng 0,5%.
Đáp án: D Phương pháp giải: Giả sử có số dân là P mỗi năm số dân tăng a , ta được số dân của năm đó tăng là P.a suy ra số dân sau một năm: P1=P+P.a%=P(1+a%) Chứng minh tương tự ta được sau n năm thì số dân là: Pn=P(1+a%)n Lời giải chi tiết: Cách 1: Áp dụng công thức trên ta có só dân của thành phố sau 2 năm là: P2=2000000.(1+0,5%)2=2020050 người Vậy sau 2 năm dân số của thành phố là 2020050 người. Cách 2: Dân số của thành phố A sau 1 năm là: 2000000+2000000.0,5 người. Dân số của thành phố A sau 2 năm là: 2010000+2010000.0,5 người. Vậy sau 2 năm dân số của thành phố là 2020050 người. Chọn D Câu hỏi 15 : Nhân ngày “Black Friday” (24/11/2017). Một cửa hàng điện tử thực hiện giảm giá 50% trên một tivi trong lô hàng gồm 40 cái tivi với giả bán lẻ ban đầu là 6.500.000 đ/cái. Đến trưa cùng ngày đã bán được 20 cái, khi đó cửa hàng quyết định giảm thêm 10% nữa trên giá đang bán cho mỗi tivi thì bán được hết lô hàng. Biết rằng giá vốn là 3.050.000 đ/một tivi. Hỏi cửa hàng đó lời hay lỗ khi bán hết lô tiền hàng tivi?
Đáp án: C Phương pháp giải: Muốn biết cửa hàng lời hay lỗ khi bán hết số tivi, ta so sánh số tiền nhập tivi về với số tiền thu được khi bán tivi. Nếu số tiền thu được lớn hơn số tiền nhập về thì là lời, nếu nhỏ hơn là lỗ.
Lời giải chi tiết: Sau khi giảm giá 50% thì giá một chiếc tivi là: 6500000.50%=3250000 đ Vì đến trưa cửa hàng bán được 20 cái tivi nên ta có số tiền thu được là:3250000.20=65000000đ Vì số tivi chưa bán hết nên cửa hàng quyết định giảm thêm 10% nữa trên giá đang bán cho mỗi tivi , giá bán sau đó của mỗi tivi là: 3250000.(100%−10%)=2925000 đ Vì sau khi giảm giá thì bán được hết 20 cái tivi còn lại nên số tiền thu về là: 2925000.20=58500000 đ Vậy tổng số tiền thu được khi bán hết tivi là: 65000000+58500000=123500000 đ Tổng số tiền nhập tivi là: 3050000.40=122000000 đ Xét hiệu: 123500000−122000000=1500000 đ Vì số tiền thu về lớn hơn số tiền nhập hàng nên cửa hàng đó lời khi bán hết 40 cái tivi với số tiền lời là 1500000 đ. Chọn C
|













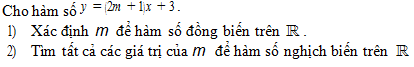
 -1/2; 2) m < -1/2
-1/2; 2) m < -1/2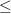 -1/2
-1/2