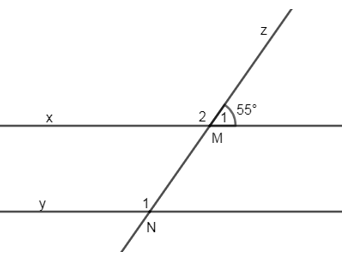
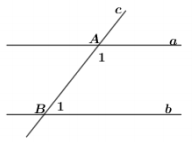
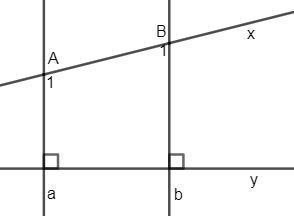
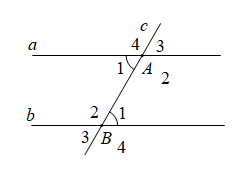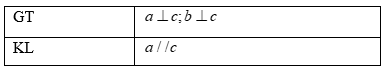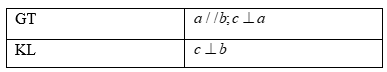20 bài tập vận dụng Từ vuông góc đến song songLàm bàiCâu hỏi 1 : Cho hình vẽ sau, biết \(x//y\) và \(\widehat{{{M}_{1}}}={{55}^{0}}\). Tính \(\widehat{{{N}_{1}}}\).
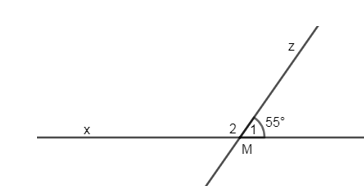
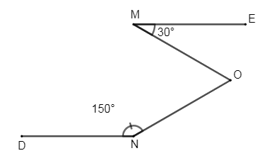
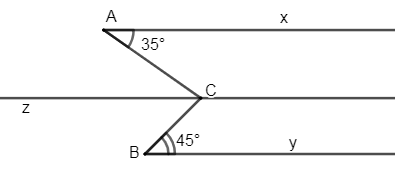
Đáp án: D Phương pháp giải: Áp dụng tính chất hai đường thẳng song song. Lời giải chi tiết: Ta có: \(\widehat{{{M}_{1}}}+\widehat{{{M}_{2}}}={{180}^{0}}\Rightarrow \widehat{{{M}_{2}}}={{180}^{0}}-{{55}^{0}}={{125}^{0}}\) (kề bù) Vì \(x//y\left( gt \right)\Rightarrow \widehat{{{M}_{2}}}=\widehat{{{N}_{1}}}={{125}^{0}}\) (2 góc đồng vị) Chọn D. Câu hỏi 2 : Cho hình vẽ sau Biết \(ME//N\text{D},\,\widehat{EM\text{O}}={{30}^{0}},\,\widehat{DNO}={{150}^{0}}\) . a) Tính \(\widehat{MON}\) . b) Tia OP có phải là phân giác của \(\widehat{MON}\) không? Vì sao?
Đáp án: A Phương pháp giải: Áp dụng tiên đề Ơ-clit, tính chất hai đường thẳng song song, dấu hiệu nhận biết tia phân giác. Lời giải chi tiết: a) Kẻ \(OP\) sao cho \(OP//ME.\) Ta có: \(OP//\,ME\Rightarrow \widehat{M}=\widehat{{{O}_{1}}}={{30}^{0}}\) (2 góc so le trong) Ta có: \(\left\{ \begin{align} & OP\,//\,ME \\& ME\,//\,DN \\\end{align} \right.\left( gt \right)\Rightarrow PO\,//\,DN\) \(\Rightarrow \widehat{{{O}_{2}}}+\widehat{N}={{180}^{0}}\) (2 góc trong cùng phía bù nhau) \(\Rightarrow \widehat{{{O}_{2}}}={{180}^{0}}-\widehat{N}={{180}^{0}}-{{150}^{0}}={{30}^{0}}\) Ta có: \(\widehat{MON}=\widehat{{{O}_{1}}}+\widehat{{{O}_{2}}}={{30}^{0}}+{{30}^{0}}={{60}^{0}}\) b) Vì tia OP nằm giữa hai tia OM và ON, lại có \(\widehat{{{O}_{1}}}=\widehat{{{O}_{2}}}\left( ={{30}^{0}} \right)\) Suy ra tia OP là phân giác của \(\widehat{MON}\). Chọn A Câu hỏi 3 : Cho hình vẽ sau: Biết \(c\bot a,\,\widehat{{{C}_{1}}}={{45}^{0}},\,\widehat{{{B}_{1}}}={{135}^{0}}\) . Chứng minh \(b\bot c\) . Phương pháp giải: Áp dụng tính chất: Hai đường thẳng song song, nếu đường thẳng thứ ba vuông góc với một trong hai đường thẳng đó thì nó vuông góc với đường thẳng còn lại. - Áp dụng dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết: Ta có: \(\widehat{{{B}_{1}}}+\widehat{{{B}_{2}}}={{180}^{0}}\) (kề bù) \(\begin{align} & \Rightarrow \widehat{{{B}_{2}}}={{180}^{0}}-\widehat{{{B}_{1}}}={{180}^{0}}-{{135}^{0}}={{45}^{0}} \\ & \Rightarrow \widehat{{{B}_{2}}}=\widehat{{{C}_{1}}}\left( ={{45}^{0}} \right) \\\end{align}\) Mà \(\widehat{{{B}_{2}}}\) và \(\widehat{{{C}_{1}}}\) là hai góc đồng vị nên suy ra \(a//\,b\)(dấu hiệu nhận biết hai đường thẳng song song) Lại có, \(c\bot a\left( gt \right)\Rightarrow b\bot c\) (quan hệ giữa tính vuông góc với tính song song) Câu hỏi 4 : Ở hình vẽ dưới đây, ta có \(\angle {A_1}\) và \(\angle {B_1}\) là cặp góc
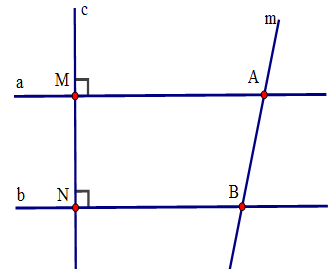
Đáp án: A Phương pháp giải: Căn cứ vào vị trí của góc so với hai đường thẳng và đường thẳng thứ ba mà ta xác định được vị trí của hai góc \(\angle {A_1}\) và \(\angle {B_1}\). Lời giải chi tiết: Trong hình vẽ bên ta thấy \(\angle {A_1}\) và \(\angle {B_1}\) là hai cặp góc trong cùng phía. Chọn A Câu hỏi 5 : Cho hai đường thẳng \(a\) và \(b\) cùng vuông góc với đường thẳng \(c,\) \(c\) vuông góc với \(a\) tại \(M\) và vuông góc với \(b\) tại \(N.\) Một đường thẳng \(m\) cắt \(a,b\) tại \(A,B.\) Biết \(\widehat {ABN} - \widehat {MAB} = 40^\circ \). Số đo góc \(BAM\) là:
Đáp án: B Phương pháp giải: + Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. + Tính chất hai đường thẳng song song. Lời giải chi tiết:
Từ đề bài ta có \(a \bot c;b \bot c \Rightarrow a//b\) (quan hệ từ vuông góc đến song song) Suy ra \(\widehat {ABN} + \widehat {MAB} = 180^\circ \) (hai góc trong cùng phía bù nhau) mà \(\widehat {ABN} - \widehat {MAB} = 40^\circ \) nên \(\widehat {ABN} = \frac{{180^\circ + 40^\circ }}{2} = 110^\circ \) và \(\widehat {MAB} = 180^\circ - \widehat {ABN} = 180^\circ - 110^\circ = 40^\circ \) Vậy \(\widehat {BAM} = 70^\circ .\) Chọn B. Câu hỏi 6 : Cho hình vẽ sau:
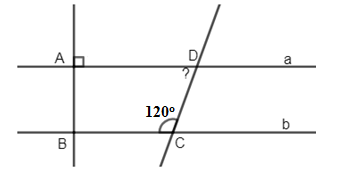
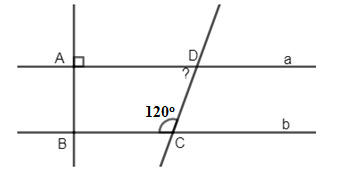
Biết \(a//\,b,\,\widehat {BC{\rm{D}}} = {100^0}\). Kết luận nào sau đây là đúng: .
Đáp án: D Phương pháp giải: + Áp dụng tính chất: Hai đường thẳng song song, nếu đường thẳng thứ ba vuông góc với một trong hai đường thẳng đó thì nó vuông góc với đường thẳng còn lại. + Tính chất hai đường thẳng song song. Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}a\,//\,b\\AB \bot a\end{array} \right. \Rightarrow AB \bot b\) (quan hệ giữa tính vuông góc với tính song song) Vì \(a//\,b\left( {gt} \right) \Rightarrow \widehat {A{\rm{D}}C} + \widehat {BC{\rm{D}}} = {180^0}\) (2 góc trong cùng phía bù nhau) \( \Rightarrow \widehat {A{\rm{D}}C} = {180^0} - \widehat {BC{\rm{D}}} = {180^0} - {120^0} = {60^0}\) Chọn D Câu hỏi 7 : Cho hình vẽ sau:
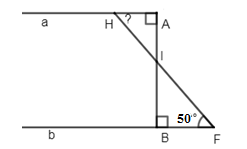
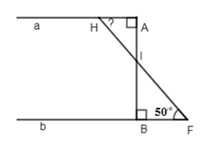
Biết \(AB \bot a,\,AB \bot b,\,\widehat {BFA} = {50^0}\). Tính \(\widehat {AHF}\).
Đáp án: C Phương pháp giải: + Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. + Tính chất hai đường thẳng song song. Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}AB \bot a\\AB \bot b\end{array} \right. \Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song) \( \Rightarrow \widehat {BFH} = \widehat {AHF} = {50^0}\) (so le trong) Chọn C Câu hỏi 8 : Cho hình vẽ sau:
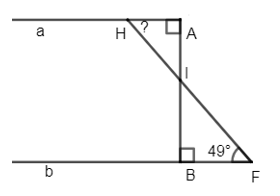
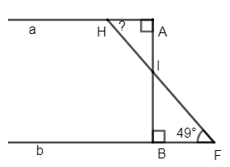
Biết \(AB\bot a,\,AB\bot b,\,\widehat{BFH}={{49}^{0}}\). Tính \(\widehat{AHF}\).
Đáp án: C Phương pháp giải: Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. - Tính chất hai đường thẳng song song. Lời giải chi tiết: Ta có: \(\left\{ \begin{align} & AB\bot a \\& AB\bot b \\\end{align} \right.\Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song) \(\Rightarrow \widehat{BFH}=\widehat{AHF}={{49}^{0}}\) (so le trong) Chọn C Câu hỏi 9 : Cho hình vẽ sau:
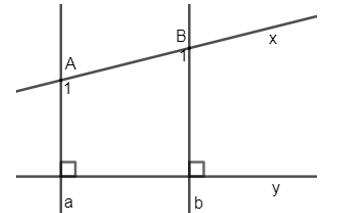
Biết \(a\bot y,\,b\bot y,\,\widehat{{{A}_{1}}}-\widehat{{{B}_{1}}}={{40}^{0}}\). Tính \(\widehat{{{B}_{1}}}\).
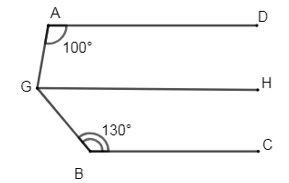
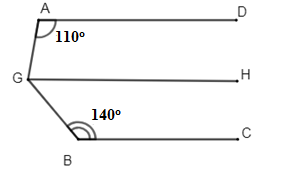
Đáp án: B Phương pháp giải: Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. - Tính chất hai đường thẳng song song. Lời giải chi tiết: Ta có: \(\left\{ \begin{align} & a\bot y \\& b\bot y \\\end{align} \right.\left( gt \right)\Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song) \(\Rightarrow \widehat{{{A}_{1}}}+\widehat{{{B}_{1}}}={{180}^{0}}\) (2 góc trong cùng phía bù nhau) Lại có: \(\widehat{{{A}_{1}}}-\widehat{{{B}_{1}}}={{40}^{0}}\left( gt \right)\Rightarrow \widehat{{{B}_{1}}}=\left( {{180}^{0}}-{{40}^{0}} \right):2={{70}^{0}}\) Chọn B. Câu hỏi 10 : Cho hình vẽ sau: Biết \(A\text{D}\,//\,GH,\,\,A\text{D}\,//\,BC,\,\widehat{DAG}={{100}^{0}},\,\widehat{GBC}={{130}^{0}}\). Tính \(\widehat{AGB}\).
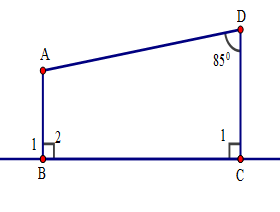
Đáp án: B Phương pháp giải: Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau. - Áp dụng tính chất hai đường thẳng song song. Lời giải chi tiết: Vì \(A\text{D}//\,GH\left( gt \right)\Rightarrow \widehat{GA\text{D}}+\widehat{AGH}={{180}^{0}}\Rightarrow \widehat{AGH}={{180}^{0}}-\widehat{GA\text{D}}={{180}^{0}}-{{100}^{0}}={{80}^{0}}\) (2 góc trong cùng phía bù nhau) Ta có: \(\left\{ \begin{align} & A\text{D}//\,GH \\ & A\text{D}//\,BC \\\end{align} \right.\left( gt \right)\Rightarrow GH//\,BC\) \(\Rightarrow \widehat{HGB}+\widehat{GBC}={{180}^{0}}\Rightarrow \widehat{HGB}={{180}^{0}}-\widehat{GBC}={{180}^{0}}-{{130}^{0}}={{50}^{0}}\) (2 góc trong cùng phía bù nhau) \(\widehat{AGB}=\widehat{AGH}+\widehat{HGB}={{80}^{0}}+{{50}^{0}}={{130}^{0}}\) Chọn B Câu hỏi 11 : Cho hình vẽ sau. Tính số đo góc \(BAD.\)
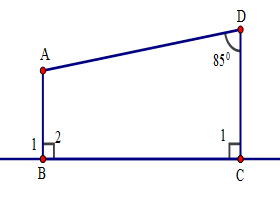
Đáp án: A Phương pháp giải: + Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. + Tính chất hai đường thẳng song song. Lời giải chi tiết:
Ta thấy \(AB \bot BC;DC \bot BC\) \( \Rightarrow AB//DC\) (quan hệ từ vuông góc đến song song) Suy ra \(\widehat {ADC} + \widehat {BAD} = 180^\circ \) (hai góc trong cùng phía bù nhau) \( \Rightarrow \widehat {BAD} = 180^\circ - \widehat {ADC} = 180^\circ - 85^\circ = 95^\circ \) Vậy \(\widehat {BAD} = 95^\circ .\) Chọn A. Câu hỏi 12 : Cho hình vẽ sau:
Biết \(a \bot y,\,b \bot y,\,\widehat {{A_1}} - \widehat {{B_1}} = {40^0}\). Tính \(\widehat {{B_1}}\).
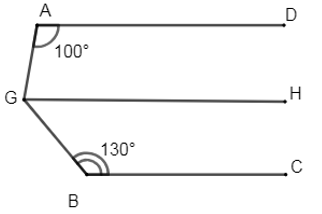
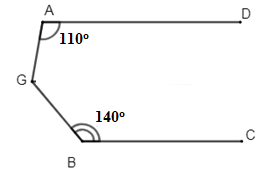
Đáp án: B Phương pháp giải: + Áp dụng tính chất: Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. + Tính chất hai đường thẳng song song. Lời giải chi tiết: Ta có: \(\left\{ \begin{array}{l}a \bot y\\b \bot y\end{array} \right.\left( {gt} \right) \Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song) \( \Rightarrow \widehat {{A_1}} + \widehat {{B_1}} = {180^0}\) (2 góc trong cùng phía bù nhau) Lại có: \(\widehat {{A_1}} - \widehat {{B_1}} = {40^0}\left( {gt} \right) \Rightarrow \widehat {{B_1}} = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}\) Chọn B. Câu hỏi 13 : Cho hình vẽ sau biết \(AD//BC.\) Tính \(\widehat {AGB}.\)
Đáp án: A Phương pháp giải: + Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau. + Áp dụng tính chất hai đường thẳng song song. Lời giải chi tiết:
Qua \(G\) kẻ \(GH//AD.\) Vì \(A{\rm{D}}//\,GH \Rightarrow \widehat {GA{\rm{D}}} + \widehat {AGH} = {180^0} \Rightarrow \widehat {AGH} = {180^0} - \widehat {GA{\rm{D}}} = {180^0} - {110^0} = {70^0}\) (2 góc trong cùng phía bù nhau) Ta có: \(\left\{ \begin{array}{l}A{\rm{D}}//\,GH\\A{\rm{D}}//\,BC\end{array} \right.\left( {gt} \right) \Rightarrow GH//\,BC\) \( \Rightarrow \widehat {HGB} + \widehat {GBC} = {180^0} \Rightarrow \widehat {HGB} = {180^0} - \widehat {GBC} = {180^0} - {140^0} = {40^0}\) (2 góc trong cùng phía bù nhau) \(\widehat {AGB} = \widehat {AGH} + \widehat {HGB} = {70^0} + {40^0} = {110^0}\) Chọn A. Câu hỏi 14 : Cho hình vẽ sau:
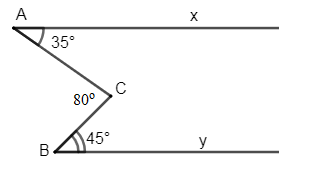
Biết \(\widehat {xAC} = {35^0},\,\widehat {CBy} = {45^0}\) và \(\widehat {ACB} = {80^0}.\) Khi đó chọn câu đúng.
Đáp án: B Phương pháp giải: + Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau. + Dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết:
Kẻ \(Cz//{\rm{Ax}} \Rightarrow \widehat {xAC} = \widehat {ACz} = {35^0}\) (so le trong) Ta có: \(\widehat {ACz} + \widehat {zCB} = \widehat {ACB} \Rightarrow \widehat {zCB} = \widehat {ACB} - \widehat {ACz} = {80^0} - {35^0} = {45^0}\) \( \Rightarrow \widehat {zCB} = \widehat {CBy}\left( { = {{45}^0}} \right)\) Mà hai góc ở vị trí so le trong nên suy ra \(Cz//\,By\) (dấu hiệu nhận biết hai đường thẳng song song) Ta có: \(\left\{ \begin{array}{l}Cz//\,Ax\left( {gt} \right)\\C{\rm{z}}//\,By\left( {cmt} \right)\end{array} \right. \Rightarrow Ax//\,By\) . Chọn B. Câu hỏi 15 : Cho hình vẽ sau:
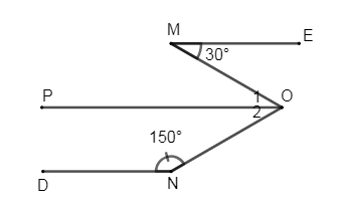
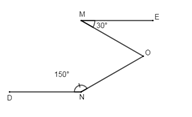
Biết \(ME//N{\rm{D}},\,\widehat {EM{\rm{O}}} = {30^0},\,\widehat {DNO} = {150^0}\). Tính \(\widehat {MON}\) .
Đáp án: C Phương pháp giải: Áp dụng tiên đề Ơ-clit, tính chất hai đường thẳng song song, dấu hiệu nhận biết tia phân giác. Lời giải chi tiết:
Kẻ \(OP\) sao cho \(OP//ME.\) Ta có: \(OP//\,ME \Rightarrow \widehat M = \widehat {{O_1}} = {30^0}\) (2 góc so le trong) Ta có: \(\left\{ \begin{array}{l}OP\,//\,ME\\ME\,//\,DN\end{array} \right.\left( {gt} \right) \Rightarrow PO\,//\,DN\) \( \Rightarrow \widehat {{O_2}} + \widehat N = {180^0}\) (2 góc trong cùng phía bù nhau) \( \Rightarrow \widehat {{O_2}} = {180^0} - \widehat N = {180^0} - {150^0} = {30^0}\) Ta có: \(\widehat {MON} = \widehat {{O_1}} + \widehat {{O_2}} = {30^0} + {30^0} = {60^0}\) Vậy \(\widehat {MON} = 60^\circ .\) Chọn C. Câu hỏi 16 : Phần giả thiết: \(c \cap a = \left\{ A \right\};c \cap b = \left\{ B \right\}\), \(\widehat {{A_1}} + \widehat {{B_2}} = 180^\circ \) (tham khảo hình vẽ) là của định lý nào dưới đây?
Đáp án: D Phương pháp giải: Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết: Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song. Chọn D. Câu hỏi 17 : Phát biểu định lý sau bằng lời:
Đáp án: C Phương pháp giải: Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra Lời giải chi tiết: Định lý: Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau. Chọn C. Câu hỏi 18 : Định lý sau được phát biểu thành lời là:
Đáp án: A Phương pháp giải: Giả thiết của định lí là điều cho biết. Kết luận của định lí là điều được suy ra. Lời giải chi tiết: Định lý: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia. Chọn A. Câu hỏi 19 : Cho hình vẽ sau:
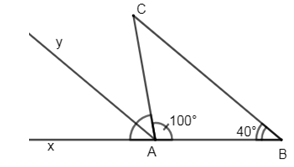
Biết \(\widehat{xAC}={{35}^{0}},\,\widehat{CBy}={{45}^{0}}\) và \(\widehat{ACB}={{80}^{0}}.\) Chứng minh \(Ax\,//\,By\). Phương pháp giải: Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau. - Dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết: Kẻ \(Cz//\text{Ax}\Rightarrow \widehat{xAC}=\widehat{ACz}={{35}^{0}}\) (so le trong) Ta có: \(\begin{align} & \widehat{ACz}+\widehat{zCB}=\widehat{ACB}\Rightarrow \widehat{zCB}=\widehat{ACB}-\widehat{ACz}={{80}^{0}}-{{35}^{0}}={{45}^{0}} \\ & \Rightarrow \widehat{zCB}=\widehat{CBy}\left( ={{45}^{0}} \right) \\\end{align}\) Mà hai góc ở vị trí so le trong nên suy ra \(Cz//\,By\) (dấu hiệu nhận biết hai đường thẳng song song) Ta có: \(\left\{ \begin{align} & Cz//\,Ax\left( gt \right) \\ & C\text{z}//\,By\left( cmt \right) \\\end{align} \right.\Rightarrow Ax//\,By\) . Câu hỏi 20 : Cho \(\Delta ABC\) có \(\widehat{A}={{100}^{0}},\,\widehat{B}={{40}^{0}}\) . Vẽ Ax là tia đối của tia AB rồi vẽ tia Ay là tia phân giác của \(\widehat{CAx}\) Hỏi Ay có song song với BC hay không? Vì sao? Phương pháp giải: Áp dụng tính chất tia phân giác của một góc, dấu hiệu nhận biết hai đường thẳng song song. Lời giải chi tiết: Vì Ax và AB là hai tia đối nhau nên ta có: \(\widehat{xAC}+\widehat{CAB}={{180}^{0}}\Rightarrow \widehat{xAC}={{180}^{0}}-\widehat{CAB}={{180}^{0}}-{{100}^{0}}={{80}^{0}}\) Vì tia Ay là phân giác của \(\widehat{xAC}\left( gt \right)\Rightarrow \widehat{xAy}=\widehat{xAC}:2={{80}^{0}}:2={{40}^{0}}\Rightarrow \widehat{xAy}=\widehat{ABC}\left( ={{40}^{0}} \right)\) Mà hai góc đó ở vị trí đồng vị nên suy ra \(Ay//\,BC.\)
|